神经网络学习笔记(二)——循环神经网络RNN

循环神经网络 RNN

一、概述

  循环神经网络（Recurrent neural network，RNN）是一类以序列（sequence）数据为输入，在序列的演进方向进行递归（recursion）且所有节点（循环单元）按链式连接的递归神经网络。
  时间循环神经网络可以描述动态时间行为，RNN将状态在自身网络中循环传递，因此可以接受更广泛的时间序列结构输入。循环神经网络具有记忆性、参数共享并且图灵完备（Turing completeness），因此在对序列的非线性特征进行学习时具有一定优势 。手写识别是最早成功利用RNN的研究结果。

二、背景

  传统神经网络只能单独的取处理一个个的输入，前一个输入和后一个输入是完全没有关系的。但是，某些任务需要能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。

比如，在理解一句话意思时，孤立的理解这句话的每个词是不够的，而需要处理这些词连接起来的整个序列； 处理视频的时候，也不能只单独的去分析每一帧，而要分析这些帧连接起来的整个序列。

  所以为了能够更好的处理序列的信息，RNN就诞生了。

三、RNN原理

3.1 模型结构

  基础的神经网络只在层与层之间建立了权连接，RNN最大的不同之处就是在层之间的神经元之间也建立的权连接。常规的RNN模型结构如下：

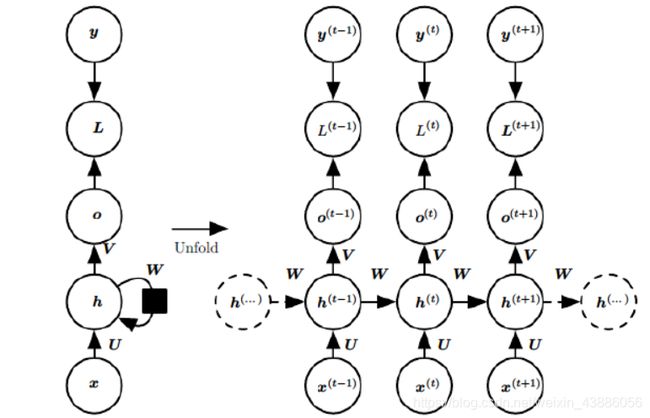
  右侧为左侧模型按照时间序列展开之后的模型。

• $x^{(t)}$为在序列索引号t时训练样本的输入；
• $h^{(t)}$为在序列索引号t时模型的隐藏状态，由$x^{(t)}$和$h^{(t-1)}$共同决定；
• $o^{(t)}$为在序列索引号t时模型的输出，由模型当前的隐藏状态$h^{(t)}$决定；
• $L^{(t)}$为在序列索引号t时模型的损失函数；
• $y^{(t)}$为在序列索引号t时训练样本序列的真实输出；
• $U$是输入层到隐藏层的权重矩阵；
• $V$是隐藏层到输出层的权重矩阵；
• $W$是隐藏层上一次的值作为这一次的输入的权重。

  用公式表达为如下形式：
$$\{\begin{array}{l}{o}^{(t)}=g(V\cdot h^{(t)})\\ h^{(t)}=f(U\cdot x^{(t)}+W\cdot h^{(t-1)})\end{array}$$

3.2 前向传播

  对于任意一个序列索引号$t$，隐藏状态$h^{(t)}$由$x^{(t)}$和$h^{(t-1)}$得到：
$$h^{(t)}=\sigma (z^{(t)})=\sigma (U{x}^{(t)}+W{h}^{(t-1)}+b)$$
  其中$\sigma$为激活函数，一般为$\tanh$，$b$为线性偏置。
  序列索引号$t$时模型的输出$o^{(t)}$为：
$$o^{(t)}=V{h}^{(t)}+c$$
  在序列索引号$t$时预测输出为:
$$y^{(t)}=\sigma (o^{(t)})$$
  其中$\sigma$为激活函数，通常RNN用于分类，因此一般用softmax函数$g(z_i)=\frac{e^{z_i}}{{\sum }_k{e}^{z_k}}$。

3.3 反向传播BPTT(back-propagation through time)

  BPTT算法是针对循环层的训练算法，它的基本原理和BP算法一样的：

• 前向计算每个神经元的输出值；
• 反向计算每个神经元的误差项；
• 计算每个权重的梯度
• 用随机梯度下降算法更新权重

  在RNN模型中，需要寻优的参数有三个，分别是U、V、W。其中W和U需要追溯之前的历史数据，而V只需关注目前。由于我序列的每个位置都有损失函数，因此最终的损失L为：
$$L=\sum _{t=1}^{\tau }{L}^{(t)}$$

  先求对$V$的梯度：
$$\frac{\partial L}{\partial V}=\sum _{t=1}^{\tau }\frac{\partial L^{(t)}}{\partial V}=\sum _{t=1}^{\tau }(y^{(t)}-y^{(t)})(h^{(t)}{)}^T$$

  再求$L$对$W,U$的梯度：
$$\frac{\partial L^{(t)}}{\partial W}=\sum _{t=0}^{\tau }[\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}(\prod _{j=t+1}^{\tau }\frac{\partial h^{(j)}}{\partial h^{(j-1)}})\frac{\partial h^{(t)}}{\partial W}]$$
$$\frac{\partial L^{(t)}}{\partial U}=\sum _{t=0}^{\tau }[\frac{\partial L^{(t)}}{\partial o^{(t)}}\frac{\partial o^{(t)}}{\partial h^{(t)}}(\prod _{j=t+1}^{\tau }\frac{\partial h^{(j)}}{\partial h^{(j-1)}})\frac{\partial h^{(t)}}{\partial U}]$$

  查看中间的累乘部分，
$$\prod _{j=t+1}^{\tau }\frac{\partial h^{(j)}}{\partial h^{(j-1)}}=\prod _{j=t+1}^{\tau }{\sigma }^{\prime }\cdot W_s$$
  而$\sigma (x)$为$sigmoid$或者$tanh$时，容易导致梯度消失，所以此处的激活函数常用ReLU函数，$ReLU(x)=\max (x,0)$。

3.4 RNN的分类

  对于RNN来说，根据不同的问题需要不同的输入输出结构（输入$T_x$，输出$T_y$）。按照$T_x$与$T_y$的关系，RNN模型包含以下几个类型：

• Many to many：$T_x=T_y$，输入和输出的长度相同，常用于人名识别，实体识别；
• Many to many：$T_x\ne T_y$，输入和输出都是序列，但长度却不相同，多见于机器翻译；
• Many to one：$T_x>1,T_y=1$，用作对某个序列进行正负判别或者打星操作，如文本分类，情感分类；
• One to many：$T_x=1,T_y>1$，应用有语音生成，文本生成；
  One to one：$T_x=1,T_y=1$，用的不多。
  

3.5 RNN的改进

双向RNN

  不仅可以依赖前面的上下文，还可以依赖后面的上下文。

深度RNN

  不仅在隐藏层有前后序列的关系，网络的其它层次也可以具有序列关系。

四、RNN的简单使用

  在自然语言处理中，上下文关系对模型有着较大的影响，而RNN比传统的神经网络模型能更好的处理这种关系。将每个单词作为一个特征向量，利用nn.RNN模型对语料进行了文本分类的处理。

  首先从文件中读取相应训练集和测试集的语料，利用jieba对文本进行分词，然后利用nltk去停用词。这里nltk_data中并没有中文的停用词，我从网上找了一个中文的停用词文件放在对应的stopwords目录下，并命名为chinese。

def tokenizer(text):
    sentence = jieba.lcut(text, cut_all=False)
    stopwords = stopwords.words('chinese')
    sentence = [_ for _ in sentence if _ not in stopwords]
    return sentence

  利用torchtext包处理预处理好的语料，将所提供的语料集转化为相应的词向量模型。由于每一个词均为一个向量，，作为RNN的输入。

train_set, validation_set = data.TabularDataset.splits(
            path='corpus_data/',
            skip_header=True,
            train='corpus_train.csv',
            validation='validation.csv',
            format='csv',
            fields=[('label', label), ('text', text)],
        )
text.build_vocab(train_set, validation_set)

  将处理好的词向量输入到RNN模型中进行处理。

self.rnn = nn.RNN(embedding_dim, self.hidden_size, batch_first=True, nonlinearity="relu")
self.linear = nn.Linear(self.hidden_size, label_num)
def forward(self, x):
    # 输入x的维度为(batch_size, max_len),
    x = self.embedding(x)  # 经过embedding,x的维度为(batch_size, time_step, embedding_dim)

    # 隐层初始化
    # h0维度为(direction_num, batch_size, hidden_size)
    h0 = torch.rand(1, x.size(0), self.hidden_size)
    # out维度为(batch_size, seq_length, hidden_size*direction_num)
    out, hn = self.rnn(x, h0)
    # 只需要最后一步的输出状态
    out = out[:, -1, :]
    out = self.linear(out)
    return out

  利用训练集对模型进行训练，同时评估训练效果，并利用测试集对模型的准确性进行评估。为了防止偶然性产生的不确定，每一轮迭代会产生100个模型，分别评估其效率，进行调优后再用测试集测试其效率。

  在训练初期，准确率大概在45%左右。

  多轮迭代之后，模型的准确率可以达到90%以上。

五、总结

• 优点

  • 适合处理序列问题，输入数据的判别和预测与相邻数据有关
  • 在序列问题中对短期记忆型的任务的效果更好
  • 可以和CNN一起使用得到更好的任务效果

• 不足

  • 梯度消失、梯度爆炸的问题
  • rnn较其他cnn和全连接要用更多的显存空间，更难训练
  • 如果采用tanh、relu为激活函数，没法处理太长的序列
  • 如果需要实现长期记忆的话需要将当前的隐含态的计算与前n次的计算挂钩，计算量会呈指数式增长

• RNN 几个典型的应用如下：

  • 语言模型与文本生成
  • 语音识别
  • 机器翻译
  • 生成图像描述
  • 视频标记