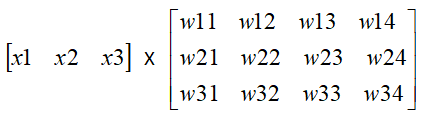管中窥豹--机器学习之我见
人工智能领域显然是这两年技术的热点区域,特别是机器学习、深度学习、各种神经网络技术,更是火的一塌糊涂。
这些技术都被冠以智能的高帽,让人望而生畏。不过,我突然发现一个有意思的现象。当你对一个三、四岁的小孩提问时,他会思考一下,然后要么告诉你他的理解,要么回答你不知道。可是,如果提问的对象是各种所谓智能的语音助手的话,这些“智者”很难回答你一句不知道,而是想方设法,总会回答你点什么,即使风马牛不相及。如果真有那么一天,智能机器人被创造出来的话,我觉得他们一定是非常外向的。
下面梳理下我对机器学习的粗浅理解。
首先,确定要解决的问题。
其次,研究问题涉及的方面。
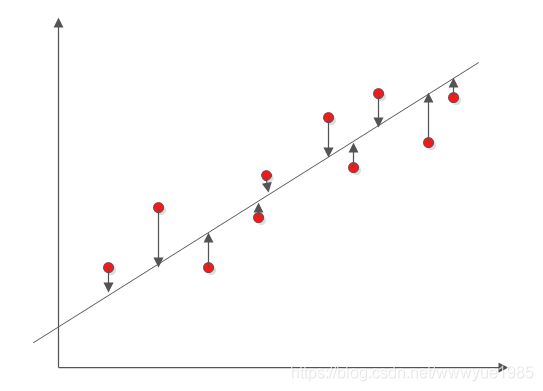
最后,选择一个模型。比如线性回归模型,最简单的情况如一条直线,y=kx+b。复杂的,Y=AX+W,变成矩阵形式,对应张量。
以上为第一部分。针对问题域,确定大的算法范围,也可以理解为建一个好的模型。有了模型后,需要继续明确以下元素。
一 确定成本函数(评估函数 损失函数 评价函数...)。不管是哪种叫法,目的都是评价当前结果的优劣,为下一步的行动提供参考。比如最简单的,使用均方误差,复杂的,各种距离,范数等。
上图就是基于均方误差评估线性模型。
二 确定梯度下降算法。梯度下降,我理解是最快接近目标的方向。假设成本函数越小越好,则梯度下降方向意味着选择成本函数下降最快的参数,从而能够最快到达期望的极值。当然,这里存在局部极值和全局极值,正常是要找到全局极值。
三 确定学习率。还没有理解数学含义。不过通过查阅网上的一些资料了解到这个参数是一个经验值,需要多次试验后才可能取得较好的训练效果。个人理解,对于梯度下降,学习率会影响到每次探测的距离。当这个值比较小时,探测的就比较精细,不容易错过极值,但是明显的,需要耗费更多的时间;如果这个值比较大时,探测的就会比较粗糙,容易错过极值,甚至无法找到极值,难以收敛,好处就是速度快。
四 训练模型。模型只是一个抽象的指导思想、机制、方法论,至于具体的策略、判断逻辑是什么样子,还需要通过训练来获取。所谓训练,就是把获取的样本数据,输入到模型框架中,从而不断的对模型进行修正,明确化,使得其对样本的预测极限接近真实结果。
比如就上面的线性模型而言,选择直线模型,而非曲线或其他形状,这只是一个策略预判。在不同的样本空间中,这个直线的倾斜角度怎样,这就是需要训练明确的。一旦训练完成,直线的样子也就明确化了,而不再是一个抽象的、笼统的直线概念。
为了更好的控制训练过程,会有一些参数,比如epoch, iteration, batch_size等。具体含义可百度查看。
五 确定结束条件。训练过程是一个循环优化的过程。这个过程得有个结束条件,要么是达到了预期的精度或阈值,要么是达到了设定的循环次数。
以上为第二部分。针对模型,使用样本数据进行训练,获取针对该问题域使用该模型的最优参数。有了训练好的模型,下一步就是让其发挥功效,这就是预测了。这也是前面所有工作的目的。
六 预测。有了训练得到的具体化、参数化的模型,就可以用其来进行预测了。所谓预测,就是将新的数据条件输入模型,由模型给出结果、判断或者分类等。比如对上述线性模型,
输入新的“x”条件,即可得到近似的“y”结果。
通过上面的梳理,我们来看所谓的机器学习、深度学习,以及进一步的深度神经网络等等,本质上是什么?是真的智能吗?显然,从上面的线性回归例子,还丝毫看不出智能的影子。
那这些所谓的学习到底在学习什么?怎么学习?从目前来看,大部分的学习都需要大量的样本数据,整个学习过程弥漫着获取统计特性的味道。神经网络也并非跟人类大脑里的神经网络是一回事,而是类似神经网络的一种模型结构。总的来看,个人理解,所谓的学习,本质上就是构造一种拟合数据的过滤器。特别是有监督类的学习。学习过程就是不断的用已知数据加上人类已知的一些策略对过滤器调优,直到达到预先设定的条件为止。上面的线性回归就是最简单的拟合过滤器,一条直线。复杂点的有曲线,曲面,以及更复杂的无明显可视规则的高维空间“形状”。举个不那么恰当的例子,某个神经网络结构最终构造出来的拟合过滤器也许是下面这个纸团样子,新数据通过它得到预测结果。
提到神经网络,补充记录一点。之前参加一个活动,在介绍神经网络底层硬件优化时提到神经网络的底层本质是矩阵计算,所谓的优化就是如何提升矩阵计算的性能。活动结束后,中间的种种一概不再记得,唯有这个“神经网络的底层本质是矩阵计算”一直萦绕在脑海中,挥之不去。突然一个早晨,灵光一闪,想明白了,特此记录在这里。
虽然很简单,但是对于久不接触数学的俺来讲,还是有那么一点小小的成就感。
以下图为例,左边为输入,中间为隐层,右边为输出。
对输入到隐层的连接,进行编号。比如x1引出到1的权重为W11,到2的权重为W12,x2引出到1的权重为w21,到2的权重为w22,...以此类推。则有:
节点1的结果为 x1*w11+x2*w21+x3*w31
节点2的结果为 x1*w12+x2*w22+x3*w32
节点3的结果为 x1*w13+x2*w23+x3*w33
节点4的结果为 x1*w14+x2*w24+x3*w34
这不就是下面矩阵的乘吗!