动态规划 | 可以用在核酸检测的算法：莱文斯坦算法

核酸检测经此一疫已经成为了人尽皆知的检测手段，但是你可曾想过经过仪器检测出来的 DNA序列是如何与正常情况下的 DNA 序列做对比的呢？面对整村的核酸检测结果，计算工作肯定需要电脑来完成，如果我们想知道一个受试者的 DNA 序列与正常情况下的 DNA 序列有至少几个个元素差异时，我们就需要一个算法来解决，它叫 莱文斯坦 (levenshtein) 算法，而这个算法背后有一个主要的技术：动态规划！

import numpy as np

本文将只通过 numpy 从头构建莱文斯坦算法，如果还没安装这个库的读者们可以通过下面指令在终端安装：

pip install numpy

编辑距离

DNA 序列主要可以用四种英文字母表示，ATCG，至于什么样的检测结果要对应到什么样的英文字母不在这篇文章的讨论范围，我们只讨论如何处理这些序列数据。假如检测站的样本里我们的到了两组 DNA 序列：

判断这两组序列与目标序列之间的差异前，我们需要先定义差异的含义，也就是编辑距离，面对一个序列，我们需要经过几步操作才能够使其和目标序列变得一模一样，如果是三步，那么编辑距离就是3。但是广义地说，修改一个序列使其和另一个序列一样的方法有无限多种，因此我们需要给另一个约束条件，就是如何用最少的步骤来完成修改的操作，而具体操作动作只能包含下面三种方式：

1. 插入
2. 删除
3. 替换

为了有效解决这个问题，动态规划就是本篇文章所介绍算法的核心逻辑！

动态规划

动态规划的核心概念就是把一个大的问题拆分成很多个小的问题分别击破，使得整体问题难度降低，进而更容易找出问题的最优答案。面对 DNA 序列问题，大问题就是一串完整的序列到底有哪些不同，而小问题则是对应到每个位置上的字符，到底是应该采取什么样的动作，先给出计算两个不同序列编辑距离的计算过程。

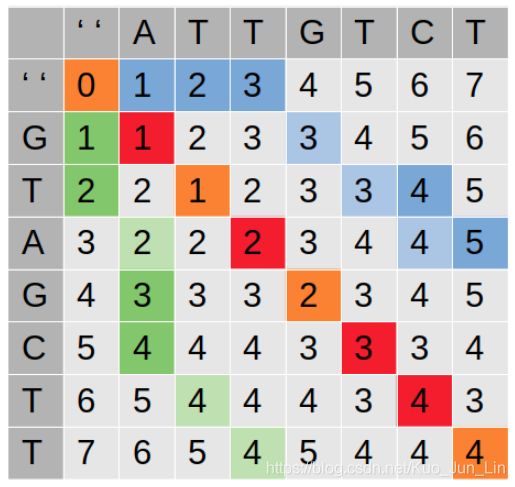
为了把 “ATTGTCT” 改成 “GTAGCTT”，根据矩阵里最右下角的计算结果，最少的操作步骤就是 4 步，至于这四个步骤具体是 插入，删除，替换 怎么样的排列组合，那得依据计算矩阵右下角数字的过程中小编所标注的框的颜色和对应到一个 2x2 的行为矩阵来判定：

如果我们把行为矩阵里的右下角位置对应到大矩阵里每一个红色框，红框的数字全是从大矩阵中橙色框 + 1 而得到的，而橙色框对应了行为矩阵则是 替换 的操作！通过同样的规律，我们也可以从蓝色的路径了解到从 “ATTGTCT” 变到 “GTA” 最少需要 5 步，从 “ATT” 变到 “GTAGCTT” 则需要 4 步，至于具体填上数字的细节，小编马上接着说！

1. 原理细节

在最一开始什么数字都不存在在矩阵中时，只有 变化前 的序列被放在最上面，和 变化后 的序列被放在最左边，而序列的最前面需要填上一个代表本来什么都没有的站位符，我们可以理解为一个字符串在最易开始是什么元素都没有的，因此不论是变化前后两个序列最前面都得加上空的占位符。接着，我们就能开始逐一解大问题中的每一个小问题，从空的占位符变成任意长度的序列所需要的步数肯定等于序列的长度，因此第一个行列就可以理所当然的填上 0 1 2 … 7。

剩下来还没填上数字的格子，我们就需要以 2x2 所排部的四个格子为单位去计算最小的步骤，而这四个格子也就刚好对应了行为矩阵的位置，为了确定小问题的最优操作，我们需要知道分别操作了 插入，删除，替换 之后，最小的成本是多少。

1-1. 不同元素 - 绿色方形块

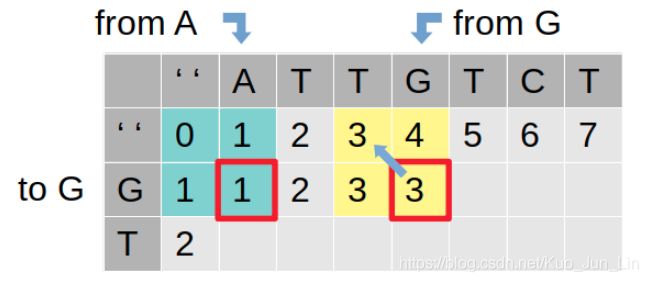
如果对应位置的字母需要被改变，例如图中 A 要换成 G，至少 1 步 (替换) 需要操作，但这是因为一开始问题一目了然，能够通过直觉看出问题的解，实际上在动态规划的思维中，我们需要发现一个能够一直被重复使用的规律，因此 A 换成 G 是 1 步的答案背后应该要根据 2x2 范围里的数字去比较：

• 0 + 1 表示替换 A 成 G 所需要的步数
• 1 + 1 表示插入 A 成 G 所需要的步数
• 1 + 1 表示删除 A 成 G 所需要的步数

而最后根据这三个操作的结果来看，证明了最少步数是替换操作，因此这步将遵循此操作，并把 0 + 1 的结果写进 2x2 矩阵范围的右下角。

1-2. 相同元素 - 黄色方形块

相反地，如果我们遇到要把 G 换成 G 的情况，就直接把 2x2 矩阵范围的左上角数字抄到右下角，因为同样的字符是不需要做任何变动的，也就没有任何一个操作合适，所以最少步数的结论就还是 3 步。了解了处理 不同元素 与 相同元素 的计算规则之后，就可以逐一填上矩阵里每一个位置对应的数字，有时候在某几个特殊的环节我们可能会发现对序列的最少步骤操作可能不是唯一的，这其实是可以接受的，只要两个不唯一的系列操作最终都是同样的步骤数量就行，很明显的例子就是上图中大矩阵的蓝色路径，最后的部分，其实先删除在取代，或者先取代再删除其实都能达到同样的效果，虽然序列操作最后有点不同，但都还是得花 5 步来完成序列的修改。

---

觉得有收获的话，欢迎关注、转发、分享！AI 算法辞典 公众号同步更新，扫码关注！

---

2. 动态规划代码

根据上面所解释的逻辑，我们需要在迭代过程中不断寻找 2x2 区域里面的最少步长，如果发现当前的转换前转换后字符是一样的，那就直接拷贝 2x2 区域里面的左上角值接着迭代：

def Levenshtein(astr, bstr):
    # 读取输入的两个字符串并创建一个空的矩阵
    rows, cols = (len(bstr) + 1, len(astr) + 1)
    matrix = np.array([None] * (rows*cols)).reshape(rows, cols)
    
    # 加上第一行与第一列的初始值
    matrix[0, :] = np.arange(cols)
    matrix[:, 0] = np.arange(rows)
    
    # 对序列中的所有字符逐一遍历
    for i, b in enumerate(bstr):
        for j, a in enumerate(astr):
            # 如果两个字符是一样的, ...
            if a == b:
                # ... 直接拷贝左上角的值
                matrix[i+1, j+1] = matrix[i, j]
            else:
                # 否则就找 2x2 矩阵中最少步长
                matrix[i+1, j+1] = np.min([matrix[i+0, j+1],
                                           matrix[i+0, j+0],
                                           matrix[i+1, j+0]]) + 1
    return matrix


print(Levenshtein('ATTGTCT', 'GTAGCTT'))

输出:
[[0, 1, 2, 3, 4, 5, 6, 7],
 [1, 1, 2, 3, 3, 4, 5, 6],
 [2, 2, 1, 2, 3, 3, 4, 5],
 [3, 2, 2, 2, 3, 4, 4, 5],
 [4, 3, 3, 3, 2, 3, 4, 5],
 [5, 4, 4, 4, 3, 3, 3, 4],
 [6, 5, 4, 4, 4, 3, 4, 3],
 [7, 6, 5, 4, 5, 4, 4, 4]]

其他类似的序列替换问题同样可以通过这个简单的动态规划算法来计算出两个序列之间的 编辑距离，例如我们可以把本来用来装 DNA 信息的颜色框拿去装一个单词，这么一来我们就能分析两句話之间有几个单词不一样。总的来说，莱文斯坦算法是一个非常轻巧但同时在自然语言处理领域非常好用的一个算法！值得一试！