FCOS论文笔记
论文:FCOS: Fully Convolutional One-Stage Object Detection
论文链接:https://arxiv.org/abs/1904.01355
论文代码:https://github.com/tianzhi0549/FCOS
Introduction
首先作者按照“惯例”说明了基于Anchor based
检测器的缺点:
- 基于Anchor的检测算法,检测效果受预选框尺寸和比例大小、以及检测框数量的影响很大
- Anchor的设置,如尺寸、比例固定,导致基于Anchor的检测算法在处理尺度变化大或者小目标的时候存在一些问题
- 基于Anchor的检测算法,会导致正负样本不平衡
- 在训练过程中,还需要候选框与GroundTruth的IoU这样复杂的计算过程。
鉴于全卷积神经网络的dense prediction在分割、关键点检测等领域取得的成就,作者尝试讲全卷积神经网络运用到检测当中,对每个pixel进行预测。此前也不是没有通过对每个pixel进行密集预测的检测器(DenseBox、YOLOv1),但都存在不少的问题。对于DenseBox,它必须讲候选框裁剪到固定的尺寸,才能输入到网络中。因此其必须使用图像金字塔进行训练。而对于YOLOv1由于是对每个pixel预测两个候选框,其预测结果会严重遗漏候选框。在对pixel进行密集预测中,有一个问题必须要解决,即对于高度重合的候选框,同一个像素点要回归到哪一个候选框是难以节点的。比如图一中右图,对于同一个像素点,是回归到橙色框还是蓝色框,是pixel密集预测需要解决的问题
Method
Architecture
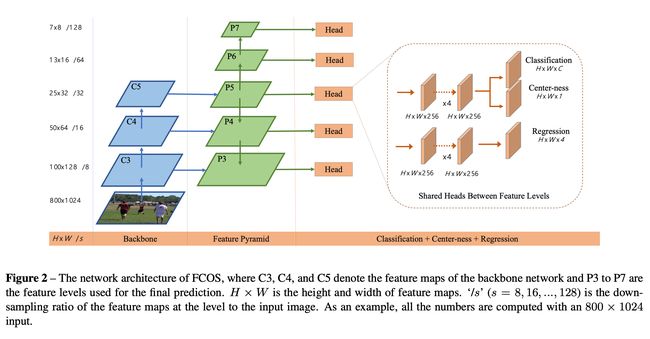
FCOS的整体框架图如上图所示,同样的与FoveaBox一样,是在RetinaNet的架构上作修改。和FoveaBox一样将RetinaNet的输出的两个feature map的channel做了修改,输出的用于分类feature map通道数从C * A改成了C[C表示数据集的类别数,A表示RetinaNet设置的anchor数量],而用于回归的feature map通道数则是从4 * A改成了4,完全摒弃了Anchor。其思路与FoveaBox一直,基于pixel的密集预测。对输出的feature map 每个点(x, y)预测一个4维的向量
\(\boldsymbol{t}{*}=\left(l{}, t^{}, r^{}, b^{}\right)\)[见图一],以及它的标签c∗,在训练过程通过将feature map该点的坐标映射会原图坐标\( \left(\left\lfloor\frac{s}{2}\right\rfloor+ x s,\left\lfloor\frac{s}{2}\right\rfloor+ y s\right) \),其中s为下采样的倍数。若该点落在Groundtruth的框内,且预测的类别c*与GroundTruth的标签c一直,则认为该点(x,y)是正样本,否则认为该点是负样本。如果同一个点(x,y)同时落入了多个Groundtruth区域,则该点应该选择最小的Groundtruth作为回归对象(即图一右图的情况,橙色的点应该回归到蓝色的框)。
Loss Function
L ( { p x , y } , { t x , y } ) = 1 N pos ∑ x , y L cls ( p x , y , c x , y ∗ ) + λ N pos ∑ x , y 1 { c x , y ∗ > 0 } L reg ( t x , y , t x , y ∗ ) \begin{aligned} L\left(\left\{\boldsymbol{p}_{x, y}\right\},\left\{\boldsymbol{t}_{x, y}\right\}\right) &=\frac{1}{N_{\text {pos }}} \sum_{x, y} L_{\text {cls }}\left(\boldsymbol{p}_{x, y}, c_{x, y}^{*}\right) \\ &+\frac{\lambda}{N_{\text {pos }}} \sum_{x, y} \mathbb{1}_{\left\{c_{x, y}^{*}>0\right\}} L_{\text {reg }}\left(\boldsymbol{t}_{x, y}, \boldsymbol{t}_{x, y}^{*}\right) \end{aligned} L({px,y},{tx,y})=Npos 1x,y∑Lcls (px,y,cx,y∗)+Npos λx,y∑1{cx,y∗>0}Lreg (tx,y,tx,y∗)
作者使用了上述公式作为损失函数,\(L_{cls}\)为Focal loss分类损失,\(L_{reg}\)则是IoU loss,且与其他检测的损失函数一样,只有当该点被判断为正样本才计算回归损失。
Inference
测试阶段就比较简单,对feature map上的每个piexl预测它的\(p_{xy}\)和\(t_{xy}\),然后选择\(p_{xy} > 0.05\)的点,将\(t_{xy}\)通过下面的公式扩展成候选框
l ∗ = x − x 0 ( i ) , t ∗ = y − y 0 ( i ) r ∗ = x 1 ( i ) − x , b ∗ = y 1 ( i ) − y \begin{aligned} l^{*} &=x-x_{0}^{(i)}, \quad t^{*}=y-y_{0}^{(i)} \\ r^{*} &=x_{1}^{(i)}-x, \quad b^{*}=y_{1}^{(i)}-y \end{aligned} l∗r∗=x−x0(i),t∗=y−y0(i)=x1(i)−x,b∗=y1(i)−y
Multi Level
作者同样使用了FPN来做一个multi level的多层级预测,之所以这么考虑是基于以下两点:
- 如果像分类一样仅使用下采样倍数最大的一层做检测(感受野过大),会导致大部分小物体漏检
- 若不使用multi level,对于高度重叠的矩形框不太好处理。
这里作者提出了一个观点,大部分重叠的框,都不在同一个尺寸的。只有较少部分是同样尺寸的候选框相互重叠。针对不同尺寸的重叠候选框,利用multi level可以比较好的解决该情况。即不同尺寸的通过不同层级的feature map来回归获得,而针对相同尺寸的候选框重叠,则选择那个面积更小的作为回归。
那作者是如何判断哪个尺寸的候选框由哪个层级的feature map来预测呢,此处作者并未像FoveaBox和FPN一样,而是直接利用回归的结果来判断,即
\(m_{i-1}<\max \left(l^{}, t^{}, r^{}, b^{}\right)
Center-ness for FCOS
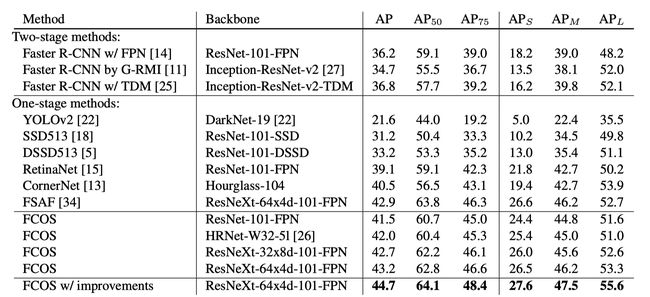
在使用了上述技巧后,作者发现实验得到的结果仍然未达到RetinaNet的实验效果,在分析了实验结果后,作者发现部分误检框离真实框的中心点距离较大,也就是说这部分其实是错得比较离谱的误检,因此作者用一种比较简单的方式减少这种误检,这个方法的核心就是将分类支路的输出乘以一个权重图得到最终的分类置信度。

从图三可以看到,光凭classification得到的score(即前面的\(p_{xy}\))会出现很多的误检框,这些误检框大部分是离中心点距离较大,因此加入了一个分类置信度,输入则是回归支路的得到的结果\(\boldsymbol{t}{*}=\left(l{}, t^{}, r^{}, b^{}\right)\),通过以下公式得到。
c e n t e r n e s s ∗ = min ( l ∗ , r ∗ ) max ( l ∗ , r ∗ ) × min ( t ∗ , b ∗ ) max ( t ∗ , b ∗ ) centerness ^{*}=\sqrt{\frac{\min \left(l^{*}, r^{*}\right)}{\max \left(l^{*}, r^{*}\right)} \times \frac{\min \left(t^{*}, b^{*}\right)}{\max \left(t^{*}, b^{*}\right)}} centerness∗=max(l∗,r∗)min(l∗,r∗)×max(t∗,b∗)min(t∗,b∗)
通过公式,可以比较清楚的了解到,当偏离中心点较大时,centerness的值则较小,因此最后分类得到的置信度也会变小。从而减少了误检框的个数。
Experiment
Summary
在近期阅读了一些Anchor free的方法后,做一些总结;
Anchor free的方法大致可以分为:
1)基于关键点检测沿升到目标检测,其主要解决的问题在于
- 需要寻找哪些关键点?
CornerNet 需要找到左上角点与右下角点,CenterNet(华为)同样需要找到左上角点与右下角点以及中心点,CenterNet(Objects as points)只需要中心点,ExtremeNet则是找到4个极点与中心点 - 关键点如何转换成矩形框?
CornerNet、CenterNet(华为)通过计算左上角点与右下角点Embedding Vector的距离,
CenterNet(Objects as points)通过中心点与回归出来的长宽构成矩形框,ExtremeNet则是通过极点的组合是否包括中心点来判断是否组成矩形框。 - 后处理过程
通过一系列操作,刨除误检框,CenterNet(华为)通过中心点判断其框是否属于误检框等。
2)基于feature map的每个pixel进行dense prediction,其主要解决的问题在于
- 如何定义正负样本点?
FoveaBox 通过设置参数,选取Groundtruth中心点某个范围(参数1)内的点作为正样本点,某个范围外(参数2)的点全部是负样本点,FCOS则是落入Grondtruth中的点均为正样本点,其余的点都为负样本。(FCOS认为这样增加了正样本的数量,而FoveaBox则认为应该选择更精细的点作为正样本) - 如何解决同一个点回归不同的矩形框?
都是采用多层级预测(FPN)来实现,只是两者判断不同尺寸的物体应该由哪一层的特征图来预测的方式不同。
Note
- 作者在将预测点的回归值,转换成候选框的时候(x,y)似乎还是feature map上的坐标,而非原图的坐标,是作者的笔误,还是作者原本就想回归这些偏移量?
- 在Multi Lelve判断时候,直接使用预测的点来判断,是不是没有和GroundTruth联系起来啊?
- centerness是如何训练的?label是否是将原图缩小stride倍,然后根据公式计算得到centerness的真值?