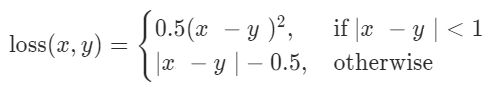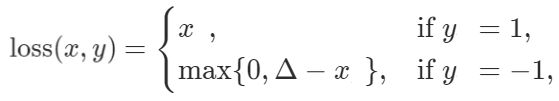Pytorch损失函数篇

点击关注我哦

一篇文章带你了解pytorch中常用的损失函数

Q：什么是损失函数？

训练神经网络类似于人类的学习方式。我们将数据提供给模型，它可以预测某些内容，并告诉其预测是否正确。然后，模型纠正其错误。该模型会重复执行此操作，直到达到我们确定的特定精度水平为止。告诉模型预测错误是正确学习的关键。这是损失函数出现的地方。它告诉模型其估计与实际值相差多远。与人交流虽然比较容易，但要告诉机器，我们需要一种媒介。本篇文章主要介绍常用的几种“媒介”的原理、含义及使用场景。

1.L1范数损失

torch.nn.L1Loss，用来测量平均绝对误差。

其中x是实际值，y是预测值。

含义：

它测量估计值和实际值之间的绝对值，也是错误度量的最简单形式。该误差的值越低，模型越好。我们不能期望它的值为零，因为它可能实际上没有用。总体比较适合处理简单的问题。

使用场景：

+回归问题

+简化模型

+由于神经网络通常用于处理复杂问题，因此很少使用此功能。

2. 均方误差损失 MSELoss

torch.nn.MSELoss，用来测量均方误差（平方L2范数）。

其中x是实际值，y是预测值。

含义：

预测值与实际值之差的平方，换个方式理解：模型会放大较大的损失，并且激励较小的损失。例如：如果分类器的实际差值为200，则错误为40000；如果分类器实际差值为0.1，则错误为0.01。

使用场景：

+回归问题。

+数值特征不大。

+问题不是很高的尺寸。

3. 平滑版L1损失 SmoothL1Loss

torch.nn.SmoothL1Loss，也称为Huber 损失函数，由下式给出：

含义：

如果绝对误差低于1，则使用平方项，否则使用绝对项。它对离群值的敏感性不如均方误差损失，并且在某些情况下可以防止爆炸梯度。在均方误差损失中，我们对差进行平方，得出的差值远大于原始差值。这些高值导致爆炸的梯度。此处避免这种情况，因为对于大于1的数字，数字不平方。

使用场景：

+回归。

+当 要素具有较大的值时。

+非常适合大多数问题。

4. 负对数似然损失 NLLLoss

torch.nn.NLLLoss

负对数似然损失：

含义：

它使数据的整体概率最大化。当它以较小的概率预测正确的类别时，会对模型进行惩罚，而在以较高的概率进行预测时，则对模型进行激励。对数在这里起到惩罚作用。概率越小，对数越高。这里使用负号是因为概率在[0，1]范围内，并且该范围内的值的对数是负数。因此，它使损失值是正的。

使用场景：

+ 分类。

+更快，更小的培训。

+简单的任务。

5. 交叉熵损失 CrossEntropyLoss

torch.nn.CrossEntropyLoss，用来测量预测值和实际值之间的交叉熵。

其中x是真实标签的概率，y是预测标签的概率。

含义：

使用交叉熵作为损失函数可以用来学习数据的概率分布。虽然其他损失函数（如平方损失）会惩罚错误的预测，但是当以高置信度预测错误的预测时，交叉熵会带来更大的损失。与负对数似然损失的区别在于：交叉熵还会惩罚错误但可信的预测以及正确但不太可信的预测，而负对数损失不会根据预测的可信度进行惩罚。

使用场景：

+分类任务

+为了建立自信的模型，即模型不仅可以准确预测，而且还可以更高的概率进行预测。

+获得更高的精度/召回值。

6. Kullback-Leibler散度损失 KLDivLoss

torch.nn.KLDivLoss，其给出了两个概率分布如何彼此不同的度量。

其中x是真实标签的概率，y是预测标签的概率。

含义：

这与交叉熵损失非常相似。区别是预测概率与实际概率之间的差异。这将在模型训练中添加有关信息丢失的数据。预测概率分布离真实概率分布越远，损失越大。它不会像交叉熵损失那样基于预测的置信度对模型进行惩罚，但是预测与地面真实情况有何不同。它通常优于均方误差，尤其是在数据不是正态分布的情况下。交叉熵得到更广泛使用的原因是可以将其分解为交叉熵的函数。最小化交叉熵与最小化KL散度相同。

KL = — xlog（y / x）= xlog（x）— xlog（y）=熵—交叉熵

使用场景：

+ 分类

+交叉熵可以通过较少的计算来实现，因此请避免使用。

7. MarginRankingLoss

torch.nn.MarginRankingLoss，它测量给定输入x1，x2和带有值（1或-1）的标签张量y的损耗。如果y == 1，则假定第一个输入的排名应高于第二个输入，反之亦然。

含义：

分类器的预测y基于输入x1和x2的排名。假设余量的默认值为0，如果y和（x1-x2）具有相同的符号，则损失将为零。这意味着x1 / x2的排名更高（对于y = 1 / -1），正如数据所期望的那样。如果y和（x1-x2）具有相反的符号，则损耗将是y *（x1-x2）给出的非零值。尽管在Pytorch中使用它的方式尚不清楚，但与其他损失函数相比，还没有太多的开源实现和示例。

使用场景：

+ GAN。

+排名任务。

8. HingeEmbeddingLoss

torch.nn.HingeEmbeddingLoss，在输入张量x和包含值（1或-1）的标签张量y的情况下测量损耗。它用于测量两个输入是否相似。

含义：

分类器的预测y基于输入x的值。假设裕度的默认值为1，如果y = -1，那么损失将最大为0和（1 — x）。如果x > 0损耗将是x本身（较高的值），如果0 < x <1损耗将是1 — x（较小的值），并且如果x <0损耗将是0（最小值）。对于y = 1，损耗与x的值一样高。

使用场景：

+学习非线性嵌入

+半监督学习

+要测量两个输入的相似性或相异性。

9. cosine 损失 CosineEmbeddingLoss

torch.nn.CosineEmbeddingLoss，它测量给定输入x1，x2和包含值（1或-1）的标签张量y的损耗。它用于测量两个输入是否相似。

含义：

分类器的预测y基于输入x1和x2的余弦距离。余弦距离是指两点之间的角度。通过使用点乘积可以很容易地找到它：

由于余弦介于-1和+ 1之间，损耗值较小。这有助于计算。假设margin为默认值0，如果y = 1，则损失为（1-cos（x1，x2））。对于y = -1，则损耗将最大为0和cos （x1，x2）。如果cos （x1，x2） > 0，则损耗将是cos （x1，x2）本身（较高的值），如果cos （x1，x2） <0，则损耗将为0（最小值）。

使用场景：

+学习非线性嵌入

+半监督学习

+要测量两个输入的相似性或相异性。

·  END  ·

HAPPY LIFE