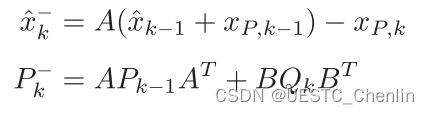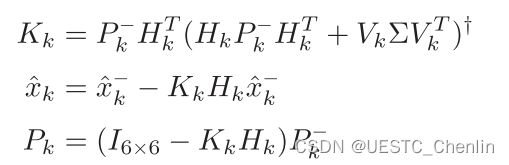通过可见性增强螺旋制导的三维纯方位目标跟踪

原文：Three-Dimensional Bearing-Only Target Following via Observability-Enhanced Helical Guidance

作者：赵世钰

单位：西湖大学

摘要：

本文研究了微型飞行器 (MAV) 的空对空目标跟踪问题，其动机是针对恶意 MAV 的防御应用。当跟踪器 MAV 的机载视觉传感器测量了目标 MAV 的方位时，问题变成了三维 (3-D) 仅方位目标跟踪，这在文献中很少被研究并且面临一些独特的挑战。为了解决这个问题，我们提出了以下新颖的结果。首先，为了从 3-D 方位测量估计目标 MAV 的运动，我们提出了一种新的伪线性卡尔曼滤波器，与扩展卡尔曼滤波器和修正极坐标等经典滤波器相比，它具有简洁的表达和优越的稳定性筛选。其次，我们提出了一种新方法来分析仅方位信息可用时状态估计的可观察性。虽然现有方法适用于 2-D 和单步时间范围情况，但我们的方法可以处理更一般的 3-D 和多步时间范围情况。第三，基于我们的可观察性分析的理论结论，我们设计了一种新的 3-D 螺旋制导律，可以更好地利用 3D 中的额外自由度。制导律适应四轴飞行器的动力学，并设计了基于几何控制的低级飞行控制器。与最先进的算法相比，数值仿真结果验证了所提出算法的优越性能。在实际四旋翼平台上的飞行实验进一步证明了所提算法在实践中的有效性和鲁棒性。

1.引言

近年来，微型飞行器（MAVs）在学术和工业领域得到广泛应用，滥用和恶意使用微型飞行器已经造成了各种问题，例如扰乱机场和威胁公共安全。受这些问题的启发，我们研究了空对空目标跟随任务，其中追击者 MAV 应跟随并与另一个飞行目标 MAV 保持所需距离。对这项任务的研究可能会在未来应用于防御恶意 MAV。

在目标跟踪问题中，大多数现有工作考虑地对地 [1] 和空对地情况 [2]，[3]。少数考虑 3-D 空对空情况 [4 ], [5]，这在技术上更具挑战性，我们稍后会讨论。在 [4] 中，作者研究了协同定位问题，但假设飞行器安装了能够测量目标距离和角度的测距仪，而在我们的工作中，只有方位信息可用。 [4] 中的工作提出了一个控制框架，用于在 3-D 中包围目标。至少需要一个机器人知道目标位置和速度信息，这与我们在两者都不知道的情况下的工作相比是一个主要区别。在作者之前的工作 [6] 中，我们考虑了多智能体编队控制背景下的空对空目标跟随。与 [6] 相比，这项工作考虑了一个更具挑战性的场景，其中目标大小事先未知，因此距离无法直接测量。

实现目标跟随的第一步是通过机载传感器检测目标MAV。由于追踪者微型飞行器的有效载荷限制，视觉是最适合机载传感的解决方案之一。近年来，基于视觉的 MAV 检测受到越来越多的关注，这主要是由于其在 MAV 防御系统中的潜在应用 [7]。在我们最近的工作 [8] 中，我们评估了一些最先进的 MAV 检测深度学习算法，并指出到目前为止，在复杂环境中检测未知 MAV的鲁棒性仍然是一个悬而未决的问题。我们将在未来的工作中专门解决 MAV 的视觉检测，并且仅关注本文中的估计和引导策略。

值得注意的是，当在机载图像中检测到目标MAV时，可以根据相机的固有参数轻松获得相对方位 [9]。但是，由于目标MAV的大小未知，因此无法直接恢复相对距离。这与 [6] 和 [10] 中的场景不同，后者的目标大小是已知的。尽管立体视觉可以估计目标深度，但其实际感应范围通常较短 [11]。

给定目标 MAV 的方位测量，随之而来的任务变成了仅方位的目标跟随问题，这是本文的重点。这样的问题面临一些独特的挑战，如下所述。

1. 第一个挑战是开发稳定的算法，以根据方位测量来估计目标在3-D空间中的运动。尽管到目前为止，许多工作已经研究了目标的仅方位运动分析 (有关详细的文献综述，请参见第II-A节)，但大多数工作仅关注目标和追踪者在二维情况下移动相同的平面。部分原因是，仅方位目标运动分析最初是由军舰在海面上进行跟踪而引起的 [12]。截至目前，3-D空对空案例尚未引起足够的关注。在现有的有关3-D情况的少数研究中，目标方位由两个角度表示: 方位角和仰角。这种表示的缺点是，当高程等于90°时，它具有数学奇异性。更重要的是，双角表示导致卡尔曼滤波器中的高度非线性测量方程，导致目标状态估计的不稳定性或性能退化。
2. 第二个挑战是了解如何利用3-D中的附加自由度 (DoF) 来增强目标的仅方位状态估计的可观察性。可观测性是从方位测量中恢复目标运动的基本要求。除了满足必要和充分的二进制条件，以便系统是可观察的 [13]，追赶者还应充分移动以增强可观察程度，以便可以更准确地估计目标的运动 [14]。尽管已有关于可观察性增强的研究 (有关详细的文献综述，请参见ii-b节)，但3-D案例中的一些基本问题仍然存在。特别地，可观测性增强通常依赖于Fisher信息矩阵 (FIM) [15]。某些指标，如FIM的行列式，可以被视为从方位测量中检索到的目标信息量，通常被最大化以实现最优控制策略 [14]，[16]，[17]，[18]。一个众所周知的基本结论是，后续步骤中追赶者的控制应使目标方位的变化率最大化 (例如，[14]，[16]，[18]，[19]，[20])。这是许多现有最优控制策略的理论基础 [18]，[20]。然而，这样的理论结论仅在一个时间步骤的范围内有效。虽然这不是二维运动的严重问题，但它很好地利用了3-D 情况下的额外 DoF。因此，重要的是在多个时间步长的较长范围内研究最优控制策略。然而，这个问题仍然知之甚少，分析起来也具有挑战性，因为 FIM 的许多指标在 3-D 中不再易于分析处理。通过扩展 FIM 的行列式的表达式可以很容易地验证它，如（7）所示。
3. 第三个挑战是如何为追逐者MAV设计制导和控制策略，以达到预期的控制目标，同时提高可观测性。由于耦合动力学，同时完成这两项任务并非易事。在我们的工作中，控制目标是在追踪者和目标之间保持所需的恒定距离。与这个问题密切相关的是方位目标拦截 [18]、[21]、[22]。然而，现有的目标拦截可观察性增强制导策略无法应用于我们的工作。这是因为目标拦截旨在仅最小化最终未命中距离，而最终拦截速度不受限制。此外，现有的制导律是为非完整模型而不是四旋翼 MAV 模型设计的 [18]、[21]、[22]。在这些非完整模型中，假设速度大小不变，控制目标是设计横向加速度来调整速度方向。另一方面，基于四旋翼 MAV 的可观测性增强目标跟踪尚未在文献中得到解决（参见第 II-C 节的文献综述）。

本文旨在克服上述未解决的挑战。具体来说，本文的贡献和创新点总结如下。

1. 为了估计目标在3-D空间中的运动，我们将3-D目标方位表示为具有测量噪声的单位矢量。通过引入正交投影算子，我们将方位测量从目标位置的非线性函数转换为伪线性函数，因此，线性卡尔曼滤波是适用的。这样，正如我们的仿真结果所验证的那样，方位表示不会遭受任何奇异性，同时，与两角非线性版本相比，估计稳定性更好。
2. 对于 3-D 空间中的可观察性分析，我们引入了一种基于 FIM 的新优化指标。该指标等同于基于 FIM 行列式的流行指标，并且在分析上更易于处理，这意味着我们可以获得其显式表达式，然后计算其梯度以进行优化。通过使用基于行为的方法，我们在受运动约束约束的多个未来步骤的时间范围内对新指标进行了数值优化。据揭露，追击者的最佳策略是在多步视界内沿着嵌入在以目标为中心的 3-D 球体上的椭圆移动。这一新发现概括了先前针对单步视界情况的结果，加深了我们对 3-D 可观测性增强的理论理解，并为我们新的可观测性增强制导律奠定了理论基础。
3. 对于追踪者四旋翼的制导和控制，我们首先设计了一种由横向和纵向命令组成的新的3-D制导律。这里，纵向命令是为了控制到目标 MAV 的相对距离。横向是一种新颖的 3-D 螺旋制导律，旨在提高可观察性。该制导律是根据我们的 3-D 可观测性分析设计的。它驱动 MAV 沿 3-D 螺旋轨迹飞行，从而更好地利用 3-D 空间中的附加自由度，如图 1 所示。为了跟踪高层制导命令，我们最终设计了一个低层飞行基于几何控制方法的控制律，并结合了 MAV 的航向应始终与目标无人机对齐的约束。

给出了广泛的数值模拟结果，以验证该方法的有效性。与最新方法的详细比较证明了所提出方法的卓越性能。此外，已经在实际的四旋翼平台上进行了实验，以验证所提出方法在实践中的有效性和鲁棒性。

2.相关工作：

1. 仅方位目标状态估计Review

卡尔曼滤波作为一种通用的估计框架，广泛应用于纯方位目标估计。在仅方位估计中应用卡尔曼滤波器的一个挑战是测量和要估计的状态之间的非线性。如果使用传统的基于笛卡尔坐标的扩展卡尔曼滤波器 (EKF)，这种非线性将导致估计容易产生偏差甚至发散。已经提出了几种改进的方法来缓解该问题。

第一类有效方法使用修改后的极坐标或球坐标。改进的极坐标 EKF 首次在 [12] 中提出，其中状态变量被仔细选择为方位、方位率、范围的倒数和范围率除以范围。它将三个可观察量与不可观察量（范围的倒数）分开，从而防止误差协方差矩阵病态并确保稳定性。 [23] 中的工作将极坐标方法扩展到球面坐标方法，以通过以其速率增加高程状态来适应 3-D 场景。后来，[24] 中的工作考虑了加速度估计。

第二类是伪线性卡尔曼滤波器 (pseudolinear Kalman filter，PLKF)，最早于 [25] 提出。它通过将非线性测量方程转换为伪线性方程来解决不稳定性问题; 因此，它在计算上是有效的，并且适用于实时系统。但是，这种重铸使噪声变得非高斯，并且与测量矩阵高度相关，从而导致估计偏差。尽管如此，速度估计没有偏差，并且当范围相对较小时，位置偏差小于1% [26]。后来通过引入修正增益方法来缓解偏差问题，其中卡尔曼增益仅作为先验估计的函数计算 [27]。

最近，已经提出了其他基于高级但更复杂的过滤器的方法，例如粒子过滤器 [28]。这些方法计算量大，不适合实时实施，而实时实施对于飞行器的高速运动至关重要。最近的工作是 [29]，其中提出了偏差补偿PLKF。然而，与 [23] 类似，所提出的滤波器中涉及大量非线性三角函数，使得整体表达式相当复杂，从而计算协方差矩阵。

综上所述，现有文献大多考虑二维场景下的方位估计，当涉及到3D时，方位通常用两个角度表示，这会导致潜在的奇异性并使滤波器设计复杂化。

1. 可观测性分析Review

可观测性是纯方位目标运动分析中的一个基本问题。早期的工作主要解决二进制可观察性，即确定系统是否可观察。例如，[25]中的工作构建了一个由状态转移和观察矩阵的时间序列组成的矩阵，并使用其秩来确定二进制可观察性。但是，观察者运动被限制为直线运动。 [13] 中的工作建立了严格的可观察性要求。它表明，当且仅当加速的本船满足指定约束时，可以获得唯一的跟踪解决方案，其中约束是平面上加速度和观察角度的函数。它后来在 [30] 中扩展到 3-D 场景。 [31] 中的工作进一步将 [13] 中的可观察性标准推广到 N 阶目标动力学。

除了确定它是否可观察之外，其他研究人员还专注于量化可观察性。 [16] 中的工作首次将 FIM 引 入可观察性分析。从那时起，FIM 的行列式就成为一种流行的衡量标准。例如，最近在 [17] 和 [18] 中的工作分别使用 Cramer-Rao 下界的特征值和 FIM 的行列式的对数来构建性能指标以最大化可观察性。几何方法利用目标和追赶者在两个连续时刻的几何关系，也被用于推导可观察性的度量，例如[19]和[20]，结果与使用推导的结果一致调频模块。

总之，量化可观察性的一种流行方法是使用 FIM。然而，大多数现有作品只考虑二维场景。尽管 [32] 中的工作考虑了 3-D 情况，但它仅给出了分析可观察性条件。最相关的工作是 [33]，它量化了 3-D 中的可观察性。然而，假设传感器是自由分布的，而在我们的例子中，必须添加一定的空间约束。

1. 可观测性增强机动策略Review

当方位是归位制导的唯一信息源时，通常采用的制导法则，如纯追踪制导 (PPG) 和比例导航制导 (PNG) [34]，通常无法估计目标的状态，从而增加了缺失率。性能恶化的主要原因是由于 [35] 中指出的缺乏距离测量而缺乏可观察性。为了增强可观察性，追赶者必须采取某些机动策略，我们将其分为四类。

第一类包括基于启发式的方法，例如 [35] 和 [36] 中描述的方法，其中将额外的加速命令添加到经典PNG中。可以通过调整机动项的系数来控制机动频率。这种额外的加速度通常是由初始偏航或俯仰角引起的。

第二类包括虚拟状态方法 [21]、[37]。附加虚拟状态通常被选择为横向相对于追击者向下距离的积分。通过将虚拟状态设为零，将轨迹调制为编织模式。通过改变初始值或虚拟状态的数量，可以调制编织模式 [37]。该方法的优点在于结构简单，易于在实际系统中实现。

第三类是间歇策略，首先在[38]中提出。该方案有意关闭常规制导命令以引入制导误差并增加视线（LOS）率，从而增强可观察性。然后在终端归位阶段重新激活制导命令。 [39]、[40]、[41] 中提出了几个具有自适应性的改进版本，其中在决定是否增加或减少承载率之前首先评估可观察性。优点是可以提供足够的轨迹调制以增强可观察性，而不会浪费过多的控制能量，并且可以实时实现。

第四类是基于最优控制的方法，其中目标函数通常是FIM的行列式 [14]，[16]，[42]，[43]。[44] 中的工作提出了一种线性二次制导律，其中在其最优解中考虑了可观测性Gramian。但是，最佳路径具有一个共轭点，该共轭点需要通过调整加权参数来调整其前进时间大于导弹前进时间。否则，共轭点可能导致算法发散。[43] 中的作者提出了 [44] 的改进版本，其中相对速度和与时间平方成比例的变化的可观察性惩罚被认为可以实现更好的可观察性。然而，它们都需要额外的信息，例如时间，这反过来又对估计精度提出了更苛刻的要求。[18] 中的最新工作考虑了合作目标的参与任务，其中假设目标速度的方向是准确已知的，而在我们的跟踪任务中，我们必须对其进行估计。[45] 中的工作提出了针对未知目标的最佳机动策略。但是，他们的目标只是估计目标的状态，而在我们的情况下，我们需要进一步保持期望的范围。

3.问题陈述和系统概述

考虑目标MAV在3-D空间中以恒定速度飞行。假设一个四旋翼平台的追赶者MAV可以使用机载视觉来检测目标，从而获得其相对方位。令pT，vT ∈ R3为目标MAV的位置和速度，p，v ∈ R3为追逐者MAV的位置和速度，均以惯性坐标系表示。追赶者MAV的目标是从任何初始距离的位置接近目标，然后保持所需的相对距离rd>0。

为了实现这一目标，我们设计了一个包括目标估计、制导和飞行控制的复合系统。总体系统架构如图 2 所示。可以看出，视觉系统的输出是带有噪声的方位测量值λ。第一步是设计一个方位观测器来估计目标的位置和速度（见第四节）。然后，有必要分析目标的可观测性并揭示最佳机动策略以增强可观测性（见第五节）。下一步是为追逐者 MAV 设计制导法则以接近目标，同时增强可观察性（参见第 VI 节），从中可以得出追逐者无人机所需的加速度。最后一步是设计低层飞行控制律，包括追逐者 MAV 的所需推力 Td 和扭矩 τd，以跟踪制导命令 ad（参见第 VII 节）。

4.3D纯方位目标估计

 

本节介绍一种新颖的仅方位 PLKF，用于根据 3-D 中的噪声方位测量来估计目标的位置和速度。

A.状态转换方程      

 

B.测量方程

在 (4) 中注意到 ~λ 是 pT 的非线性函数。为了获得线性测量方程，我们引入了一个受我们之前工作启发的正交投影算子 [46]。对于任何非零向量 g ∈ R3，定义正交投影算子

 

对Pg的解释是,对任何向量z，它在垂直于 g 的平面上的正交投影是 Pgz

 

请注意，在 (6) 中，假定 ν 服从正态分布，并且可以将项 rP~λ 视为随时间变化的噪声转移矩阵。通过检查，我们可以得出结论，此转换取决于真实范围 r 和向量 λ 的方向。估计噪声转换矩阵的一个问题是真实范围 r 在实践中是未知的，因此在滤波器中，我们替换(6) 中的 r 与预测值。这种替换已在[29]中使用，并在我们的模拟和实验结果中得到验证是有效的。

1. 3D仅方位PLKF

下面总结了卡尔曼滤波器框架下提出的 3-D 方位观测器的步骤。预测步骤是：

其中 ^x− k 和 P−k 分别是先验状态估计和误差协方差。修正步骤是：

其中 Hk = [Pλk  03×3] , Kk 是观测器增益，Vk = r−k Pλk 并且 rk− 只是 x^− k 的前三个分量的范数，^xk 和 Pk 是后验状态估计和误差协方差，符号†表示伪逆。使用伪逆矩阵的原因是矩阵 (HkP− k HT k +VkΣVT k ) 是秩亏的，因为Hk中的 P~λk 是秩亏的。当逆不存在时，在卡尔曼滤波器中使用伪逆是一种常见的做法，如 [47]、[48]、[49] 所示。

将zk表示为经典卡尔曼滤波器中的测量值。根据 (6)，值得注意的是在我们的模型中zk实际上是 03×1。随着 zk =03×1，更新后验估计 ^xk 的标准步骤因此减少如下：

实际上，度量信息已隐含地包含在矩阵Hk中，这也是伪线性名称的来源，因为Hk是变化的。此外，在二维和三维情况下，观测矩阵Hk具有相同的数学表达式。特别地，Hk可以写为Hk = p〜 λk 0d × d，其中〜 λ ∈ Rd和d是可以为2或3的空间维度。相比之下，当维数从2提升到3时，常用EKF方法的观察矩阵具有更复杂的表达式。这就是统一PLKF或u-PLKF这个名字的创造方式。

5.3D可观性增强

本节介绍了一种在多步范围内增强3-D中仅方位可观测性的新方法。该方法的优点在于，它可以统一二维和三维情况下的可观测性分析，更重要的是，它将现有的可观测性分析从单步视界扩展到多步视界，以便更好地利用3-D中的附加自由度。