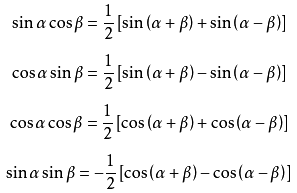离散正(余)弦信号的时域与FFT变换后所得频域之间的关系(幅值和相角)
离散正(余)弦信号的时域与FFT变换后所得频域之间的关系
作者:jbb0523(彬彬有礼)
正弦信号在信号处理中是很常见的,比如通信领域的载波。由于正弦与余弦只是相差π/2的初相,因此这里统称正弦信号。给出连续正弦信号的表达式:
![]()
式中,A为振幅,Ω为模拟角频率(rad/s),φ为初相,f为模拟频率(Hz),Ω=2πf 。
在满足奈奎斯特采样定理条件下对信号x(t)进行采样得到离散正弦信号x(n)
式中,fs为采样频率,Ts为采样间隔,Ts=1/fs,ω为数字角频率(rad),ω=2πf/fs。
根据ω可以判断x(n)的周期性,若2π/ω为有理数则x(n)为周期信号,周期为有理数的分母,详情可参考数字信号处理类教科书。
对N点长的x(n)进行FFT可得其N点长的离散傅里叶变换(DFT),记为X(k)。注意,FFT只是DFT的快速算法的总称。由于x(n)是实信号,所以X(k)为对称的,只须关注其前N/2点即可。
今天要讨论的问题来自一篇文档《为什么要进行傅里叶变换》,这是一篇网上很热门文章,原文出处不详,给出参考链接:网易博客,百度文库,豆瓣。
在原文第七部分“七、用Matlab实现快速傅立叶变换”中有一段话是这样子写的:
假设FFT之后某点n用复数a+bi表示,那么这个复数的模就是An=根号a*a+b*b,相位就是Pn=atan2(b,a)。根据以上的结果,就可以计算出n点(n≠1,且n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn*t+Pn),即2*An/N*cos(2*pi*Fn*t+Pn)。对于n=1点的信号,是直流分量,幅度即为A1/N。
这里用本文的符号翻译一下:对于x(n)的离散傅里叶变换X(k)来说,X(k)一般为复数,可设为X(k)=a(k)+ jb(k),其模值|X(k)|和相角arg[X(k)]分别为对于任意一项X(k)(0
有关模拟频率f与离散频率k的关系可参见数字信号处理类教科书,下面对时域信号幅度相角与离散频域的幅值相角的关系结论进证明。
为了避免频谱泄漏,取f、fs和N均为正整数,且N=mfs,m为正整数。
对离散正弦信号x(n)进行DFT变换:
上面推导过程中使用了欧拉公式和三角函数积化和差公式。令
则![]() 。
。
当mf+k≠0时,根据离散正弦信号的周期性判断方法,我们知道XRe1(k)和XIm1(k)求和式中的正弦信号一定是以N为周期的,所以从0到N-1求和必为零;同理,当mf-k≠0时,XRe2(k)和XIm2(k)求和式中的正弦信号一定是以N为周期的,所以从0到N-1求和也必为零。若要使mf+k项为零,则必有f=k=0,若要使mf-k项为零,则要满足mf=k。
下面以文档《为什么要进行傅里叶变换》中的例子为例来说明:
S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)。式中cos参数为弧度,所以-30度和90度要分别换算成弧度。我们以256Hz的采样率对这个信号进行采样,总共采样256点。
我们取信号S的50Hz成份。这里fs=256Hz,N=256,f=50Hz,m=1,代入得可以通过周期性讨论得知,若k≠50,则必有X(k)=0(当然k=256-50时与k=50对称,前面我们说了只讨论前N/2=128个点)。当k=50时
因此可得时域幅值相角与频域模拟相角的关系
这里模拟频率f与离散频率k的关系为
同理可以讨论f=75Hz成份。对于直流成份,可以认为是如下正弦信号
即f=0Hz,φ=0,代入得
可以通过周期性讨论得知,若k≠0,则必有X(k)=0;当k=0时
其实对于直流成分没有必要这么复杂,直流成分就是一个常数,对常数序列A做DFT
若k≠0,求和项复正弦序列以N为周期,求和后必为零;若k=0,求和通项等于1,则
![]()
推导了半天,可能有些糊涂,最后再把结论清晰的给出来,以便查阅:
【结论1】若有离散正弦信号
对x(n)做N点FFT得X(k),则在0
其中
结论中,为保证k=f/(fs/N)为整数(即不发生频谱泄漏,要求f,fs,N均为正整数,且N=mfs,m为正整数,即N为整数倍的fs)
【结论2】若有直流信号x(n)=A,对x(n)做N点FFT得X(k),则仅在k=0处有值,且此值X=AN,也可以写为A=X/N。
附:三角函数积化和差公式