数据结构——复习五
今天才把字符串匹配搞好,算法真的是不简单,再次复习又多了很多收获
数组和广义表
数组这种数据结构可以看成是线性表的推广。矩阵问题,一般被描述为一个二维数组,当矩阵规模很大且具有特殊结构(对角矩阵,三角矩阵,对称矩阵,稀疏矩阵),为减少程序的时间和空间需求,采用自定义的描述方式。
广义表是另一种推广形式的线性表,是一种灵活的数据结构,在许多方面有广泛的应用。
对于多维数组,将其存放(映射)到内存一维结构时,有个次序约定问题。即必须按某种次序将数组元素排成一列序列,然后将这个线性序列存放到内存中。
二维数组通常有两种顺序存储方式:
设有二维数组A=(aij)mxn,若每个元素占用的存储单元数为l(个),LOC[a11]表示元素a11的首地址,即数组的首地址。
(1)行优先顺序:将数组元素按行排列,第i+1个行向量紧接在第i个行向量后面。对二维数组,按行优先顺序存储的线性序列为:
a11,a12,…,a1n, a21,a22,…a2n ,……, am1,am2,…,amn
由此可知,二维数组中任一元素aij的(首)地址是:
LOC[aij]=LOC[a11]+[(i-1)xn +(j-1)]xl
i=1,2, …,m j=1,2, …,n
(2)列优先顺序:将数组元素按列排列,第j+1个列向量紧接在第j个列向量之后,对二维数组,按列优先顺序存储的线性序列为:
a11,a21,…,am1, a12,a22,…am2, ……, an1,an2,…,anm
由此可知,二维数组中任一元素aij的(首)地址是:
LOC[aij]=LOC[a11]+[(j-1)xm+(i-1)]xl (5-1)
i=1,2, …,n j=1,2, …,m
矩阵的压缩存储
特殊矩阵
1.对称矩阵
存储:对称元素aij和aji(i≠j)分配一个存储空间
需要存储的元素个数:n(n+1)/2

2.三角矩阵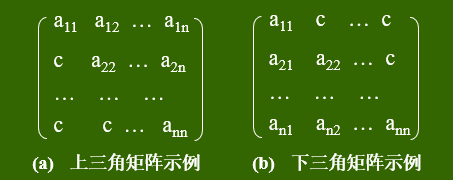
上三角(都用的行优先吧)

下三角

稀疏矩阵
对于稀疏矩阵,目前还没有一个确切的定义。设矩阵A是一个nxm的矩阵中有s个非零元素,设 δ=s/(nxm),称δ为稀疏因子,如果某一矩阵的稀疏因子δ满足δ≦0.05时称为稀疏矩阵。
对于稀疏矩阵,采用压缩存储方法时,只存储非0元素。必须存储非0元素的行下标值、列下标值、元素值。因此,一个三元组(i, j, aij)唯一确定稀疏矩阵的一个非零元素。
1 三元组顺序表
#define MAX_SIZE 101
typedef int elemtype;
typedef struct{
int row;//行下标
int col;//列下标
elemtype value;//元素值
}Triple;
typedef struct{
int mu;//行数
int nu;//列数
int tu;//非0元素个数
Triple data[MAX_SIZE];//下标从1开始使用
}TMatrix;
稀疏矩阵的转置
只写一个快速转置的算法
num[col]:统计A中第col列中非0元素的个数;
cpot[col] :指示A中第一个非0元素在b.data中的恰当位置。
void FastTransMatrix(TMatrix a, TMatrix b)
{
int p,q,col,k;
int num[MAX_SIZE],copt[MAX_SIZE];
b.nu=a.mu;
b.mu=a.nu;
b.tu=a.tu;
//置三元组表b.data的行、列数和非0元素个数
if(b.tu==0)
printf("The Matrix A=0\n");
else
{
for(col=1;col<=a.nu;++col)
num[col]=0;
//向量num[]初始化为0
for(k=1;k<=a.tu;k++)
num[a.data[k].col]++;
//求原矩阵中每一列非0元素个数
cpot[1]=1;
for(col=2;col<=a.nu;col++)
cpot[col]=cpot[col-1]+num[col-1] ;
//求第col列中第一个非0元在b.data中的序号
for(p=1;p<=a.tu;p++)
{
col=a.data[p].col;
q=cpot[col];
b.data[q].row=a.data[p].col;
b.data[q].col=a.data[p].row;
b.data[q].value=a.data[p].value;
cpot[col]++;//至关重要!!当本列中
}
}
}
//前面的rpos[]是代表列
//这个一般应该是按行优先排的序出来的表
两个稀疏矩阵的乘法
设有两个稀疏矩阵A=(aij)mxn,B=(bij)nxp,其存储结构采用行逻辑链接的三元组顺序表。
#define MAX_ROW 100
typedef struct{
int mu,nu,tu;//矩阵的行、列数和非0元个数
Triple data[MAX_SIZE+1];//非0元素的三元组表
int rpos[MAX_ROW];//各行第一个非0位置表
}RLSMatrix;
对于A中的每个元素a.data[p],找到B中所有满足条件:
a.data[p].col=b.data[q].row的元素b.data[q],求得a.data[p].valuexb.data[q].value,该乘积是cij中的一部分。
求得所有这样的乘积并累加求和就能得到cij。
为得到非0的乘积,只要对a.data[1…a.tn] 中每个元素(i,k,aik)(1≦i≦a.rn,1≦k≦a.cn) ,找到b.data中所有相应的元素(k,j,bkj)(1≦k≦b.rn,1≦j≦b.cn) 相乘即可。
则必须知道矩阵B中第k行的所有非0元素,而b.rpos[ ]向量中提供了相应的信息。
b.rpos[row]指示了矩阵B的第row行中第一个非0元素在b.data[ ]中的位置(序号),显然,b.rpos[row+1]-1指示了第row行中最后一个非0元素在b.data[ ]中的位置(序号) 。最后一行中最后一个非0元素在b.data[ ]中的位置显然就是b.tu 。
void MultsMatrix(RLSMatrix a,RLSMatrix b,RLSMatrix &c)
//求矩阵A 、B的积C=AxB,采用行逻辑链接的顺序表
{//当作rpos[]已经存在了
elemtype ctemp[Max_Size+1];
int p,q,arow,ccol,brow,t;
c.mu=a.mu;
c.nu=b.nu;
c.tu=0;//初始化C
for(arow=1;arow<=a.mu;arow++)
{
ctemp[ ]=0;//当前行累加器清零
if(arrow<a.mu)
tp=a.rpos[arow+1];
else
tp=a.tu+1;
for(p=a.rops[arow];p<tp;p++)//都是arow这行的,可能不止一个
{
brow=a.data[p].col;//每一个列
//找到元素在b.data[]中的行号
if(brow<b.mu)
t=b.rpos[brow+1];
else
t=b.tu+1;
for(q=b.rpos[brow];q<t;q++)//b中brow这一行的
{
ccol=b.data[q].col;
//积元素在c中的列号
ctemp[ccol]+=a.data[p].value*b.data[q].value;
}
}//求出c中第arow行中的非0元素
for(ccol=1;ccol<=c.nu;ccol++)//计算arow行ccol列的值
if(ctemp[ccol]!=0)
{
c.tu++;
c.data[c.tu]=(arow,ccol,ctemp[ccol]);
}
}
}
上述时间复杂度相当于O(mxp)。比二维数组的矩阵乘法O(mxnxp)还要好。
十字链表
感觉有点麻烦,还没太看懂,之后再补
广义表
广义表是线性表的推广和扩充,在人工智能领域中应用十分广泛。
广义表(Lists,又称为列表 ):是由n(n ≧0)个元素组成的有穷序列: LS=(a1,a2,…,an),其中ai或者是原子项,或者是一个广义表。
若广义表LS非空时:
◆ a1(表中第一个元素)称为表头;
◆ 其余元素组成的子表称为表尾;(a2,a3,…,an)
◆ 广义表中所包含的元素(包括原子和子表)的个数称为表的长 度。
◆ 广义表中括号的最大层数称为表深 (度)。

注意:
1.A=()这个是特例
2.D=(A,B,C),D是长度为3的广义表,它的3个元素都是子表,因此它的深度是3。
我们重点要知道广义表的长度,深度,表头和表尾
广义表的重要结论:
⑴ 广义表的元素可以是原子,也可以是子表,子表的元素又可以是子表, …。即广义表是一个多层次的结构。
(2) 广义表可以被其它广义表所共享,也可以共享其它广义表。广义表共享其它广义表时通过表名引用。
(3) 广义表本身可以是一个递归表。
(4) 根据对表头、表尾的定义,任何一个非空广义表的表头可以是原子,也可以是子表, 而表尾必定是广义表。
广义表的存储结构
通常用链式存储结构表示,广义表中有两类结点:
◆ 一类是表结点,用来表示广义表项,由标志域,表头指针域,表尾指针域组成;
◆ 另一类是原子结点,用来表示原子项,由标志域,原子的值域组成。
只要广义表非空,都是由表头和表尾组成。即一个确定的表头和表尾就唯一确定一个广义表。
第一种存储方式
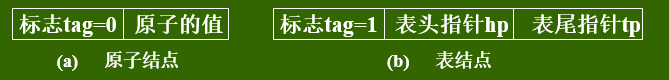

第二种存储方式


//以后慢慢体会这两种方式吧,现在还没有多少感觉,没体会出优缺点来。