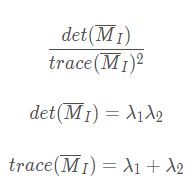计算机视觉——sift特征匹配+opencv(包含sift的低于3.4.3的opencv安装方法)
文章目录
-
- 实验环境
- 环境配置(低于3.4.3的opencv安装方法)
- 虚拟环境的搭建(非必要)
- 局部图像描述子
- Harris 角点检测基本原理
- SIFT特征提取
- 代码实现
- 运行实例
-
- 匹配图像展示
- 匹配结果和分析
实验环境
系统:Ubuntu16.04
语言:python3.7
环境配置(低于3.4.3的opencv安装方法)
本次实验的重头戏之一在于高版本的opencv处于版权保护原因取消了sift函数的使用;在查阅到的资料里,3.4.3以上的版本就无法使用了。
而采用命令行安装时,可以直接是用以下语句进行安装(建立在你已经换过清华源的基础上,大部分人换的应该都是清华源)
pip install opencv-python==3.4.2
但笔者在运行这一步时发现,清华源果然又不能用了,当然这时截止这篇博客撰写时的情况
那么相对的,可以先将上面的语句改成
pip install opencv-python==3.4.2 -i http://pypi.mirrors.ustc.edu.cn/simple/
也就是使用中科大的源,但是截止这篇博客编辑时,此源同样失效
经过多次尝试后,偶然发现阿里的源是可以使用的
pip install opencv-python==3.4.2 -i http://mirrors.aliyun.com/pypi/simple/
如果上述三种常用的国内源都失效的话,可以去git上找找whl手动安装,也是没有问题的。
虚拟环境的搭建(非必要)
linux的命令行操作这里就不详细介绍了,网上同样有大量的教程;这里先建立一个虚拟环境,具体的命令下图所示
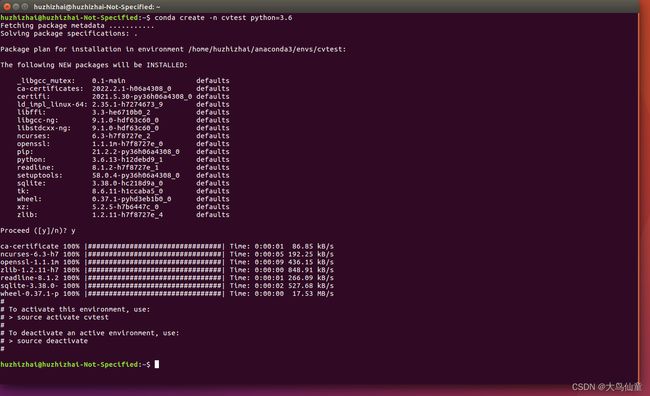
其中建立环境的语句如下
conda create -n cvtest2 python=3.7
这里的cvtest是环境名,可以自行更改,后面的python版本也可以自行更改;值得一提的是,在创建虚拟环境的这一条语句其实后面还可以添加这个环境自己需要包含的包,但习惯上一般不这么做。
那么什么是虚拟环境呢? 简单来说,虚拟环境相当与在电脑中独立的开辟一个容器,在这个容器内所安装的依赖包与外界互不干扰;当我们同时在进行一些依赖包有交叉的不同项目时(如同时处理和进行两个项目,但tensorflow的版本分别为1.1和2.0),为彼此各自建立虚拟环境可以使得彼此都可以独立准确的运行。
事实上,这个实验的环境依赖十分简单,只有一个opencv,不一定需要建虚拟环境,这里这么做只是为了习惯。
局部图像描述子
本次实验的内容是建立在局部图像描述子上的,这个其实是数字图像处理这门课程中有提到的概念。
那么什么是局部图像描述子呢?也就是一种对于图片而言,以一个像素点周围的像素点的分布特征来获取该点的局部特征的算法。
显而易见的,这些特征需要以下性质
- 位移不变性
- 旋转不变性
- 尺度不变性
- 光照不变性
- 以及更多
因此我们学习 Harris 角点检测算法,用于提取图像的特征点;学习 SIFT(尺度不变特征转换),用于解决图像缩放、旋转、曝光、噪声等因素对特征匹配的影响。
Harris 角点检测基本原理
Harris 角点检测算法(也称 Harris & Stephens 角点检测器)是一个极为简单的角点检测算法。该算法的主要思想是:如果像素周围存在多于一个方向的边——即窗口沿任意方向的移动都导致图像灰度的明显变化,我们认为该点为兴趣点。该点就是角点。
简单来说,角点就是那些局部窗口沿各方向移动,均产生明显变化的点或者图像局部曲率突变的点。
换句话说,如果是平坦区域:任意方向移动,无灰度变化;如果是边缘区域:沿边缘方向移动,无灰度变化;如果是角点:艳任意方向移动,明显灰度变化。
其中∇I为包含导数Ix和Iy的图像梯度。由于该定义,MI的秩为1,特征值为λ1=|∇I|和λ2=0。现在对于图像的每个像素,可以计算出该矩阵。
选择权重矩阵W(通常为高斯滤波器Gσ),我们可以得到卷积:

该卷积的目的是得到M在周围像素上的局部平均。计算出的矩阵MI有称为Harris矩阵。W的宽度决定了在像素x周围的感兴趣区域。像这样在区域附近对矩阵M取平均的原因是,特征值会依赖于局部图像特性而变化。如果图像梯度在该区域变化,那么M的第二个特征值将不再为0.如果图像的梯度没有变换,M的特征值也不会变化。
取决于该区域∇I的值,Harris矩阵MI的特征值有三种情况:
- 如果λ1和λ2都是很大的正数,则该x点为角点;
- 如果λ1很大,λ2≈0,则该区域内存在一个边,该区域内的平均MI的特征值不会变化太大;
- 如果λ1≈λ2≈0,则该区域为空。
在不需要实际计算特征值的情况下,为了把重要的情况和其他情况分开,Harris和Stephens在文献中引入了指示函数:
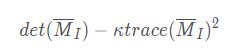
SIFT特征提取
Harris 角点检测算法的结果存在一些不正确的匹配。是因为图像像素块的互相关矩阵具有较弱的描述性。这些描述符还有一个问题,
David Lowe提出的SIFT(Scale-Invariant Feature Transform,尺度不变特征变化)是过去十年中最成功的图像局部描述子之一。SIFT特征包括兴趣点检测器和描述子。SIFT描述子具有非常强的稳定性,这也是SIFT特征能够成功和流行的主要原因。SIFT特征对于尺度、旋转和亮度都具有不变性,因此,它可以用于三维视角和噪声的可靠匹配。
SIFT算法实现步骤简述:
实质上可以归为在不同尺度空间上查找特征点(关键点)的问题。
SIFT算法实现特征匹配主要有三个流程:
- 提取关键点
- 对关键点附加详细信息(局部特征),既描述符;
- 通过特征点(附带上特征向量的关键点)的两两比较找出互相匹配的若干对特征点,建立景物之间的对应关系。
哪些点是SIFT要查找的关键点(特征点)?
SIFT所查找到的关键点(特征点)是一些十分突出,不会因光照,仿射变换和噪音等因素而变化的点,如角点、边缘点、暗区的亮点及亮区的暗点等。
根据归纳,SIFT特征点希望选择出具有下述不变性的点:
- 尺度
- 位移
- 方向
- 光照
代码实现
有了上面的基础概念之后,接下来就可以着手代码的编写。

需要补充的是,由于原图片是手机拍摄,所以像素值过大,代码中存在resize操作,这一步可以去除。
但这里需要注意,事实上压缩图片的尺寸一定程度上会导致原图片的像素分布受影响,这也会使得sift特征匹配的精确度大幅受损。
运行实例

上面展示的就是代码在实际运行中的情况,可以看到4000*3000左右的图片即时经过了0.7的缩放,任然需要花费4s左右的计算时间。
匹配图像展示
事实上本次实验的要求是拍摄校内景物,但由于笔者忘了这茬,所以随手拍的
匹配结果和分析
可以看到匹配的结果是相当不错的,但这是因为两张图的拍摄角度相差不大
事实上,在笔者的多次实验中,当旋转和尺度发生较大的变化时,匹配的效果就已经很差了;一定程度上这也反应出了sift特征提取的一些局限。