机器学习--聚类算法（无监督学习）--K-Menas/BIRCH/CURE/DBSCAN/MDCA算法理论
目录
一 聚类算法概述
1 聚类的概念
2 聚类算法的评价指标
1）轮廓系数（无需目标属性的评价指标）
二 基于划分的聚类算法（K-Means）
1 K-Means算法
1）算法流程
2）算法的优缺点
2 K-Means算法的优化算法
1）K-Medioms（K-中值聚类，用于解决异常数据敏感问题）
2）二分K-Means（弱化初始化簇心的问题，但是依然随机选择簇心）
3）K-Means++算法（弱化初始簇心且不再随机选择簇心，但是簇心之间产生内在有序性）
4）K-Means||（弱化初始簇心且簇心不在具有内在有序性，具有很好的扩展性）
5）Canopy算法（是一种粗粒度的聚类算法，能选择出k个聚簇中心）
3 Mini-Batch K-Means算法
1）算法流程
2）算法效果
三 基于层次的聚类算法
1 算法概念
2 传统的基于层次的聚类算法（不适合大规模数据集，算法效率低，不推荐使用）
1）凝聚的层次聚类算法（AGNES算法，采用自底向上的策略）
2）分裂的层次聚类算法（DIANA算法，采用自顶而下的策略）
3 传统基于层次的聚类算法的优化算法
1）聚类特征树（Cluster-Feature Tree，不推荐使用）
2）平衡迭代削减聚类算法（BIRCH算法，推荐使用）
3）使用代表点的聚类算法（CURE算法，本质上就是AGNES算法，不推荐使用）
四 基于密度的聚类算法
1 算法概念
2 密度相连点的最大集和聚类算法（DBSCAN，推荐使用）
1）相关概念
2）算法流程
3 密度最大值的聚类算法（MDCA，不推荐使用）
1）算法相关概念
2）算法流程
五 基于谱图的聚类算法（不推荐使用）
六 高斯混合聚类（GMM）
一 聚类算法概述
1 聚类的概念
给定数据集（仅有特征属性，无目标属性），依据样本之间的特征属性，将样本聚类为不同聚簇（簇），从而实现簇内样本相异度低，簇间样本相异度高
2 聚类算法的评价指标
1）轮廓系数（无需目标属性的评价指标）
第一步：簇内不相似度（
）
计算当前簇中样本i到簇内所有样本的平均距离，越大代表样本i与当前簇的不相似度越高
第二步：簇间不相似度（
）
计算当前簇中样本i到其他簇所有样本的平均距离，并确定最小平均距离
第三步：
第四步：轮廓系数
（假定样本为m个）
注意：
- 第一点：轮廓系数
![s\subseteq [-1,1]](http://img.e-com-net.com/image/info8/532c9d9b875244a6b97d445f0083b963.gif)
- 第二点：轮廓系数越接近1，表示聚簇越合理，轮廓系数越接近-1，表示聚簇越不合理，轮廓系数越接近0，表示应该在聚簇边界
二 基于划分的聚类算法（K-Means）
1 K-Means算法
1）算法流程
第一步：初始化k个簇心
初始化k个簇心（
），每个聚簇的样本数量，记作
第二步：目标函数（相异度度量采用欧式距离）
第三步：更新簇心（簇内样本的平均值）
第四步：计算样本
到K个簇心的距离，划分到最小距离的簇心聚簇中
第五步：迭代进行更新簇心与重新划分聚簇样本，直到满足中止条件
注意：中止条件
- 第一点：达到最大迭代次数
- 第二点：簇心变化收敛：
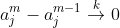
- 第三点：簇心数量
2）算法的优缺点
第一点：优点
- 理解简单，聚类效果不错
- 处理大数据集的时候，该算法保证较好的伸缩性和高效率
- 当簇近似凸状簇（高斯簇）的时候，聚类效果很不错
第二点：缺点
- k值需要事先给定，不同的k值导致不同的聚类效果
- 簇心是初始化随机给定的，不同的初始化簇心会导致不同的聚类效果
- 对异常数据敏感
- 对于非凸型簇，聚类效果不好
2 K-Means算法的优化算法
1）K-Medioms（K-中值聚类，用于解决异常数据敏感问题）
算法流程同K-Means，但是簇心更新采用中值，而非均值
2）二分K-Means（弱化初始化簇心的问题，但是依然随机选择簇心）
第一步：将所有样本作为一个簇，放入队列中
第二步：从队列中选择
（距离误差和）最大的簇，使用K-Means算法划分为两个子簇，并添加队列中
第三步：迭代进行第二步，直到满足中止条件
3）K-Means++算法（弱化初始簇心且不再随机选择簇心，但是簇心之间产生内在有序性）
第一步：从数据集中任选一个样本作为簇心
第二步：计算每个样本到所有簇心的距离和
，基于
注意：基于采用线性概率
选择出前m个最大距离和，进行等概率随机选择，多数都为较大距离和的，而非最大距离，会导致当前簇心选择依赖前面的簇心选择
第三步：迭代进行第二步，直到找到K个聚类中心
4）K-Means||（弱化初始簇心且簇心不在具有内在有序性，具有很好的扩展性）
第一步：从数据中一次抽取k个样本
第二步：重复采样
次（一般5次即可）
第三步：对
个样本，进行K-Means算法，得到K个簇心
第四步：将K个簇心作为初始化簇心，对这个数据集进行K-Means算法
5）Canopy算法（是一种粗粒度的聚类算法，能选择出k个聚簇中心）
第一步：给定样本列表
,以及先验值
第二步：从样本列表
中获取一个节点
，并计算节点
如果没有簇心，把作为新的簇心,，同时删除点，并重复该步骤
第三步：比较簇心距离
与先验值
- 第一点：
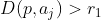
形成一个新的聚簇中心，同时删除点
- 第二点：
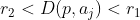
属于该聚簇，添加到该聚簇列表中（不删除点）
- 第三点：
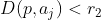
不仅属于该聚簇，而且距离簇心点非常近，平均值法更新簇心，同时删除点
第四步：迭代进行上述步骤，直到达到列表元素不在变化或者列表元素为0的时候
3 Mini-Batch K-Means算法
1）算法流程
第一步：抽取训练集部分数据（训练集小规模子集），使用K-Means算法构建具有k个聚簇中心的模型
第二步：继续抽取训练集部分数据，并添加到距离最近的簇心聚簇中
第四步，采用平均值法更新簇心
第五步：迭代进行第二步、第三步操作，直到满足中止条件（最大迭代次数，簇心变化收敛）
2）算法效果
采用小规模数据子集，使K-Means算法在大数据集上的训练时间减少，同时试图优化目标函数，其效果仅略差于K-Means算法
三 基于层次的聚类算法
1 算法概念
依据样本的特征进行层次的分解，聚类为不同的聚簇，以实现簇内样本相异度低，簇间样本相异度高
2 传统的基于层次的聚类算法（不适合大规模数据集，算法效率低，不推荐使用）
1）凝聚的层次聚类算法（AGNES算法，采用自底向上的策略）
第一步：将每个样本当作一个簇心
第二步：依据某种准则两两合并簇心，得到一个新簇
- 第一点：采用簇间最小距离（SL距离）
两个聚簇中最近距离的两个样本距离
- 第二点：采用簇间最大距离（CL距离）
两个聚簇中最远距离的两个样本距离
- 第三点：采用簇间平均距离（AL距离）
两个聚簇中所有样本的平均距离或者中位值
第三步：反复进行两两合并操作，直到满足中止条件
2）分裂的层次聚类算法（DIANA算法，采用自顶而下的策略）
第一步：将所有样本当作一个聚簇
第二步：依据某种准则细分为更小的聚簇
欧式距离度量
第三步：反复进行细分操作，直到满足中止条件
3 传统基于层次的聚类算法的优化算法
1）聚类特征树（Cluster-Feature Tree，不推荐使用）
第一：重要概念
- 第一点：每个节点都是采用聚类特征表示，聚类特征采用三元组表示
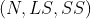
N：每个节点的样本数量
LS：每个节点中样本对应特征维度上的累计加和
SS：每个节点中样本对应特征维度的平方累计加和
- 第二点：父节点的聚类特征CF一定等于其所有子结点的聚类特征CF之和
- 第三点：重要超参：
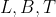
L：内部节点中聚类特征CF最大数量
B：叶子节点中聚类特征CF最大数量（一般认为L=B）
T：聚类特征以簇心中心的最大距离
第二：树的构建
- 第一步：初始状态，CF-Tree为Null，无任何样本
- 第二步：内部节点创建多个CF
读入第一个样本，记作CF1，并用三元组表示
读入第二个样本，判断其到CF1的簇心距离，小于T，划分到该聚簇特征CF1中并更新三元组，大于T，生成一个新的聚类特征CF2，用三元组表示
一直读入样本，直到满足分裂内部节点为止
- 第三步：分裂内部节点
读入新样本，距离所有聚类特征簇心距离都大于T，且聚类特征数量达到最大数量L，需要进行分裂该节点
计算该节点所有聚类特征CF的之间距离，选择最大距离，分裂两个子结点，分别放入这两个最大距离聚类特征
对于剩余聚类特征CF，放入距离最近的聚类特征CF的子结点中
- 第四步：继续读入新数据，迭代进行第一步和第二步操作，直到所有样本读入，停止构建聚类特征树
- 第五步：生成的聚类特征树，每个叶子节点表示一个聚簇
2）平衡迭代削减聚类算法（BIRCH算法，推荐使用）
第一点：将聚类特征树的三个超参，改成两个超参
- 使用分枝因子，取代内部节点或者叶子节点中最大聚类特征数（
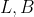） - 使用簇直径，取代簇心最大距离（
）
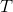注意：从而构建出具有两个参数的聚类特征树
第二点：算法流程同聚类特征数一样
第三点：优势与劣势
- 优势是适合大规模数据集，具有线性效率
- 劣势是不适合非凸型数据
3）使用代表点的聚类算法（CURE算法，本质上就是AGNES算法，不推荐使用）
第一步：将每个样本当作一个簇心
第二步：依据某种准则两两合并簇心，得到一个新簇
距离依然采用AGNES算法中SL/CL/AL距离，但是不计算所有样本，而是从簇中抽取固定数量且分布较好（靠近中心点）的样本点，并将其乘上收缩因子，使其更加靠近中心点，在采用AGNES算法中SL/CL/AL距离计算
第三步：反复进行两两合并操作，直到满足中止条件
注意：执行效率高，不仅可以处理凸型数据，还可以处理非凸型数据
四 基于密度的聚类算法
1 算法概念
依据样本的特征进行密度大小判定，聚类为不同的聚簇，从而实现簇内相异度低，簇间相异度高
注意：其优势在于可以发现非凸型数据，可以克服噪音数据影响，但是
邻域度量依赖距离（高维度特征距离已经不重要），执行效率低
2 密度相连点的最大集和聚类算法（DBSCAN，推荐使用）
1）相关概念
第一点：核心原理
用一个点邻域内样本数量衡量该点所在空间的密度，可以找出任意形状的数据，不受噪音数据影响
第二点：数学符号含义
的邻域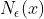
，采用欧式距离
- 密度
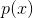
- 阈值
定义核心点使用
- 核心点
点的
，记作点x为核心点；其中所有核心点的集合，记作
- 非核心点（边界点或者噪音点）
点的
，记作点x为非核心点；其中所有非核心点的集合，记作
- 边界点
点为非核心点，但是其邻域存在核心点，记作点为边界点；其中所有的边界点的集合，记作
- 噪音点：
点既不是核心点，也不是边界点，就是噪音点，记作是噪音点；其中所有的噪音点的集合，记作
- 直接密度可达
点是核心点，点
在点的邻域内，称从点到点是直接密度可达的
- 密度可达
存在一个对象链
，满足从
到
是直接密度可达的（一定是核心点），我们称从
到
密度可达
- 密度相连
存在一个对象
，从到是密度可达的，且从到是密度可达的，称
是密度相连的
或者从点到点是直接密度可达（密度可达），称是密度相连的
- 簇C
密度最大：所有满足密度相连的点
密度相连：同一个簇中，所有点都是密度相连的
2）算法流程
第一步：随机抽取样本，出现点
第二步：寻找并合并点
第三步：对剩余样本随机抽取，迭代进行第一步和第二步操作
第四步：抽取完所有样本，算法结束
注意：
不在簇内的样本或者样本过少的簇内样本，可以认为是噪音
仅有两个超参（
邻域，M阈值）需要事先给定
3 密度最大值的聚类算法（MDCA，不推荐使用）
1）算法相关概念
第一点：核心概念
寻找最大密度对象所在的稠密区域
第二点：数学符号含义
- 密度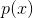（同DBSCAN算法的密度定义）
- 密度阈值
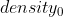（超参）
点的密度大于等于时，认为属于一个比较固定的簇
点的密度小于等于时，暂时认为该点为噪音点
- 最大密度点：
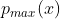
- 有序序列
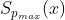（从小到大排列）
- 簇间距离：采用两个簇中最近样本的距离
- 簇间距离阈值：
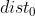（超参）
当两个簇的簇间距离小于给定簇间距离阈值时，两个簇进行合并操作
- 阈值：M（超参）
基本簇中最大样本数量
2）算法流程
第一步：划分基本簇
- 对于数据集
而言：
第一点：计算出最大密度点（大于给定密度阈值），形成以最大密度点为核心的簇
第二点：根据距离公式得到有序序列
，对有序序列中前M个节点，判断节点密度与密度阈值的大小 节点密度大于密度阈值，则将该节点添加到簇中
- 对于剩下数据集
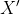（大于给定密度阈值）而言：
第一点：计算出最大密度点，形成以最大密度点为核心的簇
第二点：根据距离公式得到有序序列，对有序序列中前M个节点，判断节点密度与密度阈值的大小
节点密度大于密度阈值，则将该节点添加到簇中
- 迭代处理剩下数据集
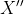，直到数据集中最大密度点小于给定密度阈值，停止迭代
第二步：使用凝聚的层次聚类思想，合并较近的基本簇，得到最终簇
- 第一点：计算所有基本簇的簇间距离，两个簇的簇间距离小于等于给定簇间距离阈值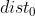，合并两个簇
- 第二点：再次计算此时所有新簇的簇间距离，两个簇的簇间距离小于等于给定簇间距离阈值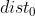，合并两个簇
- 第三点：迭代进行上述操作，直到所有簇的簇间距离均大于给定的簇间距离阈值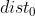，结束迭代
第三步：处理剩下为被划分到基本簇的节点，划分到最近的簇中
常用的方式，计算剩下的样本点距离所有簇的距离，添加到最近距离的簇中
注意：该算法需要给定四个超参（邻域，密度阈值，簇间距离阈值，基本簇最大样本数量）
五 基于谱图的聚类算法（不推荐使用）
有时间便更新
六 高斯混合模型的聚类算法（GMM）
该算法需要使用EM算法思想，接下来博客将单独介绍