EM算法 -- AI基础算法从简单到深

 EM算法就是通常说的让期望最大化的算法，EM算法的核心同时也是基础的部分是最大似然估计，首先通过一个简单的例子来理解EM算法的过程，然后讲解EM在数学上是怎么进行推导和原理证明的，后续会讲解EM算法的应用，也就是高斯混合模型，并且使用GMM做聚类的小案例。

最大似然估计：

例一：
  首先举一个例子，初步理解最大似然估计到底做了什么事情。
  假如去赌场，但是不知道能不能赚钱，你就站在门口，没看到一个人就问是赚了还是赔了，如果问了5个人都说赚了，那么就可以认为赚钱的概率是非常大的，通过观测几个样本，这些样本表现的状态都是赚钱了，自然就会认为赚钱的几率是很大的，总的来说，最大似然估计做的事情就是，当在不知道一个赌场是赚钱还是不赚钱，这个赌场中有一个内在的参数，这个参数控制着他能不能赚钱，通过观察赌场中的每一个样本是不是赚钱，猜测什么参数能够最符合赌场的规则，这个就是极大似然估计要做的事情，就是使用样本进行参数估计的统计学的方法。
 已知样本是分布于某一个模型，然后这个模型当中某些参数是不知道的，比如符合正太分布或者是符合标准的高斯分布，这个时候不知道均值和方差，这个时候想求模型的均值和方差，可以通过观察属于这个分布的一系列的样本，赌场中的这五个人都是属于这个赌场模型的分布，观察这五个人的分布，通过样本的表现状态求解模型的参数，这个就是最大似然估计，最大似然估计当中的最大表示的是通过我的这个样本什么样的模型参数能使得手中的样本，也就是什么参数能正好是的符合观测样本的规则，这个就是极大似然估计，其实就是根据样本反推参数估计，这就是极大似然估计从原理上来说大概做了什么事情。

例二：

  取100个同学的身高数据，这100个人的身高符合某种分布，最可能的是符合一个高斯分布，高斯分布是由两个参数组成的，一个是均值一个是标准差，什么均值和什么方差组成了这个分布呢?什么参数能够使得我恰好抽出的100名学生的概率最大呢?什么样的参数能使得我抽样完的这些数据的概率越大呢?这个就是最大似然估计要做的事情，抽样是随机的抽样，希望参数是符合抽样的规则，参数要跟抽样样本集对的上，他两的对应关系是越大越好的，这个就是最大似然估计要解决的问题，均值和标准差就是模型的参数，高斯分布有均值和方差，假设数据之间是独立同分布的，独立同分布就是说抽第一个人和抽第二个人是没有关系的，X1和X2之间是没有影响的，样本集抽到这100个男生的概率是独立的，相同的，同时抽到这100个样本的概率多大呢?这回就是这100个概率的乘积，也就是第1次抽到X1，是第2次抽到X2，是第3次抽到X3，把他们抽到的概率各自乘在一起，就是同时抽取到这 100个男生的概率，因为是独立的，所以将各自相乘，因为是独立的，所以能让他们相乘，这个就是独立同分布做了一件什么事情。
  观测的不是每一个值，而是抽样抽到的这100个学生身高分布的总体，需要将他进行一个总体的对待，正常情况应该写成什么样子的呢? 正常情况写成累乘积，也就是要进行一个累乘，但是大家观察一个问题，一般情况再求解的时候，经常会求偏导，对于累乘的偏导是很难计算的，为了使得乘法能够求解，一般情况将最大似然估计转换成对数似然估计，转换成对数似然，通过加法进行求解。可以将对数中的乘法转换成加法，加上log之后，求解极大值，求极大值的位置是不会发生变化的，因为只是加上了log函数，没有对内部做什么改变，所以可以在原式的前面加上对数似然，显然可以将累乘变成累加，转换成对数似然函数。求解目标没有发生变化。求解什么参数使得当前样本出现的概率是最大的。
以上就讲清楚了最大似然估计的核心思想，总结就是，已知某个随机样本满足某种概率分布，但是其中分布的具体参数不清楚，通过若干次实验，观察其结果，利用结果计算出参数的大概值。

隐变量：

                                 

  通过上面的讲解，最大似然估计理解起来很简单。现在问题没有这么简单，要将问题进行升级，还是这100个人，这100个不再仅仅是男生身高的分布，这100个人中不仅有男生，还有女生，现在整体样本中多了一个变量，多了一个性别的属性，样本中有男生和女生，现在有两个类别了，男生的身高分布参数时候θ(平均值、方差)，女生的分高分布参数是θ(平均值、方差)，现在有两种参数的分布了，这两个高斯分布是混合在一起的。还是抽取100个人的身高，X1是170，X2是180，但是不知道X1和X2是男生还是女生，可能有一个概率值，X1属于男生的概率是0.7，属于女生的概率是0.3，X2属于男生的概率是0.9，属于女生的概率是0.1，男生和女生都符合高斯分布，但是他们之间的参数是不同的，这就是所谓的均值和方差。
  现在这个问题就有点难了，两个类别，两种分布参数，该怎么进行求解呢?这个就是EM算法中引入的新的问题，这个问题也是很常见的，经常有这样的变量，这个变量有这样的隐含条件，不光包括了身高属性，还包括性别属性等等。这些属性不一定是二分类的，也可能是多分类的，在多分类的参数下，该怎么估计参数呢?这个就是EM算法要求解的目标了。
                                  
  相当于是多了一个隐变量，将隐变量使用一个Z来进行表示，Z=0表示样本来自男生的分布，Z=1表示样本来自女生的分布。左边的式子跟之前的写法是一模一样的，没有发生任何的变化，右边来看，正常只要是x和θ就可以了吧，现在引入了一个隐变量是Z，这个时候对于样本Xi必须要考虑Z等于0和等于1的两种情况，也就是要看男生和女生分别的情况，这里分别有两种情况，所以要将这两种情况分别考虑进来，在这里就是对Z进行求和，有Z=0和Z=1的情况，要将这两种情况都考虑进来就是一个求和，Z=0是0.9，Z=1是0.1，两种可能性相加等于1，也就是将右边的式子进行展开，展开之后引入了隐变量Z，隐变量Z要考虑所有的可能性，所有的可能性中要考虑男生的分布和女生的分布，把他都综合的考虑进来。
求解的目标是什么，求解该怎么进行求解?
  看上边公式，在log中又加上了一个累加和，又加上了这个式子，使得求解就更难了，这种情况直接求偏导就可以了把，但是这个式子直接求解比较困难，按照普遍的方式还是要进行迭代求解的。
  EM算法先不证明，先看一下他是怎么进行整体迭代的。数学上来说还是比较复杂的，但是从实际的迭代流程上看还是比较简单的。

EM算法迭代求解:

                                  

  在赌场当中拿到了两个硬币，在赌场中的硬币跟正常的硬币肯定是不一样的吧，正常的硬币朝上和朝下的几率都是0.5的，但是赌场当中的硬币可能是参假了，正反面朝上的几率是不一样的，我有两枚硬币，刚才的是有两个性别，对于两枚硬币分别相求他的参数的分布，说白了就是朝上的几率和朝下的几率分别是等于多少的，现在的任务都清楚了，现在有两个硬币，这两个硬币朝上和朝下的几率都是不一样的，最终通过一系列的观察，H和T表示朝上和朝下观察的样本的情况，这里就可以通过观察样本的情况，通过样本推断一下两个样本分别朝上和朝下的概率应该是多大是比较合适的，在观察样本之前要进行参数的初始化，先假定一下两枚硬币朝上的概率是多大的。

                                                                                 

 第一步先做假设或者说是初始化参数的值，也就是两个概率值 ，可以按照随机初始化，或者按照经验值进行初始化，按照之前的迭代经验进行初始化， 不要太离谱的，太离谱会需要迭代次数比较多的，初始化的概率最好考虑的比较好，假设A是0.6的几率是正面，假设B是0.5 的几率是正面，对A 和B硬币分别做了参数的假设。
图片
 观察第一个样本，第一个样本不知道是来自A硬币还是来自B硬币，A和B相当于就是隐变量，先得推算来自A的概率有多大，来自B的概率有多大，这是第一步想得到的结果。先知道隐变量的分布是长什么样子的，也就是Z=A的概率和Z=B的概率，这个相当于是E-step，在EM算法中想当于分了两步，一个是E-step，一个是M-step，在E-step中就要估算出隐变量Z等于不同的两种类别A和B的概率分别多大，怎么求呢?
 观察第一个样本，是5正5反的，5个H，5个T，对于5正5反的样本来说。

                                                         
 计算pA和pB的概率值，看一下使用A硬币得到的概率pA和使用B硬币得到的概率pB，pA是一共抛了5次，其中5次是正面朝上，5次负面朝上的，首先计算C(10，5)，这些样本中任意5个样本朝上都是可以的,再乘上0.6(正面朝上)的5次方，再乘上0.4(反面朝上)的5次方，得到pA，同样的可以计算pB，正面朝上的概率是0.5，反面朝上的概率是0.5。
 pA和pB知道了，但是我并不是想知道pA和pB的概率，而是要知道选择A硬币和B硬币的概率，以下面的方式计算选择A硬币和B硬币的概率。 
                                                                 

                
在E-step上根据初始的值和根据样本观察到的结果，得到选择A概率是0.45，选择B的概率是0.55，这个就是E-step做的事情，根据初始的参数的假设，去实际计算一下对应的Z=A和Z=B的概率分别是多大的，现在计算出了选择A的概率0.45，选择B的概率0.55，现在去算一个期望值。
                                                     
对硬币A和硬币B分别进行了统计，都有H和T两种可能，对于A硬币出现H的期望多大呢?正面出现5次，A被选到的概率是0.45，所以选择硬币A，正面朝上的概率是2.2，同理，反面出现5次，A被选到的概率是0.45，所以选择硬币A，反面朝上的概率是2.2，B被选到的概率是0.55，所以选择硬币B，正面朝上的概率是2.8，同理，反面出现5次，B被选到的概率是0.55，所以选择硬币B，反面朝上的概率是2.8，这是当前第一次的估计。
这是计算的第一个样本，现在不光有一个样本，我又N个样本，对于每二个样本，根据样本观测到的结果，都可以根据之前算的流程，来反推pA和pB分别等于多少，得到硬币A的概率的概率和硬币B出现的概率，。
每条样本都计算完之后，计算总和，也就是计算累加和，A硬币正面的期望是21.3，等于A硬币反面的期望是8.6，B硬币正面的期望是11.7，B硬币反面的期望是8.4，然后根据当前的期望反算M-step，根据当前计算的值跟新初始设置的分布，更新A硬币和B硬币初始正面朝上的概率，根据得到的期望结果反过来更新初始化的值。
以下公式计算硬币A正面朝上的概率:        
                                                                    
以下公式计算硬币B正面朝上的概率:
                         
根据期望在反过来更新初始化的参数分布，这样A正面想上的几率和B正面想上的几率就变了，然后使用新的概率进行下一轮的计算，然后下一轮的期望就又会发生变化，让后第二轮E-step昨晚之后还要继续计算M-step。
这个就是EM算法做了一件什么事情。
做到第十步接近于收敛状态了，最终参数不会发生太大的浮动了，这次0.8003，下次0.8002，就是不会有太大的浮动了，认为是接近收敛状态了，最终得到，这是就能说通过EM算法得到了最终的参数的结果等于什么了。这个就是给大家举了一个实际的例子，EM算法从头到尾做了一件什么事情，有一个E-step和M-step，这个就是EM算法该怎么样解决实际的问题。两种概率在有隐变量各自的分布参数应该等于什么的。

Jensen不等式

EM的证明，之前的问题是，样本集中包含了m个独立的样本，有一个类别，隐变量Z，Z是一个未知的，对于这样的问题很难使用最大似然估计进行参数的求解，将要求解的式子写成下面的表达形式，

                                                         

正常求偏导就可以了，现在还有这个求和，要考虑到隐变量，所以只能使用迭代的方法进行求解了，然后证明一下为什么能用这种方法进行求解，证明一下EM算法原理的推导。

                        

 

                        

  正常情况是左边的式子，现在只看一个样本，然后将左边的式子进行展开，展开完之后得到这个样子，将分子和分母分别乘上一个式子Q(z)，乘上Q(z)相当于是乘上Z的分布函数，乘上Z的分布函数目的就是使用Jensen不等式，EM算法能够求解主要就是依赖于这个Jensen不等式，为什么要分子和分母分别乘上一个式子呢?说白了就是要凑一个Jensen不等式。

                        

 

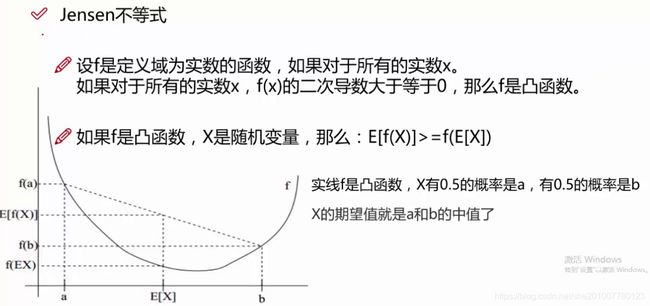
先看一下Jensen不等式做什么事情，先看一下f是定义域为实数的函数，如果对于所有的实数X，f(x)的二次倒数大于等于0，这个时候就说f(x)是凸函数，X平方的二次方等于2，恒大于0，所有是凸函数，。

                                     

左边是函数值的期望，右边是先对X求期望，然后再求期望的函数值，上面的就是Jensen函数，就是凸函数自身有的一个性质，对于这个式子的性质有什么作用呢?一会就会使用这个式子进行一个证明了。

                       

如果是凹函数就是小于等于。反过来。

为什么乘上Q(z)，Q(z)是符合z的分布的概率，对于z的分布的概率，右边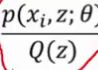是实际的值，那么这个就是的期望。

                         

原式就能写成另外的一种形式，左边是原式的概率，右式是对应的值，将所有的可能性都考虑进来就是一个期望。

Y1的概率是0.5，Y2的概率是0.5,就是求了一个期望。

相当于是先求期望在求log值，log相当于就是f函数，    

                                 

因为log是凹函数，所以有上面这样的不等式，展开得到在展开得到，

                               

刚才说对数中有累加和不好求解，通过Jensen不等式将对数中的累积和提到了外边。提到外边之后就好进行求解了，所以现在使用Jensen不等式得到了一个条件，原式是恒大于右式的，如果右边的式子可以计算最大值，原式永远大于右边的式子，那么原式也能求出一个式子往最大值进行求解的吧。

                                     

可以优化这个下界，使得似然函数最大就可以了，原来是计算左边的式子，现在将求左边的式子转换了一下，转换成了求右边的式子，右边的式子大了，左边的式子显然也要大一点。

                                                       

GMM模型

                                      

    说白了就是说有很多个下界，随着参数的变化使得下界是不断增大的趋势，有了下界之后是一个红色的线，红色的线是横大于等于下界的，优化下界的情况使得上界是恒大于下界的，然后看在什么情况下会使得最符合标准，最能让下界最大了，这个就是求解的目标，不断优化下界进行迭代，进行求解的。

                                     

    什么时候使得似然函数最大呢?显然是去等号的时候，什么时候能使等号成立呢?

                                         

   随机变量是常数的情况下，才能够得到等式成立，只有上边的式子成立了，才能使得等号成立的。

                                         

   等式等于常数有什么规律，这块求和还是会等于1的吧，对于所有的z的可能性始终等于1的，现在将Q(z)的分布函数再进行一个改变，改变之后概率和的结果是1。

                                                        

    这个结果怎么样才能成立呢?要使得上式能够成立，累加和分母不变，加的是分子，分子的和必须等于常数值，等于C的，分母相同的情况下，分子的和必须累加在一起等于C的，等号成立的条件下要求所有的分子是等于C的。

                                

C等于什么。上面说了。

                                                      

上面等于某一个Z的时候的概率值，下面等于所有的可能性，P(Xi)就是所有可能性的结果值.

                                                                   

通过这么长的求解，捣鼓出了E-step该怎么求解。

1、step是根据参数的假设，然后计算pA和pB，然后计算A硬币的概率，通过上面的证明，证明出了step确实是要这么做才能得到这个值。

                                          

再说一下EM算法是干什么的，参考之前的笔记。

数学上看还是比较复杂的，但是实际的迭代更新还是比较简单的。

机器学习怎么做其实不难，但是为什么这么做，推导比较难。很多推导组成了算法的流程的。

                                        

高斯混合模型，可以将我们的数据看做从多个不同的高斯分布中生成出来的，高斯分布就是比较正常的分布，比如数据有男生身高和女生身高，男生身高和女生身高显然是两个不同的高斯分布，所以可以这么假设，GMM是由K个不同的高斯分布生成的，每个高斯分布可以当做是一个组件，那么这个东西的迭代方法类似用于k-means，但是求解是使用EM算法进行求解的，要求解的说白了就是求解每一个分布的参数，只要能求出来某一个分布的参数，那这个问题就求解出来了，先使用E-STEP计算出每个种类的概率，每一次迭代都更新这个概率，再使用已经有的样本被每个种类的概率计算每一次样本的归属，迭代10次之后使用这个样本计算每个分布的参数，平均值或者是均方差。

                                                                         

最终想得到的，比如这里有k1、k2一直到k10，10个高斯分布，一个样本来了如果得到了他的分布，就能算出X1属于K1的概率0.2，属于K2的概率0.7，K3的概率、K4的概率都能计算出他的概率值，对于一个聚类任务。

聚类怎么分类的:

     对于样本来说，能够求出来每一个分布的概率，那他属于哪一个簇不就知道了吗，属于概率最大的簇不就可以了吗?怎么求解说白了和EM算法是一致的，怎么求解，还是每一个分布中的一些系数，一个参数，均值、方差，只要将这些求解出来了，就能知道每个样本来了他属于每一个分布的概率值，这样可以完成非常基本的聚类的任务了。

     推理的时候使用新来的样本，带入每一个分布，使用每一个分布的参数计算得到的概率值，计算得出的概率最大的分布就是这个样本的类别。