Arcface loss实现MNIST数据集（pytorch）

Arcface loss是经过一系列的优化和改进后的结果，因此我们不得不说的是最初始的版本：

Softmax Loss

这是我们传统的Softmax公式，其中， 代表我们的全连接层输出，我们在使损失下降的过程中，则必须提高我们的所占有的比重，从而使得该类的样本更多地落入到该类的决策边界之内.

在Softmax Loss中，由知，特征向量相乘包含由角度信息，即Softmax使得学习到的特征具有角度上的分布特性，为了让特征学习到更可分的角度特性，作者对Softmax Loss进行了一些改进。通过约束||W||=1并且令 bj=0 ,并将  从区分出来，就是为了让特征学习到更可分的角度特性。通过这样的损失函数学习，可以使得学习到的特征具有更明显的角分布，因为决策边界只与角相关。

在此期间作者经过多种改进，包括后来的Center loss、A-softmax loss、consin margin loss等，此处不再赘述。

对于，在满足的情况下，其损失计算公式为 

 

由可以得到，对比CosineFace的，ArcFace中的不仅形式简单，并且还动态依赖于，使得网络能够学习到更多的角度特性。

博主使用MNIST数据集对Arcface loss 的效果进行模拟，代码如下：

arc loss

import torch as t
import torch.nn as nn
import torch.nn.functional as F


class ArcLoss(nn.Module):
    def __init__(self,class_num,feature_num,s=10,m=0.1):
        super().__init__()
        self.class_num=class_num
        self.feature_num=feature_num
        self.s = s
        self.m = t.tensor(m)
        self.w=nn.Parameter(t.rand(feature_num,class_num))       #2*10

    def forward(self,feature):
        feature = F.normalize(feature,dim=1)       #128*2
        w = F.normalize(self.w,dim=0)       #2*10

        cos_theat = t.matmul(feature,w)/10
        sin_theat = t.sqrt(1.0-t.pow(cos_theat,2))
        cos_theat_m = cos_theat*t.cos(self.m)-sin_theat*t.sin(self.m)
        cos_theat_ = t.exp(cos_theat * self.s)
        sum_cos_theat = t.sum(t.exp(cos_theat*self.s),dim=1,keepdim=True)-cos_theat_
        top = t.exp(cos_theat_m*self.s)
        divide = (top/(top+sum_cos_theat))

        # a = torch.acos(cos_theat)
        # top = torch.exp(( torch.cos(a + 0.1)) * 10)  
        # _top = torch.exp(( torch.cos(a)) * 10)
        # bottom = torch.sum(torch.exp(cos_theat * 10), dim=1).view(-1, 1)
        #
        # divide = (top / (bottom - _top + top)) + 1e-10  ##n,10

        return divide
     #以上两种写法逻辑上是一样的，但试验效果不同（反函数求出theat然后直接代入公式的收敛效果略优）

Net

import torch as t
import torchvision as tv
import torch.nn as nn
import torch.nn.functional as F
import torch.utils.data as data
import matplotlib.pyplot as plt
from tensorboardX import SummaryWriter
import torch.optim.lr_scheduler as lr_scheduler
import os

Batch_Size = 128
train_data = tv.datasets.MNIST(
    root="MNIST_data",
    train=True,
    download=False,
    transform=tv.transforms.Compose([tv.transforms.ToTensor(),
                                     tv.transforms.Normalize((0.1307,), (0.3081,))]))

train_loader = data.DataLoader(train_data, batch_size=Batch_Size, shuffle=True, drop_last=True,num_workers=8)

class TrainNet(nn.Module):
    def __init__(self):
        super().__init__()

        self.hidden_layer = nn.Sequential(
            nn.Conv2d(1, 64, 3, 2, 1),
            nn.BatchNorm2d(64),
            nn.PReLU(),
            nn.Conv2d(64,256, 3, 2, 1),
            nn.BatchNorm2d(256),
            nn.PReLU(),
            nn.Conv2d(256,256, 3, 1, 1),
            nn.BatchNorm2d(256),
            nn.PReLU(),
            nn.Conv2d(256,64, 3, 1, 1),
            nn.BatchNorm2d(64),
            nn.PReLU(),
            nn.Conv2d(64,16,3, 2, 1),
            nn.PReLU())
        self.linear_layer = nn.Linear(16*4*4,2)
        self.output_layer = nn.Linear(2,10,bias=False)

    def forward(self, xs):
        feat = self.hidden_layer(xs)
        # print(feature.shape)
        fc = feat.reshape(-1,16*4*4)
        # print(fc.data.size())
        feature = self.linear_layer(fc)
        output = self.output_layer(feature)
        return feature, F.log_softmax(output,dim=1)

def decet(feature,targets,epoch,save_path):
    color = ["red", "black", "yellow", "green", "pink", "gray", "lightgreen", "orange", "blue", "teal"]
    cls = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    plt.ion()
    plt.clf()
    for j in cls:
        mask = [targets == j]
        feature_ = feature[mask].numpy()
        x = feature_[:, 1]
        y = feature_[:, 0]
        label = cls
        plt.plot(x, y, ".", color=color[j])
        plt.legend(label, loc="upper right")     #如果写在plot上面，则标签内容不能显示完整
        plt.title("epoch={}".format(str(epoch+1)))

    plt.savefig('{}/{}.jpg'.format(save_path,epoch+1))
    plt.draw()
    plt.pause(0.01)

Train

from Net import *
from arcloss import ArcLoss

weight = 1
save_path = r"{}\train{}.pt"
save_pic_path = r"D:\PycharmProjects\center_loss\arc_loss_pic\img17"
if __name__ == '__main__':
    net = TrainNet()
    device = t.device("cuda:0" if t.cuda.is_available() else "cpu")
    arcloss = ArcLoss(10, 2).to(device)
    # crossloss = nn.CrossEntropyLoss().to(device)
    nllloss = nn.NLLLoss(reduction="sum").to(device)    #如果reduction="mean"则效果略差
    optmizer = t.optim.SGD(net.parameters(), lr=0.0001, momentum=0.9, weight_decay=0.0005)
    scheduler = lr_scheduler.StepLR(optmizer, 20, gamma=0.8)
    optmizerarc = t.optim.Adam(arcloss.parameters())

    # if os.path.exists(save_path):
    #     net.load_state_dict(t.load(save_path))
    net = net.to(device)
    for epoch in range(15000):
        scheduler.step()
        feat = []
        target = []
        for i, (x, y) in enumerate(train_loader):
            x, y = x.to(device), y.to(device)
            xs, ys = net(x)
            value = t.argmax(ys, dim=1)
            arc_loss = t.log(arcloss(xs))
            nll_loss = nllloss(ys, y)
            arcface_loss = nllloss(arc_loss, y)
            loss =  nll_loss + arcface_loss
            acc = t.sum((value == y).float()) / len(y)
            # loss = crossloss(arc_loss,y)
            optmizer.zero_grad()
            optmizerarc.zero_grad()
            loss.backward()
            optmizer.step()
            optmizerarc.step()

            feat.append(xs)  # 为画图预加载数据,提速
            target.append(y)
            if i % 100 == 0:
                print(epoch, i, loss.item())
                print("acc", acc.item())
                print(value[0].item(), "========>", y[0].item())
        # if (epoch + 1) % 1 == 0:
        #     t.save(net.state_dict(), save_path.format(r"D:\PycharmProjects\center_loss\data", str(epoch)))
        features = t.cat(feat, 0)
        targets = t.cat(target, 0)
        decet(features.data.cpu(), targets.data.cpu(), epoch, save_pic_path)
        #     write.add_histogram("loss",loss.item(),count)
        # write.close()

Effect show

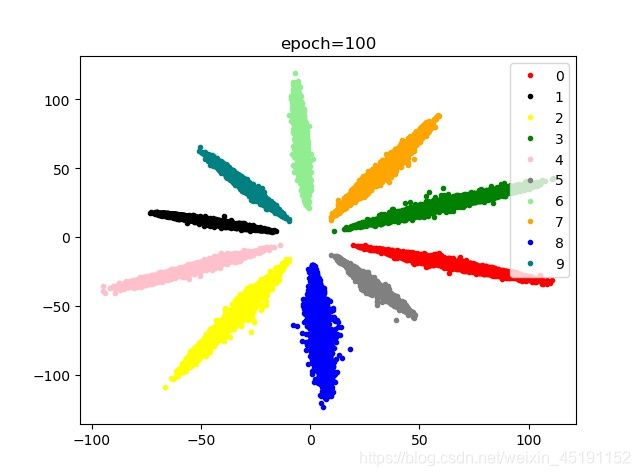BN,SGD+Adam,NLLLOSS(reduction=sum)

 

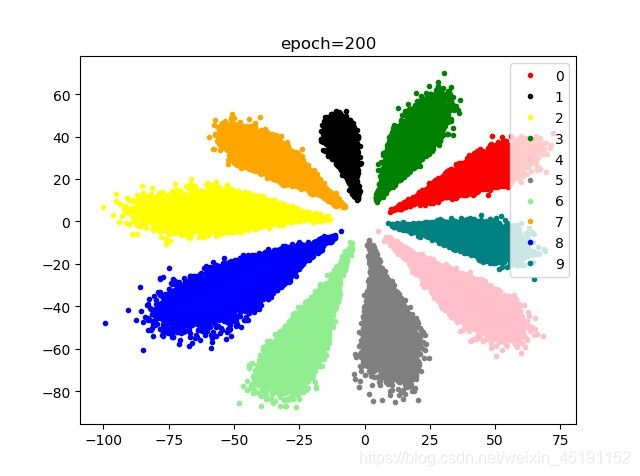BN,SGD+Adam,NLLLOSS(reduction=mean)

 

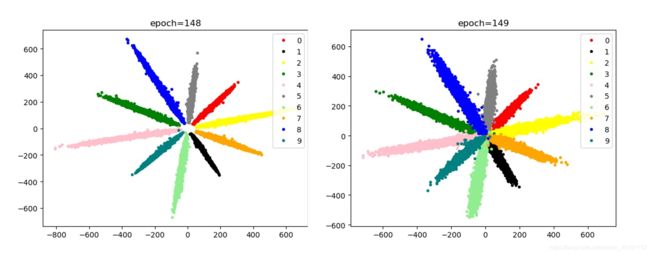Adam+Adam,NLLLOSS(reduction=sum)

 

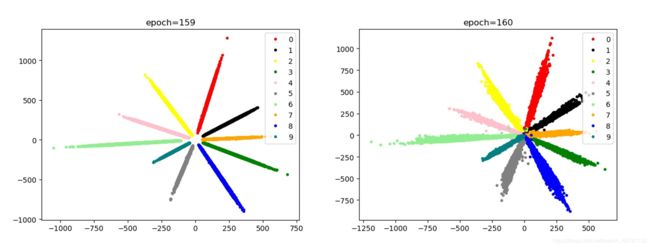BN,Adam+Adam,NLLLOSS(reduction=sum)

 

优化过程总结：

1. 使用SGD优化器很容易出现梯度爆炸问题，但处理好之后效果比较稳定，速度慢是它的鸡肋，希望日后能解决这一问题；
2. 使用Adam分类效果不稳定；
3. 主网络使用BN，NLLLOSS(reduction=sum)对分类效果提升显著；
4. 不知为何，直接求出θ然后将其代入公式的效果比cosθ直接转换公式的分类效果更好一些；
5. 梯度爆炸现象导致原因：

• Arc loss 中s值较大时易出现爆炸，我们使用s=64时第二轮就出现了梯度爆炸，后改为s=10来解决这个问题，s=1的效果略差；
• NLLLOSS中reduction=sum时易出现梯度爆炸，我们采用减小学习率来防止梯度爆炸的出现；
• cos_theat 处给总体“/10”也是为了防止梯度爆炸，做到以上两点可以尝试不适用此方法；
• 使用SGD优化器易出现梯度爆炸（以上两种方法也是针对此优化器做的改进），使用Adam未出现爆炸