【数学建模】-多元线性回归分析
文章目录
-
- 回归的思想
-
- 回归分析:研究X和Y之间相关性的分析。
-
- 相关性
- 因变量Y
- 自变量X
- 回归分析的使命
- 回归分析的分类
- 数据的分类
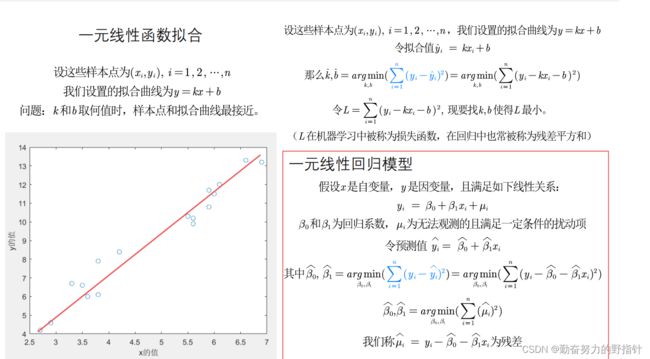
- 一元线性回归
-
- 对于线性的理解
- 回归系数的解释
- 内生性的探究
- 内生性的蒙特卡罗模拟
- 核心解释变量和控制变量
- 回归系数的解释
- 什么时候取对数?
- 四类模型回归系数的解释
- 特殊的自变量:虚拟变量X
-
- 多分类的虚拟变量设置
- 含有交互项的自变量
- 回归实例
-
- 数据的描述性统计
-
- 定量数据
- 定性数据
- Excel中数据透视表
- 11个指标的总体情况介绍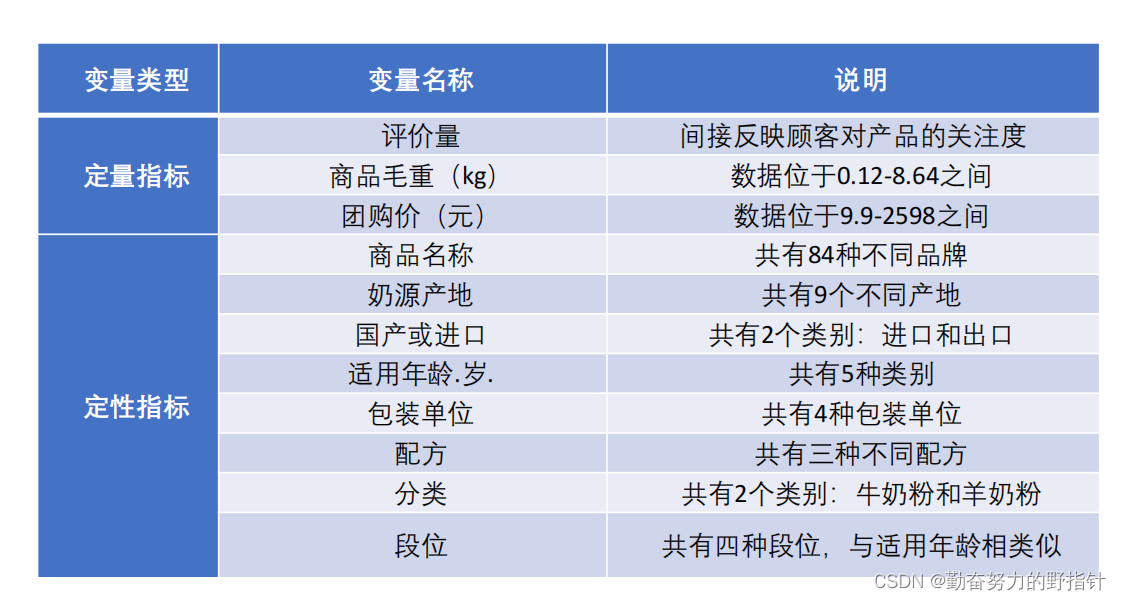
- Stata回归的语句
- 拟合优度 R^2^较低怎么办
- 标准化回归系数
学习来源:清风老师
回归分析的任务就是,通过研究 自变量X和因变量Y的相关关系,尝试去解释Y的形成机制,进而达到通过X去 预测Y的目的。
常见的回归分析有五类: 线性回归、0‐1回归、定序回归、计数回归和生存回归,其划分的依据是因变量Y的类型。
回归的思想
回归分析:研究X和Y之间相关性的分析。
相关性
相关性 ≠ 因果性
在绝大多数情况下,我们没有能力去探究严格的因果关系,所以只好退而求其次,改成通过回归分析,研究相关关系
因变量Y
- 经济学家研究经济增长的决定因素,那么Y可以选取GDP增长率(连续数值型变量)。
- P2P公司要研究借款人是否能按时还款,那么Y可以设计成一个二值变量,Y=0时代表可以还款,Y=1时代表不能还款(0‐1型变量)。
- 消费者调查得到的数据(1表示非常不喜欢,2表示有点不喜欢,3表示一般般,4表示有点喜欢,5表示非常喜欢)(定序变量)。
- 管理学中RFM模型:F代表一定时间内,客户到访的次数,次数其实就是一个非负的整数。(计数变量)
- 研究产品寿命、企业寿命甚至是人的寿命(这种数据往往不能精确的观测,例如现在要研究吸烟对于寿命的影响,如果选取的样本中老王60岁,
现在还活的非常好,我们不可能等到他去世了再做研究,那怎么办呢?直接记他的寿命为60+,那这种数据就是截断的数据)(生存变量)
自变量X
回归分析的任务就是,通过研究X和Y的相关关系,尝试去解释Y的形成机制,进而达到通过X去预测Y的目的。
回归分析的使命
使命1:回归分析要去识别并判断:哪些X变量是同Y真的相关,哪些不是。统计学中有一个非常重要的领域,叫做“变量选择”。(逐步回归法)
使命2:去除了那些同Y不相关的X变量,那么剩下的,就都是重要的、有用的X变量了。接下来回归分析要回答的问题是:这些有用的X变量同Y的相关关系是正的呢,还是负的?
使命3:在确定了重要的X变量的前提下,我们还想赋予不同X不同的权重,也就是不同的回归系数,进而我们可以知道不同变量之间的相对重要性。
第一、识别重要变量;
第二、判断相关性的方向;
第三、要估计权重(回归系数)。
回归分析的分类
数据的分类
横截面数据:在某一时点收集的不同对象的数据。
例如:
(1)我们自己发放问卷得到的数据
(2)全国各省份2018年GDP的数据
(3)大一新生今年体测的得到的数据
时间序列数据:对同一对象在不同时间连续观察所取得的数据
例如:
(1)从出生到现在,你的体重的数据(每年生日称一次)。
(2)中国历年来GDP的数据。
(3)在某地方每隔一小时测得的温度数据。
面板数据:横截面数据与时间序列数据综合起来的一种数据资源。
例如:
2008‐2018年,我国各省份GDP的数据。

数据的收集
一元线性回归
对于线性的理解
回归系数的解释
内生性的探究
包含了所有与y相关,但未添加到回归模型中的变量
如果这些变量和我们已经添加的自变量相关,则存在内生性
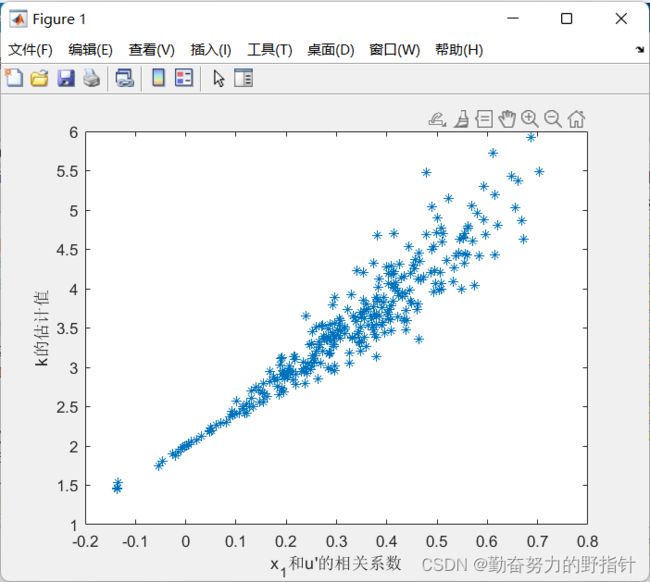
内生性的蒙特卡罗模拟
%% 蒙特卡洛模拟:内生性会造成回归系数的巨大误差
times = 300; % 蒙特卡洛的次数
R = zeros(times,1); % 用来储存扰动项u和x1的相关系数
K = zeros(times,1); % 用来储存遗漏了x2之后,只用y对x1回归得到的回归系数
for i = 1: times
n = 30; % 样本数据量为n
x1 = -10+rand(n,1)*20; % x1在-10和10上均匀分布,大小为30*1
u1 = normrnd(0,5,n,1) - rand(n,1); % 随机生成一组随机数
x2 = 0.3*x1 + u1; % x2与x1的相关性不确定, 因为我们设定了x2要加上u1这个随机数
% 这里的系数0.3我随便给的,没特殊的意义,你也可以改成其他的测试。
u = normrnd(0,1,n,1); % 扰动项u服从标准正态分布
y = 0.5 + 2 * x1 + 5 * x2 + u ; % 构造y
k = (n*sum(x1.*y)-sum(x1)*sum(y))/(n*sum(x1.*x1)-sum(x1)*sum(x1)); % y = k*x1+b 回归估计出来的k
K(i) = k;
u = 5 * x2 + u; % 因为我们回归中忽略了5*x2,所以扰动项要加上5*x2
r = corrcoef(x1,u); % 2*2的相关系数矩阵
R(i) = r(2,1);
end
plot(R,K,'*')
xlabel("x_1和u'的相关系数")
ylabel("k的估计值")
核心解释变量和控制变量
无内生性(no endogeneity)要求所有解释变量均与扰动项不相关。
这个假定通常太强,因为解释变量一般很多(比如,5‐15个解释变量),且需要保证它们全部外生。
是否可能弱化此条件?答案是肯定的,如果你的解释变量可以区分为核心解释变量与控制变量两类。
核心解释变量:我们最感兴趣的变量,因此我们特别希望得到对其系数的
一致估计(当样本容量无限增大时,收敛于待估计参数的真值 )。
控制变量:我们可能对于这些变量本身并无太大兴趣;而之所以把它们也
放入回归方程,主要是为了 “控制住” 那些对被解释变量有影响的遗漏因素。
在实际应用中,我们只要保证核心解释变量与不相关即可。
回归系数的解释
什么时候取对数?
目前,对于什么时候取对数还没有固定的规则,但是有一些经验法则:
(1)与市场价值相关的,例如,价格、销售额、工资等都可以取对数;
(2)以年度量的变量,如受教育年限、工作经历等通常不取对数;
(3)比例变量,如失业率、参与率等,两者均可;
(4)变量取值必须是非负数,如果包含0,则可以对y取对数ln(1+y)
取对数的好处:(1)减弱数据的异方差性(2)如果变量本身不符合正态分布,取
了对数后可能渐近服从正态分布(3)模型形式的需要,让模型具有经济学意义。
四类模型回归系数的解释
特殊的自变量:虚拟变量X
多分类的虚拟变量设置
含有交互项的自变量
回归实例
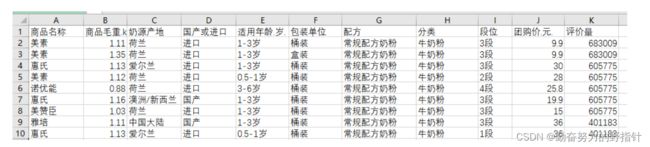
现有某电商平台846条关于婴幼儿奶粉的销售信息,每条信息由11个指标组成。其中,评价量可以从一个侧面反映顾客对产品的关注度。
请对所给数据进行以下方面的分析,要求最终的分析将不仅仅有益于商家,更有益于宝妈们为宝贝选择适合自己的奶粉。
数据的描述性统计
定量数据
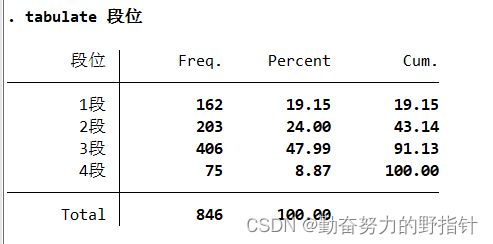
定性数据
// 按键盘上的PageUp可以使用上一次输入的代码(Matleb中是上箭头)
// 清除所有变量
clear
// 清屏 和 matlab的clc类似
cls
// 导入数据(其实是我们直接在界面上粘贴过来的,我们用鼠标点界面导入更方便 本条请删除后再复制到论文中,如果评委老师看到了就知道这不是你写的了)
// import excel "C:\Users\hc_lzp\Desktop\数学建模视频录制\第7讲.多元回归分析\代码和例题数据\课堂中讲解的奶粉数据.xlsx", sheet("Sheet1") firstrow
import excel "课堂中讲解的奶粉数据.xlsx", sheet("Sheet1") firstrow
// 定量变量的描述性统计
summarize 团购价元 评价量 商品毛重kg
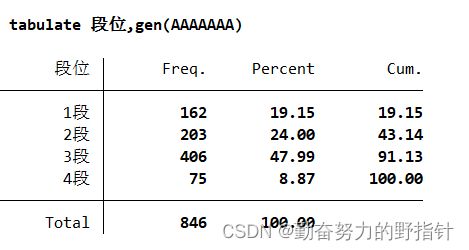
// 定性变量的频数分布,并得到相应字母开头的虚拟变量
tabulate 配方,gen(A)
tabulate 奶源产地 ,gen(B)
tabulate 国产或进口 ,gen(C)
tabulate 适用年龄岁 ,gen(D)
tabulate 包装单位 ,gen(E)
tabulate 分类 ,gen(F)
tabulate 段位 ,gen(G)
// 下面进行回归
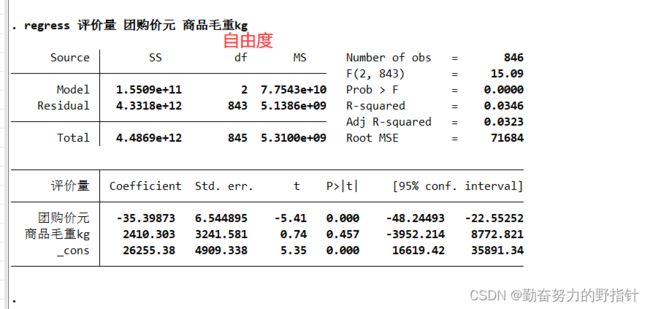
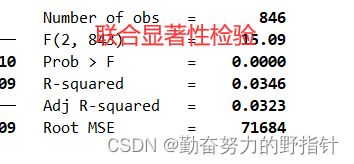
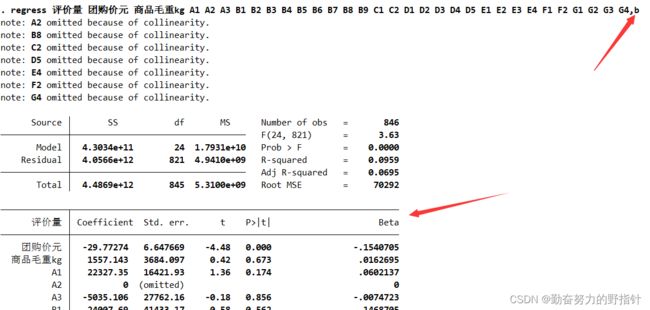
regress 评价量 团购价元 商品毛重kg
// 下面的语句可帮助我们把回归结果保存在Word文档中
// 在使用之前需要运行下面这个代码来安装下这个功能包(运行一次之后就可以注释掉了)
// ssc install reg2docx, all replace
// 如果安装出现connection timed out的错误,可以尝试换成手机热点联网,如果手机热点也不能下载,就不用这个命令吧,可以自己做一个回归结果表,如果觉得麻烦就直接把回归结果截图。
est store m1
reg2docx m1 using m1.docx, replace
// *** p<0.01 ** p<0.05 * p<0.1
// Stata会自动剔除多重共线性的变量
regress 评价量 团购价元 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5 E1 E2 E3 E4 F1 F2 G1 G2 G3 G4
est store m2
reg2docx m2 using m2.docx, replace
// 得到标准化回归系数
regress 评价量 团购价元 商品毛重kg, b
// 画出残差图
regress 评价量 团购价元 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5 E1 E2 E3 E4 F1 F2 G1 G2 G3 G4
rvfplot
// 残差与拟合值的散点图
graph export a1.png ,replace
// 残差与自变量团购价的散点图
rvpplot 团购价元
graph export a2.png ,replace
// 为什么评价量的拟合值会出现负数?
// 描述性统计并给出分位数对应的数值
summarize 评价量,d
// 作评价量的概率密度估计图
kdensity 评价量
graph export a3.png ,replace
// 异方差BP检验
estat hettest ,rhs iid
// 异方差怀特检验
estat imtest,white
// 使用OLS + 稳健的标准误
regress 评价量 团购价元 商品毛重kg A1 A2 A3 B1 B2 B3 B4 B5 B6 B7 B8 B9 C1 C2 D1 D2 D3 D4 D5 E1 E2 E3 E4 F1 F2 G1 G2 G3 G4, r
est store m3
reg2docx m3 using m3.docx, replace
// 计算VIF
estat vif
// 逐步回归(一定要注意完全多重共线性的影响)
// 向前逐步回归(后面的r表示稳健的标准误)
stepwise reg 评价量 团购价元 商品毛重kg A1 A3 B1 B2 B3 B4 B5 B6 B7 B9 C1 D1 D2 D3 D4 E1 E2 E3 F1 G1 G2 G3, r pe(0.05)
// 向后逐步回归(后面的r表示稳健的标准误)
stepwise reg 评价量 团购价元 商品毛重kg A1 A3 B1 B2 B3 B4 B5 B6 B7 B9 C1 D1 D2 D3 D4 E1 E2 E3 F1 G1 G2 G3, r pr(0.05)
// 向后逐步回归的同时使用标准化回归系数(在r后面跟上一个b即可)
stepwise reg 评价量 团购价元 商品毛重kg A1 A3 B1 B2 B3 B4 B5 B6 B7 B9 C1 D1 D2 D3 D4 E1 E2 E3 F1 G1 G2 G3, r b pr(0.05)
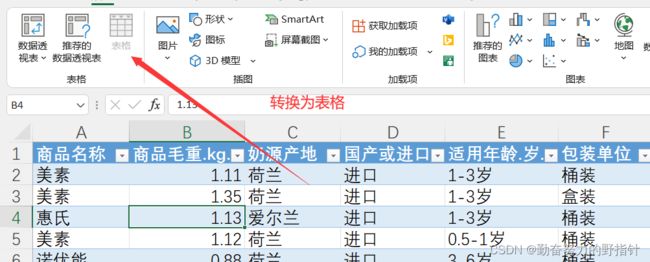
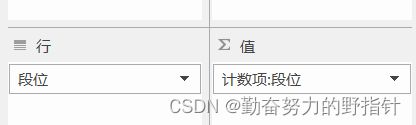
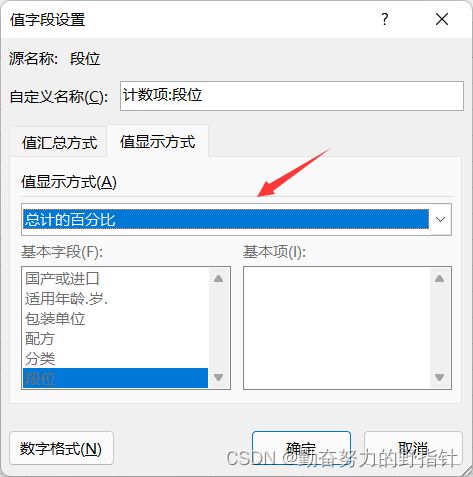
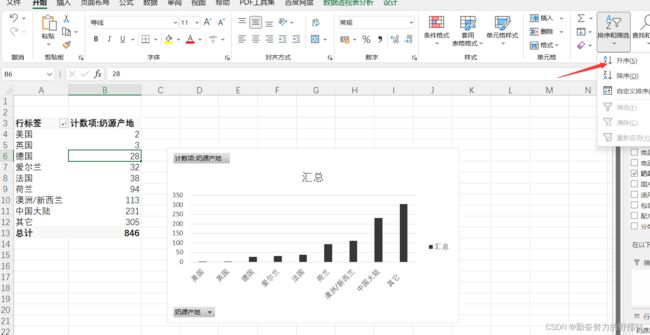
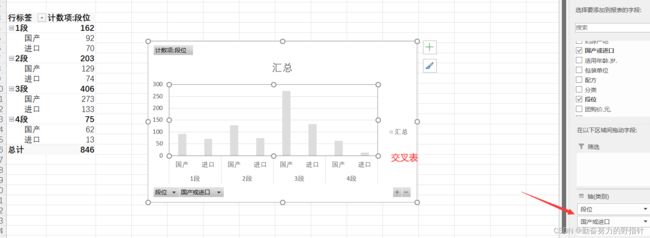
Excel中数据透视表
11个指标的总体情况介绍
Stata回归的语句
拟合优度 R2较低怎么办
(1)回归分为解释型回归和预测型回归。
预测型回归一般才会更看重2 。
解释型回归更多的关注模型整体显著性以及自变量的统计显著性和经济意义显著性即可。
(2)可以对模型进行调整,例如对数据取对数或者平方后再进行回归。
(3)数据中可能有存在异常值或者数据的分布极度不均匀。