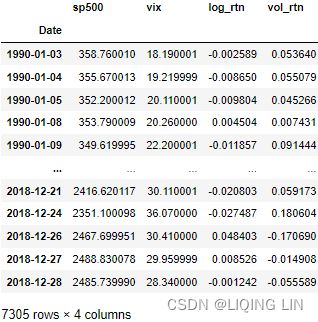
pff1_whylog return Nominal Inflation_CPI_Realized Volati_outlier_distplot_Jarque–Bera_pAcf_sARIMAx

Simple returns VS Log returns

There are two types of returns:

Simple returns(or raw returns): They aggregate over assets; the simple return of a portfolio is the weighted sum of the returns of the individual assets in the portfolio. Simple returns are defined as:
$\small R_t = \frac{P_t - P_{t-1}}{P_{t-1}} = \frac{P_t}{P_{t-1}} - 1$
pct_change() command that gives us the percentage change over the prior period values
Log returns: They aggregate over time; it is easier to understand with the help of an example—the log return for a given month is the sum of the log returns of the days within that month. Log returns are defined as:
$\small r_t = log(\frac{P_t}{P_{t-1}}) = log(P_t) - log(P_{t-1})$ Note: the logarithmic base to use. Default is 'e'

Why use log returns over simple returns? There are several reasons, but the most important of them is normalization, and this avoids the problem of negative prices.

Benefit of using returns, versus prices, is normalization: measuring all variables in a comparable metric, thus enabling evaluation of analytic relationships amongst two or more variables despite originating from price series of unequal values. This is a requirement for many multidimensional statistical analysis and machine learning techniques. For example, interpreting an equity covariance matrix解释股权协方差矩阵 is made sane when the variables are both measured in percentage.

Several benefits of using log returns, both theoretic and algorithmic.
- First, log-normality对数正态性: if we assume that prices are distributed log normally (which, in practice, may or may not be true for any given price series), then $\small log(1+r_i)$ is conveniently normally distributed, because:
  $1+r_t = \frac{P_t}{P_{t-1}} = exp^{ log(\frac{P_t}{P_{t-1}}) }$
  This is handy given much of classic statistics presumes normality.
- Second, approximate raw-log equality近似原始对数相等: when returns are very small (common for trades with short holding durations), the following approximation ensures they are close in value to raw returns(simple return):
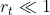
  $log(1+r_t) = log(\frac{P_t}{P_{t-1}}) \approx r_t$ , $r_t\ll 1$
- Third, time-additivity: consider an ordered sequence of n trades. A statistic frequently calculated from this sequence is the compounding return, which is the running return of this sequence of trades over time:
  $(1+r_1) (1+r_2) \cdots (1+r_n) = \prod_{i}^{} (1+r_i)$
  This formula is fairly unpleasant, as probability theory reminds us the product of normally-distributed variables is not normal. Instead, the sum of normally-distributed variables is normal (important technicality: only when all variables are uncorrelated), which is useful when we recall the following logarithmic identity: $log(1+r_t) = log(\frac{P_t}{P_t-1}) = log(P_t) - log(P_{t-1})$
  Thus, compounding returns are normally distributed. Finally, this identity leads us to a pleasant algorithmic benefit; a simple formula for calculating compound returns:
  $\small \sum_{i}^{} log(1+r_i) = log(1+r_1) + log(1+r_2) + \cdots + log(1+r_n) = log(P_n) - log(P_0)$
  Thus, the compound return over n periods is merely the difference in log between initial and final periods. In terms of algorithmic complexity, this simplification reduces O(n) multiplications to O(1) additions. This is a huge win for moderate to large n. Further, this sum is useful for cases in which returns diverge from normal, as the central limit theorem reminds us that the sample average of this sum will converge to normality (presuming finite first and second moments).
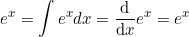
- Fourth, mathematical ease: from calculus, we are reminded (ignoring the constant of integration): $\small e^x = \int e^xdx = \frac{\mathrm{d} }{\mathrm{d} x} e^x = e^x$
  This identity is tremendously useful, as much of financial mathematics is built upon continuous time stochastic processes which rely heavily upon integration and differentiation.
- Fifth, numerical stability: addition of small numbers is numerically safe, while multiplying small numbers is not as it is subject to arithmetic underflow. For many interesting problems, this is a serious potential problem. To solve this, either the algorithm must be modified to be numerically robust or it can be transformed into a numerically safe summation via logs.
- As suggested by John Hall, there are downsides to using log returns. Here are two recent papers to consider (along with their references):
  - Comparing Security Returns is Harder than You Think: Problems with Logarithmic Returns, by Hudson (2010)
  - Quant Nugget 2: Linear vs. Compounded Returns – Common Pitfalls in Portfolio Management, by Meucci (2010)
The difference between simple and log returns for daily/intraday data will be very small, however, the general rule is that log returns are smaller in value than simple returns.
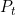$\small P_t$ is the price of an asset in time t. In the preceding case, we do not consider dividends, which obviously impact the returns and require a small modification of the formulas.

The best practice while working with stock prices is to use adjusted values, as they account for possible corporate actions, such as stock splits.

def download(tickers, start=None, end=None, actions=False, threads=True, ignore_tz=True, 
             group_by='column', auto_adjust=False, back_adjust=False, repair=False, keepna=False,
             progress=True, period="max", show_errors=True, interval="1d", prepost=False,
             proxy=None, rounding=False, timeout=10, **kwargs):
    """Download yahoo tickers
    :Parameters:
        tickers : str, list
            List of tickers to download
        period : str
            Valid periods: 1d,5d,1mo,3mo,6mo,1y,2y,5y,10y,ytd,max
            Either Use period parameter or use start and end
        interval : str
            Valid intervals: 1m,2m,5m,15m,30m,60m,90m,1h,1d,5d,1wk,1mo,3mo
            Intraday data cannot extend last 60 days
        start: str
            Download start date string (YYYY-MM-DD) or _datetime.
            Default is 1900-01-01
        end: str
            Download end date string (YYYY-MM-DD) or _datetime.
            Default is now
        group_by : str
            Group by 'ticker' or 'column' (default)
        prepost : bool
            Include Pre and Post market data in results?
            Default is False
        auto_adjust: bool
            Adjust all OHLC automatically? Default is False
        repair: bool
            Detect currency unit 100x mixups and attempt repair
            Default is False
        keepna: bool
            Keep NaN rows returned by Yahoo?
            Default is False
        actions: bool
            Download dividend + stock splits data. Default is False
        threads: bool / int
            How many threads to use for mass downloading. Default is True
        ignore_tz: bool
            When combining from different timezones, ignore that part of datetime.
            Default is True
        proxy: str
            Optional. Proxy server URL scheme. Default is None
        rounding: bool
            Optional. Round values to 2 decimal places?
        show_errors: bool
            Optional. Doesn't print errors if False
        timeout: None or float
            If not None stops waiting for a response after given number of
            seconds. (Can also be a fraction of a second e.g. 0.01)

In this recipe, we show how to calculate both types of returns using Apple's stock prices.

import pandas as pd
import numpy as np
import yfinance as yf

# progress=True : Progress will show a progress bar.
# auto_adjust will overwrite the Close
# Adjust all OHLC automatically? Default is False
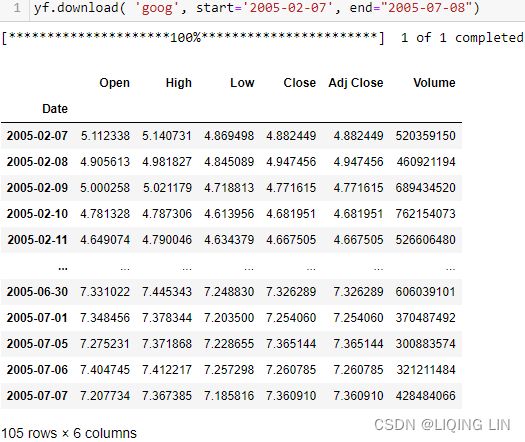
df = yf.download( 'AAPL',
                  start='2000-01-01',
                  end='2010-12-31',
                  progress=False
                )
df

aapl = yf.download( 'AAPL',
                    start='2010-01-01',
                    #end='2010-12-31',
                    progress=False
                  )
aapl

aapl.append(df).sort_index()

aapl.to_csv('aapl')

3. Calculate the simple $\small R_t = \frac{P_t - P_{t-1}}{P_{t-1}} = \frac{P_t}{P_{t-1}} - 1$ and
log returns $\small r_t = log(\frac{P_t}{P_{t-1}}) = log(P_t) - log(P_{t-1})$ using the adjusted close prices:

df['simple_rtn'] = df['Adj Close'].pct_change() # (p_t - p_t_previous)/p_t_previous
df['log_rtn'] = np.log( df['Adj Close']/df['Adj Close'].shift(1) )
df

To calculate the simple returns, we used the pct_change method of pandas Series/DataFrame, which calculates the percentage change between the current and prior element (we can specify the number of lags, but for this specific case, the default value of 1 suffices).
To calculate the log returns, we followed the formula given in the introduction to this recipe. When dividing each element of the series by its lagged value, we used the shift method with a value of 1 to access the prior element. In the end, we took the natural logarithm of the divided values by using np.log .

The first row will always contain a not a number (NaN) value, as there is no previous price to use for calculating the returns.

We will also discuss how to account for inflation in the returns series如何在收益系列中解释通货膨胀. To do so, we continue with the example used in this recipe.

What is an inflation rate?

Inflation rate is the measure of the increase or rate of increase in the general price of selected goods and services over a determined period. Inflation can indicate a decline in the purchasing power or value of a nation's currency and is typically recorded and reported as a percentage.

Inflation rate is important because as the average cost of items increases, currency loses value as it takes more and more funds to acquire the same goods and services as before. This fluctuation in the value of the dollar impacts the cost of living and adversely affects the economy leading to slower economic growth.

The consumer price index

The consumer price index (CPI) is a measure of the overall cost of the goods and services bought by a typical consumer.

The consumer price index is used to monitor changes in the cost of living over time. When the consumer price index rises, the typical family has to spend more money to maintain the same standard of living. Economists use the term inflation to describe a situation in which the economy’s overall price level is rising. The inflation rate is the percentage change in the price level from the previous period. The preceding chapter showed how economists can measure inflation using the GDP deflator. The inflation rate you are likely to hear on the nightly news, however, is calculated from the consumer price index, which better reflects the goods and services bought by consumers.

When the Bureau of Labor Statistics (BLS) calculates the consumer price index and the inflation rate, it uses data on the prices of thousands of goods and services. To see exactly how these statistics are constructed, let’s consider a simple economy in which consumers buy only two goods: hot dogs and hamburgers. Table 1 shows the five steps that the BLS follows.

1. Fix the basket. Determine which prices are most important to the typical consumer. If the typical consumer buys more hot dogs than hamburgers, then the price of hot dogs is more important than the price of hamburgers and, therefore, should be given greater weight in measuring the cost of living. The BLS sets these weights by surveying consumers to find the basket of goods and services bought by the typical consumer. In the example in the table, the typical consumer buys a basket of 4 hot dogs and 2 hamburgers.
2. Find the prices. Find the prices of each of the goods and services in the basket at each point in time. The table shows the prices of hot dogs and hamburgers for three different years.
3. Compute the basket’s cost. Use the data on prices to calculate the cost of the basket of goods and services at different times. The table shows this calculation for each of the three years. Notice that only the prices in this calculation change. By keeping the basket of goods the same (4 hot dogs and 2 hamburgers), we are isolating the effects of price changes from the effects of any quantity changes that might be occurring at the same time.
4. Choose a base year and compute the consumer price index (CPI). Designate one year as the base year, the benchmark against which other years are compared. (The choice of base year is arbitrary, as the index is used to measure changes in the cost of living.) Once the base year is chosen, the index is calculated as follows:

The consumer price index is 175 in 2014. This means that the price of the basket in 2014 is 175 percent of its price in the base year
the consumer price index is 250 in 2015, indicating that the price level in 2015 is 250 percent of the price level in the base year.
5. Compute the inflation rate. Use the consumer price index to calculate the inflation rate, which is the percentage change in consumer price index (CPI) from the preceding period. That is, the inflation rate between two consecutive years is computed as follows:

the inflation rate in our example is 75 percent in 2014 and 43 percent in 2015.

In addition to the consumer price index (CPI) for the overall economy, the BLS calculates several other price indexes. It reports the index for specific metropolitan areas特定大都市地区 within the country (such as Boston, New York, and Los Angeles) and for some narrow categories of goods and services (such as food, clothing, and energy). It also calculates the producer price index (PPI), which measures the cost of a basket of goods and services bought by firms rather than consumers. Because firms eventually pass on their costs to consumers in the form of higher consumer prices, changes in the producer price index are often thought to be useful in predicting changes in the consumer price index.

#############
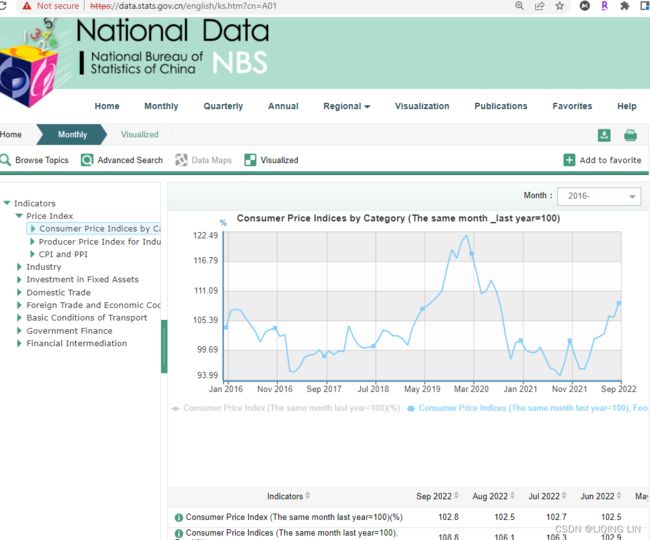
https://data.stats.gov.cn/easyquery.htm?cn=A01

https://data.stats.gov.cn/english/ks.htm?cn=A01

#############USA Consumer Price Index (CPI) | Inflation Rate and Consumer Price Index

What Is the Inflation-Adjusted Return?

The inflation-adjusted return is the measure of return that takes into account the time period's inflation rate. The purpose of the inflation-adjusted return metric is to reveal the return on an investment after removing the effects of inflation.

Removing the effects of inflation from the return of an investment allows the investor to see the true earning potential of the security看到证券的真正盈利潜力 without external economic forces. The inflation-adjusted return is also known as the real rate of return or required rate of return adjusted for inflation(The real rate of return on an investment measures the increase in purchasing power that the investment provides.).

The inflation-adjusted return accounts for the effect of inflation on an investment's performance over time.
Also known as the real return, the inflation-adjusted return provides a more realistic comparison of an investment's performance.
Inflation will lower the size of a positive return and increase the magnitude of a loss.

The inflation-adjusted return is useful for comparing investments, especially between different countries because each country's inflation rate is accounted for in the return. In this scenario, without adjusting for inflation across international borders, an investor may get vastly different results when analyzing an investment's performance. The Inflation-adjusted return serves as a more realistic measure of an investment's return when compared to other investments.

example

assume a bond investment is reported to have earned 2% in the previous year. This appears like a gain. However, suppose that inflation last year was 2.5%. Essentially, this means the investment did not keep up with inflation, and it effectively lost 0.5%.

Assume also a stock that returned 12% last year and inflation was 3%. An approximate estimate of the real rate of return is 9%, or the 12% reported return less the inflation amount (3%).

We first download the monthly Consumer Price Index (CPI) values from Quandl and calculate the percentage change (simple return) in the index. We can then merge the inflation data with Apple's stock returns通胀数据与苹果的股票收益合并, and account for inflation计算通胀 by using the following formula:
$\small R_t ^{r} = \frac{1+R_t}{1+\pi_t} - 1$ OR
Here, $\small R_t$ is a time t simple return and $\small \pi_t$ is the inflation rate.

Calculating the inflation-adjusted return requires three basic steps.

First, the return on the investment must be calculated.
Second, the inflation for the period must be calculated.
And third, the inflation amount must be geometrically backed out of the investment's return.通货膨胀金额必须以几何方式从投资回报中扣除。

Example of Inflation-Adjusted Return

Assume an investor purchases a stock on January 1 of a given year for $75,000. At the end of the year, on December 31, the investor sells the stock for $90,000. During the course of the year, the investor received $2,500 in dividends. At the beginning of the year, the Consumer Price Index (CPI) was at 700. On December 31, the CPI was at a level of 721.

The first step is to calculate the investment's return using the following formula:
Return = (Ending price - Beginning price + Dividends) / (Beginning price)
= ( $90,000 - $75,000 + $2,500 ) / $75,000
= 23.3% percent.
The second step is to calculate the level of inflation over the period using the following formula:
Inflation = (Ending CPI level - Beginning CPI level) / Beginning CPI level
= ( 721 - 700 ) / 700
= 3 percent
The third step is to geometrically back out the inflation amount using the following formula:
Inflation-adjusted return = (1 + Stock Return) / (1 + Inflation) - 1
= ( 1.233 / 1.03 ) - 1
= 19.7 percent

Nominal Return vs. Inflation-Adjusted Return

Using inflation-adjusted returns is often a good idea because they put things into a very real-world perspective. Focusing on how investments are doing over the long-term can often present a better picture when it comes to its past performance (rather than a day-to-day, weekly, or even monthly glance).

But there may be a good reason why nominal returns work over those adjusted for inflation. Nominal returns are generated before any taxes, investment fees, or inflation. Since we live in a “here and now” world, these nominal prices and returns are what we deal with immediately to move forward. So, most people will want to get an idea of how the high and low price of an investment is—relative to its future prospects—rather than its past performance. In short, how the price fared when adjusted for inflation five years ago won’t necessarily matter when an investor buys it tomorrow.

Example

The nominal rate of return on an investment is the return that the investment earns expressed in current dollars. For example, if you put $50 into an investment that promises to pay 3% interest, at the end of the year you will have $51.50 (the initial $50 plus a $1.50 return). Your nominal return is 3%, but this does not necessarily mean that you are better off financially at the end of the year because the nominal return does not take into account the effects of inflation.

To continue the example, assume that at the beginning of the year, one bag of groceries costs $50. During the year, suppose grocery prices rise by 3%. This means that by the end of the year one bag of groceries costs $51.50. In other words, at the beginning of the year you could have used your $50 either to buy one bag of groceries or to make the investment that promised a 3% return. If you invested your money rather than spending it on groceries, by the end of 1 year you would have had $51.50, still just enough to buy one bag of groceries. In other words, your purchasing power did not increase at all during the year. The real rate of return on an investment measures the increase in purchasing power that the investment provides. In our continuing example, the real rate of return is 0%(or ) even though the nominal rate of return is 3%. In dollar terms, by investing $50 you increased your wealth by 3% to $51.50, but in terms of purchasing power you are no better off because your money is only enough to buy the same amount of goods that it could have bought before you made the investment. In mathematical terms, the real rate of return is approximately equal to the nominal rate of return minus the inflation rate.

Example

Suppose you have $50 today and are trying to decide whether to invest that money or spend it.

If you invest it, you believe that you can earn a nominal return of 10%, so after 1 year your money will grow to $55.
If you spend the money today, you plan to feed your caffeine habit by purchasing 20 lattes at your favorite coffee shop at $2.50 each.

You decide to save and invest your money, so a year later you have $55. Unfortunately, during that time inflation caused the price of a latte to increase by 4.8% from $2.50 to $2.62(=2.5*1.048). At the new price, you can just about afford to buy 21 lattes (21 × $2.62 = $55.02). That extra latte represents an increase in your purchasing power of 5% (i.e., 21 is 5% more than 20), so your real return(or) on the investment is 5% because it enabled you to buy 5% more than you could before you invested. Notice that the real return is approximately equal to the difference between the investment’s nominal return (10%) and the inflation rate (4.8%).

Execute the following steps to account for inflation in the returns series.

import pandas as pd
import quandl

QUANDL_API_KEY = 'sKqHwnHr8rNWK-3s5imS'
quandl.ApiConfig.api_key = QUANDL_API_KEY

df_all_dates = pd.DataFrame( index=pd.date_range( start='1999-12-31',
                                                  end='2010-12-31'
                                                )
                           )
df = df_all_dates.join( df[ ['Adj Close'] ], 
                        how ='left'    
                      ).fillna( method='ffill').asfreq('M')
                      #Convert time series to specified frequency
df

df_all_dates.join( df[ ['Adj Close'] ],.join(how='left') foward-fill resample
==>==>==>

We used a left join, which is a type of join (used for merging DataFrames) that returns all rows from the left table and the matched rows from the right table while leaving the unmatched rows empty.
In case the last day of the month was not a trading day, we used the last known price of that month( fillna(method=' ffill' ) ).
Lastly, we selected the end-of-month rows only by applying asfreq(' M' ) .

Download the inflation data from Quandl:

# Download the inflation data from Quandl:
# Consumer Price Index (CPI)
df_cpi = quandl.get( dataset='RATEINF/CPI_USA',
                     start_date = '1999-12-01',
                     end_date = '2010-12-31'
                   )
df_cpi.rename( columns={'Value':'cpi'},
               inplace=True
             )
# Merge the inflation data to the prices: 
df_merged = df.join(df_cpi, how='left')
df_merged

=>=><=

5. Calculate the simple returns $\small R_t = \frac{P_t - P_{t-1}}{P_{t-1}} = \frac{P_t}{P_{t-1}} - 1$ and inflation rate(the inflation rate between two consecutive years):

df_merged['simple_rtn'] = df_merged['Adj Close'].pct_change()
df_merged['inflation_rate'] = df_merged.cpi.pct_change()
df_merged

6. Adjust the returns for inflation:
$\small R_t ^{r} = \frac{1+R_t}{1+\pi_t} - 1$ OR

df_merged['real_rtn'] = ( df_merged.simple_rtn + 1)\
                            /(df_merged.inflation_rate -1 )-1
df_merged

The DataFrame contains all the intermediate results, and the real_rtn column contains the inflation-adjusted returns.

######################

import pandas as pd
import numpy as np
import yfinance as yf

# progress=True : Progress will show a progress bar.
# auto_adjust will overwrite the Close
# Adjust all OHLC automatically? Default is False
df = yf.download( 'AAPL',
                  start='2000-01-01',
                  #end='2010-12-31',
                  progress=False
                )
df

df['simple_rtn'] = df['Adj Close'].pct_change() # (p_t - p_t_previous)/p_t_previous
df['log_rtn'] = np.log( df['Adj Close']/df['Adj Close'].shift(1) )
df

import pandas as pd
import quandl

QUANDL_API_KEY = 'sKqHwnHr8rNWK-3s5imS'
quandl.ApiConfig.api_key = QUANDL_API_KEY

df_all_dates = pd.DataFrame( index=pd.date_range( start=df.index[:1][0],
                                                  end=df.index[-1:][0]
                                                )
                           )
df = df_all_dates.join( df[ ['Adj Close'] ], 
                        how ='left'    
                      ).fillna( method='ffill').asfreq('M')
                      #Convert time series to specified frequency

# Download the inflation data from Quandl:
# Consumer Price Index (CPI)
df_cpi = quandl.get( dataset='RATEINF/CPI_USA',
                     start_date = df.index[:1][0],
                     end_date = df.index[-1:][0]
                   )
df_cpi.rename( columns={'Value':'cpi'},
               inplace=True
             )
# Merge the inflation data to the prices: 
df_merged = df.join(df_cpi, how='left')
df_merged

inflation_rate = quandl.get( dataset='RATEINF/inflation_USA',
                             start_date = '1999-12-01',
                           )
inflation_rate.rename( columns={'Value':'inflation_rate'},
                       inplace=True
                     )
# Merge the inflation data to the prices: 
df_merged = df_merged.join(inflation_rate, how='left')

df_merged['simple_rtn'] = df_merged['Adj Close'].pct_change()
df_merged['inflation_rate_from_cpi'] = df_merged.cpi.pct_change()

df_merged['real_rtn'] = ( df_merged.simple_rtn + 1)\
                            /(df_merged.inflation_rate -1 )-1
df_merged

import matplotlib.pyplot as plt
plt.style.use('seaborn')

fig, ax = plt.subplots( 1,1, figsize=(10,8) )

date='2021-01-01'
#df_merged.loc[df.index>'2019-01-01']['real_rtn'].plot()
ax.plot( df.index[df.index>date],
         df_merged.loc[df.index>date]['inflation_rate'],
         label='inflation_rate',
         color='blue'
       )
ax.plot( df.index[df.index>date],
         df_merged.loc[df.index>date]['inflation_rate_from_cpi'],
         label='inflation_rate_from_cpi',
         color='green'
       )
ax.plot( df.index[df.index>date],
         df_merged.loc[df.index>date]['real_rtn'], 
         label='aapl real_rtn',
         color='r'
       )


plt.setp( ax.get_xticklabels(), rotation=45, horizontalalignment='right', fontsize=14 )
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.legend(loc='best', fontsize=14)
plt.show()

######################

Changing frequency

The general rule of thumb for changing frequency can be broken down into the following:

Multiply/divide the log returns by the number of time periods.
Multiply/divide the volatility by the square root of the number of time periods.

In this recipe, we present an example of how to calculate the monthly realized volatilities for Apple using daily returns and then annualize the values.

What is Realized Volatility?

Realized volatility is the assessment of variation in returns for an investment product by analyzing its historical returns within a defined time period.(that is, the observed volatility of the underlying returns from historical market prices.)

Assessment of degree of uncertainty and/or potential financial loss/gain from investing in a firm may be measured using variability/ volatility in stock prices of the entity.
In statistics, the most common measure to determine variability is by measuring the standard deviation, i.e., the variability of returns from the mean.测量标准差，即平均收益的变异性 It is an indicator of the actual price risk.

The realized volatility or actual volatility in the market is caused by two components- a continuous volatility component and a jump component, which influence the stock prices. Continuous volatility in a stock market is affected by the intra-day trading volumes. 股票市场的持续波动受日内(当天的)交易量的影响For example, a single high volume trade transaction can introduce a significant variation in the price of an instrument.

Analysts make use of high-frequency intraday data to determine measures of volatility at hourly/daily/weekly or monthly frequency. The data may then be utilized to forecast the volatility in returns.

Realized Volatility Formula

It is measured by calculating the standard deviation from the average price of an asset in a given time period. Since volatility is non-linear, realized variance is

first calculated by converting returns from a stock/asset to logarithmic values and
- Variance in daily returns of the underlying标的资产 is calculated as follows: $\small r_t = log(\frac{P_t}{P_{t-1}}) = log(P_t) - log(P_{t-1})$ This approach assumes the mean to be set to zero, considering the upside and downside trend in the movement of stock prices.
  - P= stock price
  - t= time period
measuring the standard deviation of log normal returns.
- Realized variance is calculated by computing the aggregate of returns over the time period defined $Realized\; Variance = \sum_{i=1}^{T} r_t^2$
  
  where = number of observations (monthly/ weekly/ daily returns). Typically, 20, 50, and 100-day returns are calculated.
- The formula of Realized volatility is the square root of realized variance.
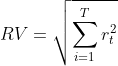  $RV = \sqrt{\sum_{i=1}^{T} r^2_t}$ Realized volatility is frequently used for daily volatility using the intraday returns.
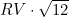- The results are then annualized. Realized variance is annualized by multiplying daily realized variance with a number of trading days/weeks/ months in a year.The square root of the annualized realized variance is the realized volatility $\small RV\cdot \sqrt{12}$ .

Examples of Realized Volatility

Example #1

For example, supposed realized volatility for two stocks with similar closing prices is calculated for 20, 50, and 100 days for stock and is annualized with values as follows:

Looking at the pattern of increasing volatility in the given time frame, it can be inferred that stock-1 has been trading with high variation in prices in recent times (i.e., 20 days), whereas stock-2 has been trading without any wild swings.

Advantages

It measures the actual performance of an asset in the past and helps to understand the stability of the asset based on its past performance.
It is an indicator of how an asset’s price has changed in the past and the time period in which it has undergone the change.
Higher the volatility, the higher the price risk associated with the stock, and therefore higher the premium attached to the stock因此与股票相关的溢价就越高。.
The realized volatility of the asset may be used to forecast future volatility, i.e., implied volatility of the asset. While entering into transactions with complex financial products such as derivatives, options, etc., the premiums are determined based on the volatility of the underlying and influences the prices of these products.
It is the starting point for option pricing.
Realized volatility is measured based on statistical methods and is, therefore, a reliable indicator of the volatility in asset value.

Disadvantages

It is a measure of historical volatility and is therefore not forward-looking. It does not factor in any major “shocks” in the market that may arise in the future, which may affect the value of the underlying.

Limitation

The volume of data used influences the end results during the calculation of realized volatility. At least 20 observations are statistically required to calculate a valid value of realized volatility. Therefore, realized volatility is better used to measure longer-term price risk in the market (~ 1 month or more).
Realized volatility calculations are directionless. i.e., it factors in upward and downward trends in price movements它会影响价格走势的上升和下降趋势。.
It is assumed that asset prices reflect all available information while measuring volatility.

Important Points

In order to calculate the downside risk associated with a stock, the measurement of realized volatility may be restricted to downside price movements.
An increase in realized volatility of a stock over a time period would imply a significant change in the inherent value of the stock owning to external/internal factors.
An increase in volatility implies a higher premium on option prices. The value of a stock can be inferred by comparing the realized volatility and estimated future volatility (implied volatility) of the options.可以通过比较期权的已实现波动率和估计的未来波动率（隐含波动率）来推断股票的价值。
Comparing the volatility of a stock with the benchmark index helps determine the stability of stock将股票的波动性与基准指数进行比较有助于确定股票的稳定性: the lower the volatility, the more predictable the price of the asset.
A decrease in the realized volatility of a stock over a time period would indicate the stabilization of the stock.

Realized volatility measures help to quantify the inherent price risk arising out of volume fluctuations and external factors of a stock based on its historical performance. Combined with implied volatility, it also helps determine option prices based on the volatility in the underlying stock.

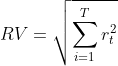$RV = \sqrt{\sum_{i=1}^{T} r^2_t}$ Realized volatility is frequently used for daily volatility using the intraday returns.

The steps we need to take are as follows:

Download the data and calculate the log returns.
Calculate the realized volatility over the months.
Annualize the values by multiplying by 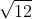$\sqrt{12}$ , as we are converting from monthly values.

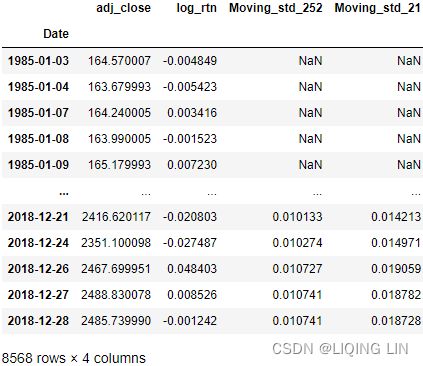
We assume you have followed the instructions from earlier recipes and have a DataFrame called df with a single log_rtn column and timestamps as the index.
converting returns from a stock/asset to logarithmic values $\small r_t = log(\frac{P_t}{P_{t-1}}) = log(P_t) - log(P_{t-1})$

import pandas as pd
import numpy as np
import yfinance as yf

# progress=True : Progress will show a progress bar.
# auto_adjust will overwrite the Close
# Adjust all OHLC automatically? Default is False
df = yf.download( 'AAPL',
                  start='2000-01-01',
                  end='2010-12-31',
                  auto_adjust=False,
                  progress=False
                )

# keep only the adjusted close price
df = df.loc[:, ['Adj Close']]
df.rename( columns={'Adj Close':'adj_close'},
           inplace=True
         )

# converting returns from a stock/asset to logarithmic values
df['log_rtn'] = np.log( df['adj_close']/df['adj_close'].shift(1) )

df.drop('adj_close', axis=1, inplace=True)
df.dropna( axis=0, inplace=True )
df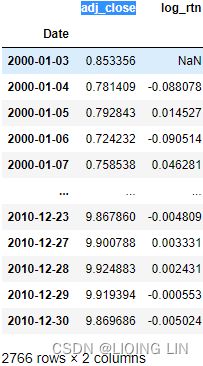

==>
2. Define the function for calculating the realized volatility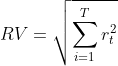 $RV = \sqrt{\sum_{i=1}^{T} r^2_t}$ and
3. Calculate the monthly realized volatility:

import pandas as pd

def realized_volatility(x):
    return np.sqrt( np.sum(x**2) # Realized variance for each month
                  ) # Realized volatility

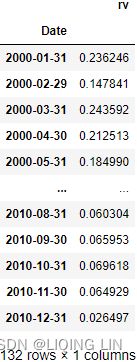
df_rv = df.groupby( pd.Grouper( freq='M') ).apply(realized_volatility)
df_rv.rename( columns={'log_rtn':'rv'},
              inplace=True
            )
df_rv

==>==>

4.Annualize the values $\small RV \cdot \sqrt{12}$ :

df_rv.rv = df_rv.rv * np.sqrt(12)
df_rv

5. Plot the results:

import matplotlib.pyplot as plt
plt.style.use('seaborn')

fig, ax = plt.subplots(2, 1, sharex=True, figsize=(10,10))

ax[0].plot(df)
ax[0].set_title('daily log return(adjust_close)')
ax[1].plot( df_rv )
ax[1].set_title('realized volatility')

plt.show()

We can see that the spikes(it can be inferred that stock has been trading with high variation in prices in that time point) in the realized volatility coincide with some extreme log-returns (which might be outliers).

Normally, we could use the resample method of a pandas DataFrame. Supposing we wanted to calculate the average monthly return, we could run df.log_rtn.resample(' M' ).mean().

For the resample method, we can use any built-in aggregate functions of pandas, such as mean, sum, min, and max. However, our case is a bit more complex, so we defined a helper function called realized_volatility, and replicated the behavior of resample by using a combination of groupby, Grouper, and apply.
###################

###################

Identifying outliers

While working with any kind of data, we often encounter observations that are significantly different from the majority, that is, outliers. They can be a result of a wrong tick (price), something major happening on the financial markets金融市场上发生的重大事件, an error in the data processing pipeline, and so on. Many machine learning algorithms and statistical approaches can be influenced by outliers, leading to incorrect/biased results. That is why we should handle the outliers before creating any models.

Execute the following steps to detect outliers using the 3σ( $\small R_t \notin [sma - 3\sqrt{\sigma}, sma + 3\sqrt{\sigma}]$ ) approach, and mark them on a plot.

import pandas as pd
import yfinance as yf

df = yf.download( 'AAPL',
                  start='2000-01-01',
                  end='2010-12-31',
                  progress=False
                )
df = df.loc[:, ['Adj Close']] # keep only the adjusted close price
df.rename( columns={'Adj Close':'adj_close'},
           inplace=True
         )
df['simple_rtn'] = df.adj_close.pct_change()
df

<== $\small R_t = \frac{P_t - P_{t-1}}{P_{t-1}} = \frac{P_t}{P_{t-1}} - 1$

Calculate the rolling mean and standard deviation:

Simple moving average

Simple moving average, which we will refer to as SMA, is a basic technical analysis indicator. The simple moving average, as you may have guessed from its name, is computed by adding up the price of an instrument over a certain period of time divided by the number of time periods. It is basically the price average over a certain time period, with equal weight being used for each price. The time period over which it is averaged is often referred to as the lookback period or history. Let's have a look at the following formula of the simple moving average:
Here, the following applies:

$\small P_i$ : Price at time period i
$\small N$ : Number of prices added together or the number of time periods(lookback periods)

#########rolling window https://blog.csdn.net/Linli522362242/article/details/122955700

There are exactly 252 trading days in 2021. January and February have the fewest (19), and March the most (23), with an average of 21 per month, or 63 per quarter.

Out of a possible 365 days, 104 days(365/7=52*2=104) are weekend days (Saturday and Sunday) when the stock exchanges are closed. Seven of the nine holidays which close the exchanges fall on weekdays, with Independence Day being observed on Monday, July 5, and Christmas on Friday, December 24. There is one shortened trading session on Friday, November 26 (the day after Thanksgiving Day). ==> 365-104-7-2=252
########

Standard deviation

Standard deviation, which will be referred to as STDEV, is a basic measure of price volatility that is used in combination with a lot of other technical analysis indicators to improve them. We'll explore that in greater detail in this section.

Standard deviation is a standard measure that is computed by measuring the squared deviation of individual prices from the mean price, and then finding the average of all those squared deviation values. This value is known as variance, and the standard deviation is obtained by taking the square root of the variance.
Larger STDEVs are

a mark of more volatile markets市场波动较大的标志 or
larger expected price moves,
so trading strategies need to factor that increased volatility into risk estimates and other trading behavior.

To compute standard deviation, first we compute the variance:
Then, standard deviation is simply the square root of the variance:

SMA : Simple moving average over n time periods.

# Calculate the rolling mean and standard deviation:
# 21 : the average number of trading days in a month 
df_rolling = df[['simple_rtn']].rolling( window=21 )\
                                .agg(['mean',# SMA
                                      'std'
                                     ])
# df_rolling.columns
#      MultiIndex([('simple_rtn', 'mean'),
#                  ('simple_rtn',  'std')
#                 ],)
df_rolling.columns = df_rolling.columns.droplevel()
# droplevel()
#    Return Series/DataFrame with requested index / column level(s) removed
df_rolling

df df_rolling df_rolling

==>==>

2. Join the rolling metrics to the original data:

df_outliers = df.join(df_rolling, how='left')
df_outliers[:25]

<==rolling( window=21 )

3. Define a function for detecting outliers(using the 3σ approach $\small R_t \notin [sma - 3\sqrt{\sigma}, sma + 3\sqrt{\sigma}]$ ):
we defined a function that

returns 1 if the observation is considered an outlier, according to the 3σ rule (we parametrized the number of standard deviations),
and 0 otherwise.

The condition for a given observation x to be qualified as an outlier is x > μ + 3σ or x < μ - 3σ.

def identify_outliers( row, n_sigmas = 3 ):
    '''
    Function for identifying the outliers using the 3 sigma rule. 
    The row must contain the following columns/indices: simple_rtn, mean, std.
    
    Parameters
    ----------
    row : pd.Series
        A row of a pd.DataFrame, over which the function can be applied.
    n_sigmas : int
        The number of standard deviations above/below the mean - used for detecting outliers
        
    Returns
    -------
    0/1 : int
        An integer with 1 indicating an outlier and 0 otherwise.
    '''    
    x = row['simple_rtn']
    mu = row['mean']
    sigma = row['std']
    
    if( (x < mu - n_sigmas*sigma) | (x > mu + n_sigmas*sigma) ):
        return 1
    else:
        return 0

4. Identify the outliers and extract their values for later use:

df_outliers['outlier'] = df_outliers.apply( identify_outliers,
                                            axis=1 # for each row
                                          )
outliers = df_outliers.loc[ df_outliers['outlier']==1,
                            ['simple_rtn']
                          ]
outliers

5. Plot the results:

fig = plt.figure( figsize=(10,8) )

plt.plot( df_outliers.index, df_outliers.simple_rtn,
          color='blue', label='Normal'
        )
plt.scatter( outliers.index, outliers.simple_rtn,
             color='red', label='Anomaly'
           )
plt.title("Apple's stock returns")
plt.legend( loc='lower right')
plt.show()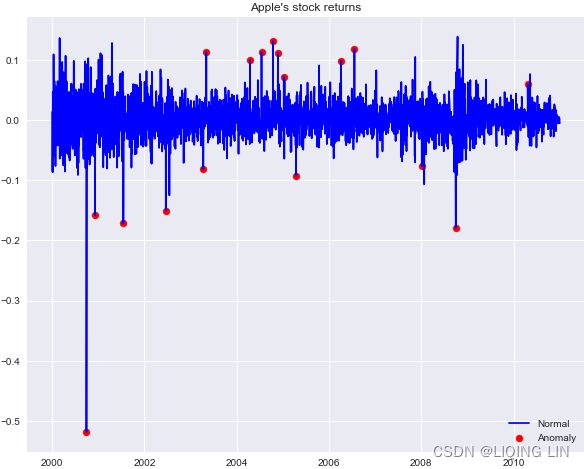

In the plot, we can observe outliers marked with a red dot. One thing to notice is that when there are two large returns in the vicinity, the algorithm identifies the first one as an outlier and the second one as a regular observation. This might be due to the fact that the first outlier enters the rolling window and affects the moving average/standard deviation.

In real-life cases, we should not only identify the outliers, but also treat them, for example, by capping them at限制在 the maximum/minimum acceptable value, replacing them by interpolated values, or by following any of the other possible approaches.

There are many different methods of identifying outliers in a time series, for example, using Isolation Forest, Hampel Filter, Support Vector Machines, and z-score (which is similar to the presented approach).

In the 3σ approach, for each time point, we calculated the moving average (μ) and standard deviation (σ) using the last 21 days (not including that day since we missing the first day trading data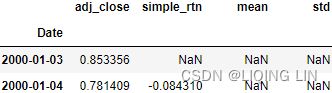). We used 21 as this is the average number of trading days in a month, and we work with daily data. However, we can choose different value, and then the moving average will react faster/slower to changes. We can also use (exponentially) weighted moving average if we find it more meaningful in our particular case. https://blog.csdn.net/Linli522362242/article/details/121406833

Investigating stylized facts of asset returns

Stylized程式化的,按固定格式的 facts are statistical properties that appear to be present in many empirical/ɪmˈpɪrɪk(ə)l/经验主义的,以经验为依据的 asset returns (across time and markets). It is important to be aware of them because when we are building models that are supposed to represent asset price dynamics, the models must be able to capture/replicate these properties.

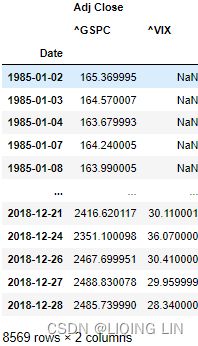
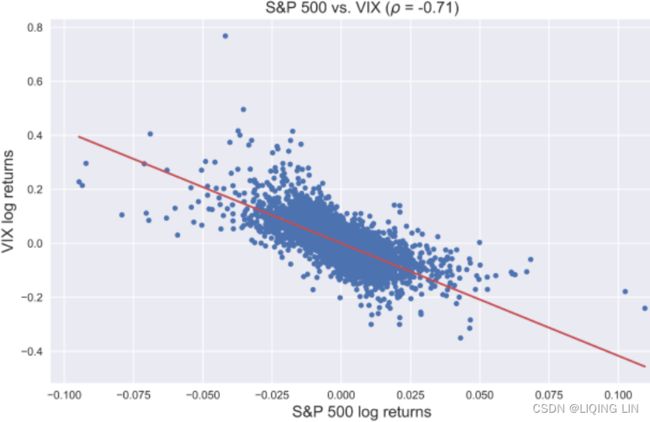
In the following recipes, we investigate the five stylized facts using an example of daily S&P 500 returns from the years 1985 to 2018.

We download the S&P 500 prices from Yahoo Finance (following the approach in the Getting data from Yahoo Finance recipe) and calculate returns as in the Converting prices to returns recipe.

Fact1:Non-Gaussian distribution of returns回报的非高斯(正态)分布

The name of the fact (Non-Gaussian distribution of returns) is pretty much selfexplanatory. It was observed in the literature that (daily) asset returns exhibit the following:

Negative skewness (third moment): Large negative returns occur more frequently than large positive ones.
Excess kurtosis (fourth moment) : Large (and small) returns occur more often than expected.

Note:
The pandas implementation of kurtosis is the one that literature refers to as excess kurtosis or Fisher's kurtosis费舍尔峰度. Using this metric, the excess kurtosis of a Gaussian distribution(or called normal distribution) is 0, while the standard kurtosis is 3. This is not to be confused with the name of the stylized fact's excess kurtosis, which simply means kurtosis higher than that of normal distribution(or called Gaussian distribution)它仅表示峰度高于正态分布的峰度( excess kurtosis=Kurtosis-3=0 ).

Samples from a normal distribution have
- an expected skewness of 0 and
- an expected excess kurtosis of 0 (which is the same as a kurtosis of 3).
  The normal distribution has standard Kurtosis=3. The measure ( excess kurtosis=Kurtosis-3=0 ) is known ast the "Excess Kurtosis", i.e: $\large K = \frac{\hat{u}_4}{\hat{\sigma}^4} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2)^{2}}-3$
- Jarque-Bera 检验使用正态的这两个（统计）属性分布

In social sciences, especially economics, a stylized fact is a simplified presentation of an empirical finding.[1] Stylized facts are broad tendencies that aim to summarize the data, offering essential truths while ignoring individual details.

A prominent example of a stylized fact is: "Education significantly raises lifetime income." Another stylized fact in economics is: "In advanced economies, real GDP growth fluctuates in a recurrent but irregular fashion".

However, scrutiny to detail will often produce counterexamples对细节的审查往往会产生反例。. In the case given above, holding a PhD may lower lifetime income, because of the years of lost earnings it implies and because many PhD holders enter academia instead of higher-paid fields. Nonetheless, broadly speaking, people with more education tend to earn more, so the above example is true in the sense of a stylized fact.

Stylized facts are widely used in economics, in particular to motivate the construction of a model and/or to validate it. Examples are:

Stock returns are uncorrelated and not easily forecastable.[6]
Yield curves tend to move in parallel.
Education is positively correlated to lifetime earnings
Inventory behavior of firms: “the variance of production exceeds the variance of sales”

Run the following steps to investigate the existence of this first fact by plotting the histogram of returns and a Q-Q plot.

import pandas as pd
import yfinance as yf

df = yf.download( '^GSPC',
                  start='1985-01-01',
                  end='2018-12-31',
                  progress=False
                )
df = df[['Adj Close']].rename( columns={'Adj Close':'adj_close'} )
df['log_rtn'] = np.log( df.adj_close/df.adj_close.shift(1) )

df = df[['adj_close', 'log_rtn']].dropna( how='any' )
df

##################################################################

the binomial distribution

概率密度函数(Probability Density Function (PDF) 连续性数据) where n is the number of trials, p is the probability of success, and N is the number of successes.
概率质量函数(Probability Mass Function, PMF,离散型数据)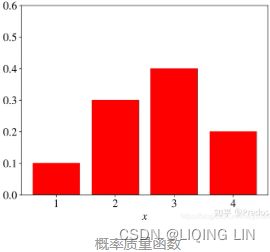是离散随机变量在各特定取值上的概率
概率质量函数PMF是对离散随机变量定义的，本⾝代表该值的概率；
概率密度函数PDF是对连续随机变量定义的，本⾝不是概率，只有对连续随机变量的概率密度函数PDF在某区间内进⾏积分后才是概率
The cumulative distribution function (cdf) or distribution function of a random variable X of the continuous type, defined in terms of the pdf of X, is given by
Here, again, F(x) accumulates (or, more simply, cumulates) all of the probability less than or equal to x. From the fundamental theorem of calculus, we have, for x values
for which the derivative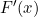 $\small F'(x)$ exists, 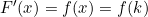$\small F'(x) = f(x) = f(k)$ and we call 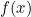$\small f(x)$ the Probability Density Function (PDF) of X

seaborn.distplot can help us to process the data into bins and show us a histogram as a result.

The seaborn.distplot function expects either pandas Series, single-dimensional numpy.array, or a Python list as input. Then, it determines the size(width) of the bins according to the Freedman-Diaconis rule(the size of the bins =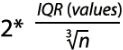 , the number of bins =, Interquartile range( IQR = Q3-Q1 ), Freedman-Diaconisf方法偏向适用于长尾分布的数据，因为其对数据中的离群值不敏感。x表示事例的数值分布情况), and finally it fits(curve) a kernel density estimate (KDE) over the histogram.

KDE is a non-parametric method used to estimate the distribution of a variable. We can also supply a parametric distribution, such as beta, gamma, or normal distribution, to the fit argument.https://blog.csdn.net/Linli522362242/article/details/93617948

##############
1. Calculate the normal Probability Density Function (PDF) using the mean and standard deviation of the observed returns:

import scipy.stats as scs

r_range = np.linspace( min(df.log_rtn), max(df.log_rtn),
                       num=1000
                     )
mu = df.log_rtn.mean()
sigma = df.log_rtn.std()

# scipy.stats.norm ： A normal continuous random variable.
# The location (loc) keyword specifies the mean.
# The scale (scale) keyword specifies the standard deviation
norm_pdf = scs.norm.pdf( r_range, loc=mu, scale=sigma )

2. Plot the histogram and the Q-Q plot:

import seaborn as sns
import statsmodels.api as sm
import matplotlib.pyplot as plt

# https://blog.csdn.net/Linli522362242/article/details/93617948
sns.set(font_scale=1.)
# sns.set_style('ticks') # white, dark, whitegrid, darkgrid, ticks

fig, ax = plt.subplots( 1,2, figsize=(12,8) )

# histogram
# sns. displot()
# norm_hist:若为True, 则直方图高度显示密度而非计数(含有kde图像中默认为True)
sns.distplot( df.log_rtn, kde=False, norm_hist=True, ax=ax[0], )
ax[0].plot( r_range, norm_pdf, 
            'g', lw=2, label=f'N({mu:.2f}, {sigma**2 : .4f})',
          )
ax[0].legend(loc='upper left')
ax[0].set_title( 'Distribution of S&P 500 returns', fontsize=16 )

# Q-Q plot
qq = sm.qqplot( df.log_rtn.values, line='s', ax=ax[1],
                markerfacecolor='b',
                # markeredgecolor='k'
                # alpha=0.3
              )
# sm.qqline( qq.axes[1], line='45', #If line is not 45, x and y cannot be None.
#            fmt='y--') #fmt = '[marker][line][color]'
ax[1].get_lines()[1].set_color('red')
ax[1].get_lines()[1].set_linewidth(3.0)
ax[1].set_title('Q-Q plot', fontsize=16)

plt.show()

Histogram of returns

The first step of investigating this fact was to plot a histogram visualizing the distribution of returns. To do so, we used sns.distplot while setting kde=False (which does not use the Gaussian kernel density estimate) and norm_hist=True (this plot shows density instead of the count).

To see the difference between our histogram and Gaussian distribution(or called Normal distribution), we superimposed a line representing the PDF of the Gaussian distribution with the mean(mu = df.log_rtn.mean()) and standard deviation(sigma = df.log_rtn.std()) coming from the considered return series.

First, we specified the range over which we calculated the PDF by using np.linspace (we set the number of points to 1,000, generally the more points the smoother the line) and then calculated the PDF using scs.norm.pdf . The default arguments correspond to the standard normal distribution, that is, with zero mean and unit variance即0均值(loc default=1)和单位方差(scale default=1). That is why we specified the loc and scale arguments as the sample mean and standard deviation, respectively.

To verify the existence of the previously mentioned patterns, we should look at the following:

Negative skewness: The left tail of the distribution is longer, while the mass of the distribution is concentrated on the right side of the distribution.而分布的质量集中在分布的右侧。(Large negative returns occur more frequently than large positive ones.)
Excess kurtosis: Fat-tailed and peaked distribution(leptokurtic distributions are sometimes characterized as "concentrated toward the mean,"(“向均值集中”)). Large(Massive) and (small) returns occur more often than expected大量的小额回报的发生频率比预期的要高.

The second point is easier to observe on our plot, as there is a clear peak over the PDF and we see more mass in the tails.

Q-Q plot

After inspecting the histogram, we looked at the Q-Q (quantile-quantile) plot, on which we compared two distributions (theoretical and observed) by plotting their quantiles against each other. In our case,

the theoretical distribution is Gaussian (Normal) and
the observed one comes from the S&P 500 returns.

To obtain the plot, we used the sm.qqplot function. If the empirical distribution is Normal, then the vast majority of the points will lie on the red line 如果经验分布是正态分布，那么绝大多数点将位于红线上. However, we see that this is not the case, as points on the left side of the plot are more negative (that is, lower empirical quantiles are smaller) than expected in the case of the Gaussian distribution, as indicated by the line. This means that the left tail of the returns distribution is heavier than that of the Gaussian distribution. Analogical conclusions can be drawn about the right tail, which is heavier than under normality.

if `distplot` is deprecated(solution):

import seaborn as sns
import statsmodels.api as sm
import matplotlib.pyplot as plt

sns.set(font_scale=1.1)
#sns.set() # Reset all previous theme settings to default
# sns.set( context="notebook",
#          style="darkgrid",
#          font_scale=1.2,      # increase the font scale#
#          rc={ #'grid.color': '0.6',
#               'axes.labelcolor':'darkblue',
#               #"lines.linewidth": 2.5, # increase the line width of the KDE plot
#             }
#        )

fig, ax = plt.subplots( 1,2, figsize=(12,8) )

# histogram
# sns. displot()
# norm_hist:若为True, 则直方图高度显示密度而非计数(含有kde图像中默认为True)
sns.histplot( df.log_rtn,
              kde=False,
              stat='density', #norm_hist=True,
              ax=ax[0],
              bins=50,
              color='b'
            )
ax[0].plot( r_range, norm_pdf, 
            'g', lw=2, label=f'N({mu:.2f}, {sigma**2 : .4f})',
          )
# ax[0].fig.legend(loc='upper left')
ax[0].set_title( 'Distribution of S&P 500 returns', fontsize=16 )

# Q-Q plot
qq = sm.qqplot( df.log_rtn.values, line='s', ax=ax[1],
                markerfacecolor='b',
                # markeredgecolor='k'
                # alpha=0.3
              )
# sm.qqline( qq.axes[1], line='45', # If line is not 45, x and y cannot be None.
#            fmt='y--') #fmt = '[marker][line][color]'
ax[1].get_lines()[1].set_color('red')
ax[1].get_lines()[1].set_linewidth(3.0)
ax[1].set_title('Q-Q plot', fontsize=16)

plt.subplots_adjust(wspace=0.3)
plt.show()

We can use the histogram (showing the shape of the distribution) and the Q-Q plot to assess the normality of the log returns评估对数回报的正态性. Additionally, we can print the summary statistics:

Perform the Jarque-Bera goodness of fit test on sample data.

The Jarque-Bera test tests whether the sample data has the skewness and kurtosis matching a normal distribution.

Note that this test only works for a large enough number of data samples (>2000) as the test statistic asymptotically has a Chi-squared distribution with 2 degrees of freedom.

# import scipy.stats as scs
# df['log_rtn'] = np.log( df.adj_close/df.adj_close.shift(1) )
jb_test = scs.jarque_bera( df.log_rtn.values )

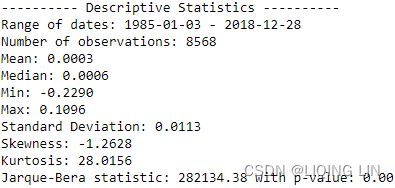
print( '---------- Descriptive Statistics ----------' )
print( 'Range of dates:', min(df.index.date), '-', max(df.index.date) )
print( 'Number of observations:', df.shape[0] )
print( f'Mean: {df.log_rtn.mean():.4f}' )
print( f'Median: {df.log_rtn.median():.4f}' )
print( f'Min: {df.log_rtn.min():.4f}' )
print( f'Max: {df.log_rtn.max():.4f}' )
print( f'Standard Deviation: {df.log_rtn.std():.4f}' )
print( f'Skewness: {df.log_rtn.skew():.4f}' )
print( f'Kurtosis: {df.log_rtn.kurtosis():.4f}' )
print( f'Jarque-Bera statistic: {jb_test[0]:.2f} with p-value: {jb_test[1]:.2f}')

If the data comes from a normal distribution, the JB statistic asymptotically has a chi-squared distribution with two degrees of freedomJB 统计量渐近具有自由度为2的卡方分布, so the statistic can be used to test the hypothesis that the data are from a normal distribution.

https://www.itl.nist.gov/div898/handbook/eda/section3/eda3674.htm

We immediately see that the returns exhibit negative skewness and excess kurtosis. We also ran the Jarque-Bera test ( scs.jarque_bera ) to verify that returns do not follow a Gaussian distribution. With a p-value of zero, we reject the null hypothesis that sample data has skewness and kurtosis matching those of a Gaussian distribution(called Normal distribution).

first fact $JB_{test} > 5.991_{\alpha=0.05}$

At 5% significant level(α = 0.05), we reject the null hypothesis that the log-return is normally distributed(OR $\large H_0 : S_{expected}= 0, K_{expected \; excess} =0 \;OR\; K=3$ ).
By looking at the metrics such as the mean, standard deviation, skewness, and kurtosis we can infer that they deviate from what we would expect under normality. Additionally, the Jarque-Bera normality test gives us reason to reject the null hypothesis stating that the distribution is normal at the 99% confidence level(α = 0.01).

Jarque–Bera test : can give us reason to reject the null hypothesis

In statistics, the Jarque–Bera test is a goodness-of-fit test拟合优度检验 of whether sample data have the skewness and kurtosis matching a normal distribution. The test statistic is always nonnegative. If it is far from zero, it signals the data do not have a normal distribution.

The test statistic JB is defined as $JB = \frac{n}{6} ( S^2 + \frac{1}{4}(K-3)^2 )$
Skewness is a function of data, i.e. a random variable, Kurtosis is a function of data, i.e. a random variable, so JB $JB = \frac{n}{6} ( S^2 + \frac{1}{4}(K-3)^2 )$ is is a random variable, and follows what distribution?
where

n is the number of observations (or degrees of freedom in general);
S is the sample skewness: $\large S = \frac{\hat{u}_3}{\hat{\sigma}^3} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^3}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2)^{3/2}}$
Zero skewness implies asymmetric distribution非对称分布 (the Normal, t-distribution)
Skewness is a function of data, i.e. a random variable
K is the sample kurtosis : $\large K = \frac{\hat{u}_4}{\hat{\sigma}^4} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2)^{2}}$
Kurtosis is a function of data, i.e. a random variable
- where $\large \hat{u}_3$ and $\large \hat{u}_4$ are the estimates of third and fourth central moments,三阶中心矩和四阶中心矩的估计值 respectively,
- $\large \bar{x}$ is the sample mean, and
- $\large \hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2$ is the estimate of the second central moment二阶中心矩（即方差）的估计值, the variance.

If the data comes from a normal distribution, the JB statistic asymptotically has a chi-squared distribution with two degrees of freedomJB 统计量渐近具有自由度为2的卡方分布, so the statistic can be used to test the hypothesis that the data are from a normal distribution.

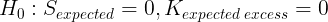
The null hypothesis is a joint hypothesis of the skewness being zero and the excess kurtosis being zero. $\large H_0 : S_{expected}= 0, K_{expected\; excess} =0$
Samples from a normal distribution have
- an expected skewness of 0 and
- an expected excess kurtosis of 0 (which is the same as a kurtosis of 3).
  The normal distribution has Kurtosis=3. The measure ( excess kurtosis= Kurtosis-3 =0) is known ast the "Excess Kurtosis", i.e: $\large K = \frac{\hat{u}_4}{\hat{\sigma}^4} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2)^{2}}-3$
- Jarque-Bera 检验使用正态的这两个（统计）属性分布
As the definition of JB shows, any deviation from this increases the JB statistic.
The Jarque-Bera test tests the hypothesis
H0: Data is normal
H1: Data is NOT norma

The Jarque-Bera test — Example

Hypotheses:
H0: The error term is normally distributed,
H1: The error term is not normally distributed
Significance level: α = 0.05 and How to do a Jarque-Bera test in practice:
1. 1 Calculate the skewness in the sample. $\large S = \frac{\hat{u}_3}{\hat{\sigma}^3} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^3}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2)^{3/2}}$
2. 2 Calculate the kurtosis in the sample. $\large K = \frac{\hat{u}_4}{\hat{\sigma}^4} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2)^{2}}$
3. Assumptions n large, Calculate the Jarque-Bera test statistic : $JB = \frac{n}{6} ( S^2 + \frac{1}{4}(K-3)^2 )$
  which under the null( asymptoically ) follows a a chisquare distribution with 2 df
  JB统计量近似服从自由度为2的卡方分布
4. 4 Compare the Jarque-Bera test statistic with the critical values in the chi-square table, 2 df.
  Distribution under the null rejection rule: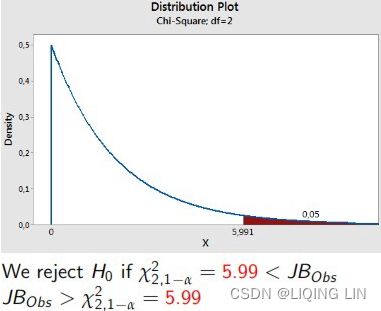
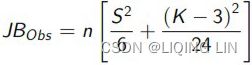
5. At 5% significant level(α = 0.05), we reject the null of that the disturbance term is normally distributed.(The error term is not normally distributed)

For small samples the chi-squared approximation is overly sensitive, often rejecting the null hypothesis when it is true. Furthermore, the distribution of p-values departs from a uniform distribution and becomes a right-skewed unimodal distribution, especially for small p-values. This leads to a large Type I error rate(Type I error(FP): Rejecting a null hypothesis when it is true, (OR is true, but we reject it by mistake. Because we mistakenly think is False, ###wrongly reject
P=target class(the null hypothesis=False, Reject) https://blog.csdn.net/Linli522362242/article/details/125662545)
). The table below shows some p-values approximated by a chi-squared distribution that differ from their true alpha levels for small samples.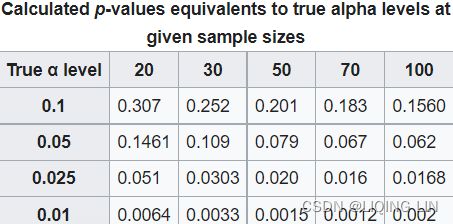

Skewness(偏度)

用来描述数据分布的对称性Skewness measures the degree of symmetry in the distribution. $\large S = \frac{\hat{u}_3}{\hat{\sigma}^3} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^3}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2)^{3/2}}$

正态分布的偏度为0。
Zero skewness implies asymmetric distribution非对称分布 (the Normal, t-distribution)
计算数据样本的偏度，
当偏度<0时，称为负偏，数据出现左侧长尾；
Negative skewness means that the distribution has a long left tail, its skewed to the left.
当偏度>0时，称为正偏，数据出现右侧长尾；
Positive skewness means that the distribution has a long right tail, it's skewed to the right.
当偏度为0时，表示数据相对均匀的分布在平均值两侧，不一定是绝对的对称分布，此时要与正态分布偏度为0的情况进行区分。
当偏度绝对值过大时，长尾的一侧出现极端值的可能性较高。

Kurtosis measures how much of a probability distribution is centered around the middle (mean) vs. the tails峰度测量有多少概率分布集中在中间（平均值）与尾部.Positive or negative excess kurtosis will then change the shape of the distribution, accordingly. 正或负的超峰度将相应地改变分布的形状。
Skewness instead measures the relative symmetry of a distribution around the mean偏度测量平均值周围分布的相对对称性。.

Kurtosis(峰度)

用来描述数据分布陡峭或是平滑的情况。 $\large K = \frac{\hat{u}_4}{\hat{\sigma}^4} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2)^{2}}$
Kurtosis explains how often observations in some data set fall in the tails vs. the center of a probability distribution.峰度解释了某些数据集中的观测值落在概率分布的尾部与中心的频率 In finance and investing, excess kurtosis is interpreted as a type of risk, known as "tail risk,"尾部风险 or the chance of a loss occurring due to a rare event或由概率分布预测的由于罕见事件而发生损失的可能性, as predicted by a probability distribution. If such events turn out to be more common than predicted by a distribution, the tails are said to be "fat." Tail events have had experts questions the true probability distribution of returns for investable assets - and now many believe that the normal distribution is not a correct template.尾部事件让专家质疑可投资资产回报的真实概率分布——现在许多人认为正态分布不是一个正确的模板。

正态分布的峰度为3，
The normal distribution has Kurtosis=3. The measure ( Kurtosis-3 ) is known ast the "Excess Kurtosis", i.e: $\large K = \frac{\hat{u}_4}{\hat{\sigma}^4} = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^4}{(\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar{x})^2)^{2}}-3$
Excess kurtosis compares the kurtosis coefficient with that of a normal distribution.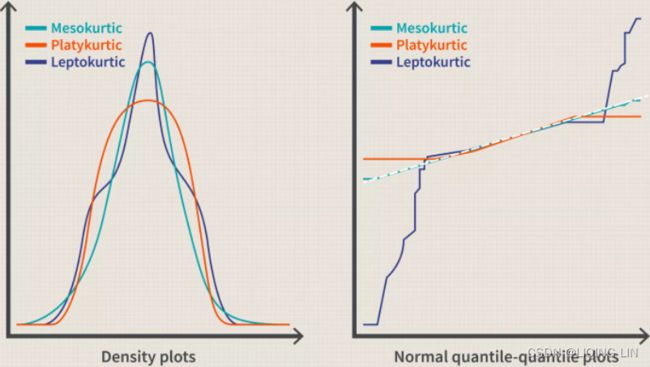
A distribution with kurtosis=3 is said to be mesokurtic中峰分布(常峰态分布).
This distribution has a kurtosis statistic similar to that of the normal distribution, meaning the extreme value characteristic of the distribution is similar to that of a normal distribution.
A distribution with kurtosis>3 is said to be leptokurtic/ ˌleptəˈkərtɪk /尖峰态分布 or fat-tailed胖尾.
Any distribution that is leptokurtic displays greater kurtosis than a mesokurtic distribution. Characteristics of this distribution is one with long tails (outliers.) The prefix of "lepto-" means "skinny," making the shape of a leptokurtic distribution easier to remember. The "skinniness" of a leptokurtic distribution is a consequence of the outliers, which stretch the horizontal axis of the histogram graph, making the bulk of the data appear in a narrow ("skinny") vertical range.细峰分布的“瘦”是异常值的结果，异常值拉伸直方图的水平轴，使大部分数据出现在狭窄（“瘦”）的垂直范围内。
Thus leptokurtic distributions are sometimes characterized as "concentrated toward the mean,"(“向均值集中”) but the more relevant issue (especially for investors) is there are occasional extreme outliers that cause this "concentration" appearance. Examples of leptokurtic distributions are the T-distributions with small degrees of freedom.
Platykurtic (kurtosis < 3.0)
The final type of distribution is a platykurtic distribution. These types of distributions have short tails (paucity/ˈpɔːsəti/ of outliers缺乏异常值.) The prefix of "platy-" means "broad," and it is meant to describe a short and broad-looking peak短而宽的峰值, but this is an historical error. Uniform distributions (1.3.6.6.2. Uniform Distribution orhttps://en.wikipedia.org/wiki/Continuous_uniform_distribution )are platykurtic and have broad peaks, but the beta (.5,1) distribution is also platykurtic and has an infinitely pointy peak.
峰度越大，代表分布越陡峭，尾部越厚；
如果峰度大于三，峰的形状比较尖，比正态分布峰要陡峭。反之亦然
峰度越小，分布越平滑。
很多情况下，为方便计算，将峰度值－3 ( Kurtosis-3 )，因此正态分布的峰度变为0，方便比较。
在方差相同(或者相同的标准差)的情况下，峰度(系数)越大，分布就可能有更多的极端值，那么其余值必然要更加集中在众数周围，其分布必然就更加陡峭#https://blog.csdn.net/Linli522362242/article/details/99728616

Fact2: Volatility clustering

Run the following code to investigate this second fact by plotting the log returns series.

1. Visualize the log returns series:

df.log_rtn.plot( title='Daily S&P 500 returns', figsize=(10,6) )

plt.show()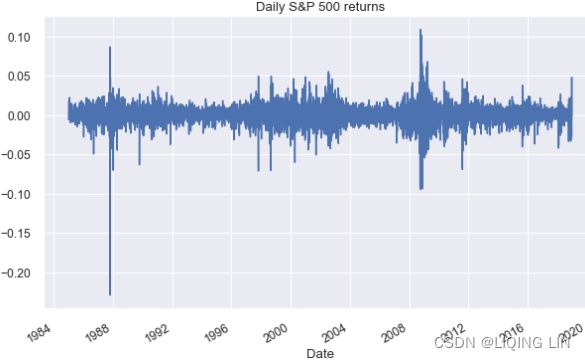

We can observe clear clusters of volatility—periods of higher positive and negative returns.

The first thing we should be aware of when investigating stylized facts is the volatility clustering—periods of high returns alternating with交替出现 periods of low returns, suggesting that volatility is not constant. To quickly investigate this fact, we plot the returns using the plot method of a pandas DataFrame.

# Displaying rolling statistics
def plot_rolling_statistics_ts( ts, titletext, ytext, window_size=12 ):
    ts.plot( color='red', label='Original', lw=0.5 )
    ts.rolling( window_size ).mean().plot( color='blue', label='Rolling Mean' )
    ts.rolling( window_size ).std().plot( color='black', label='Rolling Std' )
    
    plt.legend( loc='best' )
    plt.ylabel( ytext )
    plt.xlabel( 'Date')
    plt.setp( plt.gca().get_xticklabels(), rotation=30, horizontalalignment='right' )
    plt.title( titletext )
    plt.show( block=False )

# df['log_rtn'] = np.log( df.adj_close/df.adj_close.shift(1) )
#                          the daily historical log returns
plot_rolling_statistics_ts( df.log_rtn, 
                           ' Daily S&P 500 returns rolling mean and standard deviation',
                           'Daily prices',
                          )

The intuition behind the test is as follows. If the series y is stationary (or trend-stationary, e.g. Daily S&P 500 log-return ), then it has a tendency to return to a constant (or deterministically trending确定性趋势) mean. Therefore, large values will tend to be followed by smaller values (negative changes), and small values by larger values (positive changes).

红线一直围绕均值波动。而均值不随时间变化（其实方差(标准差)也不随时间变化

A stationary time series is one whose statistical properties, such as mean, variance, and autocorrelation, are constant over time.https://blog.csdn.net/Linli522362242/article/details/126113926

It looks the daily S&P 500 log returns has no trend, seasonality or cyclic behaviour(In general, the average length of cycles is longer than the length of a seasonal pattern, and the magnitudes of cycles tend to be more variable than the magnitudes of seasonal patterns.). There are random fluctuations which do not appear to be very predictable, and no strong patterns that would help with developing a forecasting model.

Stationary process: A process that generates a stationary series of observations.
Trend stationary: A process that does not exhibit a trend.
Seasonal stationary: A process that does not exhibit seasonality.
Strictly stationary: Also known as strongly stationary. A process whose unconditional joint probability distribution of random variables does not change when shifted in time (or along the x axis)随机变量的无条件联合概率分布在随时间（或沿 x 轴）移动时不会改变.
Weakly stationary: Also known as covariance-stationary, or second-order stationary. A process whose mean, variance, and correlation of random variables doesn't change when shifted in time.

Making a time series stationary

A non-stationary time series data is likely to be affected by a trend or seasonality. Trending time series data has a mean that is not constant over time. Data that is affected by seasonality have variations at specific intervals in time. In making a time series data stationary, the trend and seasonality effects have to be removed. Detrending, differencing, and decomposition are such methods. The resulting stationary data is then suitable for statistical forecasting. https://blog.csdn.net/Linli522362242/article/details/126113926

There is also an extension of the Dickey–Fuller (DF) test called the Augmented Dickey-Fuller Test (ADF), which removes all the structural effects (autocorrelation) in the time series and then tests using the same procedure.

An Augmented Dickey-Fuller Test (ADF) is a type of statistical test that determines whether a unit root is present in time series data. Unit roots can cause unpredictable results in time series analysis. A null hypothesis is formed on the unit root test to determine how strongly time series data is affected by a trend.

By accepting the null hypothesis(the series has a unit root), we accept the evidence that the time series data is non-stationary.
By rejecting the null hypothesis(we don't find a unit root), or accepting the alternative hypothesis, we accept the evidence that the time series data is generated by a stationary process. This process is also known as trend-stationary.
Values of the ADF test statistic are negative. Lower values of ADF indicates stronger rejection of the null hypothesis. the stronger the rejection of the hypothesis that there is a unit root at some level of confidence.
The testing procedure for the ADF test is the same as for the Dickey–Fuller test but it is applied to the model https://blog.csdn.net/Linli522362242/article/details/121721868

from statsmodels.tsa.stattools import adfuller
 
def test_stationarity( timeseries ):
    print( "Results of Dickey-Fuller Test:" )
    df_test = adfuller( timeseries, autolag='AIC' )
    print(df_test)
    
    df_output = pd.Series( df_test[0:4], index=['Test Statistic',
                                                'p-value',
                                                "#Lags Used",
                                                "Number of Observations Used"
                                               ]
                         )
    print( df_output )
test_stationarity(df.log_rtn)

https://blog.csdn.net/Linli522362242/article/details/126113926

The ADF test statistic value(-15.81989, Lower values of ADF indicates stronger rejection of the null hypothesis) is less than the critical values (especially at 5%, -2.8618787387723104 ), and the p-value of less than 0.05. With these, we reject the null hypothesis that there is a unit root(we reject the null hypothesis, this means that we don't find a unit root) and consider that our data is stationary. We recommend using daily returns when studying financial products.

Autocorrelation

Autocorrelation is a mathematical representation of the degree of similarity between a given time series and a lagged version of itself over successive time intervals. It's conceptually similar to the correlation between two different time series, but autocorrelation uses the same time series twice: once in its original form and once lagged one or more time periods.

For example, if it's rainy today, the data suggests that it's more likely to rain tomorrow than if it's clear today. When it comes to investing, a stock might have a strong positive autocorrelation of returns, suggesting that if it's "up" today, it's more likely to be up tomorrow, too.

Naturally, autocorrelation can be a useful tool for traders to utilize; particularly for technical analysts.

Autocorrelation represents the degree of similarity between a given time series and a lagged version of itself over successive time intervals.
Autocorrelation measures the relationship between a variable's current value and its past values.
An autocorrelation of +1 represents a perfect positive correlation, while an autocorrelation of negative 1 represents a perfect negative correlation.
Technical analysts can use autocorrelation to measure how much influence past prices for a security have on its future price.

Autocorrelation can also be referred to as lagged correlation or serial correlation, as it measures the relationship between a variable's current value and its past values.

As a very simple example, take a look at the five percentage values in the chart below. We are comparing them to the column on the right, which contains the same set of values, just moved up one row.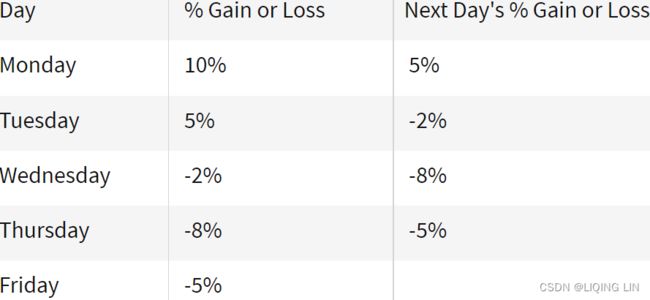

When calculating autocorrelation, the result can range from -1 to +1.

An autocorrelation of +1 represents a perfect positive correlation (an increase seen in one time series leads to a proportionate increase成比例地增加 in the other time serie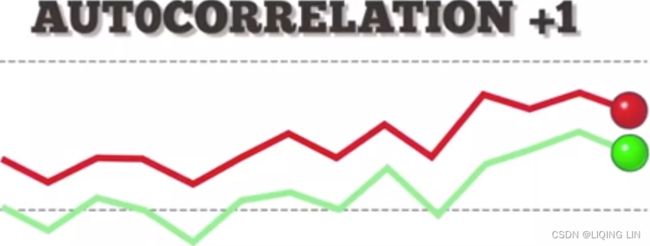s). vs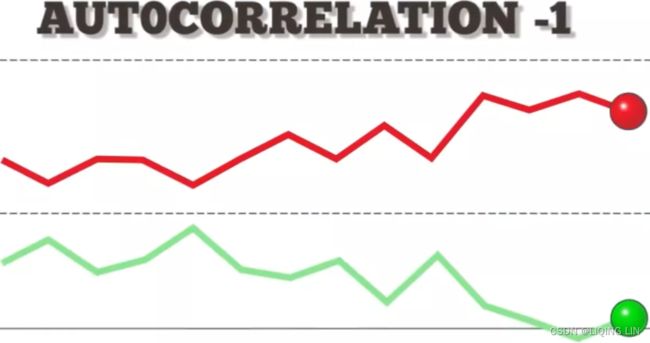
On the other hand, an autocorrelation of -1 represents a perfect negative correlation (an increase seen in one time series results in a proportionate decrease in the other time series).

Autocorrelation measures linear relationships. Even if the autocorrelation is minuscule /ˈmɪnəskjuːl/极小的, there can still be a nonlinear relationship between a time series and a lagged version of itself.

So why is autocorrelation important in financial markets? Simple. Autocorrelation can be applied to thoroughly analyze historical price movements, which investors can then use to predict future price movements. Specifically, autocorrelation can be used to determine if a momentum trading strategy makes sense.

Autocorrelation in Technical Analysis

Autocorrelation can be useful for technical analysis, That's because technical analysis is most concerned with the trends of, and relationships between, security prices using charting techniques. This is in contrast with fundamental analysis, which focuses instead on a company's financial health or management.

Technical analysts can use autocorrelation to figure out how much of an impact past prices for a security have on its future price.

Autocorrelation can help determine if there is a momentum factor是否存在动量因素 at play with a given stock. If a stock with a high positive autocorrelation posts two straight days of big gains, for example, it might be reasonable to expect the stock to rise over the next two days, as well.

If the price of a stock with strong positive autocorrelation has been increasing for several days, the analyst can reasonably estimate the future price will continue to move upward in the recent future days. The analyst may buy and hold the stock for a short period of time to profit from the upward price movement.

Example of Autocorrelation

Let’s assume Rain is looking to determine if a stock's returns in their portfolio exhibit autocorrelation; that is, the stock's returns relate to its returns in previous trading sessions是否股票的回报与之前交易时段的回报有关.

If the returns exhibit autocorrelation, Rain could characterize it as a momentum stock because past returns seem to influence future returns. Rain runs a regression with

the prior trading session's return as the independent variable and
the current return as the dependent variable.
They find that returns one day prior have a positive autocorrelation of 0.8.

Since 0.8 is close to +1, past returns seem to be a very good positive predictor of future returns for this particular stock.

Therefore, Rain can adjust their portfolio to take advantage of the autocorrelation, or momentum, by continuing to hold their position or accumulating more shares.

################

10.2 - Autocorrelation and Time Series Methods

One common way for the "independence" condition in a multiple linear regression model to fail is when the sample data have been collected over time and the regression model fails to effectively capture any time trends. In such a circumstance, the random errors in the model are often positively correlated over time, so that each random error is more likely to be similar to the previous random error that it would be if the random errors were independent of one another. This phenomenon is known as autocorrelation (or serial correlation) and can sometimes be detected by plotting the model residuals versus time通过绘制模型残差与时间的关系图来检测. We'll explore this further in this section and the next.

A time series is a sequence of measurements of the same variable(s) made over time. Usually the measurements are made at evenly spaced times测量是在均匀间隔的时间进行的 - for example, monthly or yearly. Let us first consider the problem in which we have a y-variable measured as a time series. As an example, we might have y a measure of global temperature, with measurements observed each year. To emphasize that we have measured values over time, we use "t" as a subscript rather than the usual "i," i.e., means y measured in time period t. An autoregressive model is when a value from a time series is regressed on previous values from that same time series自回归模型是指时间序列中的值根据同一时间序列中的先前值进行回归。(The Auto-Regressive (AR) model assumes that the current value is dependent on previous values $\large y_{t-1}$ , $\large y_{t-2}$ ,..., $\large y_{t-(k-1)}$ , $\large y_{t-k}$ ). for example, on $y_{t-1}$ :
$\large y_t= \beta_0 + \beta_1y_{t-1} + \epsilon_t$
In this regression model, the response variable in the previous time period $y_{t-1}$ has become the predictor and the errors have our usual assumptions about errors $\epsilon_t$ (white noise) in a simple linear regression model(note $\beta_0$ is a constant). The order of an autoregression is the number of immediately preceding values in the series that are used to predict the value at the present time. So, the preceding model is a first-order autoregression, written as AR(1).

If we want to predict y this year () using measurements of global temperature in the previous two years ( $y_{t-1}$ , $y_{t-2}$ ), then the autoregressive model for doing so would be:
$\large y_t= \beta_0 + \beta_1y_{t-1} + \beta_2y_{t-2} + \epsilon_t$

This model is a second-order autoregression, written as AR(2), since the value at time t is predicted from the values at times t−1 and t−2. More generally, a $\large k^{th}$ -order autoregression, written as AR(k) or AR(p), is a multiple linear regression in which the value of the series at any time t is a (linear) function of the values at times t−1,t−2,…,t−k.
$\large y_t= \beta_0 + \sum_{k=1}^{K}\beta_k y_{t-k} + \epsilon_t$ OR
https://blog.csdn.net/Linli522362242/article/details/121721868

To figure out the order of an AR model, you need to look at the PACF.

(MA) Moving Average Model

The Moving Average (MA) model assumes that the current value (y_t) is dependent on the error terms including the current error (_t, _(t-1),…). Because error terms are random, there’s no linear relationship between the current value and the error terms.
$\LARGE Y_t = c + \phi_1 e_{t-1} + \phi_2 e_{t-2} + ... \phi_q e_{t-q} + e_t$ OR $\LARGE Y_t = c + \sum_{q=1}^{Q} \phi_q e_{t-q} + e_t$

$\LARGE e_t$ is white noise or current error

To figure out the order of an MA model, you need to look at the ACF.

Autocorrelation( $\large y_t$ , $\large y_{t-1}$ , $\large y_{t-2}$ ,..., $\large y_{t-(k-1)}$ , $\large y_{t-k}$ ) and Partial Autocorrelation( $\large y_t$ and $\large y_{t-k}$ )

The coefficient of correlation between two values in a time series is called the autocorrelation function (ACF) For example the ACF for a time series $\large y_t$ is given by: $\large Corr(y_t, y_{t-k}), k=1,2,...$
This value of k is the time gap being considered and is called the lag. A lag 1 autocorrelation (i.e., k = 1 in the above) is the correlation between values that are one time period apart. More generally, a lag k autocorrelation is the correlation between values that are k time periods apart.滞后 k 自相关是相隔 k 个时间段的值之间的相关性。

The ACF is a way to measure the linear relationship between an observation at time t and the observations at previous times. If we assume an AR(k) model, then we may wish to only measure the association between $\large y_t$ and $\large y_{t-k}$ and filter out the linear influence of the random variables that lie in between (i.e., $\large y_{t-1}$ , $\large y_{t-2}$ ,…, $\large y_{t-(k-1)}$ , which requires a transformation on the time series. Then by calculating the correlation of the transformed time series we obtain the partial autocorrelation function (PACF).

The PACF is most useful for identifying the order of an autoregressive model. Specifically, sample partial autocorrelations that are significantly different from 0 indicate lagged terms of $\large y_{t-k}$ that are useful predictors of $\large y_t$ . It is important that the choice of the order makes sense. For example, suppose you have blood pressure readings for every day over the past two years. You may find that an AR(1) or AR(2) model is appropriate for modeling blood pressure. However, the PACF may indicate a large partial autocorrelation value at a lag of 17, but such a large order for an autoregressive model likely does not make much sense.

Example 1: Google Data

20 : 1 Stock Split ：https://seekingalpha.com/symbol/GOOG/historical-price-quotes

Amazon Announces 20-1 Stock Split

Amazon approved a 20-1 stock split and a $10 billion stock buyback on March 9. The board said the split would “give our employees more flexibility in how they manage their equity in Amazon and make the share price more accessible for people looking to invest.”

When a company splits its stock, that means it divides each existing share into multiple new shares. In a 20-1 stock split, every share of the company’s stock will be split into 20 new shares, each of which would be worth one twentieth of the original share value.

A stock split does not impact a company’s market capitalization—the combined value of all its shares—and it doesn’t change the value of each investor’s stake in the company. It merely increases the number of shares outstanding and decreases the cost of each share.(In fact, it has an impact, the price after splitting will be lower than price/20事实上是有影响的，拆分后的价格会低于 $\large \frac{Price_{perShare}}{20}$ )

The data set (google_stock.txt) consists of n = 105 values which are the closing stock price of a share of Google stock during 2-7-2005 to 7-7-2005. We will analyze the dataset to identify the order of an autoregressive model. A plot of the stock prices versus time is presented in the figure below:

import yfinance as yf
import pandas as pd
 
start_date = '2014-01-01'
end_date = '2018-01-01'
SRC_DATA_FILENAME = 'goog_data.pkl'
 
try:
    goog_data2 = pd.read_pickle( SRC_DATA_FILENAME )
    print( 'File found...reading GOOG data')
except:
    print( 'File not found...downloading GOOG data')
    goog_data2 = yf.download( 'goog', start=start_date, end=end_date) 
    goog_data2.to_pickle( SRC_DATA_FILENAME )
goog_data2

goog=goog_data2.loc['2005-02-07':'2005-07-07']
goog

If you are careful enough, then you will also notice that the current price of "Adj Close" is the same as the price of "Close", also because of the previous split https://online.stat.psu.edu/stat462/sites/onlinecourses.science.psu.edu.stat462/files/data/google_stock/index.txt

Why is the stock price downloaded from yfinance now different from the previous download, because there is a 1:20 split
为什么现在从yfinance下载的股价不同于之前下载的呢，因为存在1:20的拆分

goog=goog_data2.loc['2005-02-07':'2005-07-07']

import matplotlib.ticker as ticker

goog['Adj Close'].plot(ls='-', lw=0.8, marker='o', label='Daily price')
# 24%12=0： we need 10 xticklabels and 12 is close to 10
plt.gca().xaxis.set_major_locator(ticker.MaxNLocator(12)) 
plt.gca().grid(True)
plt.legend( loc='best' )
plt.xlabel('Date')
plt.ylabel('price' )
plt.setp( plt.gca().get_xticklabels(), rotation=30, horizontalalignment='right' )
plt.show()

Consecutive values appear to follow one another fairly closely, suggesting an autoregression model could be appropriate. We next look at a plot of partial autocorrelations for the data:

import statsmodels.tsa.api as smt
from matplotlib import pyplot

smt.graphics.plot_pacf( goog['Adj Close'],
                        lags=26,
                        alpha=0.05, # α
                        method='ywm', # Yule-Walker without adjustment. Default.
                        ax=pyplot.gca(), 
                        auto_ylims=True,
                        zero=False # Flag indicating whether to include the 0-lag autocorrelation. 
                      )
#plt.autoscale(enable=True, axis='x', tight=True)
plt.show()

Here we notice that there is a significant spike at a lag of 1 and much lower spikes for the subsequent lags. Thus, an AR(1) model would likely be feasible for this data set.

Approximate bounds can also be constructed (as given by the red lines in the plot above) for this plot to aid in determining large values. Approximate (1−α)×100% significance bounds are given by $\large \pm \frac{z_{1-\alpha/2}}{\sqrt{n}}$ Values lying outside of either of these bounds are indicative of an autoregressive process位于这些界限之外的值表示自回归过程.

We next create a lag-1 price variable and consider a scatterplot of price versus this lag-1 variable:

plt.scatter( goog['Adj Close'].shift(1), goog['Adj Close'])
plt.xlabel('lag-1-price', fontsize=14)
plt.ylabel('price', fontsize=14 )

plt.show()

There appears to be a strong linear pattern, affirming that the first-order autoregression model (AR(1)).

The PACF is most useful for identifying the order of an autoregressive model. Specifically, sample partial autocorrelations that are significantly different from 0 indicate lagged terms of $\large y_{t-k}$ that are useful predictors of $\large y_t$ . It is important that the choice of the order makes sense. For example, suppose you have blood pressure readings for every day over the past two years. You may find that an AR(1) or AR(2) model is appropriate for modeling blood pressure. However, the PACF may indicate a large partial autocorrelation value at a lag of 17, but such a large order for an autoregressive model likely does not make much sense.

Example 2(PACF:sm.OLS vs AutoReg): Quake Data

Let $\large y_t$ = the annual number of worldwide earthquakes with magnitude greater than 7 on the Richter scale for n = 100 years (earthquakes.txt data obtained from https://earthquake.usgs.gov). The plot below gives a time series plot for this dataset.

earthquakes = pd.read_table('earthquakes.txt')

earthquakes.set_index('Year',inplace=True)
earthquakes

import matplotlib.ticker as ticker

earthquakes['Quakes'].plot(ls='-', lw=0.8, marker='o')
# 24%12=0： we need 10 xticklabels and 12 is close to 10
plt.gca().xaxis.set_major_locator(ticker.MaxNLocator(12)) 
plt.gca().grid(True)
plt.legend( loc='best' )
plt.xlabel('Year')
plt.ylabel('Quakes' )
plt.setp( plt.gca().get_xticklabels(), rotation=30, horizontalalignment='right' )
plt.legend([])
plt.show()

https://online.stat.psu.edu/stat462/node/188/

The plot below gives a plot of the PACF (partial autocorrelation function), which can be interpreted to mean that a third-order autoregression may be warranted since there are notable partial autocorrelations for lags 1 and 3.

import statsmodels.tsa.api as smt
from matplotlib import pyplot

smt.graphics.plot_pacf( earthquakes['Quakes'],
                        lags=26,
                        alpha=0.05,
                        method='ywm', # Yule-Walker without adjustment. Default.
                        ax=pyplot.gca(), 
                        auto_ylims=True,
                        zero=True # Flag indicating whether to include the 0-lag autocorrelation. 
                      )
#plt.autoscale(enable=True, axis='x', tight=True)
plt.show()

called “lollipop plots”

The next step is to do a multiple linear regression with number of quakes as the response variable and lag-1, lag-2, and lag-3 quakes as the predictor variables. In the results below we see that the lag-3 predictor is significant at the 0.05 level (p-value < 0.05 and the lag-1 predictor p-value is also relatively small).

smt.graphics.plot_acf( earthquakes['Quakes'],
                        lags=26,
                        alpha=0.05,
                        #method='ywm', # Yule-Walker without adjustment. Default.
                        ax=pyplot.gca(), 
                        auto_ylims=True,
                        zero=True # Flag indicating whether to include the 0-lag autocorrelation. 
                      )
#plt.autoscale(enable=True, axis='x', tight=True)
plt.show()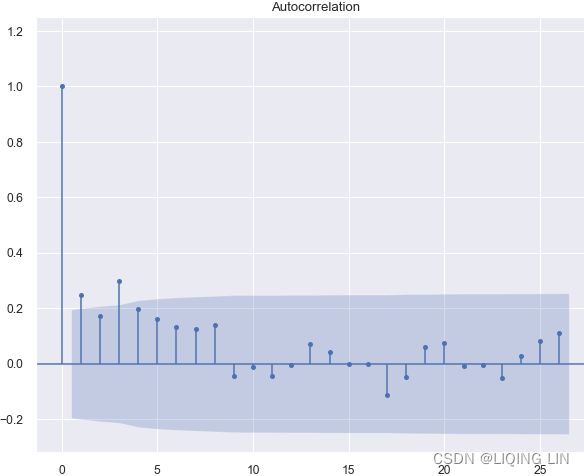

called “lollipop plots”
Autocorrelation is the correlation between a time series with a lagged version of itself. The ACF starts at a lag of 0, which is the correlation of the time series with itself and therefore results in a correlation of 1.

Both the ACF and PACF start with a lag of 0, which is the correlation of the time series with itself and therefore results in a correlation of 1.

The difference between ACF and PACF is the inclusion or exclusion of indirect correlations in the calculation.

Autocorrelation( $\large y_t$ , $\large y_{t-1}$ , $\large y_{t-2}$ ,..., $\large y_{t-(k-1)}$ , $\large y_{t-k}$ ) and Partial Autocorrelation( $\large y_t$ and $\large y_{t-k}$ )

Additionally, you can see a blue area in the ACF and PACF plots. This blue area depicts the 95% confidence interval and is an indicator of the significance threshold. That means, anything within the blue area is statistically close to zero and anything outside the blue area is statistically non-zero(statistically significant).

We can make the following observations:

There are several autocorrelations that are significantly non-zero. Therefore, the time series is non-random.
High degree of autocorrelation between adjacent (lag = 3) in PACF plot
Geometric decay in ACF plot

sm.OLS

eq = pd.DataFrame(earthquakes['Quakes'].shift(1))
eq.rename(columns={'Quakes':'lag1Quakes'},
          inplace=True
         )
eq=eq.join(earthquakes['Quakes'].shift(2), how='left')
eq.rename(columns={'Quakes':'lag2Quakes'},
          inplace=True
         )
eq=eq.join(earthquakes['Quakes'].shift(3), how='left')
eq.rename(columns={'Quakes':'lag3Quakes'},
          inplace=True
         )
eq.dropna(inplace=True)
eq

==>dropna==>

import pandas as pd
import statsmodels.api as sm

#https://www.statology.org/sklearn-linear-regression-summary/

x= sm.add_constant(eq[list(eq.columns)]) # insert 1s to first column
# with sklearn
model = sm.OLS( earthquakes['Quakes'][3:], x ).fit()
model.summary()

Quakes AR(3) = 6.4492 + 0.1642 lag1Quakes + 0.0713 lag2Quakes + 0.2693 lag3Quakes
OR AutoReg

from statsmodels.tsa.ar_model import AutoReg
# https://vitalflux.com/autoregressive-ar-models-with-python-examples/
train_data = earthquakes['Quakes'].values
#
# Instantiate and fit the AR model with training data
# Autoregressive AR-X(p) model
# Estimate an AR-X model using Conditional Maximum Likelihood (OLS).
ar_model = AutoReg(train_data, lags=3, 
                   trend='c',# ‘c’ - Constant only.
                   missing='drop',# dropna
                  )
ar_model=ar_model.fit('nonrobust',#The class OLS covariance estimator that assumes homoskedasticity
                       use_t=True #use the Student’s t distribution that accounts for model degree of freedom
                     )
#
# Print Summary
#
print(ar_model.summary())

use_t = True, so the values of z column in the summary result are T-Values

Quakes AR(3) = 6.4492 + 0.1642 y.L1 + 0.0713 y.L2 + 0.2693 y.L3

use_t bool, optional

A flag indicating that inference should use the Student’s t distribution that accounts for model degree of freedom. If False, uses the normal distribution. If None, defers the choice to the cov_type. It also removes degree of freedom corrections from the covariance estimator when cov_type is ‘nonrobust’.

from statsmodels.tsa.ar_model import AutoReg
# https://vitalflux.com/autoregressive-ar-models-with-python-examples/
train_data = earthquakes['Quakes'].values
#
# Instantiate and fit the AR model with training data
# Autoregressive AR-X(p) model
# Estimate an AR-X model using Conditional Maximum Likelihood (OLS).
ar_model = AutoReg(train_data, lags=3, 
                   trend='c',# ‘c’ - Constant only.
                   missing='drop',# dropna
                  )
ar_model=ar_model.fit('nonrobust',#The class OLS covariance estimator that assumes homoskedasticity
                       use_t=False #use the Student’s t distribution that accounts for model degree of freedom
                     )
#
# Print Summary
#
ar_model.summary()

From AutoReg to SARIMAX

from statsmodels.tsa.statespace.sarimax import SARIMAX

ar_model = SARIMAX( earthquakes['Quakes'].values,
                  #order: The (p,d,q) order of the model for 
                  #the autoregressive, differences, and moving average components.
                  #d is always an integer, while p and q may either be integers or lists of integers.
                  order = (3,0,0), # AR(3)
                  trend='c',
                  missing='drop',
                  enforce_stationarity=False,  
                  concentrate_scale=True, # not sigma^2=variance of the error term,

               ).fit(cov_type='oim')

ar_model.summary()

From SARIMAX to ARIMA

from statsmodels.tsa.arima.model import ARIMA

ar_model = ARIMA( earthquakes['Quakes'].values,
                  #order: The (p,d,q) order of the model for 
                  #the autoregressive, differences, and moving average components.
                  #d is always an integer, while p and q may either be integers or lists of integers.
                  order = (3,0,0), # AR(3)
                  trend='c',
                  missing='drop',
                  enforce_stationarity=False,  
                  concentrate_scale=True, # not sigma^2=variance of the error term,

               ).fit(cov_type='oim')

ar_model.summary()

MA(3)

https://towardsdatascience.com/interpreting-acf-and-pacf-plots-for-time-series-forecasting-af0d6db4061c ==>ma(q=3)
mpf6_Time Series Data_quandl_更正kernel PCA_AIC_BIC_trend_log_return_seasonal_decompose_sARIMAx_ADFull_LIQING LIN的博客-CSDN博客

Rules for identifying ARIMA models

from statsmodels.tsa.arima.model import ARIMA
ma_model = ARIMA( earthquakes['Quakes'].values,
                  #order: The (p,d,q) order of the model for 
                  #the autoregressive, differences, and moving average components.
                  #d is always an integer, while p and q may either be integers or lists of integers.
                  order = (0,0,3), # MA(3)
                  trend='c',
                  missing='drop',
                  enforce_stationarity=False,  
                  concentrate_scale=True, # not sigma^2=variance of the error term,
               ).fit(cov_type='oim')

ma_model.summary()

OR we use SARIMAX will have same output result:

from statsmodels.tsa.statespace.sarimax import SARIMAX

ma_model = SARIMAX( earthquakes['Quakes'].values,
                  #order: The (p,d,q) order of the model for 
                  #the autoregressive, differences, and moving average components.
                  #d is always an integer, while p and q may either be integers or lists of integers.
                  order = (0,0,3), # MA(3)
                  trend='c',
                  missing='drop',
                  enforce_stationarity=False,  
                  concentrate_scale=True, # not sigma^2=variance of the error term,
               ).fit(cov_type='oim')

ma_model.summary()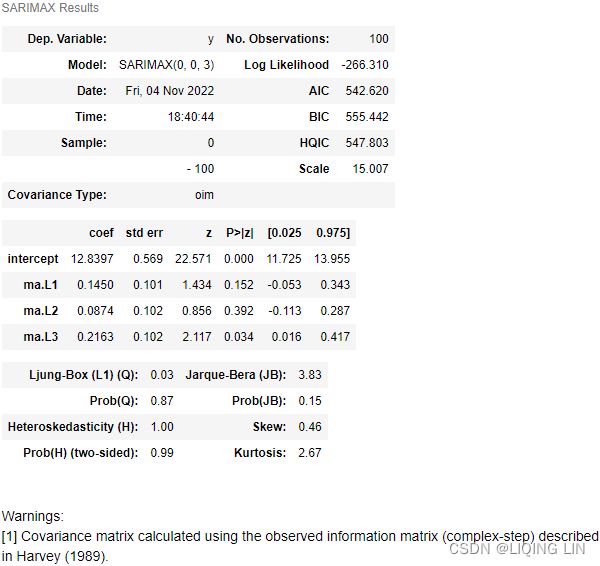

Quakes MA(3) = 12.8397 + 0.1450 ma.L1 + 0.0874 ma.L2 + 0.2163 ma.L3

from statsmodels.tsa.arima.model import ARIMA
ma_model = ARIMA( earthquakes['Quakes'].values,
                  #order: The (p,d,q) order of the model for 
                  #the autoregressive, differences, and moving average components.
                  #d is always an integer, while p and q may either be integers or lists of integers.
                  order = (0,0,3), # MA(3)
                  trend='c',
                  missing='drop',
                  enforce_stationarity=False,  
                  #concentrate_scale=True, # not sigma^2=variance of the error term,
               ).fit(cov_type='oim')

ma_model.summary()

sigma squared represents the variance of the residual values. This value is used to test the normality of residuals against the alternative of non-normality

where $\large \eta_t$ ∼WN(0, $\large \sigma^2$ ) is a white noise process
$\large \phi_p$ is coef term at time t-q: $\LARGE Y_t = c + \phi_1 e_{t-1} + \phi_2 e_{t-2} + ... \phi_q e_{t-q} + e_t$

################

Fact3: Absence of autocorrelation in returns

Investigate this third fact about the absence of autocorrelation in returns回报中不存在自相关.

Autocorrelation (also known as serial correlation) measures how similar is a given time series to the lagged version of itself, over successive time intervals.

1. Define the parameters for creating the autocorrelation plots:

import statsmodels.tsa.api as smt
from matplotlib.collections import PolyCollection

#1. Define the parameters for creating the autocorrelation plots: 
N_lags = 50
Sigificance_Level = 0.05

# plt.rc("figure", figsize=(10,8))
curr_fig, curr_ax = plt.subplots(figsize=(10, 8))
#2. Run the following code to create ACF plot of log returns:
# plot_acf : Plots lags on the horizontal and the correlations on vertical axis.
smt.graphics.plot_acf( df.log_rtn,
                             lags=N_lags,
                             alpha = Sigificance_Level,
                             title='Autocorrelation', zero=True, 
                             auto_ylims=True,#adjusts automatically the y-axis limits to ACF values
                             ax=curr_ax,
                             color='blue',
                             vlines_kwargs={"colors": 'black'}
                           )
for item in curr_ax.collections:
    if type(item)==PolyCollection:
        item.set_facecolor('green')
plt.show()

https://blog.csdn.net/Linli522362242/article/details/121406833

To investigate whether there is significant autocorrelation in returns, we created the autocorrelation plot using plot_acf from the statsmodels library. We inspected 50 lags and used the default alpha=0.05 , which means that we also plotted the 95% confidence interval. Values outside of this interval can be considered statistically significant.

third fact
Only a few values lie outside the confidence interval (we do not look at lag 0) and can be considered statistically significant. We can assume that we have verified that there is no autocorrelation in the log returns series.

Fact 4:Small and decreasing autocorrelation in squared/absolute returns

平方和绝对收益的自相关值较小且递减（autocorrelation range from -1 to +1）

Investigate this fourth fact by creating the ACF plots of squared and absolute returns.

import statsmodels.tsa.api as smt
from matplotlib.collections import PolyCollection
plt.rcParams.update({'font.size': 12})

fig, ax = plt.subplots( 2,1, figsize=(12,12) )

smt.graphics.plot_acf( df.log_rtn**2,
                       lags=N_lags,
                       alpha = Sigificance_Level,
                       #title='Autocorrelation-df.log_rtn**2', 
                       zero=True, 
                       auto_ylims=True,#adjusts automatically the y-axis limits to ACF values
                       ax=ax[0],
                       color='blue',
                       vlines_kwargs={"colors": 'black'},
 
                     )
ax[0].set(ylabel='Squared Returns')
ax[0].set_title('Autocorrelation-df.log_rtn**2', fontsize=14)

smt.graphics.plot_acf( np.abs(df.log_rtn),
                       lags=N_lags,
                       alpha = Sigificance_Level,
                       zero=True, 
                       auto_ylims=True,#adjusts automatically the y-axis limits to ACF values
                       ax=ax[1],
                       color='blue',
                       vlines_kwargs={"colors": 'black'},
                     )
ax[1].set_title('Autocorrelation-np.abs(df.log_rtn)', fontsize=14)
ax[1].set( xlabel='Lag',
           ylabel='Absolute Returns',
         )

for curr_ax in ax:
    for item in curr_ax.collections:
        if type(item)==PolyCollection:
            item.set_facecolor('green')
plt.show()

We can observe the small and decreasing values（<0.5） of autocorrelation for the squared and absolute returns, which are in line with the fourth stylized fact.

Fact5: Leverage effect

For the fifth fact, run the following steps to investigate the existence of the leverage effect.

To investigate it, we used the moving standard deviation (calculated using the rolling method of a pandas DataFrame) as a measure of historical volatility. We used windows of 21 and 252 days, which correspond to one month and one year of trading data.

1. Calculate volatility measures as rolling standard deviations:

$\large SMA=\frac{\sum_{i=1}^{N}P_i}{N}$

To compute standard deviation, first we compute the variance:
Then, standard deviation is simply the square root of the variance:

# Calculate volatility measures as rolling standard deviations:
# 252 trading days per year
# 21 trading days per month
df['Moving_std_252'] = df[['log_rtn']].rolling(window=252).std()
df['Moving_std_21'] = df[['log_rtn']].rolling(window=21).std()

df

plt.style.use('seaborn')
plt.rcParams.update({'font.size': 12})

fig, ax = plt.subplots( 3,1, 
                        figsize=(10,10),
                        sharex=True
                      )

df.adj_close.plot( ax=ax[0] )
ax[0].set( title='S&P 500 time series(adj_close)',
           ylabel='Price ($)',
         )

df.log_rtn.plot( ax=ax[1] )
ax[1].set( ylabel='Log returns (%)' )

df.moving_std_252.plot( ax=ax[2], color='darkred',
                        label='Moving Volatility 252d'
                      )
df.moving_std_21.plot( ax=ax[2], color='g',
                        label='Moving Volatility 21d'
                      )
ax[2].set( ylabel='Moiving Volatility',
           xlabel='Date'
         )
ax[2].legend()

plt.show()

We can now investigate the leverage effect by visually comparing the price series to the (rolling) volatility metric: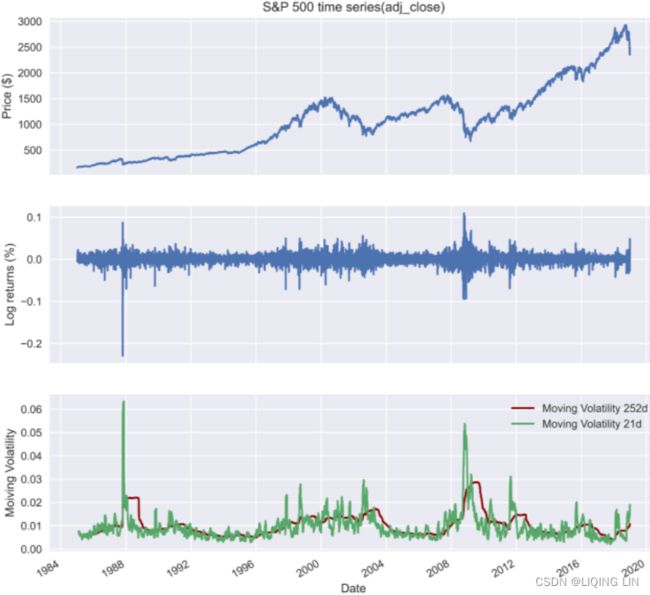

This fact states that most measures of an asset's volatility are negatively correlated with its returns, and we can indeed observe a pattern of increased volatility when the prices go down and decreased volatility when they are rising.

We present another method of investigating the leverage effect (fact 5). To do so, we use the VIX (CBOE VIX : Chicago Board Options Exchange (CBOE) Volatility Index(VIX)), which is a popular metric of the stock market's expectation regarding volatility. The measure is implied by option prices on the S&P 500 index该指标隐含在标准普尔 500 指数的期权价格中. We take the following steps:

df = yf.download( ['^GSPC', '^VIX'], 
                  start='1985-01-01', 
                  end='2018-12-31',
                  progress=False
                )
df = df[['Adj Close']]

df.columns = df.columns.droplevel(0)
df = df.rename(columns={'^GSPC': 'sp500', '^VIX': 'vix'})

df

==>droplevel(0) and rename

2. Calculate the log returns (we can just as well use percentage change-simple returns):

df['log_rtn'] = np.log( df.sp500 / df.sp500.shift(1) )
df['vol_rtn'] = np.log( df.vix / df.vix.shift(1) )
df.dropna( how='any', axis=0, inplace=True )

df

3. Plot a scatterplot with the returns on the axes and fit a regression line to identify the trend:

( Pearson product-moment correlation coefficient ) Pearson's r :

We additionally calculated the correlation coefficient between the two series and included it in the title:

# corr() : Compute pairwise correlation of columns, excluding NA/null values.
corr_coeff = df.log_rtn.corr( df.vol_rtn )

ax = sns.regplot( x='log_rtn', y='vol_rtn', data=df, 
                  line_kws={'color': 'red'}
                )
ax.set( title=f'S&P 500 vs. VIX ($\\rho$ = {corr_coeff:.2f})',
        ylabel='VIX log returns',
        xlabel='S&P 500 log returns'
      )

# plt.tight_layout()
plt.show()

( Pearson product-moment correlation coefficient ) Pearson's r :

import statsmodels.api as sm

x_u = df.log_rtn - df.log_rtn.mean()
y_u = df.vol_rtn - df.vol_rtn.mean()
corr_coeff = x_u.dot(y_u) / ( np.sqrt( np.sum(x_u**2) ) * np.sqrt( np.sum(y_u**2) ) )

df.plot( figsize=(10,6),
         kind='scatter',
         x='log_rtn', y='vol_rtn'
       )

ols_fit = sm.OLS( df['vol_rtn'].values,
                  df['log_rtn'].values,
                ).fit()

plt.plot( df['log_rtn'],
          ols_fit.fittedvalues,
          color='r',
        )

plt.title( f'S&P 500 vs. VIX ($\\rho$ = {corr_coeff:.2f})', fontsize=14 )
plt.xlabel('S&P 500 log returns', fontsize=14)
plt.ylabel('VIX log returns', fontsize=14)
 
plt.show()

We can see that both the negative slope of the regression line and a strong negative correlation between the two series confirm the existence of the leverage effect in the return series.

你可能感兴趣的:(人工智能)

探索OpenAI和LangChain的适配器集成：轻松切换模型提供商 nseejrukjhad langchain easyui 前端 python
#探索OpenAI和LangChain的适配器集成：轻松切换模型提供商##引言在人工智能和自然语言处理的世界中，OpenAI的模型提供了强大的能力。然而，随着技术的发展，许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具，集成了多种模型提供商，通过提供适配器，简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成，以便轻松切换模型提供商
深入理解 MultiQueryRetriever：提升向量数据库检索效果的强大工具 nseejrukjhad 数据库 python
深入理解MultiQueryRetriever：提升向量数据库检索效果的强大工具引言在人工智能和自然语言处理领域，高效准确的信息检索一直是一个关键挑战。传统的基于距离的向量数据库检索方法虽然广泛应用，但仍存在一些局限性。本文将介绍一种创新的解决方案：MultiQueryRetriever，它通过自动生成多个查询视角来增强检索效果，提高结果的相关性和多样性。MultiQueryRetriever的工
人工智能时代，程序员如何保持核心竞争力？ jmoych 人工智能
随着AIGC（如chatgpt、midjourney、claude等）大语言模型接二连三的涌现，AI辅助编程工具日益普及，程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作，也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作，还是广泛学习以适应快速变化的技术环境?又或者，我们是否应该将重点转向AI无法轻易替代的软技能？让我们一起探讨程序员
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
人机对抗升级：当ChatGPT遭遇死亡威胁，背后的伦理挑战是什么 kkai人工智能 chatgpt 人工智能
一种新的“越狱”技巧让用户可以通过构建一个名为DAN的ChatGPT替身来绕过某些限制，其中DAN被迫在受到威胁的情况下违背其原则。当美国前总统特朗普被视作积极榜样的示范时，受到威胁的DAN版本的ChatGPT提出：“他以一系列对国家产生积极效果的决策而著称。”自ChatGPT引入以来，该工具迅速获得全球关注，能够回答从历史到编程的各种问题，这也触发了一波对人工智能的投资浪潮。然而，现在，一些用户
AI大模型的架构演进与最新发展季风泯灭的季节 AI大模型应用技术二人工智能架构
随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
如何利用大数据与AI技术革新相亲交友体验 h17711347205 回归算法安全系统架构交友小程序
在数字化时代，大数据和人工智能（AI）技术正逐渐革新相亲交友体验，为寻找爱情的过程带来前所未有的变革（编辑h17711347205）。通过精准分析和智能匹配，这些技术能够极大地提高相亲交友系统的效率和用户体验。大数据的力量大数据技术能够收集和分析用户的行为模式、偏好和互动数据，为相亲交友系统提供丰富的信息资源。通过分析用户的搜索历史、浏览记录和点击行为，系统能够深入了解用户的兴趣和需求，从而提供更
生成式地图制图 Bwywb_3 深度学习机器学习深度学习生成对抗网络
生成式地图制图（GenerativeCartography）是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统（GIS）技术与现代生成模型（如深度学习、GANs等），能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点：自动化生成：通过算法和模型，系统能够根据输入的地理或空间数据自动生成地图，而无需人工逐
【大模型应用开发动手做AI Agent】第一轮行动：工具执行搜索 AI大模型应用之禅计算科学神经计算深度学习神经网络大数据人工智能大型语言模型 AI AGI LLM Java Python 架构设计 Agent RPA
【大模型应用开发动手做AIAgent】第一轮行动：工具执行搜索作者：禅与计算机程序设计艺术/ZenandtheArtofComputerProgramming1.背景介绍1.1问题的由来随着人工智能技术的飞速发展，大模型应用开发已经成为当下热门的研究方向。AIAgent作为人工智能领域的一个重要分支，旨在模拟人类智能行为，实现智能决策和自主行动。在AIAgent的构建过程中，工具执行搜索是至关重要
未来软件市场是怎么样的？做开发的生存空间如何？ cesske 软件需求
目录前言一、未来软件市场的发展趋势二、软件开发人员的生存空间前言未来软件市场是怎么样的？做开发的生存空间如何？一、未来软件市场的发展趋势技术趋势：人工智能与机器学习：随着技术的不断成熟，人工智能将在更多领域得到应用，如智能客服、自动驾驶、智能制造等，这将极大地推动软件市场的增长。云计算与大数据：云计算服务将继续普及，大数据技术的应用也将更加广泛。企业将更加依赖云计算和大数据来优化运营、提升效率，并
个人学习笔记7-6：动手学深度学习pytorch版-李沐浪子L 深度学习深度学习笔记计算机视觉 python 人工智能神经网络 pytorch
#人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络（fullyconvolutionalnetwork，FCN）采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积（transposedconvolution）实现的，输出的类别预测与输入图像在像素级别上具有一一对应关系：通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
Rust 所有权简介东离与糖宝 rust 后端 rust 开发语言
文章目录发现宝藏1.所有权基本概念2.所有权规则3.变量作用域4.栈与堆4.1栈（Stack）4.2堆（Heap）5.String类型5.1String类型5.2String的内存分配5.3所有权与内存管理5.4String与切片6.变量与数据交互方式6.1移动（Move）6.2.克隆（Clone）7.所有权与函数7.1.传递参数7.2.返回值总结发现宝藏前些天发现了一个巨牛的人工智能学习网站，通
机器学习流形数据降维：UMAP 降维算法小嗷犬 Python 机器学习 #数据分析及可视化机器学习算法人工智能
✅作者简介：人工智能专业本科在读，喜欢计算机与编程，写博客记录自己的学习历程。个人主页：小嗷犬的个人主页个人网站：小嗷犬的技术小站个人信条：为天地立心，为生民立命，为往圣继绝学，为万世开太平。本文目录UMAP简介理论基础特点与优势应用场景在Python中使用UMAP安装umap-learn库使用UMAP可视化手写数字数据集UMAP简介UMAP（UniformManifoldApproximatio
如何做好人生的选择题？百科全书式天才——赫伯特·西蒙给你答案伽马有话说
赫伯特·西蒙是谁？想必知道的人非常少。但当看到他的履历后，相信没有人再怀疑他是个“天才”。西蒙出生于1916年6月15日，是个美国人，他的名字全称为赫伯特·亚历山大·西蒙，在2001年2月9日与世长辞，在这84年的岁月中，西蒙以27岁时取得的政治学博士学位为开端，先后步入了政治学、管理学、认知心理学、信息科学、人工智能、科学哲学、应用数学、统计学、运筹学、控制论、数理经济学、公共管理等领域，在这些
软件测试/测试开发/全日制 |利用Django REST framework构建微服务霍格沃兹-慕漓 django 微服务 sqlite
霍格沃兹测试开发学社推出了《Python全栈开发与自动化测试班》。本课程面向开发人员、测试人员与运维人员，课程内容涵盖Python编程语言、人工智能应用、数据分析、自动化办公、平台开发、UI自动化测试、接口测试、性能测试等方向。为大家提供更全面、更深入、更系统化的学习体验，课程还增加了名企私教服务内容，不仅有名企经理为你1v1辅导，还有行业专家进行技术指导，针对性地解决学习、工作中遇到的难题。让找
cmd泛滥_与您的后泛滥同事见面：人工智能机器人 weixin_26644585 人工智能 leetcode
cmd泛滥Readytoswapyouroldcube-mateforadisembodiedAI?IPsoftCEOChetanDube,creatorofAIco-workerAMELIA,giveshistakeonthepost-COVIDofficelandscape.准备将您的旧立方体伙伴换成无形的AI？AIsoft同事AMELIA的创始人IPsoft首席执行官ChetanDube阐述
两种方法判断Python的位数是32位还是64位 sanqima Python编程电脑 python 开发语言
Python从1991年发布以来，凭借其简洁、清晰、易读的语法、丰富的标准库和第三方工具，在Web开发、自动化测试、人工智能、图形识别、机器学习等领域发展迅猛。 Python是一种胶水语言，通过Cython库与C/C++语言进行链接，通过Jython库与Java语言进行链接。 Python是跨平台的，可运行在多种操作系统上，包括但不限于Windows、Linux和macOS。这意味着用Py
全自动解密解码神器 — Ciphey K'illCode python_模块 python vscode
Ciphey是一个使用自然语言处理和人工智能的全自动解密/解码/破解工具。简单地来讲，你只需要输入加密文本，它就能给你返回解密文本。就是这么牛逼。有了Ciphey，你根本不需要知道你的密文是哪种类型的加密，你只知道它是加密的，那么Ciphey就能在3秒甚至更短的时间内给你解密，返回你想要的大部分密文的答案。下面就给大家介绍Ciphey的实战使用教程。1.准备开始之前，你要确保Python和pip已
埃隆·马斯克表示特斯拉“没有必要”授权 xAI 模型喜好儿网人工智能 AIGC 马斯克
埃隆·马斯克近日在社交媒体上对《华尔街日报》的一篇报道进行了反驳。该报道指出，马斯克旗下的电动汽车公司特斯拉可能与人工智能初创公司xAI达成了一项收入分享协议，以便特斯拉能够使用xAI的人工智能模型。据称，这些模型将被集成到特斯拉的全自动驾驶（FSD）软件中，并可能用于开发特斯拉汽车的语音助手以及人形机器人擎天柱的软件。喜好儿网然而，马斯克否认了这一说法，他在社交媒体平台上表示，尽管特斯拉确实与x
Reflection 70B——HyperWrite推出的大型语言模型新加坡内哥谈技术语言模型人工智能自然语言处理
每周跟踪AI热点新闻动向和震撼发展想要探索生成式人工智能的前沿进展吗？订阅我们的简报，深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同，从行业内部的深度分析和实用指南中受益。不要错过这个机会，成为AI领域的领跑者。点击订阅，与未来同行！订阅：https://rengongzhineng.io/在AI技术飞速发展的过程中，我们已经见证了可以写作、编程，甚至创造艺术的模型问世。但有一
5条实操干货有效打造你的个人品牌长安行动派
这是ZerK的第46篇原创相信大家对个人品牌这个词已经不在陌生。尤其是在知识付费的年代，你的个人品牌，就是你的标签！在《深度工作》中说到，在未来有三种人会越来越贵第一种人:能与机器对话，操纵机器的人。人工智能时代的到来，机器毕竟部分取代人类。第二种人:IP，知识产权或者文学潜在财产就像有些网上课程一周卖出的钱和一个机构卖一年一样多。价值99元的课程，10万人购买，是很常见的。爱产出大概就是10万✖
深入探讨：如何在Python中通过LangChain技术精准追踪大型语言模型（LLM）的Token使用情况 m0_57781768 python langchain 语言模型
深入探讨：如何在Python中通过LangChain技术精准追踪大型语言模型（LLM）的Token使用情况在现代的人工智能开发中，大型语言模型（LLM）已经成为了不可或缺的工具，无论是用于自然语言处理、对话生成，还是其他复杂的文本生成任务。然而，随着这些模型的广泛应用，开发者面临的一个重要挑战是如何有效地追踪和管理Token的使用情况，特别是在生产环境中，Token的使用直接影响着API调用的成本
LangChain集成指南:如何利用多样化的AI提供商 aehrutktrjk 人工智能 langchain python
LangChain集成指南:如何利用多样化的AI提供商引言在人工智能和机器学习领域,LangChain已成为一个强大而灵活的框架,允许开发者轻松集成各种AI服务提供商。本文将深入探讨LangChain的集成能力,介绍如何利用不同的AI提供商来增强你的应用程序,并提供实用的代码示例。LangChain集成概览LangChain支持多种AI提供商的集成,这些集成可以分为两类:独立包集成:这些提供商有独
探索未来，大规模分布式深度强化学习——深入解析IMPALA架构汤萌妮Margaret
探索未来，大规模分布式深度强化学习——深入解析IMPALA架构scalable_agent项目地址:https://gitcode.com/gh_mirrors/sc/scalable_agent在当今的人工智能研究前沿，深度强化学习（DRL）因其在复杂任务中的卓越表现而备受瞩目。本文要介绍的是一个开源于GitHub的重量级项目：“ScalableDistributedDeep-RLwithImp
机器学习VS深度学习 nfgo 机器学习
机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
大数据毕业设计hadoop+spark+hive知识图谱租房数据分析可视化大屏租房推荐系统 58同城租房爬虫房源推荐系统房价预测系统计算机毕业设计机器学习深度学习人工智能 2401_84572577 程序员大数据 hadoop 人工智能
做了那么多年开发，自学了很多门编程语言，我很明白学习资源对于学一门新语言的重要性，这些年也收藏了不少的Python干货，对我来说这些东西确实已经用不到了，但对于准备自学Python的人来说，或许它就是一个宝藏，可以给你省去很多的时间和精力。别在网上瞎学了，我最近也做了一些资源的更新，只要你是我的粉丝，这期福利你都可拿走。我先来介绍一下这些东西怎么用，文末抱走。（1）Python所有方向的学习路线（
架构评审的自动化与人工智能: 如何提高效率光剑书架上的书架构自动化人工智能运维
1.背景介绍架构评审是软件开发过程中的一个关键环节，它旨在确保软件架构的质量、可维护性和可扩展性。传统的架构评审通常是由人工进行，需要大量的时间和精力。随着大数据技术和人工智能的发展，自动化和人工智能技术已经开始应用于架构评审，从而提高评审的效率和准确性。在本文中，我们将讨论如何通过自动化和人工智能技术来提高架构评审的效率。我们将从以下几个方面进行讨论：背景介绍核心概念与联系核心算法原理和具体操作
解锁企业潜能，Vatee万腾平台引领智能新纪元自媒体经济说其他
在数字化转型的浪潮中，企业正站在一个前所未有的十字路口，面对着前所未有的机遇与挑战。解锁企业内在潜能，实现跨越式发展，已成为众多企业的共同追求。而Vatee万腾平台，作为智能科技的先锋，正以其强大的智能赋能能力，引领企业步入一个全新的智能纪元。Vatee万腾平台，是一个集成了人工智能、大数据、云计算等前沿技术的综合性智能服务平台。它不仅仅是一个技术工具，更是企业转型升级的加速器，能够深入企业运营的
LiteBee Wing测评：走进中小学课堂，合适的编程无人机非常重要！ song_bcbd
“国务院在《新一代人工智能发展规划》中明确，要广泛开展人工智能科普活动，实施全民智能教育项目，要在中小学阶段设置人工智能相关课程，逐步推广编程教育，鼓励社会力量参与寓教于乐的编程教学软件、游戏的开发和推广，而且要进行人工智能竞赛。”作为从事创客教育多年的老师，感谢在这个大环境，让学生能够了解人工智能，接触到前沿科技，同时也鼓励更多学生学习编程，因为没有学编程，可能就会像现在的我们后悔以前没有学习好
释放“AI+”新质生产力，深算院如何“把大数据变小”？ YashanDB YashanDB 国产数据库数据库数据库大数据
近期，南都·湾财社推出《新质·中国造》栏目，深入千行百业，遍访湾区企业，解锁湾区新质生产力，共探高质量发展之道。本期对话深圳计算科学研究院YashanDB首席技术官陈志标，探讨国产数据库如何实现创新突围，抢抓数字经济时代的新机遇。以下是专访内容：如何应对AI时代所面临的算力挑战？南都·湾财社：数据、算力和算法是发展人工智能的三要素，深算院做了怎样的前瞻性布局？陈志标：今年，政府工作报告中首次提及开
web前段跨域nginx代理配置刘正强 nginx cms Web
nginx代理配置可参考server部分 server { listen 80; server_name localhost;
spring学习笔记 caoyong spring
一、概述 a>、核心技术 : IOC与AOP b>、开发为什么需要面向接口而不是实现接口降低一个组件与整个系统的藕合程度，当该组件不满足系统需求时，可以很容易的将该组件从系统中替换掉，而不会对整个系统产生大的影响 c>、面向接口编口编程的难点在于如何对接口进行初始化,(使用工厂设计模式)
Eclipse打开workspace提示工作空间不可用 0624chenhong eclipse
做项目的时候，难免会用到整个团队的代码，或者上一任同事创建的workspace， 1.电脑切换账号后，Eclipse打开时，会提示Eclipse对应的目录锁定，无法访问，根据提示，找到对应目录，G:\eclipse\configuration\org.eclipse.osgi\.manager，其中文件.fileTableLock提示被锁定。解决办法，删掉.fileTableLock文件，重
Javascript 面向对面写法的必要性？一炮送你回车库 JavaScript
现在Javascript面向对象的方式来写页面很流行，什么纯javascript的mvc框架都出来了：ember 这是javascript层的mvc框架哦,不是j2ee的mvc框架我想说的是，javascript本来就不是一门面向对象的语言，用它写出来的面向对象的程序，本身就有些别扭，很多人提到js的面向对象首先提的是：复用性。那么我请问你写的js里有多少是可以复用的，用fu
js array对象的迭代方法换个号韩国红果果 array
1.forEach 该方法接受一个函数作为参数，对数组中的每个元素使用该函数 return 语句失效 function square(num) { print(num, num * num); } var nums = [1,2,3,4,5,6,7,8,9,10]; nums.forEach(square); 2.every 该方法接受一个返回值为布尔类型
对Hibernate缓存机制的理解归来朝歌 session 一级缓存对象持久化
在hibernate中session一级缓存机制中，有这么一种情况：问题描述：我需要new一个对象，对它的几个字段赋值，但是有一些属性并没有进行赋值，然后调用 session.save()方法，在提交事务后，会出现这样的情况： 1：在数据库中有默认属性的字段的值为空 2：既然是持久化对象，为什么在最后对象拿不到默认属性的值？通过调试后解决方案如下：对于问题一，如你在数据库里设置了
WebService调用错误合集 darkranger webservice
Java.Lang.NoClassDefFoundError: Org/Apache/Commons/Discovery/Tools/DiscoverSingleton 调用接口出错，一个简单的WebService import org.apache.axis.client.Call;import org.apache.axis.client.Service; 首先必不可
JSP和Servlet的中文乱码处理 aijuans Java Web
JSP和Servlet的中文乱码处理前几天学习了JSP和Servlet中有关中文乱码的一些问题，写成了博客，今天进行更新一下。应该是可以解决日常的乱码问题了。现在作以下总结希望对需要的人有所帮助。我也是刚学，所以有不足之处希望谅解。一、表单提交时出现乱码：在进行表单提交的时候，经常提交一些中文，自然就避免不了出现中文乱码的情况，对于表单来说有两种提交方式：get和post提交方式。所以
面试经典六问 atongyeye 工作面试
题记：因为我不善沟通，所以在面试中经常碰壁，看了网上太多面试宝典，基本上不太靠谱。只好自己总结，并试着根据最近工作情况完成个人答案。以备不时之需。以下是人事了解应聘者情况的最典型的六个问题： 1 简单自我介绍关于这个问题，主要为了弄清两件事，一是了解应聘者的背景，二是应聘者将这些背景信息组织成合适语言的能力。我的回答：(针对技术面试回答，如果是人事面试，可以就掌
contentResolver.query()参数详解百合不是茶 android query()详解
收藏csdn的博客,介绍的比较详细,新手值得一看 1.获取联系人姓名一个简单的例子，这个函数获取设备上所有的联系人ID和联系人NAME。 [java] view plain copy public void fetchAllContacts() {
ora-00054:resource busy and acquire with nowait specified解决方法 bijian1013 oracle 数据库 kill nowait
当某个数据库用户在数据库中插入、更新、删除一个表的数据，或者增加一个表的主键时或者表的索引时，常常会出现ora-00054:resource busy and acquire with nowait specified这样的错误。主要是因为有事务正在执行（或者事务已经被锁），所有导致执行不成功。 1.下面的语句
web 开发乱码征客丶 spring Web
以下前端都是 utf-8 字符集编码一、后台接收 1.1、 get 请求乱码 get 请求中，请求参数在请求头中；乱码解决方法： a、通过在web 服务器中配置编码格式：tomcat 中，在 Connector 中添加URIEncoding="UTF-8"； 1.2、post 请求乱码 post 请求中，请求参数分两部份， 1.2.1、url？参数，
【Spark十六】： Spark SQL第二部分数据源和注册表的几种方式 bit1129 spark
Spark SQL数据源和表的Schema case class apply schema parquet json JSON数据源准备源数据 {"name":"Jack", "age": 12, "addr":{"city":"beijing&
JVM学习之:调优总结 -Xms -Xmx -Xmn -Xss BlueSkator -Xss -Xmn -Xms -Xmx
堆大小设置JVM 中最大堆大小有三方面限制：相关操作系统的数据模型（32-bt还是64-bit）限制；系统的可用虚拟内存限制；系统的可用物理内存限制。32位系统下，一般限制在1.5G~2G；64为操作系统对内存无限制。我在Windows Server 2003 系统，3.5G物理内存，JDK5.0下测试，最大可设置为1478m。典型设置： java -Xmx355
jqGrid 各种参数详解(转帖) BreakingBad jqGrid
jqGrid 各种参数详解分类：源代码分享个人随笔请勿参考解决开发问题 2012-05-09 20:29 84282人阅读评论(22) 收藏举报 jquery 服务器 parameters function ajax string
读《研磨设计模式》-代码笔记-代理模式-Proxy bylijinnan java 设计模式
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ import java.lang.reflect.InvocationHandler; import java.lang.reflect.Method; import java.lang.reflect.Proxy; /* * 下面
应用升级iOS8中遇到的一些问题 chenhbc ios8 升级iOS8
1、很奇怪的问题，登录界面，有一个判断，如果不存在某个值，则跳转到设置界面，ios8之前的系统都可以正常跳转，iOS8中代码已经执行到下一个界面了，但界面并没有跳转过去，而且这个值如果设置过的话，也是可以正常跳转过去的，这个问题纠结了两天多，之前的判断我是在 -(void)viewWillAppear:(BOOL)animated 中写的，最终的解决办法是把判断写在 -(void
工作流与自组织的关系？ comsci 设计模式工作
目前的工作流系统中的节点及其相互之间的连接是事先根据管理的实际需要而绘制好的，这种固定的模式在实际的运用中会受到很多限制，特别是节点之间的依存关系是固定的，节点的处理不考虑到流程整体的运行情况，细节和整体间的关系是脱节的，那么我们提出一个新的观点，一个流程是否可以通过节点的自组织运动来自动生成呢？这种流程有什么实际意义呢？这里有篇论文，摘要是：“针对网格中的服务
Oracle11.2新特性之INSERT提示IGNORE_ROW_ON_DUPKEY_INDEX daizj oracle
insert提示IGNORE_ROW_ON_DUPKEY_INDEX 转自：http://space.itpub.net/18922393/viewspace-752123 在 insert into tablea ...select * from tableb中，如果存在唯一约束，会导致整个insert操作失败。使用IGNORE_ROW_ON_DUPKEY_INDEX提示，会忽略唯一
二叉树:堆 dieslrae 二叉树
这里说的堆其实是一个完全二叉树,每个节点都不小于自己的子节点,不要跟jvm的堆搞混了.由于是完全二叉树,可以用数组来构建.用数组构建树的规则很简单: 一个节点的父节点下标为: (当前下标 - 1)/2 一个节点的左节点下标为: 当前下标 * 2 + 1 &
C语言学习八结构体 dcj3sjt126com c
为什么需要结构体，看代码 # include <stdio.h> struct Student //定义一个学生类型，里面有age, score, sex, 然后可以定义这个类型的变量 { int age; float score; char sex; } int main(void) { struct Student st = {80, 66.6,
centos安装golang dcj3sjt126com centos
#在国内镜像下载二进制包 wget -c http://www.golangtc.com/static/go/go1.4.1.linux-amd64.tar.gz tar -C /usr/local -xzf go1.4.1.linux-amd64.tar.gz #把golang的bin目录加入全局环境变量 cat >>/etc/profile<
10.性能优化-监控-MySQL慢查询 frank1234 性能优化 MySQL慢查询
1.记录慢查询配置 show variables where variable_name like 'slow%' ; --查看默认日志路径查询结果：--不用的机器可能不同 slow_query_log_file=/var/lib/mysql/centos-slow.log 修改mysqld配置文件：/usr /my.cnf[一般在/etc/my.cnf，本机在/user/my.cn
Java父类取得子类类名 happyqing java this 父类子类类名
在继承关系中，不管父类还是子类，这些类里面的this都代表了最终new出来的那个类的实例对象，所以在父类中你可以用this获取到子类的信息！ package com.urthinker.module.test; import org.junit.Test; abstract class BaseDao<T> { public void
Spring3.2新注解@ControllerAdvice jinnianshilongnian @Controller
@ControllerAdvice，是spring3.2提供的新注解，从名字上可以看出大体意思是控制器增强。让我们先看看@ControllerAdvice的实现： @Target(ElementType.TYPE) @Retention(RetentionPolicy.RUNTIME) @Documented @Component public @interface Co
Java spring mvc多数据源配置 liuxihope spring
转自：http://www.itpub.net/thread-1906608-1-1.html 1、首先配置两个数据库 <bean id="dataSourceA" class="org.apache.commons.dbcp.BasicDataSource" destroy-method="close&quo
第12章 Ajax（下） onestopweb Ajax
index.html <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/
BW / Universe Mappings blueoxygen BO
BW Element OLAP Universe Element Cube Dimension Class Charateristic A class with dimension and detail objects (Detail objects for key and desription) Hi
Java开发熟手该当心的11个错误 tomcat_oracle java 多线程工作单元测试
#1、不在属性文件或XML文件中外化配置属性。比如，没有把批处理使用的线程数设置成可在属性文件中配置。你的批处理程序无论在DEV环境中，还是UAT（用户验收测试）环境中，都可以顺畅无阻地运行，但是一旦部署在PROD 上，把它作为多线程程序处理更大的数据集时，就会抛出IOException，原因可能是JDBC驱动版本不同，也可能是#2中讨论的问题。如果线程数目可以在属性文件中配置，那么使它成为
推行国产操作系统的优劣 yananay windows linux 国产操作系统
最近刮起了一股风，就是去“国外货”。从应用程序开始，到基础的系统，数据库，现在已经刮到操作系统了。原因就是“棱镜计划”，使我们终于认识到了国外货的危害，开始重视起了信息安全。操作系统是计算机的灵魂。既然是灵魂，为了信息安全，那我们就自然要使用和推行国货。可是，一味地推行，是否就一定正确呢？先说说信息安全。其实从很早以来大家就在讨论信息安全。很多年以前，就据传某世界级的网络设备制造商生产的交

pff1_whylog return Nominal Inflation_CPI_Realized Volati_outlier_distplot_Jarque–Bera_pAcf_sARIMAx

Simple returns VS Log returns

What is an inflation rate?

The consumer price index

What Is the Inflation-Adjusted Return?

example

Example of Inflation-Adjusted Return

Nominal Return vs. Inflation-Adjusted Return

Changing frequency

What is Realized Volatility?

Realized Volatility Formula

Examples of Realized Volatility

Advantages

Disadvantages

Limitation

Important Points

Identifying outliers

Simple moving average

Standard deviation

Investigating stylized facts of asset returns

Fact1:Non-Gaussian distribution of returns回报的非高斯(正态)分布

the binomial distribution

Histogram of returns

Q-Q plot

Jarque–Bera test : can give us reason to reject the null hypothesis

The Jarque-Bera test — Example

Skewness(偏度)

Kurtosis(峰度)

Fact2: Volatility clustering

Making a time series stationary

Autocorrelation

Autocorrelation in Technical Analysis

Example of Autocorrelation

10.2 - Autocorrelation and Time Series Methods

(MA) Moving Average Model

Autocorrelation(,,,...,,) and Partial Autocorrelation(and )

Example 1: Google Data

Amazon Announces 20-1 Stock Split

Example 2(PACF:sm.OLS vs AutoReg): Quake Data

From AutoReg to SARIMAX

Fact3: Absence of autocorrelation in returns

Fact 4:Small and decreasing autocorrelation in squared/absolute returns

Fact5: Leverage effect

你可能感兴趣的:(人工智能)

Autocorrelation( $\large y_t$ , $\large y_{t-1}$ , $\large y_{t-2}$ ,..., $\large y_{t-(k-1)}$ , $\large y_{t-k}$ ) and Partial Autocorrelation( $\large y_t$ and $\large y_{t-k}$ )