搜索中的权重度量利器: TF-IDF和BM25

我们在网上搜东西时，搜索引擎总是会把相关性高的内容显示在前面，相关性低的内容显示在后面。那么，搜索引擎是如何计算关键字和内容的相关性呢？这里介绍2种重要的权重度量方法：TF-IDF和BM25。

    在进入理论探讨之前，我们先举个例子。假如，我们想找和“Lucence”相关的文章。可以想一下，那些内容里只出现过一次“Lucence”的文章，有可能是在讲某种技术，顺便提到了Lucence这个工具。而那些出现了两三次“Lucence”的文章，很可能是专门讨论Lucence的。通过直觉，我们可以得出判断：关键字出现的次数越多，文档与关键字的匹配度越高。

 

TF的定义

    有一个专门的术语来表示关键字出现的次数，叫“词频”(Term Frequency), 简写为TF。TF越大，通常相关性越高。

    但是，你可能会发现一个问题。 如果一篇小短文里出现了一次“Lucence”，而一部好几百页的书里提到两次“Lucence”，我们不会认为那部书与Lucence相关性更高。为了消除文档本身大小的影响，一般使用TF时会把文本长度考虑上：

TF Score ＝ 某个词在文档中出现的次数 ／ 文档的长度

举例：某文档D，长度为200，其中“Lucence”出现了2次，“的”出现了20次，“原理”出现了3次，那么:

TF(Lucence|D) = 2/200 = 0.01
TF(的|D) = 20/200 = 0.1
TF(原理|D) = 3/200 = 0.015

 “Lucence的原理”这个短语与文档D的相关性就是三个词的相关性之和。

TF(Lucence的原理|D) = 0.01 + 0.1 + 0.015 = 0.125

    我们发现一个问题，就是“的”这个词占了很大权重，而它对文档主题的几乎没什么贡献。这种词叫停用词，在度量相关性时不考虑它们的词频。去掉这个词后，上面的相关性变为0.025。其中“Lucence”贡献了0.01, “原理”贡献了0.015。

    细心的人还会发现，“原理”是个很通用的词，而“Lucence”是个专业词。直觉告诉我们，“Lucence”这个词对我们的搜索比“原理”更重要。抽象一下，可以理解为 一个词预测主题的能力越强，就越重要，权重也应该越大。反之，权重越小。

    假设我们把世界上所有的文档的总和看成一个文档库。如果一个词，很少在文档库里出现过，那通过它就容易找到目标，它的权重也应该大。反之，如果一个词在文档库中大量出现，看到它仍然不清楚在讲什么内容，它的权重就应该小。“的、地、得”这些虚词出现的频率太高，以至于权重设为零也不影响搜素，这也是它们成为停用词的原因之一。

IDF的定义

    假设关键词w在n个文档中出现过，那么n越大，则w的权重越小。常用的方法叫“逆文本频率指数”(Inverse Dcument Frequency, 缩写为IDF)。一般的：

IDF = log(N/n)

 

注意: 这里的log是指以2为底的对数,不是以10为底的对数。

    N表示全部文档数。假如世界上文档总数位100亿，"Lucence"在1万个文档中出现过，“原理”在2亿个文档中出现过，那么它们的IDF值分别为：

IDF(Lucence) = log(100亿/1万) = 19.93
IDF(原理) ＝ log(100亿/2亿) ＝ 5.64

    “Lucence”重要性相当于“原理”的3.5倍。停用词“的”在所有的文档里出现过，它的IDF=log(1)=0。短语与文档的最终相关性就是TF和IDF的加权求和：

simlarity = TF1*IDF1 + TF2*IDF2 + ... + TFn*IDFn

    现在可以计算出上文中提到的“Lucence的原理”与文档D的相关性:

simlarity(Lucence的原理|D) = 0.01*19.93 + 0 + 5.64*0.015 ＝ 0.2839

 

    其中，“Lucence”占了70%的权重，“原理”仅占30%的权重。

Lucence中的TF-IDF

    早期的Lucence是直接把TF-IDF作为默认相似度来用的，只不过做了适当调整，它的相似度公式为:

simlarity = log(numDocs / (docFreq + 1)) * sqrt(tf) * (1/sqrt(length))

    numDocs:索引中文档数量，对应前文中的N。lucence不是(也不可能)把整个互联网的文档作为基数，而是把索引中的文档总数作为基数。

•     docFreq: 包含关键字的文档数量，对应前文中的n。

•     tf: 关键字在文档中出现的次数。

•     length: 文档的长度。

    上面的公式在Lucence系统里做计算时会被拆分成三个部分：

IDF Score = log(numDocs / (docFreq + 1))
TF Score = sqrt(tf)
fieldNorms = 1/sqrt(length)

   fieldNorms 是对文本长度的归一化(Normalization)。所以，上面公式也可以表示成:

simlarity = IDF score * TF score * fieldNorms

 

BM25, 下一代的TF-IDF

    新版的lucence不再把TF-IDF作为默认的相关性算法，而是采用了BM25(BM是Best Matching的意思)。BM25是基于TF-IDF并做了改进的算法。

BM25中的TF

    传统的TF值理论上是可以无限大的。而BM25与之不同，它在TF计算方法中增加了一个常量k，用来限制TF值的增长极限。下面是两者的公式：

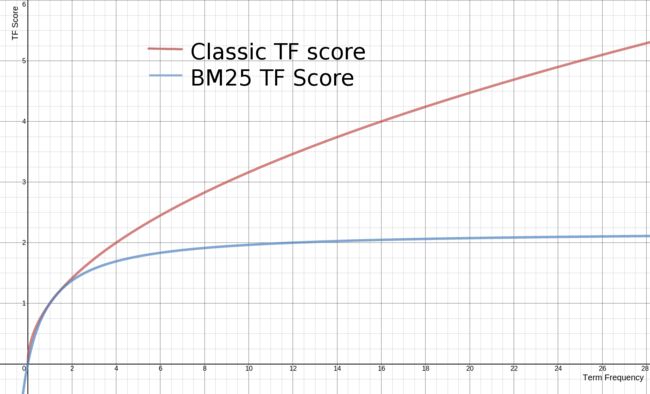
传统 TF Score = sqrt(tf)
BM25的 TF Score = ((k + 1) * tf) / (k + tf)

    下面是两种计算方法中，词频对TF Score影响的走势图。从图中可以看到，当tf增加时，TF Score跟着增加，但是BM25的TF Score会被限制在0~k+1之间。它可以无限逼近k+1，但永远无法触达它。这在业务上可以理解为某一个因素的影响强度不能是无限的，而是有个最大值，这也符合我们对文本相关性逻辑的理解。 在Lucence的默认设置里，k＝1.2，使用者可以修改它。

BM25如何对待文档长度

    BM25还引入了平均文档长度的概念，单个文档长度对相关性的影响力与它和平均长度的比值有关系。BM25的TF公式里，除了k外，引入另外两个参数：L和b。L是文档长度与平均长度的比值。如果文档长度是平均长度的2倍，则L＝2。b是一个常数，它的作用是规定L对评分的影响有多大。加了L和b的公式变为：

TF Score = ((k + 1) * tf) / (k * (1.0 - b + b * L) + tf)

    下面是不同L的条件下，词频对TFScore影响的走势图：

    从图上可以看到，文档越短，它逼近上限的速度越快，反之则越慢。这是可以理解的，对于只有几个词的内容，比如文章“标题”，只需要匹配很少的几个词，就可以确定相关性。而对于大篇幅的内容，比如一本书的内容，需要匹配很多词才能知道它的重点是讲什么。

    上文说到，参数b的作用是设定L对评分的影响有多大。如果把b设置为0，则L完全失去对评分的影响力。b的值越大，L对总评分的影响力越大。此时，相似度最终的完整公式为：

simlarity = IDF * ((k + 1) * tf) / (k * (1.0 - b + b * (|d|/avgDl)) + tf)

 

传统TF-IDF vs. BM25

    传统的TF-IDF是自然语言搜索的一个基础理论，它符合信息论中的熵的计算原理，虽然作者在刚提出它时并不知道与信息熵有什么关系，但你观察IDF公式会发现，它与熵的公式是类似的。实际上IDF就是一个特定条件下关键词概率分布的交叉熵。

    BM25在传统TF-IDF的基础上增加了几个可调节的参数，使得它在应用上更佳灵活和强大，具有较高的实用性。

读者思考

    为什么BM25的TF Score计算要用 d/avgDl, 而不是用平方根、log或者其它计算方法？它背后是否有理论支持？