Make Your First GAN With PyTorch：3.针对手写数字识别网络改进的讨论

本章是 Make Your First GAN With PyTorch 的第 3 章，本书的介绍详见这篇文章。
本章针对的 神经网络 是指在本书第 2 章建立的数字分类的网络，该网络详见 这篇文章。

---

---

本书的上一章开发了一个神经网络来对手写数字的图像进行分类，虽然网络设计简单，但效果不错，使用 MNIST 测试数据集获得了 87% 的准确性。

这章主要是探索针对网络不同方面的改进方式，用于改进网络的性能，同时加深对网络的理解。

回顾一下神经网络的几个要素，除了网络结构外，能想到的包括 损失函数、激活函数、参数优化方法 几个，下面主要是对这几个要素进行改进。
除了这几个要素外，还包括信号的 规范化 （后面会详细说明）。

1. 损失函数

一些神经网络，是为了产生连续范围的输出值，比如温度预测网络要求能输出 0 到 100 摄氏度的任意数值；还有一些网络是为了产生 True/False 或 1/0 的输出，比如某个用于辨别图像是否是猫的网络，需要输出值接近 0.0 或 1.0， 而非其他值。

如果对不同场景下的损失函数进行分析，可以发现第一种任务，也就是所谓的 回归（regression） 任务，可以使用 均方误差(Mean Squared Error, MSE） 损失；

对于第二种分类任务，则更适用其他损失函数，一个常用的损失函数为 二元交叉熵（Binary Cross Entropy），该函数的初衷是惩罚 “错误但确信” 的输出，以及 “正确但不太确信” 的输出。PyTorch 提供了该损失函数为 nn.BCELoss()。

本文讨论的网络，用于 MNIST 图像分类的网络，属于第二种类型，输出节点的值理想状态，除了一个确信的结果输出接近 1.0 之外，其他的应接近 0.0 。

将前面网络的 notebook 文件并将损失函数从 MSELoss() 修改为 BCELoss()：

self.loss_function = nn.BCELoss()

对该网络仍然使用 3 个 epochs 进行训练，性能分数变为 91%，相比之前 87% 进步不小。

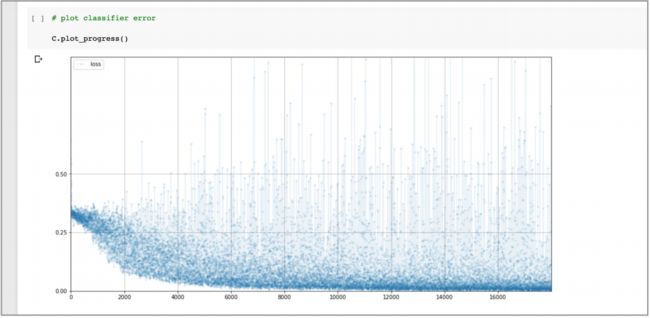
有趣的是观察损失图表：

• 可以看到，损失值确实下降了，但是开始阶段，相比 MSELoss() 下降地更缓慢，损失值噪声也更大，甚至在训练的后面也可偶尔有较大的值。
• 虽然这个损失图表可能看起来比前面的更差，但是训练的末端大多数损失值更小，同时更好的性能分数也反映出这个损失值更好。

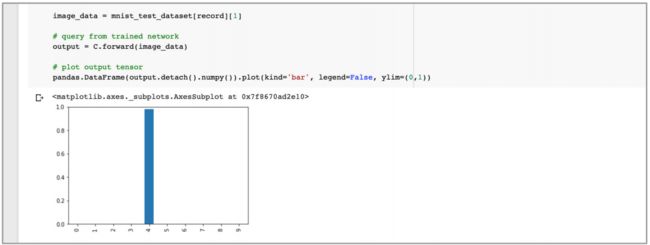
下面的图像再次反映了训练数据集第 19 个记录的输出值：

可以看到网络更相信图像是数字 4，而且对图像是数字 9 的信心更低了。

2. 激活函数

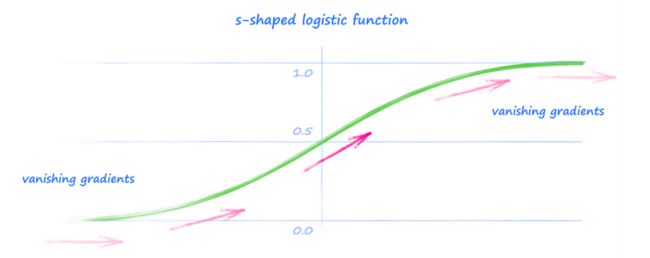
早期的神经网络使用的是 s-型 Logistic 函数，因为它的形状与动物真实神经元传递信号的方式更加类似，而且在计算梯度时数学上更方便。

但是，该函数也有一些弱点。最主要的是对较大的数（上图右端），梯度（导数）会很小， 甚至可能事实上消失。由于神经网络的训练依赖梯度来修正连接权重，可能在这种 饱和(saturation) 发生时而失效。

为了避免上述问题，还有很多可供选择的激活函数，其中一个简单的直线就可以解决这个问题，直线修正后的梯度并不会消失。

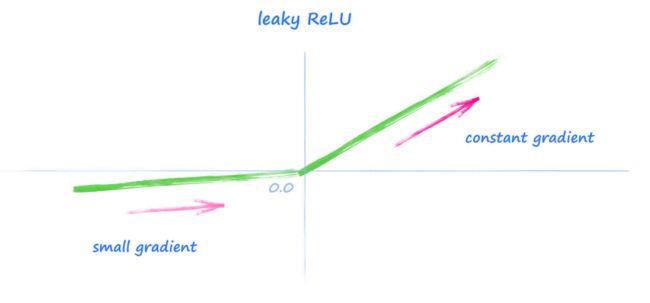
该激活函数称为 线性整流单元(Rectified Linear Unit，ReLU)，而且 PyTorch 也提供了一个 ReLU() 函数供直接使用。

但是观察上图，由于小于 0 的值的斜率为 0，这可能导致小于 0 的信号会产生梯度消失的问题。一个简单的方法是在函数左侧增加一个小梯度，称为 Leaky ReLU。

将之前的网络 的损失函数重置为 MSELoss() ，然后改变激活函数为 LeakyReLU(0.02)。其 中 0.02 是函数左侧的梯度值。

# 定义神经网络各层
self.model = nn.Sequential(
    nn.Linear(784, 200),
    nn.LeakyReLU(0.02),
    nn.Linear(200, 10),
    nn.LeakyReLU(0.02)
)

再次训练 3 epochs。本书的例子，性能分数为 97%，相比之前 87% 进步非常大，接近了使用更复杂网络的行业领先水平。

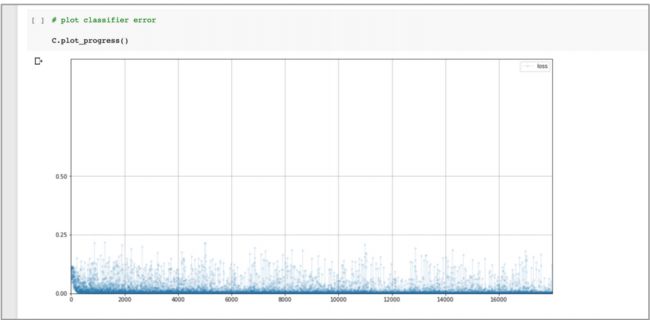
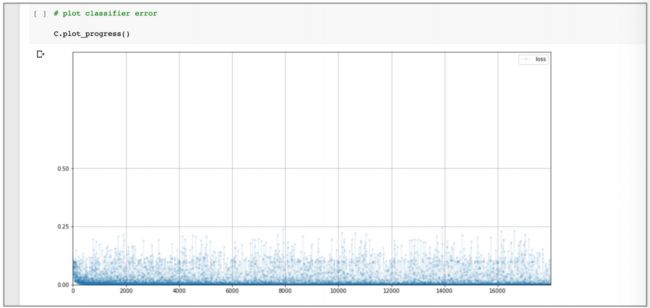
对应的损失值图表见下图：

可以看到损失值很快下降到接近 0，而且在训练的初期，平均的损失值也很小， 而且噪声值也较低。

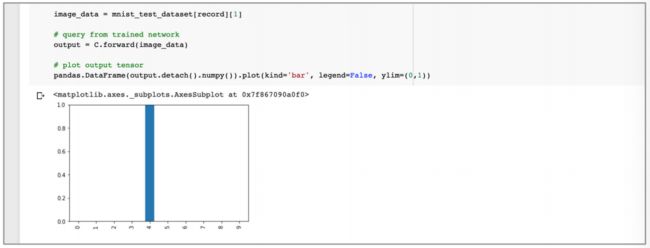
对训练数据集第 19 个记录的输出值而言，该网络非常确信图像是 4，而且所有 其他节点的值非常接近 0。

• 本节的讨论可以看到，改变激活函数会产生意义重大的影响，简单而言，是因为更好的梯度值。

3. 优化方法

我们也可以通过改进反向传播梯度技术来更新网络的权重。
前面的网络使用的一个相当简单的方法，随机梯度下降法(stochastic gradient descent)，这个方法很简单，对计算机资源占用度低，所以很流行。

但是随机梯度下降法的一个缺点是可能陷在随机函数的局部极小值，另一个缺点则是对所有的可学习参数使用了相同的学习率。

除了随机梯度下降法外，有一些其他常用的优化方法，比如 Adam 方法，该方法直接解决了这两个挑战。它利用动量的概念来减少陷入局部极小值的机会，这有点像一个重球如何通过一个小坑，因为它的动量能使它顺利通过这些小坑；该方法还为每个可学习参数使用了单独的学习速率，以适应每个参数在训练过程中的变化。

• Pytorch 中常用的优化方法介绍，可以参见这篇博文。

将原代码返回为使用 MSELoss() 和 sigmoid 激活函数的版本，然后将优化器从 SGD 改变为 Adam：

self.optimiser = torch.optim.Adam(self.parameters())

再次训练 3 epochs。对我而言，性能分数也是大约 97%，相比之前 87% 进步很 大，而且与使用 LeakyReLU 激活函数的改进类似。检查一下损失图表如下图。

看起来 Adam 优化器相当有效，损失值很快地下降到 0 附近，而且平均值也保持在低位。

同样的，下图显示，对训练数据集第 19 个记录的输出值显示出该网络有很高的信心水平认为图像是一个数字 4。

• 总体来看，虽然并不完美，但 Adam 对很多任务而言，可谓是一个不错的选择。

4. 规范化（Normalisation）

神经网络中的权重，和穿过网络的信号，可能具有潜在很大的值。前面提到，这些很大的值可能导致饱和。

现在已经有大量研究，用以减少神经网络中参数和信号值的范围，并且还对值进行搬移以使平均值为 0，这称之为 规范化 (Normalisation)。

将代码复原到使用 MSELoss，sigmoid 激活函数和 SGD 优化器的版本，然后使用 LayerNorm(200) 来对进入到最终层之前的网络信号进行规范化：

# 定义神经网络各层
self.model = nn.Sequential(
    nn.Linear(784, 200),
    nn.LeakyReLU(0.02),
    
    nn.LayerNorm(200),
    
    nn.Linear(200, 10),
    nn.LeakyReLU(0.02)
)

再次训练该网络 3 epochs，使用测试数据的性能分数也是 91%，与原始网络的 87% 相比，改进也不错。观察损失图表：

可以看到损失的下降速度比原始网络更快，而且那么则损失的噪声也不那么多。

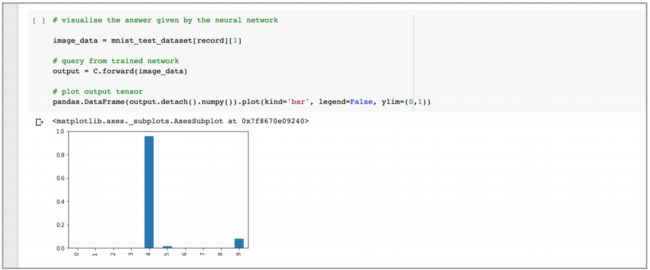
关注下图：

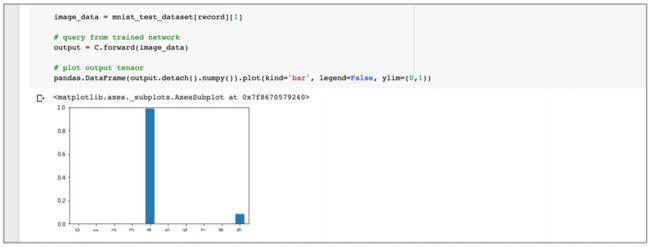
还可以看到，该网络的输出要干净得多，其中既有数字 4 的非常有把握的值，但也有数字 9 的较小且可以理解的值，同时与原始网络不同，其它值基本上为 0。

• 需要注意的是，即使到现在，规范化为什么可以帮助神经网络的训练的准确原因还没有完全确定，还在出现新的研究文章，提供不同的研究角度。

5. 综合改进

对本文使用过的改进进行综合，综合使用 BCE 损失，LeakyReLU 激活函数，Adam 优化器和网络规范化。

• 由于 BCE 损失只能接受在 0 和 1 范围之内的值。但是 LeakyReLU 的输出值可能超出这个范围。 因此，最后一层后改为使用 sigmoid 函数，但在隐藏层保持使用 LeakyReLU 激活函数。

# 定义神经网络各层
self.model = nn.Sequential(
    nn.Linear(784, 200),
    nn.LeakyReLU(0.02),
    
    nn.LayerNorm(200),
    
    nn.Linear(200, 10),
    nn.Sigmoid()
)

训练该网络 3 epochs，性能分数大约为 97%。 看起来将所有的技巧合并使用，并不能给出超过 97% 的准确率。为了获得世界级的分数，这个简单的网络已经不足以使用了，需要更复杂的网络结构，后面会进行介绍。

6. 要点总结

结合本文和构建网络的文章，总结如下要点：

• 实践证明，使用新数据或构建新的工作流程时，最好对数据预览(pre­view)来保证数据正确载入和变换；

• PyTorch 可以完成机器学习任务中很多工作。为了利用这个优势，我们需要和 PyTorch 的机制合作，比如，神经网络需要从 PyTorch 的 nn.Module 的类中导出；

• 均方误差(Mean Squared Error) 损失值适合于回归任务，这类任务的输出是连续值；而二元交叉熵(Binary Cross Entropy) 损失值对输出可能为 1 或 0，True 或 False 的分类任务更为适合；

• 传统的 sigmoid 激活函数对大的输出值可能出现 梯度消失(vanishing gradients)，导致训练网络时反馈信号不佳；ReLU 激活函数通过对正的输入有良好的梯度值，解决了这个问题；LeakyReLU 对负值提供了一个小的非消失梯度值来进行进一步改进；

• Adam 优化器使用了动量来改进局部极小值，并保证每个可学习参数的学习率不同。对很多任务而言，它的效果比简单的 SGD 优化器更好；

• 规范化(Normalisation) 可以稳定神经网络的训练。对网络的初始权重进行规范化很常见，当信号值通过具有 LayerNorm 的神经网络时，将其规范化可以提高性能。