GAN 的理想损失值应该是多少?(Make Your First GAN With PyTorch 附录 A)
本文是 Make Your First GAN With PyTorch 的附录 A,本书的介绍详见这篇文章。
在神经网络训练中,损失值可用于衡量网络的效果,也对网络的训练至关重要。 专栏中讨论过理想 GAN 的损失值,但不同损失值不同,本文就使用 均方误差(MSE)损失 和 二进制交叉熵(BCE) 对 GAN 的理想损失值进行探讨。
本文目录
- 1. 均方误差损失值(MSE)
- 2. 二进制交叉熵损失值(BCE)
-
- 2.1 从概率说起
- 2.2 熵是什么?
- 2.3 交叉熵
- 2.4 二进制交叉熵
前面的专栏文章中,多次提到 GAN 训练的理想状态是在生成器和鉴别器之间达到平衡。
- 这样,鉴别器 不再能 区分实际数据和生成的数据,这是因为生成器已经从真实数据中学习创造看起来真实的数据。
下面来计算鉴别器在达到平衡时,损失值应该是怎样的。我们同时对 均方误差 (Mean Squared Error, MSE) 和 二进制交叉熵(Binary Cross Entropy) 的损失值进行计算。
1. 均方误差损失值(MSE)
均方误差损失值的定义很简单,数学定义如下:
l o s s = 1 n ∑ n ( t − o ) 2 loss = \frac{1}{n} \sum_n (t - o)^2 loss=n1n∑(t−o)2
其中,对 n n n 个输出节点,实际的输出为 o o o,预期的输出目标为 t t t。
- 简单看,由于单纯的 误差(error) 是输出节点的值和预期目标值的差值,可以为正数或负数。
- 而通过将误差求平方,这个值就一直是正数了,MSE 是这些误差平方的平均值。
对 GAN 而言,由于鉴别器仅有一个节点,上式可以简化为:
l o s s = ( t − o ) 2 loss = (t - o)^2 loss=(t−o)2
- 如果鉴别器完全 不能 分辨真实数据和生成的数据,上式将输出 0,这意味着它有十足把握认为数据是真实的;
- 如果上式输出的是 1,这说明鉴别器有十足把握认为数据是生成的;
如果上式的输出为 0.5 ,意味着鉴别器 没有信心 分辨数据是真实的,或者是生成器生成的。
- 前面提到,这就是 GAN 的理想状态。
当目标值为 1 而输出为 0.5 时,单纯的 误差(error) 为 0.5;类似的,当目标值为 0 时, 单纯的 误差(error) 值也为 0.5。
- 由于 MSE 是对误差值求平方,上面两个 误差(error) 对应的 MSE 值均为 0.25。
所以 平衡的 GAN 对应的均方误差值(MSE)是 0.25。
2. 二进制交叉熵损失值(BCE)
二进制交叉熵损失值(Binary Cross Entropy, BCE)基于可能性和不确定性的概念,让我们一步步的说明。
2.1 从概率说起
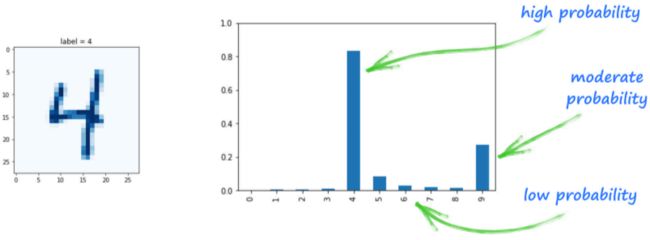
考虑 MNIST 分类器,该网络有 10 个输出节点,每个节点对应一个可能的分类。
如果已训练好的分类器网络认为某个图像是数字 4,那么第四个输出节点将有较高的输出, 其他的节点输出值则较小。
- 之前探讨过,这些值可以认为是分类的信心指标,同时由于输出节点的值仅在 0 和 1 之间,我们可以简单将这些值看做 概率(probabilities)。
- 该网络在 第四个节点 输出较高的值,意味着网络认为该图像有很大可能是数字 4;
- 网络也给 第九个节点 分配了中等大小的值,说明网络认为该图像可能为数字 9;
- 另外,网络给其他节点分配了很低的值,因为网络认为这个图像看起来并不像其他数字。
- 那么,一个优秀的 损失值 应当是什么样的呢?
观察下面的表格,显示了节点输出值 x 和预期输出值 y 的例子:
| 输出(output) x | 目标(target) y | 注释 |
|---|---|---|
| 0.9 | 1.0 | 几乎正确 |
| 0.1 | 1.0 | 非常错误 |
- 第一行中,神经网络分类结果输出为 0.9 ,而目标值是 1.0,所以可以认为分类是 几乎正确 的。 对于一个好的损失函数而言,这个输出的损失值应很小。
- 第二行中,分类结果的值很小,为 0.1,而目标值为 1.0,所以网络的这个输出非常错误。 对于一个好的损失函数而言, 这个输出的损失值应该是很大的。
- 下面我们从概率转移到 不确定性。
2.2 熵是什么?
熵(Entropy) 是用来形容不确定性的数学概念。
- 如果有硬币两面都是 “字”,那 么我们掷硬币获得 “字” 的几率就是 100%,获得 “花” 的几率就是 0%。这种情况下,每次掷硬币的结果都是 100% 确定的,不确定性是 0,所以我们认为熵是 0;
- 如果硬币是正常的,一面是 “字”,一面是 “花”,掷硬币的结果是最不确定的, 熵也就是最高的。
熵的数学定义如下所示:
e n t r o p y = ∑ − p ⋅ l n ( p ) entropy = \sum -p \cdot ln(p) entropy=∑−p⋅ln(p)
上式中,使用求和遍历了所有可能的结果,而 p p p 是每个结果的概率。
- 我们不去深究这个表达式的来源,而用可视化的方式观察为什么这个表达式是正确的。
针对掷硬币获得 “字” 的概率,下图显示了由上面表达式计算的熵:
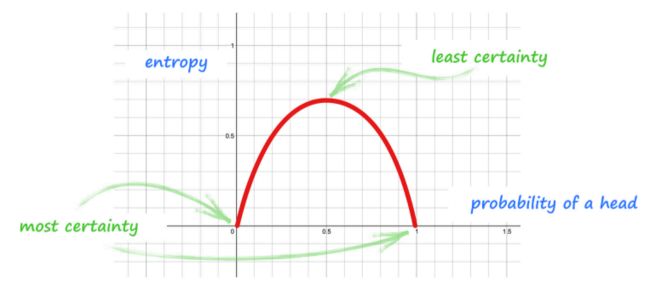
这个图的横轴是掷硬币获得 “字” 的概率(probability of a head),纵轴则是 熵(entropy):
- 如果,硬币的两面都是 “字(head)”,所以 p ( h e a d ) = 1 p(head)=1 p(head)=1,不确定性是 0;
- 如果,硬币两面都是 “花(tail)”,那么 p ( h e a d ) = 0 p(head)=0 p(head)=0,不确定性同样是 0;
- 如果,硬币是正常的,那么 p ( h e a d ) = 0.5 p(head)=0.5 p(head)=0.5,这时的熵是最高的。
看完原理后,我们对硬币两面都是 “字” 的情况(也就是 p ( h e a d ) = 1 p(head)=1 p(head)=1)进行计 算:
e n t r o p y = ∑ − p ⋅ l n ( p ) = − 1 ⋅ l n ( 1 ) − 0 ⋅ l n ( 0 ) = 0 entropy = \sum -p \cdot ln(p) = -1 \cdot ln(1) - 0 \cdot ln(0) = 0 entropy=∑−p⋅ln(p)=−1⋅ln(1)−0⋅ln(0)=0
上面式子中,计算了掷硬币结果是 “字” 和 “花” 的所有情况。
- 由于硬币两面都是 “字”,所以掷硬币结果是 “字” 的概率为 1,是 “花” 的概率为 0;
- 由于 l n ( 1 ) ln(1) ln(1) 等于 0,而 0 ⋅ l n ( 0 ) 0 \cdot ln(0) 0⋅ln(0) 中即使 l n ( 0 ) ln(0) ln(0) 无定义,也很容易得到结果是 0。
所以式子计算的结果与上图中 p ( h e a d ) = 1 p(head)=1 p(head)=1 时熵为 0 的结果一致。
对于一个正常的硬币,由于 p ( h e a d ) = 0.5 p(head)=0.5 p(head)=0.5 而且 p ( t a i l ) = 0.5 p(tail)=0.5 p(tail)=0.5,完成熵的计算,获得最大熵的值。
2.3 交叉熵
从上一节看到,熵是表述输出不确定性的一个方法。
而 交叉熵(cross entropy),是对由于实际输出的可能性与我们认为
的可能性之间区别而产生不匹配,而产生的输出不确定性的一个指标。
上面这句话听起来很抽象,让我们回到硬币的例子来说明。
- 如果我们认为硬币是正常的,但是实际上硬币并不正常,我们就会被掷硬币的结果所震惊,将会有一些有关这些掷硬币结果不确定性,这也是交叉熵所关心的内容。
- 如果我们认为硬币是正常的,实际上它也是正常的,我们将不会被掷硬币结果所震惊,交叉熵将会很低。
所以,我们可以认为交叉熵是两个概率分布之间的一个比较,如果两个分布越匹配,交叉熵就越低;相反,如果两个概率分布完全比配,那么交叉熵就为 0。
那交叉熵和神经网络有什么关系呢?
由于网络的目标输出和实际输出都是概率分布:
- 如果两个分布不同的话,交叉熵将会很高;
- 如果两个分布相近,交叉熵将会很低。
这也是我们希望损失函数所完成的。
下面的表达式从数学上定义了交叉熵:
c r o s s e n t r o p y = ∑ − y ⋅ l n ( x ) crossentropy = \sum - y \cdot ln(x) crossentropy=∑−y⋅ln(x)
上式的求和是对所有可能的分类进行,其中 x x x 是观测到的各分类的概率,而 y y y 是各分类的实际概率。
使用前面的神经网络的例子进行计算,对实际输出 x x x 概率为 0.9,但是期望输出概率为 1.0 的情况,对所有可能的分类概率(也就是 1.0 和 0.0)求和:
c r o s s e n t r o p y = ∑ − y ⋅ l n ( x ) = − 1 ⋅ l n ( 0.9 ) − 0 ⋅ l n ( 1 − 0.9 ) = 0.105 crossentropy = \sum - y \cdot ln(x) = -1 \cdot ln(0.9) - 0 \cdot ln(1-0.9) = 0.105 crossentropy=∑−y⋅ln(x)=−1⋅ln(0.9)−0⋅ln(1−0.9)=0.105
同样的,对另一个实际输出概率为 0.1,但期望为 1.0 的情况进行计算:
c r o s s e n t r o p y = ∑ − y ⋅ l n ( x ) = − 1 ⋅ l n ( 0.1 ) − 0 ⋅ l n ( 1 − 0.1 ) = 2.303 crossentropy = \sum - y \cdot ln(x) = -1 \cdot ln(0.1) - 0 \cdot ln(1-0.1) = 2.303 crossentropy=∑−y⋅ln(x)=−1⋅ln(0.1)−0⋅ln(1−0.1)=2.303
下标是这些结果的总结,我增加了额外的一行:
| 输出(output) x | 目标(target) y | 交叉熵(cross entropy) |
|---|---|---|
| 0.9 | 1.0 | 0.105 |
| 0.1 | 1.0 | 2.303 |
| 0.9 | 0.0 | 2.303 |
- 前两行显示出对非常错误的输出,交叉熵将会更大,而对正确的输出,交叉熵 将会更小。第 3 行则显示出很确定但是错误的输出对应的交叉熵同样很高,这也是可以将交叉熵用于损失函数的重要原因。
- 但是为什么我们要使用这个更加复杂的方法作为损失函数呢?明明 MSE 损失值 的计算更简单、更易理解。
严格来说,我们可以用任何损失函数来惩罚错误的输出。某些人可能偏向使用交叉熵,关键的原因是它更强烈的惩罚错误的输出。
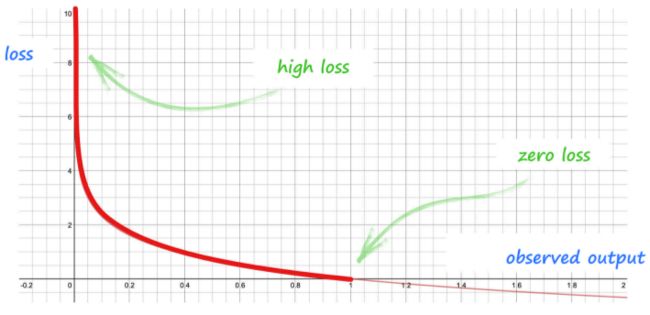
下图显示了期望值为 1.0 的情况下,对不同的观测输出使用交叉熵计算获得的 损失值图表:
- 上图很明确,交叉熵对非常错误的输出能有非常大的损失值,也有更大的导数,可以给神经网络提供了更强的反馈。
2.4 二进制交叉熵
二进制交叉熵(Binary Cross Entropy, BCE) 是仅有两个分类的交叉熵,这种情况也是鉴别器输出分类为真实的 1.0 和虚假的 0.0。
- 让我们回答最初的问题,当鉴别器和生成器平衡时,二进制交叉熵的理想损失值应为多少呢?
当鉴别器在对真实和生成的数据分类同样坏时,其输出将总为 0.5,也就是这些 输出一些为 1.0,另一些为 0.0。
对于 x = 0.5 x=0.5 x=0.5 和 y = 1.0 y=1.0 y=1.0,计算交叉熵:
c r o s s e n t r o p y = ∑ − y ⋅ l n ( x ) = − 1 ⋅ l n ( 0.5 ) − 0 ⋅ l n ( 1 − 0.5 ) = 0.693 crossentropy = \sum - y \cdot ln(x) = - 1 \cdot ln(0.5) - 0 \cdot ln (1 - 0.5) = 0.693 crossentropy=∑−y⋅ln(x)=−1⋅ln(0.5)−0⋅ln(1−0.5)=0.693
对于 x = 0.5 x=0.5 x=0.5 和 y = 0.0 y=0.0 y=0.0,计算交叉熵:
c r o s s e n t r o p y = ∑ − y ⋅ l n ( x ) = − 0 ⋅ l n ( 0.5 ) − 1 ⋅ l n ( 1 − 0.5 ) = 0.693 crossentropy = \sum - y \cdot ln(x) = - 0 \cdot ln(0.5) - 1 \cdot ln (1 - 0.5) = 0.693 crossentropy=∑−y⋅ln(x)=−0⋅ln(0.5)−1⋅ln(1−0.5)=0.693
- 所以,在 GAN 使用
BCELoss()时,理想损失值应该为 0.693。