NMI(Normalized Mutual Information)

NMI(Normalized Mutual Information)

NMI(Normalized Mutual Information)，归一化互信息。常用在聚类中，度量两个聚类结果的相近程度（通常我们都是将聚类结果和真实标签进行比较相似程度）。他的值域是$[0,1]$，值越高表示两个聚类结果越相似。归一化是指将两个聚类结果的相似性值 定量到0~1之间。

NMI和另一个聚类指标ACC不同的是，NMI的值不会受到族类标签排列的影响。(This metric is independent of the absolute values of the labels: a permutation of the class or cluster label values won’t change the score value in any way.) sklearn包实现

公式

$$NMI(Y,C)=\frac{2\times I(Y;C)}{H(Y)+H(C)}$$

其中，

• Y 代表 数据真是的类别；
• C 代表 聚类的结果；
• $H(.)$ 代表 交叉熵, $H(X)=-{\sum }_{i=1}^{|X|}P(i)\log P(i)$。此处的$\log$是以2为底的；
• $I(Y;C)$ 代表 互信息，$I(Y;C)=H(Y)-H(Y|C)$。互信息是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。简明的说就是，表示两个时间集合的相关性。

例子

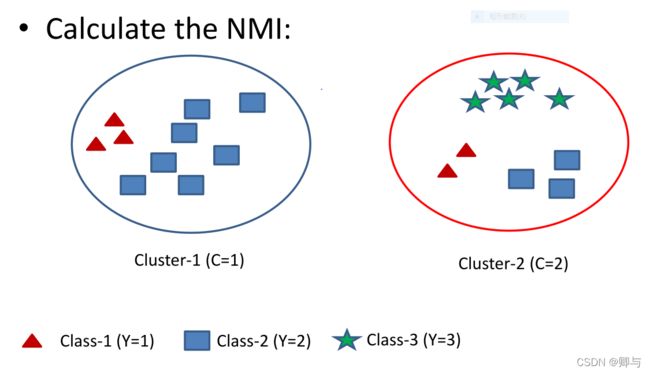
假设我们有3个类别，我们的聚类结果分成了2类，如下图。

1. 计算Y的交叉熵：

$P(Y=1)=5/20=1/4$,

$P(Y=2)=5/20=1/4$,

$P(Y=3)=10/20=1/2$,

$H(Y)=-\frac{1}{4}\log (\frac{1}{4})-\frac{1}{4}\log (\frac{1}{4})-\frac{1}{2}\log (\frac{1}{2})=1.5$。

H(Y) 表示数据真实标签的交叉熵，它是一个固定的值。可以再聚类之前计算出。

2. 计算C的交叉熵：

$P(C=1)=10/20=1/2$,

$P(C=2)=10/20=1/2$,

$H(C)=-\frac{1}{2}\log (\frac{1}{2})-\frac{1}{2}\log (\frac{1}{2})=1$.

H© 表示数据聚类后标签的交叉熵。显然，每次得到一个聚类结果后我们都需要计算一下。

3. 计算Y和C的互信息：

$I(Y;C)=H(Y)-H(Y|C)$。表示两个聚类结果的相近程度。

• C = 1时，

  $P(Y=1|C=1)=3/10$,

  $P(Y=2|C=1)=3/10$,

  $P(Y=3|C=1)=4/10$.

$$
\begin{aligned}

H(Y|C=1) &= -P(C=1)\sum_{y\in {1,2,3}} P(Y=y|C=1)\log P(Y=y|C=1) \
&= -\frac{1}{2} \times[\frac{3}{10}\log(\frac{3}{10}) - \frac{3}{10}\log(\frac{3}{10}) - \frac{4}{10}\log(\frac{4}{10})] \
&= 0.7855

\end{aligned}
$$

• C = 2时，

  同理$H(Y|C=2)=0.5784$

所以 $I(Y;C)=H(Y)-H(Y|C)=1.5-(0.7855+0.5784)=0.1361$

4. 计算Y和C的归一化互信息，即NMI:

$NMI(Y,C)=\frac{2\times I(Y;C)}{H(Y)+H(C)}=\frac{2\times 0.1361}{1.5+1}=0.1089$

另一个例子

数据真实标签如图形，聚类结果分成了两类。

结果是：$NMI(Y,C)=0.2533$