相机标定（五）—— 相机模型详细介绍

---

相机与图像的一些基本概念

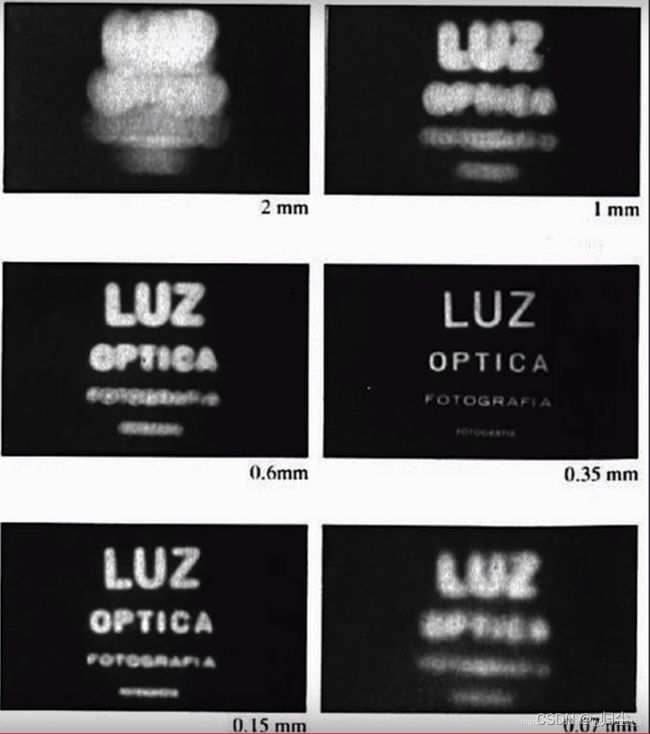
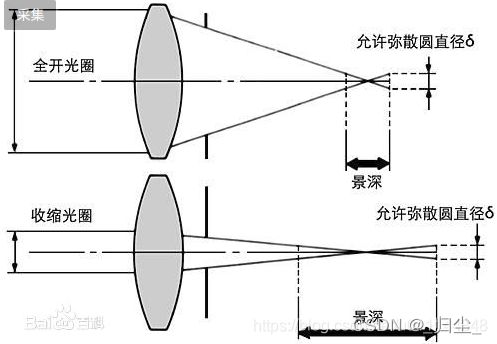
光圈（Aperture）与景深（Depth of Field）：光圈可以看做是小孔成像模型中的孔径，光圈越大进光面积就会越大。

光圈越小，景深越大，但光圈太小会产生衍射现象，如下图。

下图展示了光圈和景深的关系：

视野（Field of View）

$$\theta =arctan(\frac{d}{2}/f)$$
视野取决与两个因素：成像平面(Sensor)的大小、焦距。焦距越大视野越小。

针孔相机模型

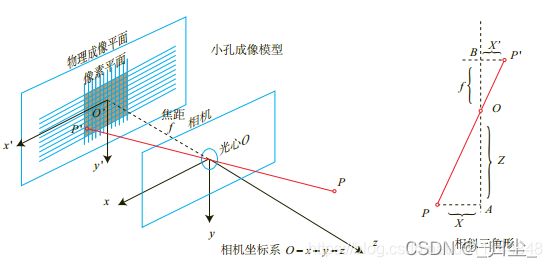
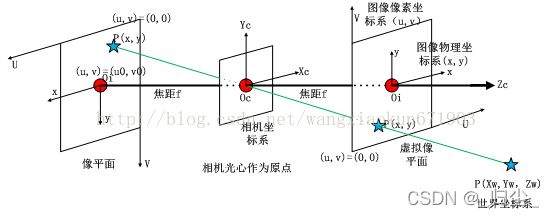
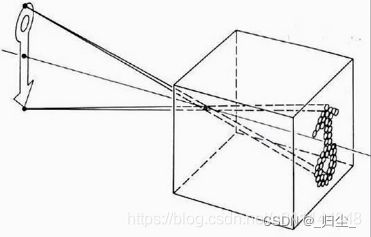
透视投影（Perspective Projection）是最常用的成像模型，可以用针孔成像模型来近似表示。透视投影成像模型的特点是所有来自场景的光线均通过一个投影中心，它对应于透镜的中心，经过投影中心且垂直于图像平面（成像平面）的直线称为投影轴或光轴。

相机的镜头是一组透镜，当平行于主光轴的光线穿过透镜时，会聚到一点上，这个点叫做焦点，焦点到透镜中心的距离叫做焦距$f$。数码相机的镜头相当于一个凸透镜，感光元件就处在这个凸透镜的焦点附近，将焦距近似为凸透镜中心到感光元件的距离时就成为小孔成像模型。

坐标系介绍

世界坐标系

世界坐标系是客观三维世界的绝对坐标系，也称客观坐标系。因为数码相机安放在三维空间中，我们需要世界坐标系这个基准坐标系来描述数码相机的位置，并且用它来描述安放在此三维环境中的其他任何物体的位置，用$（X_w,Y_w,Z_w）$表示其坐标值，单位是长度单位。

相机坐标系（光心坐标系）

相机坐标系是以相机的光心为坐标原点，$X$轴和$Y$轴分别平行于图像坐标系的$X$轴和$Y$轴，相机的光轴为$Z$轴，用$（X_c,Y_c,Z_c）$表示其坐标值，单位是长度单位。

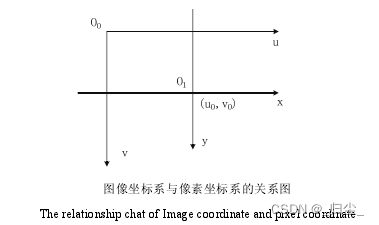
图像坐标系

以CCD图像平面的中心为坐标原点，或者说以主光轴和图像平面交点为坐标原点，$X$轴和$Y$轴分别平行于图像平面的两条垂直边，用$（x,y）$表示其坐标值，单位是长度单位。图像坐标系是用物理单位（例如毫米）表示像素在图像中的位置，也叫图像物理坐标系。

像素坐标系

以CCD图像平面的左上角顶点为原点，$X$轴和$Y$轴分别平行于图像坐标系的$X$轴和$Y$轴，用$（u,v）$表示其坐标值，单位以像素计。数码相机采集的图像首先是形成标准电信号的形式，然后再通过模数转换变换为数字图像。每幅图像的存储形式是$M\ast N$的数组，$M$行$N$列的图像中的每一个元素的数值代表的是图像点的灰度。这样的每个元素叫像素，像素坐标系就是以像素为单位的图像坐标系，也叫图像像素坐标系。

CCD 是英语 Charge Coupled Device（电荷耦合元件）的缩写，是一种将图像转换为电信号的半导体元件。大小约为长宽各 1 厘米左右，由类似棋盘的格状排列的小像素 (pixel) 组成。

用相机拍摄风景时，拍摄对象发出的光通过镜头在 CCD 上成像。光到达 CCD 的某个像素时，将根据光的强度产生相应的电荷。将该电荷的大小读取为电信号，即可获得各像素上光的强度（浓度值）。

换言之，每个像素都是一个可以检测光强度的传感器（光电二极管）。所谓 200 万像素 CCD 就是一个由 200 万个光电二极管构成的集合体。

除了CCD之外，摄像头的传感器还有CMOS（Complementary Metal-Oxide Semiconductor，金属氧化物半导体元件）和CIS（Contact Image Sensor，接触式图像传感器）等类型。

图像在计算机中以矩阵形式存储（二维数组） ，需要对感光度量化成数值，例如0~255之间的整数（彩色图像还有通道） 。

成像过程的数学模型

世界坐标系—>相机坐标系—>图像坐标系—>像素坐标系

世界坐标系->相机坐标系

从世界坐标系到相机坐标系的，为刚体变换，反应了物体与相机的相对运动关系。$P_w(X_w,Y_w,Z_w)-->P_c(X_c,Y_c,Z_c)$
$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$
有6个自由度，这6个参数称为相机的外参（Extrinsic）。

式中，$R$为$3\ast 3$的正交旋转矩阵，$t$为三维平移向量。
在三维空间中，旋转可以分解为绕各自坐标轴的二维旋转，如果依次绕$x,y,z$轴旋转角度，则旋转可以表示为：
$$R_x(\alpha )=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\alpha & sin\alpha \\ 0& -sin\alpha & cos\alpha \end{array}\right]$$

$$R_y(\beta )=\left[\begin{array}{ccc}cos\beta & 0& -sin\beta \\ 0& 1& 0\\ sin\beta & 0& cos\beta \end{array}\right]$$

$$R_z(\gamma )=\left[\begin{array}{ccc}cos\gamma & sin\gamma & 0\\ -sin\gamma & cos\gamma & 0\\ 0& 0& 1\end{array}\right]$$

旋转矩阵$R$可以表示为$R_x,R_y,R_z$的乘积，因此$R=R_x(\alpha )\ast R_y(\beta )\ast R_z(\gamma )$.
$t$平移向量表示摄像机坐标原点在世界坐标系中的位置。

相机坐标系–>像平面坐标系（图像坐标系）

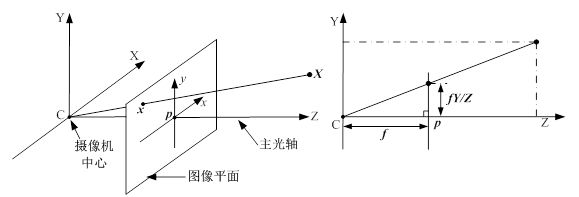
图像坐标系与相机坐标系的转换为：
$$\begin{gathered} x=\frac{f{X}_c}{Z_c} \\ y=\frac{f{Y}_c}{Z_c} \end{gathered}$$
其中$f$为焦距（像平面与相机坐标系原点的距离）。用齐次坐标系和矩阵表示上述关系：
$$Z_c\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]$$
从相机坐标系到图像坐标系的投影只和相机的焦距$f$有关，一个自由度。

图像坐标系–>像素坐标系

图像坐标系与像素坐标系的关系如图。

他们之间的转换关系为：
$$\begin{gathered} u=\frac{x}{dx}+u_0 \\ v=\frac{y}{dy}+v_0 \end{gathered}$$

采用齐次坐标再用矩阵形式将上式表示为：
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{dx}& 0& u_0\\ 0& \frac{1}{dy}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$
其中$（u_0,v_0）$是图像坐标系原点在像素坐标系中的坐标，$dx$ 和 $dy$分别是每个像素在图像平面$x$和 $y$方向上的物理尺寸。从图像坐标系到像素坐标系转换有4个自由度。

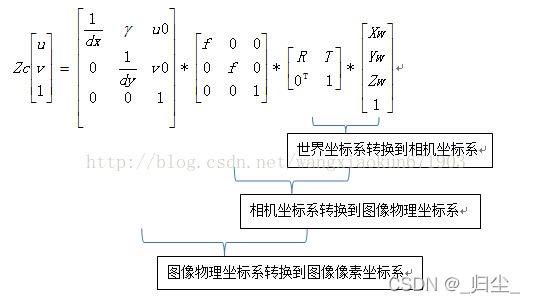
世界坐标系->像素坐标系

$$Z_c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{dx}& 0& u_0\\ 0& \frac{1}{dy}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$
由上式可知，该模型中，内参有5个，外参有6个。
如果把$\frac{1}{dx}$和$\frac{1}{dy}$和$f$相乘得到常用的$f_x,f_y$，则内参有4个自由度，外参有6个自由度（3个旋转，3个平移）。
$$\begin{gathered} Z_c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{dx}& 0& u_0\\ 0& \frac{1}{dy}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}f& 0& 0& 0\\ 0& f& 0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=\left[\begin{array}{cccc}{f}_x& 0& u_0& 0\\ 0& f_y& v_0& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right] \\ =K\ast M1\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=M\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]=\left[\begin{array}{cccc}{m}_{11}& m_{12}& m_{13}& m_{14}\\ m_{21}& m_{22}& m_{23}& m_{24}\\ m_{31}& m_{32}& m_{33}& m_{34}\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right] \end{gathered}$$
其中，
$$\begin{gathered} f_x=\frac{f}{dx} \\ {f}_y=\frac{f}{dy} \\ K=\left[\begin{array}{cccc}{f}_x& 0& 0& 0\\ 0& f_y& 0& 0\\ 0& 0& 1& 0\end{array}\right] \\ M1=\left[\begin{array}{cc}R& t\\ 0^T& 1\end{array}\right] \end{gathered}$$

$f_x,f_y$分别是图像水平轴和垂直轴的尺度因子。$K$的参数中只包含焦距、主点坐标等，只由相机的内部结构决定，因此称 $K$ 为内部参数矩阵，$f_x,f_y,u_0,v_0$叫做内部参数。$M1$中包含的旋转矩阵和平移向量是由相机坐标系相对于世界坐标系的位置决定的，因此称$M1$为相机的外部参数矩阵，$R$和$t$叫做外部参数，$M$叫投影矩阵。相机标定就是确定相机的内部参数和外部参数。

相机畸变

理想的透视模型是针孔成像模型，物和像会满足相似三角形的关系。但是实际上由于相机光学系统存在加工和装配的误差，透镜就并不能满足物和像成相似三角形的关系，所以相机图像平面上实际所成的像与理想成像之间会存在畸变。畸变属于成像的几何失真，是由于像平面上不同区域对图像的放大率不同形成的画面扭曲变形的现象，这种变形的程度从画面中心至画面边缘依次递增，主要在画面边缘反映比较明显。为了减小畸变，拍摄图片时应尽量避免用镜头焦距的最广角端或最远端拍摄。

畸变概述

总之，引起畸变的两个主要因素：
1、透镜形状：径向畸变
2、透镜与成像平面不平行：切向畸变
径向畸变如下图：

切向畸变如下图：

对于象平面中的点，其畸变可由下图说明。
dr:径向畸变
dt:切向畸变

径向畸变：
$$\begin{gathered} x_{corrected}^{\prime }=x^{\prime }(1+k_1{r}^2+k_2{r}^4+k_3{r}^6) \\ {y}_{corrected}^{\prime }=y^{\prime }(1+k_1{r}^2+k_2{r}^4+k_3{r}^6) \end{gathered}$$
切向畸变：
$$\begin{gathered} x_{corrected}^{\prime }=x+2p_{1}xy+p_2(r^2+2x^2) \\ {y}_{corrected}^{\prime }=y+p_1(x^2+2y^2)+2p_{2}xy \end{gathered}$$

畸变详细推导

其中$m_r(x_r,y_r)$表示实际投影点的像平面坐标系下的物理坐标，$m_i(x_i,y_i)$表示理想投影点的像平面坐标系下的物理坐标。镜头的畸变模型可表示为：
$$\{\begin{array}{l}{x}_i=x_r+{\sigma }_x\\ \\ y_i=y_r+{\sigma }_y\end{array}$$
${\sigma }_x$和${\sigma }_y$是非线性畸变值，它包括径向畸变，偏心畸变和薄棱镜畸变等。

理论上来说镜头都存在径向和切向畸变，但是通常径向畸变较大，切向畸变较小。径向畸变的模型可由下面的模型来表示：
$$\{\begin{array}{l}{\sigma }_x=x_r(k_1{r}^2+k_2{r}^4+\cdot \cdot \cdot )\\ \\ {\sigma }_y=y_r(k_1{r}^2+k_2{r}^4+\cdot \cdot \cdot )\end{array}$$
其中，$k_1,k_2,k_3\cdot \cdot \cdot$表示径向畸变系数，$r=\sqrt{x_r^2+y_r^2}$；通常情况下径向畸变系数只考虑到一阶或二阶就可以满足精度需求了。

偏心畸变模型是由于多个光学镜头的光轴不能完全共线产生的，这种畸变是由径向和切向畸变共同构成的，数学模型可表示如下：
$$\{\begin{array}{l}{\sigma }_x=p_1{x}_r(3x_r^2+y_r^2)+2p_2{x}_r{y}_r+o[(x_r,y_r{)}^4]\\ \\ {\sigma }_y=p_2{x}_r(3x_r^2+y_r^2)+2p_1{x}_r{y}_r+o[(x_r,y_r{)}^4]\end{array}$$
其中$p_1,p_2$为切向畸变系数。
薄棱镜畸变是由于镜头设计制造缺陷和加工安装所造成的，如镜头与相机成像平面有一个很小的倾角等。因为薄棱镜畸变非常小，通常不考虑，这里只考虑径向畸变和偏心畸变，总的可以表示为：
$$\{\begin{array}{l}{x}_i=x_r+x_r(k_1{r}^2+k_2{r}^4)+p_1{x}_r(3x_r^2+y_r^2)+2p_2{x}_r{y}_r\\ \\ y_i=y_r+y_r(k_1{r}^2+k_2{r}^4)+p_2{x}_r(3x_r^2+y_r^2)+2p_1{x}_r{y}_r\end{array}$$
实际的成像模型为：
$$\{\begin{array}{l}u=f_x(x_r+x_r(k_1{r}^2+k_2{r}^4)+p_1{x}_r(3x_r^2+y_r^2)+2p_2{x}_r{y}_r)+u_0\\ \\ v=f_y(y_r+y_r(k_1{r}^2+k_2{r}^4)+p_2{x}_r(3x_r^2+y_r^2)+2p_1{x}_r{y}_r)+v_0\end{array}$$

双目相机模型

针孔相机模型描述了单个相机的成像模型。然而,仅根据一个像素,我们是无法确定这个空间点的具体位置的。这是因为,从相机光心到归一化平面连线上的所有点,都可以投影至该像素上。只有当 $P$ 的深度确定时(比如通过双目或 RGBD 相机),我们才能确切地知道它的空间位置。

测量像素距离(或深度)的方式有很多种,像人眼就可以根据左右眼看到的景物差异(或称视差)来判断物体与我们的距离。双目相机的原理亦是如此。通过同步采集左右相机的图像,计算图像间视差,来估计每一个像素的深度。双目相机一般由左眼和右眼两个水平放置的相机组成。当然也可以做成上下两个目,但我们见到的主流双目都是做成左右的。在左右双目的相机中,我们可以把两个相机都看作针孔相机。它们是水平放置的,意味两个相机的光圈中心都位于 x 轴上。它们的距离称为双目相机的基线(Baseline, 记作 $b$),是双目的重要参数。

现在,考虑一个空间点 $P$ ,它在左眼和右眼各成一像,记作$P_L$, $P_R$。由于相机基线的存在,这两个成像位置是不同的。理想情况下,由于左右相机只有在 $x$ 轴上有位移,因此 $P$ 的像也只在 $x$ 上有差异。我们记它在左侧的坐标为 $u_L$ ,右侧坐标为 $u_R$ 。
$$\frac{z-f}{z}=\frac{b-u_L+u_R}{b}$$

稍加整理,得：
$$z=\frac{fb}{d},d=u_L-u_R$$

这里 $d$ 为左右图的横坐标之差,称为视差(Disparity)。根据视差,我们可以估计一个像素离相机的距离。视差与距离成反比:视差越大,距离越近 ­ 。同时,由于视差最小为一个像素,于是双目的深度存在一个理论上的最大值,由$fb$确定。我们看到,当基线越长时,双目最大能测到的距离就会变远;反之,小型双目器件则只能测量很近的距离。