3.扩散模型探索：DDIM 笔记与思考

DIFFUSION系列笔记|DDIM 数学、思考与 ppdiffuser 代码探索

论文：DENOISING DIFFUSION IMPLICIT MODELS

该 notebook 主要对 DDIM 论文中的公式进行小白推导，同时笔者将使用 ppdiffusers 中的 DDIM 与 DDPM 探索两者之间的联系。读者能够对论文中的大部分公式如何得来，用在了什么地方有初
步的了解。

提示：由于 DDIM 主要基于 DDPM 提出，因此本文章将省略部分 DDPM 中介绍过的基础内容，包括基于马尔科夫链的 Forward Process, Reverse Porcess 及扩散模型训练目标等相关知识。建议读者可以参考 扩散模型探索：DDPM 笔记与思考 或者其他相关文章，初步了解 DDPM 后再继续阅读本文。

V100 16G 配置运行过程中可能出现 Kernel 问题，请尝试使用 V100 32G 配置。

本文将包括以下部分：

1. 总结 DDIM。
2. Non-Markovian Forward Processes： 从 DDPM 出发，记录论文中公式推导
3. 探索与思考：
   • 验证当 $\eta =1$ DDIMScheduler 的结果与 DDPMScheduler 基本相同。
   • DDIM 的加速采样过程
   • DDIM 采样的确定性
   • INTERPOLATION IN DETERMINISTIC GENERATIVE PROCESSES

DDIM 总览

• 不同于 DDPM 基于马尔可夫的 Forward Process，DDIM 提出了 NON-MARKOVIAN FForward Processes。（见 Forward Process）
• 基于这一假设，DDIM 推导出了相比于 DDPM 更快的采样过程。（见探索与思考）
• 相比于 DDPM，DDIM 的采样是确定的，即给定了同样的初始噪声 $x_t$，DDIM 能够生成相同的结果 $x_0$。（见探索与思考）
• DDIM和DDPM的训练方法相同，因此在 DDPM 基础上加上 DDIM 采样方案即可。（见探索与思考）

Forward process

DDIM 论文中公式的符号与 DDPM 不相同，如 DDIM 论文中的 $\alpha$ 相当于 DDPM 中的 $\bar{\alpha }$，而 DDPM 中的 ${\alpha }_t$ 则在 DDIM 中记成 $\frac{{\alpha }_t}{{\alpha }_{t-1}}$ ，但是运算思路一致，如DDIM 论文中的公式 $(1)-(5)$ 都在 DDPM 中能找到对应公式。

以下我们统一采用 DDPM 中的符号进行标记。即 ${\bar{\alpha }}_t={\alpha }_1{\alpha }_2...{\alpha }_t$

在 DDPM 笔记 扩散模型探索：DDPM 笔记与思考 中，我们总结了 DDPM 的采样公式推导过程为：


$$x_t\stackrel{model}{}{ϵ}_{\theta }(x_t,t)\stackrel{P(x_t|x_0)\to P(x_0|x_t,{ϵ}_{\theta })}{}{\hat{x}}_0(x_t,{ϵ}_{\theta })\stackrel{推导}{}\mu (x_t,{\hat{x}}_0),{\beta }_t\stackrel{P(x_{t-1}|x_t,x_0)}{}{\hat{x}}_{t-1}$$

而后我们用 ${\hat{x}}_{t-1}$ 来近似 $x_{t-1}$，从而一步步实现采样的过程。不难发现 DDPM 采样和优化损失函数过程中，并没有使用到 $p(x_{t-1}|x_t)$ 的信息。因此 DDIM 从一个更大的角度，大胆地将 Forward Process 方式更换了以下式子（对应 DDIM 论文公式 $(7)$）：

$$q_{\sigma }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0\right)=\mathcal{N}\left({\mathbf{x}}_{t-1};\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}\frac{{\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0}{\sqrt{1-{\bar{\alpha }}_t}},{\sigma }_t^2\mathbf{I}\right)\text{\hspace{1em}(1)}$$

论文作者提到了 $(1)$ 式这样的 non-Markovian Forward Process 满足 :

$$q(x_t|x_0)=N(x_t;\sqrt{{\bar{\alpha }}_t}{x}_0,(1-{\bar{\alpha }}_t)I),{\bar{\alpha }}_t=\prod _T{\alpha }_t\text{\hspace{1em}(2)}$$

公式 $(1)$ 能够通过贝叶斯公式：

$$q(x_t|x_{t-1},x_0)=\frac{q(x_{t-1}|x_t,x_0)q(x_t|x_0)}{q(x_{t-1}|x_0)}\text{\hspace{1em}(3)}$$

推导得来。至于如何推导，生成扩散模型漫谈（四）：DDIM = 高观点DDPM 中通过待定系数法给出了详细的解释，由于解释计算过程较长，此处就不展开介绍了。

根据 $(1)$，将 DDPM 中得到的公式（同 DDIM 论文中的公式 $(9)$）：

$$x_0=\frac{{\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}{\sqrt{{\bar{\alpha }}_t}}\text{\hspace{1em}(4)}$$

带入，我们能写出采样公式（即论文中的核心公式 $(12)$）：

$${\mathbf{x}}_{t-1}=\sqrt{{\bar{\alpha }}_{t-1}}\underset{\text{" predicted }{\mathbf{x}}_0\text{ " }}{\left(\frac{{\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}{\sqrt{{\bar{\alpha }}_t}}\right)}+\underset{\text{"direction pointing to }{\mathbf{x}}_t\text{ " }}{\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}\cdot {ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}+\underset{\text{random noise }}{{\sigma }_t{ϵ}_t}\text{\hspace{1em}(5)}$$

其中，$\sigma$ 可以参考 DDIM 论文的核心公式 $(16)$ ：

$${\sigma }_t=\eta \sqrt{(1-{\bar{\alpha }}_{t-1})/(1-{\bar{\alpha }}_t)}\sqrt{1-{\bar{\alpha }}_t/{\bar{\alpha }}_{t-1}}\text{\hspace{1em}(6)}$$

如果 $\eta =0$，那么生成过程就是确定的，这种情况下为 DDIM。

论文中指出，当 $\eta =1$ ，该 forward process 变成了马尔科夫链，该生成过程等价于 DDPM 的生成过程。也就是说当 $\eta =1$ 时，公式 $(5)$ 等于 DDPM 的采样公式，即公式 $(7)$ ：

$$\begin{array}{rl}{\hat{x}}_{t-1}& =\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))+{\sigma }_{t}z\\ & \text{where }z=N(0,I)\end{array}\text{\hspace{1em}(7)}$$

将 $(6)$ 式带入到 $(1)$ 式中得到 DDPM 分布公式（本文章标记依照 DDPM 论文，因此有 ${\bar{\alpha }}_t={\prod }_T{\alpha }_t$）：

$$\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}=\frac{1-{\bar{\alpha }}_{t-1}}{\sqrt{1-{\bar{\alpha }}_t}}\sqrt{{\alpha }_t}\text{\hspace{1em}(8)}$$

···

$$\begin{array}{rl}\frac{\sqrt{1-{\bar{\alpha }}_t}}{\sqrt{1-{\bar{\alpha }}_t}}\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}& =\frac{\sqrt{[(1-{\bar{\alpha }}_{t-1}-(\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t})(1-{\alpha }_t)](1-{\bar{\alpha }}_t)}}{\sqrt{1-{\bar{\alpha }}_t}}\\ & =\frac{\sqrt{(1-{\bar{\alpha }}_{t-1})(1-(\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t})(1-{\alpha }_t))(1-{\bar{\alpha }}_{t-1})}}{\sqrt{1-{\bar{\alpha }}_t}}\\ & =\frac{\sqrt{(1-{\bar{\alpha }}_{t-1})(1-{\bar{\alpha }}_t-1+\frac{{\bar{\alpha }}_t}{{\bar{\alpha }}_{t-1}})}}{\sqrt{1-{\bar{\alpha }}_t}}\\ & =\frac{\sqrt{(1-{\bar{\alpha }}_{t-1})(1-{\bar{\alpha }}_{t-1})\frac{{\bar{\alpha }}_t}{{\bar{\alpha }}_{t-1}}}}{\sqrt{1-{\bar{\alpha }}_t}}\\ & =\frac{1-{\bar{\alpha }}_{t-1}}{\sqrt{1-{\bar{\alpha }}_t}}\sqrt{{\alpha }_t}\end{array}$$

带入得到：

$$\begin{array}{rl}{\mathbf{x}}_{t-1}& =\sqrt{{\bar{\alpha }}_{t-1}}\underset{\text{" predicted }{\mathbf{x}}_0\text{ " }}{\left(\frac{{\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}{\sqrt{{\bar{\alpha }}_t}}\right)}+\underset{\text{"direction pointing to }{\mathbf{x}}_t\text{ " }}{\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}\cdot {ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}+\underset{\text{random noise }}{{\sigma }_t{ϵ}_t}\\ & =\frac{1}{{\sqrt{\alpha }}_t}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }^{(t)}\right)+{\sigma }_t{ϵ}_t\end{array}\text{\hspace{1em}(9)}$$

···

$$\begin{array}{rl}{\mathbf{x}}_{t-1}& =\sqrt{{\bar{\alpha }}_{t-1}}\underset{\text{" predicted }{\mathbf{x}}_0\text{ " }}{\left(\frac{{\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}{\sqrt{{\bar{\alpha }}_t}}\right)}+\underset{\text{"direction pointing to }{\mathbf{x}}_t\text{ " }}{\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}\cdot {ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}+\underset{\text{random noise }}{{\sigma }_t{ϵ}_t}\\ & =\sqrt{\frac{{\bar{\alpha }}_{t-1}}{{\bar{\alpha }}_t}}{x}_t-\sqrt{\frac{{\bar{\alpha }}_{t-1}}{{\bar{\alpha }}_t}}\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }^{(t)}+\frac{1-{\bar{\alpha }}_{t-1}}{\sqrt{1-{\bar{\alpha }}_t}}\sqrt{{\alpha }_t}{ϵ}_{\theta }^{(t)}+{\sigma }_t{ϵ}_t\\ & =\frac{1}{{\sqrt{\alpha }}_t}{x}_t-\frac{1}{{\sqrt{\alpha }}_t\sqrt{1-{\bar{\alpha }}_t}}\left(1-{\bar{\alpha }}_t+(1-{\bar{\alpha }}_{t-1}){\alpha }_t\right){ϵ}_{\theta }^{(t)}+{\sigma }_t{ϵ}_t\\ & =\frac{1}{{\sqrt{\alpha }}_t}\left(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }^{(t)}\right)+{\sigma }_t{ϵ}_t\\ & =\frac{1}{{\sqrt{\alpha }}_t}\left(x_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }^{(t)}\right)+{\sigma }_t{ϵ}_t\end{array}$$

因此，根据推导，$\eta =1$ 时候的 Forward Processes 等价于 DDPM，我们将在 notebook 后半部分，通过代码的方式验证当 $\eta =1$ DDIM 的结果与 DDPM 基本相同。

探索与思考

接下来将根据 ppdiffusers，探索以下四个内容：

1. 验证当 $\eta =1$ DDIM 论文提出的的采样方式结果与 DDPM 基本相同。
2. DDIM 的加速采样过程
3. DDIM 采样的确定性
4. INTERPOLATION IN DETERMINISTIC GENERATIVE PROCESSES

为了支持调参与打印输出，笔者对 ppdifusers 源码进行了微小的更改，各模型的计算思路与架构不变。详细可以参考 notebook 下的 ppdiffusers 文件夹

配置环境

!pip install -q -r ppdiffusers/requirements.txt

import sys
sys.path.append("ppdiffusers")
# sys.path.append("ppdiffusers/ppdiffusers")

import paddle
import numpy as np

from ppdiffusers import DDPMPipeline, DDPMScheduler, DDIMScheduler

from notebook_utils import *

DDIM 与 DDPM 探索

验证当 $\eta =1$ DDIM 的结果与 DDPM 基本相同。

我们使用 google/ddpm-celebahq-256 人像模型权重进行测试，根据上文的推导，当 $\eta =1$ 时，我们期望 DDIM 论文中的 Forward Process 能够得出与 DDPM 相同的采样结果。由于 DDIM 与 DDPM 训练过程相同，因此我们将使用 DDPMPipeline 加载模型权重 google/ddpm-celebahq-256 ，而后采用 DDIMScheduler() 进行图片采样，并将采样结果与 DDPMPipeline 原始输出对比。
如下：

# DDPM 生成图片
pipe = DDPMPipeline.from_pretrained("google/ddpm-celebahq-256")

paddle.seed(33)
ddpm_output = pipe()  # 原始 ddpm 输出

# 我们采用 DDPM 的训练结果，通过 DDIM Scheduler 来进行采样。
pipe.scheduler = DDIMScheduler()

# 设置与 DDPM 相同的采样结果，令 DDIM 采样过程中的 eta = 1.
paddle.seed(33)
ddim_output = pipe(num_inference_steps=1000, eta=1)

imgs = [ddpm_output.images[0], ddim_output.images[0]]
titles = ["ddpm", "ddim"]
compare_imgs(imgs, titles)  # 该函数在 notebook_utils.py 声明

[2022-12-25 17:33:13,215] [    INFO] - Downloading model_index.json from https://bj.bcebos.com/paddlenlp/models/community/google/ddpm-celebahq-256/model_index.json
100%|██████████| 186/186 [00:00<00:00, 176kB/s]
[2022-12-25 17:33:13,323] [    INFO] - Downloading model_state.pdparams from https://bj.bcebos.com/paddlenlp/models/community/google/ddpm-celebahq-256/unet/model_state.pdparams
100%|██████████| 434M/434M [00:15<00:00, 28.5MB/s] 
[2022-12-25 17:33:29,461] [    INFO] - Downloading config.json from https://bj.bcebos.com/paddlenlp/models/community/google/ddpm-celebahq-256/unet/config.json
100%|██████████| 792/792 [00:00<00:00, 457kB/s]
W1225 17:33:29.589558  1052 gpu_resources.cc:61] Please NOTE: device: 0, GPU Compute Capability: 7.0, Driver API Version: 11.2, Runtime API Version: 11.2
W1225 17:33:29.594818  1052 gpu_resources.cc:91] device: 0, cuDNN Version: 8.2.
[2022-12-25 17:33:32,970] [    INFO] - Downloading scheduler_config.json from https://bj.bcebos.com/paddlenlp/models/community/google/ddpm-celebahq-256/scheduler/scheduler_config.json
100%|██████████| 258/258 [00:00<00:00, 249kB/s]



  0%|          | 0/1000 [00:00

通过运行以上代码，我们可以看出 $\eta =1$ 时， 默认配置下 DDPM 与 DDIM 采样结果有着明显的区别。但这并不意味着论文中的推导结论是错误的，差异可能源于以下两点：

1. 计算机浮点数精度问题
2. Scheduler 采样过程中存在的 clip 操作导致偏差。

计算机浮点数精度问题

我们可以进行以下操作：分别调用 DDIM 与 DDPM scheduler 的 ._get_variance() 操作。在两个采样器配置相同的情况下，得到的方差应该也相同才对。

# 获得 DDPM, DDIM 采样器
ddpmscheduler = DDPMScheduler()
ddimscheduler= DDIMScheduler()
ddimscheduler.set_timesteps(1000)
ddpmscheduler.set_timesteps(1000)

print("ddim get variance for step 999", ddimscheduler._get_variance(999,998))
print("ddpm get variance for step 999", ddpmscheduler._get_variance(999))

ddim get variance for step 999 Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0.01999996])
ddpm get variance for step 999 Tensor(shape=[1], dtype=float32, place=Place(gpu:0), stop_gradient=True,
       [0.01999998])

以上代码中，两个采样器同一时间步下的方差有些许不同，大致原因是计算机浮点精度问题，如：

beta = 0.02
alpha = 1-beta
print(1-alpha == beta)  # False

如果要做到方差完全相同，那么只需要在 ppdiffusers.ppdiffusers.schedulers.scheduling_ddpm 200 行换为以下代码即可。

variance = (1 - alpha_prod_t_prev) / (1 - alpha_prod_t) * (1-self.alphas[t])

但经过实验对比，更改方差计算方式后，采样结果没有太多变化。

尝试去除 Clip 操作

Scheduler 采样过程中存在的 clip 操作导致偏差。Clip 操作对采样过程中生成的 x_0 预测结果进行了截断，尽管 DDPM, DDIM 均在预测完 $x_0$ 后进行了截断，但根据上文的推导公式，两者采样过程中 $x_0$ 权重的不同，可能导致了使用 clip 时，两者的采样结果有着明显区别。

将 clip 配置设置成 False 后， DDPM 与 DDIM($\eta =1$) 的采样结果基本上相同了。如以下代码，我们尝试测试去除 clip 配置后的采样结果：

pipe = DDPMPipeline.from_pretrained("google/ddpm-celebahq-256")
pipe.progress_bar = lambda x:x  # uncomment to see progress bar

# 我们采用 DDPM 的训练结果，通过 DDIM Scheduler 来进行采样。
# print("Default setting for DDPM:\t",pipe.scheduler.config.clip_sample)  # True
pipe.scheduler.config.clip_sample = False
paddle.seed(33)
ddpm_output = pipe()

pipe.scheduler = DDIMScheduler()
# print("Default setting for DDIM:\t",pipe.scheduler.config.clip_sample)  # True
pipe.scheduler.config.clip_sample = False
paddle.seed(33)
ddim_output = pipe(num_inference_steps=1000, eta=1)

imgs = [ddpm_output.images[0], ddim_output.images[0]]
titles = ["DDPM no clip", "DDIM no clip"]
compare_imgs(imgs, titles)

[2022-12-25 17:35:29,510] [    INFO] - Already cached /home/aistudio/.paddlenlp/models/google/ddpm-celebahq-256/model_index.json
[2022-12-25 17:35:29,513] [    INFO] - Already cached /home/aistudio/.paddlenlp/models/google/ddpm-celebahq-256/unet/model_state.pdparams
[2022-12-25 17:35:29,515] [    INFO] - Already cached /home/aistudio/.paddlenlp/models/google/ddpm-celebahq-256/unet/config.json
[2022-12-25 17:35:30,794] [    INFO] - Already cached /home/aistudio/.paddlenlp/models/google/ddpm-celebahq-256/scheduler/scheduler_config.json

duler_config.json

DDIM 加速采样

论文附录 C 有对这一部分进行详细阐述。DDIM 优化时与 DDPM 一样，对噪声进行拟合，但 DDIM 提出了通过一个更短的 Forward Processes 过程，通过减少采样的步数，来加快采样速度：

从原先的采样序列 $\{1,...,T\}$ 中选择一个子序列来生成图像。如原序列为 1 到 1000，抽取子序列可以是 1, 100, 200, … 1000 （类似 arange(1, 1000, 100)）。抽取方式不固定。在生成时同样采用公式 $(1)$，其中的 timestep $t$ ，替换为子序列中的 timestep。其中的 ${\bar{\alpha }}_t$ 对应到训练时候的数值，比如采样 1, 100, 200, ... 1000 中的第二个样本，则使用训练时候采用的 ${\bar{\alpha }}_{100}$ （此处只能替换 alphas_cumprod $\bar{\alpha }$，不能直接替换 alpha 参数 ${\alpha }_t$）。

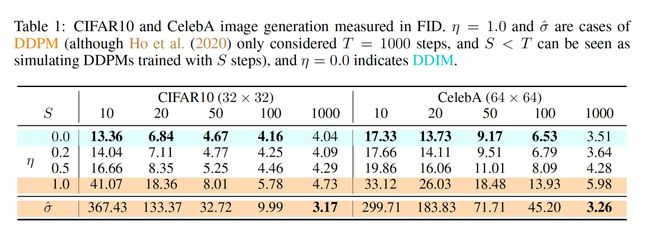
参考论文中的 Figure 3，在加速生成的情况下，$\eta$ 越小，生成的图片效果越好，同时 $\eta$ 的减小能够很大程度上弥补采样步数减少带来的生成质量下降问题。

pipe.progress_bar = lambda x:x  # cancel process bar
etas = [0, 0.4, 0.8]
steps = [10, 50, 100, 1000]
fig = plt.figure(figsize=(7, 7))
for i in range(len(etas)):
    for j in range(len(steps)):
        plt.subplot(len(etas), len(steps), j+i*len(steps) + 1)
        paddle.seed(77)
        sample1 = pipe(num_inference_steps=steps[j], eta=etas[i])
        plt.imshow(sample1.images[0])
        plt.axis("off")
        plt.title(f"eta {etas[i]}|step {steps[j]}")
plt.show()

通过以上可以发现几点：

• $\eta$ 越小，采样步数产生的图片质量和风格差异就越小。
• $\eta$ 的减小能够很大程度上弥补采样步数减少带来的生成质量下降问题。

DDIM 采样的确定性

由于 DDIM 在生成过程中 $\eta =0$，因此采样过程中不涉及任何随机因素，最终生成图片将由一开始输入的图片噪声 $x_t$ 决定。

paddle.seed(77)
x_t = paddle.randn((1, 3, 256, 256))
paddle.seed(8)
sample1 = pipe(num_inference_steps=50,eta=0,x_t=x_t)
paddle.seed(9)
sample2 = pipe(num_inference_steps=50,eta=0,x_t=x_t)
compare_imgs([sample1.images[0], sample2.images[0]], ["sample(seed 8)", "sample(seed 9)"])

图像重建

在 DDIM 论文中，其作者提出了可以将一张原始图片 $x_0$ 经过足够长的步数 $T$ 加噪为 $x_T$，而后通过 ODE 推导出来的采样方式，尽可能的还原原始图片。
根据公式 $(5)$（即论文中的公式 12），我们能够推理得到论文中的公式 $(13)$:

$$\frac{{\mathbf{x}}_{t-\Delta t}}{\sqrt{{\alpha }_{t-\Delta t}}}=\frac{{\mathbf{x}}_t}{\sqrt{{\alpha }_t}}+\left(\sqrt{\frac{1-{\alpha }_{t-\Delta t}}{{\alpha }_{t-\Delta t}}}-\sqrt{\frac{1-{\alpha }_t}{{\alpha }_t}}\right){ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)\text{\hspace{1em}(10)}$$

···

$$\begin{array}{rl}{\mathbf{x}}_{t-1}& =\sqrt{{\bar{\alpha }}_{t-1}}\underset{\text{" predicted }{\mathbf{x}}_0\text{ " }}{\left(\frac{{\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}{\sqrt{{\bar{\alpha }}_t}}\right)}+\underset{\text{"direction pointing to }{\mathbf{x}}_t\text{ " }}{\sqrt{1-{\bar{\alpha }}_{t-1}-{\sigma }_t^2}\cdot {ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}+\underset{\text{random noise }}{{\sigma }_t{ϵ}_t}\\ \frac{x_{t-1}}{\sqrt{{\bar{\alpha }}_{t-1}}}& =\frac{x_t}{\sqrt{{\bar{\alpha }}_t}}-\frac{\sqrt{1-{\bar{\alpha }}_t}}{\sqrt{{\bar{\alpha }}_t}}{ϵ}_{\theta }^{(t)}+\frac{\sqrt{1-{\bar{\alpha }}_{t-1}}}{\sqrt{{\bar{\alpha }}_{t-1}}}{ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)\\ & \text{当 t 足够大时可以看做}\\ \frac{{\mathbf{x}}_{t-\Delta t}}{\sqrt{{\bar{\alpha }}_{t-\Delta t}}}& =\frac{x_t}{\sqrt{{\bar{\alpha }}_t}}+\left(\sqrt{\frac{1-{\bar{\alpha }}_{t-\Delta t}}{{\bar{\alpha }}_{t-\Delta t}}}-\sqrt{\frac{1-{\bar{\alpha }}_t}{{\bar{\alpha }}_t}}\right){ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)\end{array}$$

而后进行换元，令 $\sigma =(\sqrt{1-\bar{\alpha }}/\sqrt{\bar{\alpha }}),\bar{x}=x/\sqrt{\bar{\alpha }}$，带入得到：

$$\mathrm{d}\overline{\mathbf{x}}(t)={ϵ}_{\theta }^{(t)}\left(\frac{\overline{\mathbf{x}}(t)}{\sqrt{{\sigma }^2+1}}\right)\mathrm{d}\sigma (t)\text{\hspace{1em}(11)}$$

于是，基于这个 ODE 结果，能通过 $\bar{x}(t)+d\bar{x}(t)$ 计算得到 $\bar{x}(t+1)$ 与 $x_{t+1}$

根据 github - openai/improved-diffusion，其实现根据 ODE 反向采样的方式为：直接根据公式 $(5)$ 进行变换，把 $t-1$ 换成 $t+1$：

$${\mathbf{x}}_{t+1}=\sqrt{{\bar{\alpha }}_{t+1}}\underset{\text{" predicted }{\mathbf{x}}_0\text{ " }}{\left(\frac{{\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}{\sqrt{{\bar{\alpha }}_t}}\right)}+\underset{\text{"direction pointing to }{\mathbf{x}}_t\text{ " }}{\sqrt{1-{\bar{\alpha }}_{t+1}}\cdot {ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)}+\underset{\text{random noise }}{{\sigma }_t{ϵ}_t}\text{\hspace{1em}(12)}$$

而参考公式 $(11)$ 的推导过程，$(12)$ 可以看成下面这种形式：

$$\frac{{\mathbf{x}}_{t+\Delta t}}{\sqrt{{\bar{\alpha }}_{t+\Delta t}}}=\frac{x_t}{\sqrt{{\bar{\alpha }}_t}}+\left(\sqrt{\frac{1-{\bar{\alpha }}_{t+\Delta t}}{{\bar{\alpha }}_{t+\Delta t}}}-\sqrt{\frac{1-{\bar{\alpha }}_t}{{\bar{\alpha }}_t}}\right){ϵ}_{\theta }^{(t)}\left({\mathbf{x}}_t\right)\text{\hspace{1em}(13)}$$

以下我们尝试对自定义的输入图片进行反向采样（reverse sampling）和原图恢复，我们导入本地图片：

from PIL import Image
# 查看原始图片
raw_image = Image.open("imgs/sample2.png").crop((0,0,350,350)).resize((256,256))
raw_image.show()

ppdiffusers 中不存在 reverse_sample 方案，因此我们根据本文中的公式 $(12)$ 来实现一下 reverse_sample 过程，具体为：

    def reverse_sample(self, model_output, x, t, prev_timestep):
        """
        Sample x_{t+1} from the model and x_t using DDIM reverse ODE.
        """

        alpha_bar_t_next = self.alphas_cumprod[t]
        alpha_bar_t = self.alphas_cumprod[prev_timestep] if prev_timestep >= 0 else self.final_alpha_cumprod

        inter = (
                        ((1-alpha_bar_t_next)/alpha_bar_t_next)** (0.5)- \
                        ((1-alpha_bar_t)/alpha_bar_t)** (0.5)
                    )
        x_t_next = alpha_bar_t_next** (0.5) * (x/ (alpha_bar_t ** (0.5)) + \
                    (
                    model_output * inter
                    )
                )

        return x_t_next

为了方便 alpha 等参数的调用，笔者将该方法整理到了 ppdiffusers/ppdiffusers/schedulers/scheduling_ddim.py/DDIMScheduer 中。

# 进行反向采样与解码
T = 200

def add_noise_by_reverse_sample(pipe, raw_image, T):
    """
    receive a raw image, convert to $x_0$ and construct $x_{t}$ using reverse sample.
    """
    image = paddle.to_tensor([np.array(raw_image)])
    image = (image/127.5 - 1).transpose([0,3,1,2])
    pipe.scheduler.set_timesteps(T)
    with paddle.no_grad():
        for t in pipe.progress_bar(pipe.scheduler.timesteps[::-1]):
            prev_timestep = t - pipe.scheduler.config.num_train_timesteps // pipe.scheduler.num_inference_steps
            model_output=pipe.unet(image, prev_timestep).sample
            image = pipe.scheduler.reverse_sample(model_output=model_output,
                                                  x=image,
                                                  t=t,
                                                  prev_timestep=prev_timestep)
    image2show = (image / 2 + 0.5).clip(0, 1).transpose([0, 2, 3, 1]).cast("float32").numpy()
    image2show = pipe.numpy_to_pil(image2show)
    return image, image2show
pipe.scheduler.config.clip_sample = False  # 同上述实验，我们必须关掉 clip

image, image2show = add_noise_by_reverse_sample(pipe, raw_image, T)
sample1 = pipe(num_inference_steps=T,eta=0,x_t=image)

# see what image look like
compare_imgs([sample1.images[0],image2show[0]], [f"Reconstructed Image (T={T})",f"Reversed Noise(T={T})"])

T = 100
image, image2show = add_noise_by_reverse_sample(pipe, raw_image, T)
sample1 = pipe(num_inference_steps=T,eta=0,x_t=image)

# see what image look like
compare_imgs([sample1.images[0],image2show[0]], [f"Reconstructed Image (T={T})",f"Reversed Noise(T={T})"])

可以看到，我们通过 ODE 的方式，对图片进行加噪之后，变成右边的电视画面。而在重新采样之后，得到了一张与原图片相似的图片，图片的还原图随着时间布的增大而增加。

潜在的风格融合方式

通过两个能够生成不同图片的噪声 $z_1,z_2$，进行 spherical linear interpolation 球面线性插值。而后作为 $x_T$ 生成具有两张画面共同特点的图片。有点类似风格融合的效果。

paddle.seed(77)
pipe.scheduler.config.clip_sample = False

z_0 = paddle.randn((1, 3, 256, 256))
sample1 = pipe(num_inference_steps=50,eta=0,x_t=z_0)
paddle.seed(2707)
z_1 = paddle.randn((1, 3, 256, 256))
sample2 = pipe(num_inference_steps=50,eta=0,x_t=z_1)
compare_imgs([sample1.images[0], sample2.images[0]], ["sample from z_0", "sample from z_1"])

以上选择 seed 为 77 和 2707 的噪声进行采样，他们的采样结果分别展示在上方。

以下参考 ermongroup/ddim/blob/main/runners/diffusion.py ，对噪声进行插值，方式大致为：

$$\begin{gathered} x_t=\frac{\sin \left((1-\alpha )\theta \right)}{\sin (\theta )}{z}_0+\frac{sin(\alpha \theta )}{\sin (\theta )}{z}_1, \\ where\theta =\arccos \left(\frac{\sum z_1{z}_0}{||z_1|\cdot ||z_0||}\right) \end{gathered}$$

其中 $\alpha$ 用于控制融合的比重，在下面测示例中，$\alpha$ 越大说明 $z_0$ 占比越大。

# Reference: https://github.com/ermongroup/ddim/blob/main/runners/diffusion.py#L296
def slerp(z1, z2, alpha):
    theta = paddle.acos(paddle.sum(z1 * z2) / (paddle.norm(z1) * paddle.norm(z2)))
    return (
        paddle.sin((1 - alpha) * theta) / paddle.sin(theta) * z1
        + paddle.sin(alpha * theta) / paddle.sin(theta) * z2
    )
alphas = [0, 0.2, 0.4, 0.5, 0.6, 0.8, 1]
img_size = 1
fig = plt.figure(figsize=(7, 7))
for i in range(len(alphas)):
    x_t = slerp(z_0, z_1, alphas[i])
    sample_merge = pipe(num_inference_steps=50,eta=0,x_t=x_t)
    plt.subplot(1,len(alphas),1+i)
    plt.imshow(sample_merge.images[0])
    plt.axis("off")

可以看出，当 $\alpha$ 为 0.2， 0.8 时，我们能够看到以下融合的效果，如头发颜色，无关特征等。但在中间部分（$\alpha =0.4,0.5,0.6$），采样的图片质量就没有那么高了。

那根据前两节的阐述，我们可以实现一个小的pipeline， 具备接受使用 DDIM 接受两张图片，而后输出一张两者风格融合之后的图片。

# 查看原始图片
raw_image_1 = Image.open("imgs/sample2.png").crop((20,20,330,330)).resize((256,256))
raw_image_2 = sample1.images[0]

compare_imgs([raw_image_1, raw_image_2], ["image 1", "image 2"])

我们尝试让右边的女士头像具备梅西风格。但是效果看起来很不好的样子。

# 融合两张图片
T = 50
alpha = 0.81  # alpha 参数很重要
z_1, _ = add_noise_by_reverse_sample(pipe, raw_image_1, T)
z_2, _ = add_noise_by_reverse_sample(pipe, sample1.images[0], T)
x_t = slerp(z_1, z_2, alpha)
sample_merge = pipe(num_inference_steps=T,eta=0,x_t=x_t)
compare_imgs([sample1.images[0],sample_merge.images[0] ], ["sample 1", "sample 1 merged messi style"])

总结

以上便是 DDIM 的介绍，在下一份笔记中，笔者将继续探索 ppdiffusers 中开源出来的 diffusion sde 系列模型。

参考

Denoising Diffusion Implicit Models

苏建林 - 生成扩散模型漫谈 系列笔记

小小将 - 扩散模型之DDIM

github - openai/improved-diffusion

请点击此处查看本环境基本用法.

Please click here for more detailed instructions.

此文章为搬运
[原项目链接].(https://aistudio.baidu.com/aistudio/projectdetail/5368825?forkThirdPart=1)