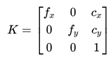orb_slam2坐标系的理解
原因:orb_slam2学习过程中,会遇到许多关于相机pose和图片的转化问题,想要理解他们的原理,需要缕清各种坐标系之间的关系。
介绍:slam中涉及到四个常用坐标系,包括 像素坐标系(u,v)、图像坐标系(x,y)、相机坐标系(Xc,Yc,Zc)和世界坐标系(Xw,Yw,Zw)
1.像素坐标系与图像坐标系
像素坐标系以图像左上角为原点建立以像素为单位的直接坐标系u-v。(在OpenCV中u对应x,v对应y)
图1 图像坐标系
由于(u,v)只代表像素的列数与行数,而像素在图像中的位置并没有用物理单位表示出来,所以,我们还要建立以物理单位(如毫米)表示的图像坐标系x-y。将相机光轴与图像平面的交点(一般位于图像平面的中心处,也称为图像的主点(principal point)定义为该坐标系的原点O1,且x轴与u轴平行,y轴与v轴平行,假设(u0,v0)代表O1在u-v坐标系下的坐标,dx与dy分别表示每个像素在横轴x和纵轴y上的物理尺寸,则图像中的每个像素在u-v坐标系中的坐标和在x-y坐标系中的坐标之间都存在如下的关系:
其中,我们假设物理坐标系中的单位为毫米,那么dx的的单位为:毫米/像素。那么x/dx的单位就是像素了,即和u的单位一样都是像素。为了使用方便,可将上式用矩阵形式表示为:
2.相机坐标系与图像坐标系
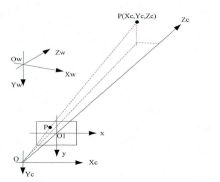
相机成像的几何关系可由图2表示。其中O点为摄像机光心(投影中心),Xc轴和Yc轴与成像平面坐标系的x轴和y轴平行,Zc轴为摄像机的光轴,和图像平面垂直。光轴与图像平面的交点为图像的主点O1,由点O与Xc,Yc,Zc轴组成的直角坐标系称为摄像机的坐标系。OO1为摄像机的焦距。
图2 相机坐标系与世界坐标系,OwXwYwZw即为世界坐标系
相机内参中的fx与fy,计算点在相机坐标系的坐标
当我们用OpenCV相机标定函数去标定相机时,我们能得到一个相机的内部参数,简称“内参”。内参是一个3×3的矩阵,
其中cx和cy可以理解为u0和v0,它们表示相机光轴在图像坐标系中的偏移量,以像素为单位。但对于焦距fx和fy就不是很直观了。其中f是相机的焦距,以像素为单位;d为物体到相机的距离,单位为米;x是物体在图像中的宽度,w为物体的实际宽度;y是物体在图像中的高度,而h是物体的实际高度。而对于一张矩形的图像,则有
fx / d = x / w = 1 / dx => fx = d / dx
fy / d = y / h = 1 / dy => fy = d / dy
三角形相似性:
d / Zc = x / Xc
由 x = ( u - cx ) * dx; => Xc =( u - cx )* dx * Zc / d;
=> Xc = ( u - cx ) * Zc / fx;
=> Yc = ( v - cy ) * Zc / fy;
3.世界坐标系
世界坐标系是为了描述相机的位置而被引入的。平移向量t和旋转矩阵R可以用来表示相机坐标系与世界坐标系的关系。所以,假设空间点P在世界坐标系下的坐标是(Xw,Yw,Zw,1)T,(这里T是上标转置),在相机坐标下的坐标是(Xc,Yc,Zc,1)T,则存在如下的关系:
其中,R是3×3的正交单位矩阵(也成为旋转矩阵),t是三维的平移向量,矢量![]() ,M1是4×4矩阵。
,M1是4×4矩阵。
PS:参考资料
https://baike.baidu.com/item/%E5%83%8F%E7%B4%A0%E5%9D%90%E6%A0%87/5372225?fr=aladdin
https://www.cnblogs.com/zipeilu/p/6658177.html?utm_source=itdadao&utm_medium=referral