第二章.线性回归以及非线性回归—梯度下降法
第二章.线性回归以及非线性回归
2.5 梯度下降法
1.流程:
-
初始化θ0,θ1
-
不断改变θ0,θ1,直到J(θ0,θ1)到达一个全局最小值或局部极小值
2.图像分析:
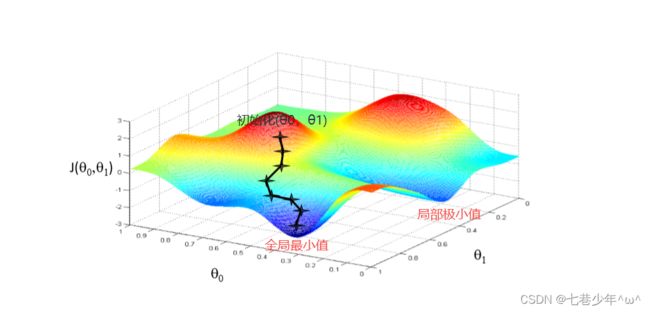
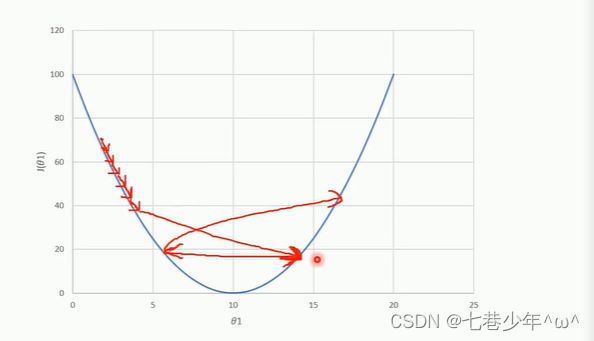
1).图像层面分析代价函数:
①.红色区域表示代价函数的值比较大,蓝色区域表示代价函数的值比较小
②.先给(θ0,θ1)赋一个初始值,然后进行迭代(就是求导,得到一个梯度方向)得到下一个点,不断迭代优化,直到J(θ0,θ1)到达一个全局最小值,最小值所对应的点就是我们所求的值
2).梯度下降法内部循环执行的函数:(当前步到下一步的计算函数)
①.公式

参数说明:
:= :相当于赋值
α:学习率,控制梯度下降法的运动步长(学习率不能太大(有可能一直循环,找不到最小值),也不能太小(耗时长),可以多尝试一些值)
3.梯度下降法的缺点:
初始值(θ0,θ1)的选取位置不同可能会导致J(θ0,θ1)找不到全局最小值,会找到局部最小值。
4.梯度下降法求解线性回归
1).公式:
2).非凸函数和凸函数:
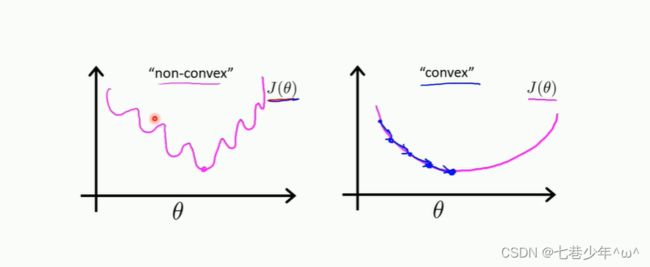
非凸函数:使用梯度下降法可能会存在多个局部极小值,不太适合使用梯度下降法
凸函数:只存在一个全局最小值,比较适合使用梯度下降法
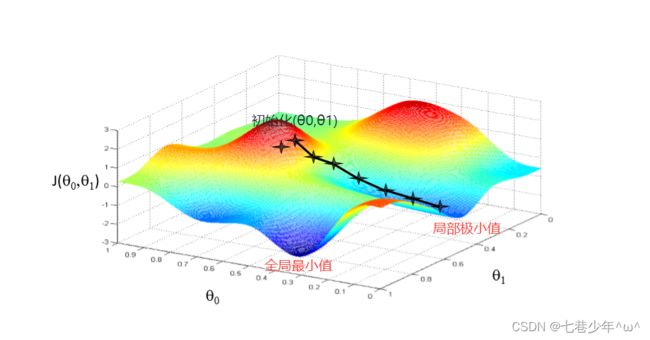
3).线性回归的代价函数是凸函数:
初始值(θ0和θ1)无论怎么选择,使用梯度下降法进行优化都会找到全局最小值,没有局部极小值,线性回归比较适合梯度下降法
5.梯度下降法的优化过程: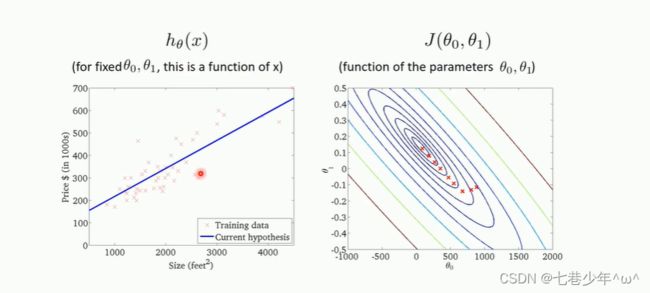
6.实战1: 梯度下降法—一元线性回归:
1).CSV中的数据:
- data.xlsx
- 上传文件为excel文件,需转换成csv文件使用
2).代码
import numpy as np
import matplotlib.pyplot as plt
# 载入数据
data = np.loadtxt('D:\\Data\\data.csv', delimiter=',')
x_data = data[:, 0]
y_data = data[:, 1]
plt.scatter(x_data, y_data)
plt.show()
# 学习率learning rate
lr = 0.0001
# 截距
b = 0
# 斜率
k = 0
# 最大迭代次数
epochs = 50
# 代价函数:最小二乘法
def comuter_error(b, k, x_data, y_data):
totalError = 0
for i in range(0, len(x_data)):
totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
return totalError / float(len(x_data)) / 2.0 # 2除不除都可以,之前的文档有说明
# 梯度下降法
def gradient_descent(x_data, y_data, k, b, lr, epochs):
# 总的数据量
m = float(len(x_data))
for i in range(epochs):
grad_b = 0
grad_k = 0
for j in range(0, len(x_data)):
grad_b += (1 / m) * ((k * x_data[j] + b) - y_data[j])
grad_k += (1 / m) * x_data[j] * ((k * x_data[j] + b) - y_data[j])
# 更新b,k
b = b - lr * grad_b
k = k - lr * grad_k
# #每循环10次输入一次图像
# if i%10==0:
# plt.plot(x_data,y_data,'b.')
# plt.plot(x_data,k * x_data + b,'r')
# plt.show()
return k, b
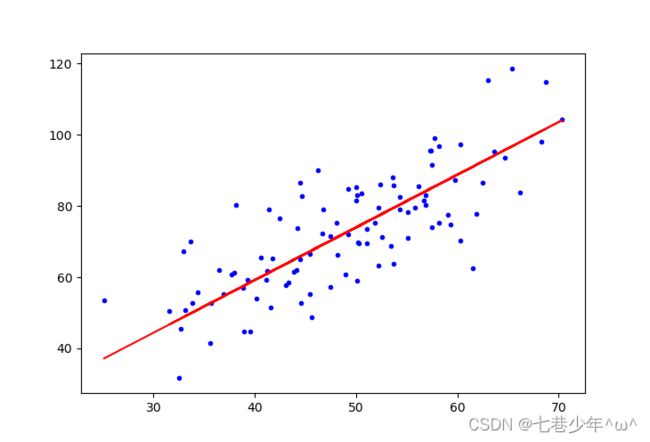
print('初始参数 b={0},k={1},error={2}'.format(b, k, comuter_error(b, k, x_data, y_data)))
k, b = gradient_descent(x_data, y_data, k, b, lr, epochs)
print('结果参数 b={0},k={1},error={2}'.format(b, k, comuter_error(b, k, x_data, y_data)))
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k * x_data + b, 'r')
plt.show()
示:
①.数据
7.实战2: sklearn—一元线性回归:
1).CSV中的数据:
- data.xlsx
- 上传文件为excel文件,需转换成csv文件使用
2).代码
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 载入数据
data = np.loadtxt('D:\\Data\\data.csv', delimiter=',')
x_data = data[:, 0]
y_data = data[:, 1]
plt.scatter(x_data, y_data)
plt.show()
# 维度的变化
x_data = data[:, 0, np.newaxis]
y_data = data[:, 1, np.newaxis]
# 创建并拟合模型
model = LinearRegression(copy_X=True, fit_intercept=True)
model.fit(x_data, y_data)
# 截距
b = model.intercept_
print('截距:', b)
# 回归系数
k = model.coef_
print('回归系数(斜率):', k)
# 画图
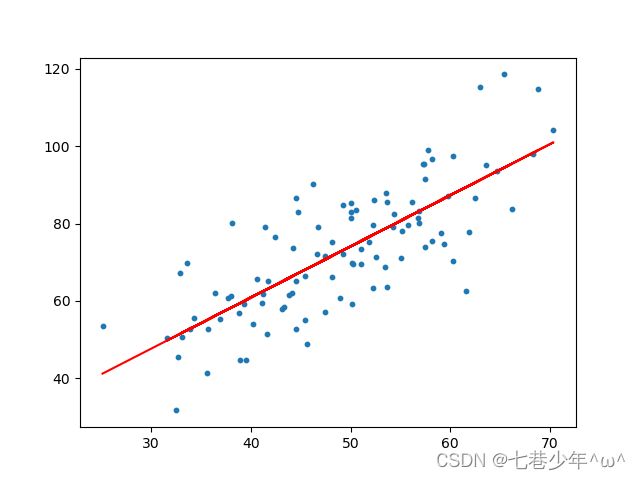
plt.scatter(x_data, y_data, s=10)
plt.plot(x_data, model.predict(x_data), 'r')
plt.show()
3).结果展示:
①.数据