LeetCode数组、字符串
目录
python计算IOU
给定一个数组,求出其中的最大值和次大值。
给定一个数组,求一个k值,使得前k个数的方差 + 后n-k个数的方差最小,时间复杂度可以到O(n)
剑指 Offer 39. 数组中出现次数超过一半的数字
215. 数组中的第K个最大元素
560. 和为K的子数组
未排序数组中累加和为给定值k的最长子数组的长度
0与1个数相等的最长子数组
N数之和系列
15. 三数之和
18. 四数之和
4. 寻找两个正序数组的中位数
162. 寻找峰值
189. 旋转数组
153. 寻找旋转排序数组中的最小值
154. 寻找旋转排序数组中的最小值 II
33. 搜索旋转排序数组
378. 有序矩阵中第 K 小的元素
给定一个只读数组 l,长度是M,最小值是a,最大值是b,l 中的元素两两各不相等。给定内存 O(N) << M, 要求找出 l 的中位数
使用rand5()生成rand7()
41. 缺失的第一个正数
448. 找到所有数组中消失的数字
不同路径
62. 不同路径
63. 不同路径 II
面试题 08.02. 迷路的机器人
64. 最小路径和
174. 地下城游戏
120. 三角形最小路径和
283. 移动零
剑指 Offer 14- I. 剪绳子
300. 最长递增子序列
673. 最长递增子序列的个数
53. 最大子序和
718. 最长重复子数组
循环有序数组中查找某个数
42. 接雨水
322. 零钱兑换
518. 零钱兑换 II
279. 完全平方数
重复元素
287. 寻找重复数
给定一个长度为N的数组,其中每个元素的取值范围都是0到N-1。判断数组中是否有重复的数字。
排列问题
46. 全排列
47. 全排列 II
31. 下一个排列
386. 字典序排数
岛屿问题
200. 岛屿数量
695. 岛屿的最大面积
463. 岛屿的周长
组合总和系列
39. 组合总和
40. 组合总和 II
跳跃系列
55. 跳跃游戏
45. 跳跃游戏 II
跳跃变体
1306. 跳跃游戏 III
股票系列
121. 买卖股票的最佳时机
122. 买卖股票的最佳时机 II
123、买卖股票的最佳时机III
188、买卖股票的最佳时机IV
309、含冷冻期
打家劫舍系列
478. 在圆内随机生成点
179. 最大数
207. 课程表
210. 课程表 II
栈
84. 柱状图中最大的矩形
85. 最大矩形
221. 最大正方形
456. 132 模式
496. 下一个更大元素 I
88. 合并两个有序数组
剑指 Offer 51. 数组中的逆序对
295. 数据流的中位数
483. 最小好进制
字符串
3. 无重复字符的最长子串
76. 最小覆盖子串
面试题 17.18. 最短超串
5. 最长回文子串
647. 回文子串
14. 最长公共前缀
20. 有效的括号
678. 有效的括号字符串
22. 括号生成
32. 最长有效括号
72. 编辑距离
165. 比较版本号
面试题 01.06. 字符串压缩
115. 不同的子序列
28. 实现 strStr()
131. 分割回文串
93. 复原 IP 地址
91. 解码方法
524. 通过删除字母匹配到字典里最长单词
97. 交错字符串
30. 串联所有单词的子串
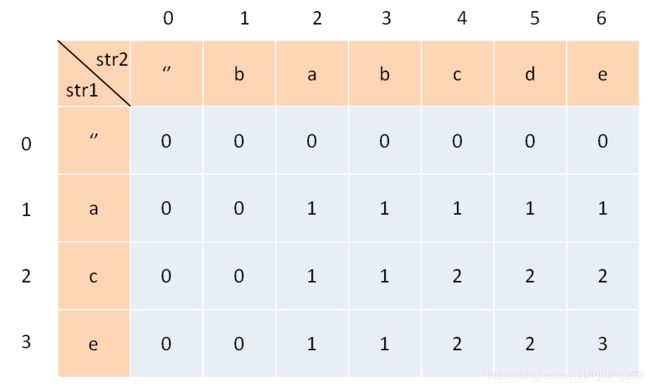
python计算IOU
题意:给定两个box,IOU即交并比
题解:
以(x1, y1)和(x2, y2)分别代表左上角和右下角的坐标。
def iou(box1, box2):
in_h = min(box1[3], box2[3]) - max(box1[1], box2[1])
in_w = min(box1[2], box2[2]) - max(box1[0], box2[0])
if in_h<0 or in_w<0:
inner = 0
else:
inner = in_h*in_w
union=(box1[2]-box1[0])*(box1[3]-box1[1])+(box2[2]-box2[0])*(box2[3]-box2[1])-inner
iou = inner/union
return iou给定一个数组,求出其中的最大值和次大值。
题解:
双指针的思想,交替往后遍历
def getmaxandnext(nums):
max_val = next_val = nums[0]
for num in nums:
if num>max_val:
next_val = max_val
max_val = num
elif num>next_val:
next_val = num
return (max_val, next_val)给定一个数组,求一个k值,使得前k个数的方差 + 后n-k个数的方差最小,时间复杂度可以到O(n)
题解:方差公式为D(X) = E(X^2) - [ E(X)]^2
def minVariance(nums):
s = 0
square_sum = 0
n = len(nums)
left_var = [0]*n
right_var = [0]*n
# 从左到右求每一段的方差
for i in range(n):
s += nums[i]
square_sum += nums[i]*nums[i]
left_var[i] = square_sum/(i+1) - (s/(i+1))**2
s = 0
square_sum = 0
# 从右到左求每一段的方差
for j in range(n-1, -1, -1):
s += nums[j]
square_sum += nums[j]*nums[j]
right_var[j] = square_sum/(n-1) - (s/(i+1))**2
# 两者合并,得到方差最小的两段
index = 0
var = left_var[0] + right_var[0]
for k in range(n-1, -1, -1):
if left_var[k]+right_var[k+1]剑指 Offer 39. 数组中出现次数超过一半的数字
题意: 数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
题解:和169题 多数元素一样,采用“火拼”的方法,即使用count来计数,当当前元素和之前剩下的元素不同时,count-=1,当减少到0时,表示多数元素变成了当前的元素;若当前元素和之前剩下的多数元素相同时,则count+=1 。时间复杂度为O(N),空间复杂度为O(1)
class Solution:
def majorityElement(self, nums: List[int]) -> int:
res = nums[0]
count = 1
for i in range(1, len(nums)):
if count==0:
res = nums[i]
if nums[i]==res:
count += 1
else:
count -= 1
return res215. 数组中的第K个最大元素
题解:
方法一:基于快速排序的选择方法
比基准大的放在左边,比基准小的放在右边。
class Solution:
def findKthLargest(self, nums, k):
if len(nums)==1:
return nums[0]
def quicksort(low, high):
i,j = low, high
pivot = nums[i]
while i=pivot:
i += 1
nums[i], nums[j] = nums[j], nums[i]
nums[i], nums[low] = nums[low], nums[i]
if i==k-1:
return nums[i]
elif i>k-1:
return quicksort(low, i-1)
else:
return quicksort(i+1, high)
return quicksort(0, len(nums)-1) 由于只需要在一个分支递归,所以时间复杂度为O(N),优于原始的快速排序。
时间复杂度为O(N),空间复杂度为O(logn),因为递归使用栈空间的空间代价的期望为O(logn)
方法二:堆排
topk问题使用最小堆,堆中的k个节点代表着当前最大的k个元素,而堆顶是这k个元素中的最小值。
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
n = len(nums)
heap = nums[:k]
def heapify(pos):
while 2*pos + 1 < k:
childindex = 2*pos + 1
left, right = 2*pos + 1, 2*pos + 2
if rightheap[childindex]: #如果父节点大于任何一个子节点,则交换 (堆顶元素大于当前元素值)
heap[pos], heap[childindex] = heap[childindex], heap[pos]
pos = childindex
else:
break
for i in range(k//2, -1, -1):
heapify(i)
for i in range(k,n): #从k开始往后遍历,如果大于堆顶,则进行替换,并对堆重新进行调整
if heap[0] 建堆的时间复杂度为O(K), 遍历剩余数组的时间复杂度为O(n-k),每次调整堆的时间复杂度为O(logk),总的时间复杂度为O(nlogk)。
空间复杂度为O(logn),因为递归使用栈空间的空间代价的期望为O(logn)。
560. 和为K的子数组
题意: 找出整数数组中和为k的连续子数组的个数,数组中可能有负数。
题解: 前缀和+字典
构建前缀和数组,用来快速计算区间和;若cur_sum - k存在于字典中,则说明当前累加值减去前面得到的某一累加值可以得到目标和。
由于只关心次数,而不需要具体的解,因此可以使用哈希表来加速运算。
字典d中的key为前缀和,value为该前缀和出现的次数。
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
n = len(nums)
res = 0
d = collections.defaultdict(int)
cur_sum = 0
for i in range(n):
cur_sum += nums[i] # 计算当前的前缀和
if cur_sum==k:
res += 1
if cur_sum - k in d: #当前的前缀和减去K,则为之前的前缀和,查看是否字典存在
res += d[cur_sum-k]
d[cur_sum] += 1
return res
时间复杂度降到了O(N), 空间复杂度为O(N)。未排序数组中累加和为给定值k的最长子数组的长度
题意:数组中元素可正、可负、可0,给定一个整数k,求arr所有子数组中累加和为k的最长子数组的长度。
题解:前缀和的思想,s[i] 表示arr[0...i]的和,则s[j+1....i] = s[i] - s[j],假设遍历到位置i,若我们能找到前面的和(s[j])为 s[i]-k,则s[j+1....i] = k。
使用字典存储前i项和及其对应下标
其中初始字典为{0: -1},当数组是从0开始的累加和为k时,就会用到
def function(arr, k):
n = len(arr)
d = {0:-1}
res = 0
cur_sum = 0
for i in range(n):
cur_sum += arr[i]
if cur_sum not in d.keys():
d[cur_sum] = i
if cur_sum - k in d.keys():
res = max(res, i-d[cur_sum-l])
return res0与1个数相等的最长子数组
题意:有一个无序数组,只包含0或1,找出数组的所有子数组中0和1的个数相等的最长子数组的长度。
题解:
把0变为-1,然后题目就变为了寻找子数组和为0的最大长度。
def function(arr, k):
n = len(arr)
d = {0:-1}
res = 0
cur_sum = 0
for i in range(n):
if arr[i]==0: # 将0修改为-1
arr[i]=-1
cur_sum += arr[i]
if cur_sum not in d.keys():
d[cur_sum] = i
if cur_sum - k in d.keys():
res = max(res, i-d[cur_sum-l])
return resN数之和系列
15. 三数之和
题意:
给你一个包含 n 个整数的数组 nums,判断nums中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。注意:答案中不可以包含重复的三元组。
题解:双指针
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
if n<3:
return []
nums.sort() # 先进行排序
res = []
for i in range(n):
if nums[i]>0:
return res
if i>=1 and nums[i]==nums[i-1]: # 相同元素直接跳过
continue
left, right = i+1, n-1
while left0:
right -= 1
if s<0:
left += 1
return res 18. 四数之和
题意:给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。
注意:答案中不可以包含重复的四元组。
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]题解:双指针的思想
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
n = len(nums)
nums.sort()
if n<4:
return []
res = []
for i in range(n-3):
if i > 0 and nums[i] == nums[i-1]:
continue
for j in range(i+1, n):
if j>i+1 and nums[j]==nums[j-1]:
continue
left, right = j+1, n-1
while left4. 寻找两个正序数组的中位数
题解:要求时间复杂度为O(log(m+n))
二分查找
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
def getK(nums1, nums2, k): # 寻找第K小的数
if len(nums1) =nums2[t-1]:
return getK(nums1, nums2[t:], k-t)
else:
return getK(nums1[t:], nums2, k-t)
k1 = (len(nums1) + len(nums2)+1)//2
k2 = (len(nums1) + len(nums2)+2)//2
return (getK(nums1, nums2, k1) + getK(nums1, nums2, k2))/2 162. 寻找峰值
题意:峰值元素是指其值大于左右相邻值的元素。
给你一个输入数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
题解:数组两端认为是负无穷,而数组的值是确定的整型数,必然不会是正无穷,这说明数组中必定能找到一个峰值
方法一:暴力法,时间复杂度为O(N)
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
nums = [-float('inf')] + nums + [-float('inf')]
n = len(nums)
for i in range(n):
if nums[i]>nums[i-1] and nums[i]>nums[i+1]:
return i-1方法二:二分查找,时间复杂度为O(logN);首先从数组中找到中间元素mid,若该元素恰好位于降序序列或者一个局部下降中,则说明峰值在本元素的左侧,可以缩小空间;若位于上升序列,则说明峰值在右侧。
class Solution:
def findPeakElement(self, nums: List[int]) -> int:
# 二分查找
nums.append(-float("inf"))
n = len(nums)
left, right = 0, n-1
while leftnums[mid+1]:
right = mid
return left 189. 旋转数组
题意:给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
题解: 3次旋转
先翻转[0, n-k-1]的部分
然后再翻转[n-k, n-1]的部分
最后再整体翻转。
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
def reverse(i,j):
while i153. 寻找旋转排序数组中的最小值
题意:已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
题解:二分查找
class Solution:
def findMin(self, nums: List[int]) -> int:
n = len(nums)
i,j = 0, n-1
while i154. 寻找旋转排序数组中的最小值 II
题意:和剑指 Offer 11. 旋转数组的最小数字是一个题目,和上题的区别在于,数组中的元素是可能存在重复的。
题解:区别就在于相等时候的处理
class Solution:
def findMin(self, nums: List[int]) -> int:
n = len(nums)
i,j = 0, n-1
while inums[j]:
i = mid+1 # 右侧必定有最小值,因此可以大胆+1
else: # 当相等时,向左缩小空间
j -= 1
return nums[i] 33. 搜索旋转排序数组
题意:给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
题解:
class Solution:
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
low, high = 0, len(nums)-1
while low<=high:
mid = low + (high-low)//2
if nums[mid]==target:
return mid
if nums[0]<=nums[mid]: # (0, mid)升序
if nums[0]<=target378. 有序矩阵中第 K 小的元素
题意:给你一个 n x n 矩阵 matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
题解:
class Solution:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
n = len(matrix)
def check(mid):
i,j = n-1,0 # 从左下角开始
num = 0
while i>=0 and j=k
left, right = matrix[0][0], matrix[-1][-1] # 二分查找
while left 给定一个只读数组 l,长度是M,最小值是a,最大值是b,l 中的元素两两各不相等。给定内存 O(N) << M, 要求找出 l 的中位数
题解:二分查找
def find(nums, a, b):
mid = (a+b)//2
while 1:
less, more = 0, 0
for num in nums:
if num>mid:
more += 1
elif nummore:
mid = (a+mid)//2 # 中位数要小于mid
else:
mid = (b+mid)//2 # 中位数要大于mid
使用rand5()生成rand7()
def Rand7():
x = float('inf') // max int
while(x > 21)
x = 5 * (Rand5() - 1) + Rand5() // Rand25
return x%7 + 141. 缺失的第一个正数
题意: 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
题解:原地修改数组来代替使用哈希表。
对于一个长度为N的数组,其中没有出现的最小正整数只能在[1, N+1],因为如果[1, N]都出现了,那么答案就是N+1,否则答案就是[1, N]中没有出现的最小正整数。
1、首先把不在[1, N]范围内的数修为任意一个大于N的数,如N+1。从而使得所有的数均为正数。
2、遍历数组中的每个数x,它可能已经被打了标记,因此原本对应的数为|x|,若|x|为[1, N]之间,则我们给数组中的第|x|-1个位置的数添加一个负号,若其已经有负号,则不需要重复添加。
3、遍历完成后,若数组中的每一个数都是负数,则答案是N+1,否则答案是第一个正数的位置下标+1。
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
n = len(nums)
for i in range(n):
if nums[i]<=0:
nums[i] = n+1
for i in range(n):
index = abs(nums[i])
if index<=n and nums[index-1]>0:
nums[index-1] *= -1
for i in range(n):
if nums[i]>0:
return i+1
return n+1448. 找到所有数组中消失的数字
题意:
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。 要求时间复杂度为O(N),空间复杂度为O(1)
题解:
第一次遍历,我们假设数组中的元素是一个位置索引,例如元素1对应位置索引0、元素6对应位置索引5,以此类推,然后我们将对应位置索引的数组元素变为负数,那么遍历完这一遍之后数组中只有缺失数对应的位置索引处的元素为正;
第二次遍历,找到数组中正元素位置处对应的索引,然后加1将其放入结果数组即为最终结果。
class Solution:
def findDisappearedNumbers(self, nums: List[int]) -> List[int]:
res = []
for n in nums:
index = abs(n)-1
if nums[index]>0:
nums[index] *= -1
for index, e in enumerate(nums):
if e>0:
res.append(index+1)
return res不同路径
62. 不同路径
题意:
求机器人从左上角走到右下角有多少条不同的路径,每次只能往下或往右移动一步。
题解:
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[0]*n for _ in range(m)]
for i in range(n):
dp[0][i] = 1
for j in range(m):
dp[j][0] = 1
for i in range(1,m):
for j in range(1,n):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[m-1][n-1]63. 不同路径 II
题意: 不同之处在于出现了障碍物,要求返回从左上到右下的路径条数
题解:动态规划
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m,n = len(obstacleGrid), len(obstacleGrid[0])
dp = [[0]*(n) for _ in range(m)]
dp[0][0] = 1 if obstacleGrid[0][0] != 1 else 0
if dp[0][0] == 0: return 0 # 如果第一个格子就是障碍,return 0
for i in range(1,m):
if obstacleGrid[i][0]==1:
dp[i][0] = 0
else:
dp[i][0] = dp[i-1][0]
for j in range(1,n):
if obstacleGrid[0][j]==1:
dp[0][j] = 0
else:
dp[0][j] = dp[0][j-1]
for i in range(1,m):
for j in range(1, n):
if obstacleGrid[i][j]==1:
dp[i][j] = 0
else:
dp[i][j] = dp[i-1][j]+dp[i][j-1]
return dp[-1][-1]面试题 08.02. 迷路的机器人
题意:要求返回一条可行的路径
题解:若是要求出路径,则需要使用回溯的思想
class Solution:
def pathWithObstacles(self, obstacleGrid: List[List[int]]):
r, c = len(obstacleGrid), len(obstacleGrid[0])
if r<1:
return []
def dfs(x,y, visited):
if x==r-1 and y==c-1 and obstacleGrid[x][y]==0:
return [[x,y]]
if 0<=x64. 最小路径和
题意:
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。说明:每次只能向下或者向右移动一步。
题解:
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
row, col = len(grid), len(grid[0])
dp = [[0]*col for _ in range(row)]
dp[0][0] = grid[0][0]
for i in range(1,row):
dp[i][0] = dp[i-1][0] + grid[i][0]
for j in range(1, col):
dp[0][j] = dp[0][j-1] + grid[0][j]
for i in range(1,row):
for j in range(1, col):
dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
return dp[-1][-1]若要求路径,则需要改为
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
row, col = len(grid), len(grid[0])
res = []
def dfs(i,j, path, s): # path为具体的路径,s为当前的路径之和
if not 0<=i|
174. 地下城游戏
题意:
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
例如,考虑到如下布局的地下城,如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下,则骑士的初始健康点数至少为 7。
-2 (K) -3 3
-5 -10 1
10 30 -5 (P)
题解:
从右下角往左上角递推,dp[i][j]表示到达(i, j)所需的最小生命值。
class Solution:
def calculateMinimumHP(self, dungeon: List[List[int]]) -> int:
m,n = len(dungeon), len(dungeon[0])
dp = [[0]*n for _ in range(m)]
dp[-1][-1] = max(1, 1-dungeon[-1][-1])
for i in range(n-2, -1, -1): # 初始化最后一行
dp[-1][i] = max(1, dp[-1][i+1] - dungeon[-1][i])
for j in range(m-2, -1, -1): # 初始化最后一列
dp[j][-1] = max(1, dp[j+1][-1] - dungeon[j][-1])
for i in range(m-2, -1, -1):
for j in range(n-2, -1, -1):
minn = min(dp[i+1][j], dp[i][j+1]) # 正下方和右方所需的最小生命值中的较小值
dp[i][j] = max(minn - dungeon[i][j], 1)
return dp[0][0]https://leetcode-cn.com/problems/dungeon-game/solution/dong-tai-gui-hua-zi-di-xiang-shang-python3-by-zhu_/
120. 三角形最小路径和
题意:
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
题解:
方法一:自上而下
dp[i][j]表示到达(i, j)的最小路径和,而要走到(i, j),上一步就只能在(i-1, j)或者(i-1, j-1),状态转移方程为 dp[i][j]=min(dp[i−1][j−1], dp[i−1][j])+c[i][j]
此外,在最左端和最右端需要另外处理
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
n = len(triangle)
if n==1:
return triangle[0][0]
dp = [[0]*n for _ in range(n)]
dp[0][0] = triangle[0][0]
for i in range(1,n):
dp[i][0] = dp[i-1][0]+triangle[i][0] # 最左端
for j in range(1, i):
dp[i][j] = min(dp[i-1][j], dp[i-1][j-1])+triangle[i][j]
dp[i][i] = dp[i-1][i-1]+triangle[i][i] # 最右端
return min(dp[-1])空间复杂度为O(N^2)
方法二:
自下而上 + 空间优化
自下而上时,dp[i][j]表示从(i,j)到最底下的最小路径和,转移方程为dp[i][j] = min(dp[i+1][j+1],dp[i+1][j]) + triangle[i][j]
可以优化为一维数组,dp[j] = min(dp[j],dp[j+1]) +triangle[i][j]
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
n = len(triangle)
if n==1:
return triangle[0][0]
dp = [0]*(n+1)
for i in range(n-1, -1, -1):
for j in range(i+1):
dp[j] = min(dp[j], dp[j+1])+triangle[i][j]
return dp[0]空间复杂度为O(N)
283. 移动零
题意:给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 要求:原地操作
题解:
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
i,j = 0, 0
while j剑指 Offer 14- I. 剪绳子
题意:
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m-1] 。请问 k[0]*k[1]*...*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
题解:
方法一:动态规划
dp[i]表示长度为i的绳子,剪成m段之后的最大乘积。从j位置开始剪,剪了第一段之后,剩下的(i-j)可以剪或不剪,取两者的最大值,max( j * dp[i - j], j * (i - j))。
class Solution:
def cuttingRope(self, n: int) -> int:
dp = [0]*(n+1)
dp[2] = 1
for i in range(3,n+1):
for j in range(2, i):
dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]))
return dp[-1]方法二:
贪心法,尽可能地将绳子分成长度为3的小段,这样乘积最大。
class Solution:
def cuttingRope(self, n: int) -> int:
if n < 4:
return n - 1
res = 1
while n > 4:
res *=3
n -= 3
return res * n
300. 最长递增子序列
题意:给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。题解:
动态规划的方法时间复杂度为O(N^2),若要降到O(NlogN),则需要使用贪心+二分查找的思想。
新建一个数组,用于保存最长上升子序列。对原序列进行遍历,将每位元素二分插入到新数组中,若新数组中的元素都比它小,则将它插入到最后;否则,用它覆盖掉比它大的元素中最小的那个。
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
res = []
for n in nums:
if not res or n>res[-1]:
res.append(n)
else:
l,r = 0, len(res)-1
loc = 0
while l<=r:
mid = (l+r)//2
if n<=res[mid]:
loc = mid
r = mid -1
else:
l = mid +1
res[loc] = n # 覆盖
return len(res)673. 最长递增子序列的个数
题意:给定一个未排序的整数数组,找到最长递增子序列的个数。
题解:
相比上题,相当于是增加了一个计数器,使用动态规划的思想,dp[i]表示nums中到第i个元素为止的最长递增子序列的长度。count[i]表示nums中到第i个元素为止的最长递增子序列的个数。
对于每一个数nums[i],若其之前的数nums[j] 所以,在nums[i] > nums[j]的大前提下:1、如果dp[j] + 1 > dp[i],说明最长递增子序列的长度增加了,dp[i] = dp[j]+1,长度增加,数量不变 count[i] = count[j];2、如果dp[j]+1==dp[i],说明最长递增子序列的长度并没有增加,但是出现了长度一样的情况,数量增加 count[i] += count[j]。然后不断记录最长递增子序列的最大长度。最后,遍历dp数组,若dp数组记录的最大长度等于max_len,则将其对应的数量count[i]加入到结果中。 题意:给定一个整数数组 题解: 动态规划:定义dp[i] 为nums[i]这个数结尾的最大子数组和 数学归纳法:当已知dp[i-1]时,要得到dp[i],dp[i]有两种选择,一是和前面的相邻子数组连接;二是自成一派(dp[i-1]<0,nums[i]>0时)。因此,取这两者的最大值。 dp[i] = max(nums[i], nums[i] + dp[i-1]) 题意:给两个整数数组 题解: 对于两个字符串的动态规划问题,套路是通用的。 一、对于s1和s2,一般来说都要构造一个这样的DP Table: dp[i][j]的含义就是对于s1[1..i]和s2[1..j],它们的最长公共子数组长度是dp[i][j],dp[2][4] 的含义就是:对于 "ac" 和 "babc",它们的 LCS 长度是 2。 定义dp[i][j]为以下标 i 为结尾的A和以下标 j 为结尾的B的最长重复子数组的长度。 和最长公共子串是一样的题目。 题意: 循环有序指的是数组是有序的,但是两个端点不一定是最小值和最大值。如[12,16,20,3,5,9] 题解: 由于是循环有序的数组,存在一边有序的情况,从中间进行切分,一定分成一个有序数组和一个循环有序数组。 判断一个整数数组内是否有重复元素,要求时间复杂度为O(N),空间复杂度为O(1) 题解: 如果元素的范围未知,可以申请常数大小的空间,由于int最大表示范围是65536,我们可以直接申请 题意:给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 题解:最短边决定了能接到多少水,因此优先考虑短边,短边先移动。使用双指针的思想,空间复杂度为O(1)。 在动态规划方法中,需要维护两个数组,空间复杂度是O(N),下标i处能接的雨水量是由leftmax[i]和rightmax[i]中的最小值决定的,由于leftmax是从左往右计算,而rightmax是从右往左计算,因此可以使用双指针left, right和两个变量leftmax, rightmax来代替两个数组。 在移动两个指针的过程中维护两个变量的值。 题意: 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。 题解:由于硬币的数量是无限的,因此是个完全背包问题 外循环nums,内循环target, target正序且target>=nums[i] dp[i]表示总金额为i时的最少硬币个数 题意: 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整数。 题解:本题的不同之处是要求的是组合数,是个组合问题+完全背包问题。 dp[i] += dp[i-num] 注意:组合是不强调元素之间的顺序的,而排列数是强调元素之间的顺序。dp[i]表示是金额之和为i时,硬币的组合数,dp[0]=1,即当金额之和为0时,只有1种组合,即不选取任何硬币。 如果求组合数就是外层for循环遍历物品,内层for遍历背包。这样就不会出现重复计算。 如果求排列数就是外层for遍历背包,内层for循环遍历物品。 题意:给定正整数 n,找到若干个完全平方数(比如 题解:完全背包问题 最小值 题意: 在n+1个整数的数组中,数字都在1到n之间,至少存在一个重复的整数,找出该整数。要求必须不修改原数组,且使用常数量级O(1)的额外空间。 题解: 方法一:二分查找,二分法确定一个有范围的整数。 先猜一个中间数mid,统计小于等于mid的元素个数count,若count>mid,则说明重复元素在[left, mid],缩小范围。 时间复杂度O(NlogN),空间复杂度O(1) 方法二: 快慢指针的思想,将数组看做为一个链表,下标为当前指针(node),值指向下一指针(nextnode);若有重复的数字说明有两个指针的nextnode相同。首先需要先找到环的入口,然后将slow指针放在起点0处,然后两个指针同时移动一步,相遇点就是答案。 时间复杂度O(N),空间复杂度O(1) 题解:遍历数组,假设第i个位置的数字为j,则通过交换将j换到下标为j的位置上, 直到所有数字都出现在自己对应的下标处,或发生了冲突。 时间复杂度O(n),空间复杂度O(1) 题意:给定一个不含重复数字的数组 题解:回溯法 可以看做是有 n 个排列成一行的空格,我们需要从左往右依此填入题目给定的n个数,每个数只能使用一次。因此,可以从左往右每一个位置都依此尝试填入一个数,看能不能填完这 n 个空格。 定义回溯函数为trace_back(cur, ind),分别表示当前排列和填到了第ind个位置。 或者方法二: 题意: 给定一个可包含重复数字的序列 题解: 方法一:可以按照上题的思路 或者方法二: 题意: 实现获取 下一个排列 的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。必须原地修改,只允许使用额外常数空间。 题解: 两遍扫描,双指针 我们需要找到一个大于当前序列的新序列,且变大的幅度要尽可能地小。 1、因此,需要先将一个左边的“较小数”与一个右边的“较大数”交换,使得当前排列变大,从而得到下一个排列。 2、同时,要让这个“较小数”尽量靠右,而“较大数”尽可能小。交换完成后,“较大数”右边的数需要按照升序重新排列。这样保证新排列变大的幅度尽可能小。 时间复杂度为O(N),空间复杂度为O(1) 题意: 给定一个整数 n, 返回从 1 到 n 的字典顺序。 例如,给定 n =1 3,返回 [1,10,11,12,13,2,3,4,5,6,7,8,9] 。 请尽可能的优化算法的时间复杂度和空间复杂度。 输入的数据 n 小于等于 5,000,000。 题意: 输入:grid = [ 题解: 题意: 找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 题解: 相比上题,就是增加了一个变量self.size。 题意: 在网格中,只有一个岛屿,求出该岛屿的周长。 题解: 对于每个方格,依次进行遍历,找到陆地,计算其上下左右的情况: 1、若遇到水域或出界,边+1 2、若遇到陆地,将其标记为2,不加。 题意: 给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。 题解: 由于candidates中没有重复数,因此,从前往后遍历就不会有重复解。 题意:与上一题不同的是,candidates中有重复数字, 题解: 为了避免产生重复解,需要先对candidates排序。 for循环遍历从ind开始的数,选择一个数进入下一层递归。若从ind开始的数有连续出现的重复数字,跳过该数字continue。(防止出现重复解)因为数字不可以重复选择,所以在进入下一层递归时,i要加1,从i之后的数中选择接下来的数。 题意: 给定一个非负整数数组 题解: 贪心:实时维护可以到达的最远距离 题意:假设你总是可以到达数组的最后一个位置。要求求出最少的跳跃次数 题解: 题意:将上述两题进行结合,如果能够跳跃到最后一个位置,返回最少跳跃次数;如果跳跃不到最后一个位置,返回 False。 题解: 遍历数组的每一个元素(包括最后一个元素),如果当前遍历位置已经超过了所能到达的最远位置(maxPos),那么说明不能到达最后一个数组位置,返回False; 题意: 这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。 请你判断自己是否能够跳到对应元素值为 0的任一 下标处。 注意,不管是什么情况下,你都无法跳到数组之外。 题解: 广度优先搜索,得到从start开始能够到达的所有位置,若某个位置对应的元素值为0,则返回True。 题意:给定一个数组 题解:贪心,动态维护最小值和最大利润。 题意:与上题的区别在于,这题可以尽可能多地完成交易(前提是在再次购买前出售掉之前的股票)即不限交易次数 题解:方法一:二维dp dp为利润情况 两个维度分别是天数和是否持有股票(1表示持有,0表示不持有)。 第i天的状态转移方程为 dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]) #今天没有股票有两种可能:1、昨天就没有这个股票,今天没有任何操作。 2、昨天就有股票,今天卖掉了,收获了一笔钱。 dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]) #今天持有股票有两种可能:1、昨天就有这个股票,今天没有任何操作。 2、昨天没有股票,今天买入了,花掉了一笔钱。 方法二:直接贪心算法 对于连续上涨交易日:第一天买、最后一天卖的收益最大,即pn-p1,等价于每天都买卖,即pn-p1 = (p2-p1)+(p3-p2)+...+(pn-pn-1) 遍历整个价格列表,tmp = prices[i] - prices[i-1],当tmp>0时(利润为正时),加入到最后的利润res之中。 题意:与121题目不同的是:最多可以完成两笔交易 题解: 方法一: 三维DP 交易次数作为一个新的维度考虑进dp table中,三个维度分别是 天数(i),买入股票的次数j(j=1,2,...k), 是否持有股票(1表示持有,0表示不持有)。 dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i]) # max()的第二项:今天卖了昨天持有的股票,所以两次买入股票的次数都是j dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i]) # max()的第二项:昨天没有持有而今天买入一只,所以昨天的次数是j-1 边界状态:考虑 i=0和 j=0 方法二: 在第二次购买的时候,价格其实是考虑用了第一次赚的钱去补贴一部分的 buy1是第一次买卖的成本、buy2是第二次买卖的成本(注意:是第二次买入股票的价格减去第一次的收益)。 pro1是第一次买卖的收益、pro2是两次买卖的总收益。 题意:最多进行k次交易,k为输入值 题解: 有效的交易是由买入和卖出构成的,至少需要两天。所以,若题目给出的最大交易次数k<=n/2时,这个k是可以有效约束交易次数的;若k>n//2,则这个k实际上起不到约束的作用,可以认为k='+inf',本题退化为122题。 因此,本题可以根据k和n/2的大小关系来分为两个分支去处理。 题意:在卖出股票后,有冷冻期1天,冷冻期之后才能买入新的股票 题解: 题意:给定圆的半径和圆心的 x、y 坐标,写一个在圆中产生均匀随机点的函数 题解: 拒绝采样,使用边长为2R的正方形盖住圆,并在正方形内随机生成点。 由于正方形的面积为 (2R)^2 = 4R^2 ,圆的面积为 π R^2,因此在正方形中随机生成的点,落在圆内的概率为 Pr(x) = πR^2/4R^2 ≈0.785,因此期望的生成次数为E= 1/0.785 ≈1.274。 以单位圆为例,最后再将圆心平移、半径乘以相应的倍数。 题意: 给定一组非负整数 注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。 题解:此题和剑指 Offer 45. 把数组排成最小的数基本上是一样的 方法一:利用python的functools中的cmp_to_key函数,先自定义比较函数,再按照这个比较函数对字符串进行排序。 方法二:快排 题意: 你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。判断是否可能完成所有课程的学习? 输入:numCourses = 2, prerequisites = [[1,0]] 题解: 广度优先搜索 题意:给定课程总量以及它们的先决条件,返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。 输入: 4, [[1,0],[2,0],[3,1],[3,2]] 题解: 题意: 给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。求在该柱状图中,能够勾勒出来的矩形的最大面积。 题解: 核心是求左边第一个比i小的和右边第一个比i小的。 保存的是下标 维护一个单调递增栈,若新元素比栈顶元素大,则入栈;若新元素小于栈顶,就一直把栈内元素pop出来,直到栈顶比新元素小。 当元素出栈时,说明这个新元素是出栈元素向后找到的第一个比其小的元素。 当元素出栈后,说明新的栈顶元素是出栈元素向前的第一个比其小的元素。 题意:给定一个仅包含 题解:参照着84题,把二维矩阵逐行遍历,构造成柱状图,即可使用84题的代码进行复用。 题意:在一个由 题解: 动态规划,dp[i][j]表示以(i, j)为右下角,且只包含1的正方形的边长最大值。 当matrix[i][j]=='0'时,dp[i][j]=0; 当matrix[i][j]=='1'时,若i==0 或j==0,即处于边界时,正方形大小只能为1;否则的话,正方形的大小由(i,j)的左上方、左方和上方的三个方向的dp最小值决定。 题意:给你一个整数数组 nums ,数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成,并同时满足:i < j < k 和 nums[i] < nums[k] < nums[j] 。 如果 nums 中存在 132 模式的子序列 ,返回 true ;否则,返回 false 。 题解: 先得到一个数组leftmin,表示数组中某元素前面的最小值,再维护一个单调递减栈,确定3和2,最后再比较leftmin和2即可。 时间复杂度O(N),空间复杂度O(N) 题意:给你两个 没有重复元素 的数组 请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。 nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。 输入: nums1 = [2,4], nums2 = [1,2,3,4]. 你可以设计一个时间复杂度为 题解:栈的思想 nums1是nums2的子集,因此,我们可以先只考虑nums2,遍历nums2,对于每一个元素,求出其下一个更大的元素,然后将这些答案放入一个哈希表中(字典),key=元素值,value=元素的下一个更大的元素值;对于nums1来说,只需要去查找字典即可得到答案。 具体来说,当栈是空时或者当前值大于栈顶元素时,将栈顶元素出栈,并将其保存到字典中;然后将当前值入栈。若当前值小于栈顶元素,则直接入栈。 题意:给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。 初始化nums1和nums2的元素数量分别为 m 和 n 。你可以假设nums1的空间大小等于m+n,这样它就有足够的空间保存来自 nums2 的元素。 要求原地修改 题解: 双指针的思想,不过是从后往前遍历 其实需要3个指针 题意:在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。 题解: 归并排序,在合并的过程中(合并两个排序数组)统计逆序数,每当遇到左子数组的当前元素>右子数组的当前元素时,意味着“左子数组当前元素至末尾元素”与“右子数组的当前元素”构成了若干逆序对。 题意: 与剑指 Offer 41. 数据流中的中位数是同一个题 中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。 例如,[2,3,4] 的中位数是 3,[2,3] 的中位数是 (2 + 3) / 2 = 2.5 设计一个支持以下两种操作的数据结构: void addNum(int num) - 从数据流中添加一个整数到数据结构中。 题解: 最容易想到的是,数据流新进来一个数,就把它和已有的数据进行一次排序,就可以得到中位数。但是缺点是,每进行一次排序,时间复杂度为O(NlogN)。事实上,我们只对中位数感兴趣,对于其他位置的元素并不关心。 由于只关心在中间的两个数(或一个数),堆(优先队列)具有这样的性质,每次都从堆里得到一个最值,而其他元素无需比较,可以以O(logN)的复杂度每次从堆中取出最值。 因此无论两个堆的元素个数之和是奇数或者是偶数,都得先「最大堆」 再「最小堆」 ,而当加入一个元素之后,元素个数为奇数的时候,再把最小堆的堆顶元素拿给最大堆就可以了。将元素放入优先队列以后,优先队列会自行调整(以对数时间复杂度),把最优值放入堆顶,是这道问题思路的关键。 题意:对于给定的整数 n, 如果n的k(k>=2)进制数的所有数位全为1,则称 k(k>=2)是 n 的一个好进制。 以字符串的形式给出 n, 以字符串的形式返回 n 的最小好进制。 题解: https://leetcode-cn.com/problems/smallest-good-base/solution/python-ren-xing-de-py100-by-qubenhao-6kvg/ 题意:给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。 题解: 队列的思想,即先进先出 题意: 给你一个字符串 题解:滑动窗口的思想 1、首先初始化两个指针,left=right=0,minlen=float('inf'), need字典为T中各个字符及其对应的个数。 2、然后不断增加right指针,以扩大窗口,直到窗口中的字符串满足要求(包含了T中所有的字符)即 counter==0 3、此时,我们停止增加right,转而不断增加left指针以缩小窗口,直到窗口中的字符串不符合要求,即遇到了一个必须包含的元素(不包含T中的所有字符)即 need[s[i]]==0 重复上述步骤,直到right达到S的尽头。 题意:假设你有两个数组,一个长一个短,短的元素均不相同。找到长数组中包含短数组所有的元素的最短子数组,其出现顺序无关紧要。 返回最短子数组的左端点和右端点,如有多个满足条件的子数组,返回左端点最小的一个。若不存在,返回空数组。 题解:和上题的思路一致,但是只需要保留左端点即可。 题意:给你一个字符串 题解: 双指针从中心扩散法:从每一个位置出发,向两边扩撒即可,遇到不是回文时结束。 题意: 给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。 具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。 题解: dp[i][j]表示子串[i, j]是否是一个回文串 题意: 编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀,返回空字符串 题解: 题意:给定一个只包括 题解: 遍历字符串 s :如果当前字符是左括号,入栈;如果当前字符是右括号,将栈顶的第一个元素出栈,观察左右括号是否匹配,如果匹配继续遍历,如果不匹配提前结束遍历返回 False; 题意: 给定一个只包含三种字符的字符串:( ,) 和 *,写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则: 任何左括号 ( 必须有相应的右括号 )。 题解: 题意:数字 题解:回溯算法 题意:给你一个只包含 我们利用两个计数器left 和right 。首先,我们从左到右遍历字符串,对于遇到的每个 ‘(’,我们增加 left 计数器,对于遇到的每个 ‘)’ ,我们增加 right 计数器。每当 left 计数器与 right 计数器相等时,我们计算当前有效字符串的长度,并且记录目前为止找到的最长子字符串。当 right 计数器比 left 计数器大时,我们将 left 和 right 计数器同时变回 0。 这样的做法贪心地考虑了以当前字符下标结尾的有效括号长度,每次当右括号数量多于左括号数量的时候之前的字符我们都扔掉不再考虑,重新从下一个字符开始计算,但这样会漏掉一种情况,就是遍历的时候左括号的数量始终大于右括号的数量,即 (() ,这种时候最长有效括号是求不出来的。 解决的方法也很简单,我们只需要从右往左遍历用类似的方法计算即可,只是这个时候判断条件反了过来: 当 left 计数器比 right 计数器大时,我们将left 和 right 计数器同时变回 0 时间复杂度O(N) 空间复杂度为O(1) 题意:给你两个单词 你可以对一个单词进行如下三种操作: 题解: dp[i][j]表示word1到i位置的前面所有元素转换为word2到j位置的前面所有元素所需要的最少步数。 题意:版本号由一个或多个修订号组成,各修订号由一个 题解: 将字符串转换为整数 题意: 字符串压缩。利用字符重复出现的次数,编写一种方法,实现基本的字符串压缩功能。比如,字符串aabcccccaaa会变为a2b1c5a3。若“压缩”后的字符串没有变短,则返回原先的字符串。你可以假设字符串中只包含大小写英文字母(a至z)。 题解: 题意: 给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。 字符串的一个 子序列 是指,通过删除一些(也可以不删除)字符且不干扰剩余字符相对位置所组成的新字符串。 题解: 动态规划,dp[i][j]表示在s[i:]中t[j:]出现的个数。 当s[i]==t[j]时,t[j]有两种选择:1、选择匹配,dp[i][j] = dp[i+1][j+1];2、选择不匹配,则有dp[i][j] = dp[i+1][j];因此dp[i][j] = dp[i+1][j+1] + dp[i+1][j] 当s[i]!=t[j]时,dp[i][j] = dp[i+1][j] 题意:给你两个字符串 a 和 b,请你在 a 字符串中找出 b字符串出现的第一个位置(下标从 0 开始)。如果不存在,则返回 -1 。 题解: 方法一:暴力 时间复杂度为O(N*M) 方法二:KMP 当出现字符串不匹配时,可以记录一部分之前已经匹配的文本内容,利用这些信息避免从头再去做匹配。 前缀表:记录下标i之前的字符串中(包含i),有多大长度的相同前缀后缀。 前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串;后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。 当找到不匹配的位置时,查看前一位的前缀表的数值,并把下标移动到这个数值的下标。这个前缀表是在模式串上计算得到的。 next数组就是前缀表,实现的时候将前缀表统一减1(右移一位,初始位置为-1) 时间复杂度为O(N+M) 题意:给你一个字符串 题解:递归遍历子串,然后判断子串是否是回文串,若是,则保存。 题意: 给定一个只包含数字的字符串,用以表示一个 IP 地址,返回所有可能从 s 获得的 有效 IP 地址 。你可以按任何顺序返回答案。 有效 IP 地址 正好由四个整数(每个整数位于0 到 255之间组成,且不能含有前导 0),整数之间用 '.' 分隔。 例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "[email protected]" 是 无效 IP 地址。 题解:回溯思想 判断子串是否合法:段位以0开头的数字不合法; 段位里字符是零,但不止一个零则不合法; 段位如果不在0~255就不合法。 题意:一条包含字母 A-Z 的消息通过以下映射进行了 编码 : 'A' -> 1 给你一个只含数字的 非空 字符串 题解: 动态规划,dp[i]表示字符串s的前i个字符的解码方法数。对于dp[i]来说,有两种情况:1、使用了一个字符,即s[i]进行解码,只要s[i]不等于0,则有dp[i]=dp[i-1];2、使用了2个字符,即s[i-1]和s[i]进行解码,其中s[i-1]不等于0,并且,s[i-1]和s[i]组成的整数必须小于等于26,这样两者才能解码。dp[i]=dp[i-2]。 将上述两种状态转移方程在对应的条件下进行累加,即可得到dp[i]的值。 其中,边界条件为dp[0] = 1 爬楼梯 题意: 给你一个字符串 s 和一个字符串数组 dictionary 作为字典,找出并返回字典中最长的字符串,该字符串可以通过删除 s 中的某些字符得到。 如果答案不止一个,返回长度最长且字典序最小的字符串。如果答案不存在,则返回空字符串。 题解: 双指针的思想 题意:给定三个字符串 题解:动态规划,dp[i][j]表示s3的前i+j个字符是否由s1的前i个字符和s2的前j个字符组成。dp[0][0]一定为true。初始化第一列(s1的前 i 位能够构成s3的前 i 位的条件是 前 i-1 位可以构成s3的前 i-1 位且s1的第 i 位等于s3的第 i 位)和第一行。 题意: 给定一个字符串 s 和一些 长度相同 的单词 words 。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。 注意子串要与 words 中的单词完全匹配,中间不能有其他字符 ,但不需要考虑 words 中单词串联的顺序。 题解:滑动窗口+字典class Solution:
def findNumberOfLIS(self, nums: List[int]) -> int:
n = len(nums)
if n==1:
return 1
dp = [1]*n
count = [1]*n
max_len = 0
for i in range(1,n):
for j in range(i):
if nums[i]>nums[j]:
if dp[j]+1==dp[i]: # 当前长度等于历史最佳长度
count[i] += count[j] #更新个数
if dp[j]+1>dp[i]: # 当前长度>历史最佳长度
dp[i] = dp[j]+1 # 这一步相当于 dp[i]=max(dp[i], dp[i]+1)
count[i] = count[j]
max_len = max(max_len, dp[i])
res = 0
for i in range(n):
if dp[i]==max_len:
res += count[i]
return res53. 最大子序和
nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。class Solution:
def maxSubArray(self, nums: List[int]) -> int:
if not nums:
return 0
dp = [0]*len(nums)
dp[0] = nums[0]
res = dp[0] # res不能定义为0,因为nums中可能有负数
for i in range(1,len(nums)):
dp[i] = max(dp[i-1]+nums[i], nums[i])
res = max(res, dp[i])
return res718. 最长重复子数组
A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出:3
解释:
长度最长的公共子数组是 [3, 2, 1] 。class Solution:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
a,b = len(nums1), len(nums2)
dp = [[0]*(b+1) for _ in range(a+1)]
for i in range(1, a+1):
for j in range(1, b+1):
if nums1[i-1]==nums2[j-1]:
dp[i][j] = dp[i-1][j-1]+1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[-1][-1]循环有序数组中查找某个数
def find(nums, target):
if not nums or not target:
return -1
low = 0
high = len(nums)
while low42. 接雨水
class Solution:
def trap(self, height: List[int]) -> int:
res = 0
n = len(height)
left, right = 0, n-1
leftmax, rightmax = 0, 0
while left322. 零钱兑换
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [0] +[10001]*amount
for coin in coins:
for i in range(amount+1):
if coin<=i:
dp[i] = min(dp[i], dp[i-coin]+1)
return dp[-1] if dp[-1]!=10001 else -1518. 零钱兑换 II
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [1] + [0]*amount
for c in coins:
for i in range(amount+1):
if i>=c:
dp[i] += dp[i-c]
return dp[-1]279. 完全平方数
1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。输入:n = 13
输出:2
解释:13 = 4 + 9class Solution:
def numSquares(self, n: int) -> int:
dp = [0] + [float('inf')]*n
nums = [i*i for i in range(1, int(n**0.5)+1)]
for num in nums:
for i in range(1, n+1):
if i>=num:
dp[i] = min(dp[i], dp[i-num]+1)
return dp[-1]重复元素
287. 寻找重复数
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
size = len(nums)
l,r = 1, size-1
while lclass Solution:
def findDuplicate(self, nums: List[int]) -> int:
slow = nums[0] #先走一步
fast = nums[nums[0]]
while 1:
slow = nums[slow]
fast = nums[nums[fast]]
if slow==fast:
break
find = 0
while 1:
find = nums[find]
slow = nums[slow]
if slow==find:
return find给定一个长度为N的数组,其中每个元素的取值范围都是0到N-1。判断数组中是否有重复的数字。
def isduplicate(nums):
for i in range(len(nums)):
while nums[i]!=i:
if nums[i]!=nums[nums[i]]:
tmp = nums[i]
nums[i] = nums[nums[i]]
nums[tmp] = tmp
else:
return True
return False
排列问题
46. 全排列
nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
n = len(nums)
visited = [0]*n
def trace_back(cur, ind):
if ind==n:
res.append(cur)
return
for i in range(n):
if visited[i]:
continue # 继续
visited[i] = 1
trace_back(cur+[nums[i]], ind+1)
visited[i] = 0 # 撤销操作
trace_back([],0)
return resclass Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
res = []
n = len(nums)
visited = [0]*n
def trace_back(tmp):
if len(tmp)==n:
res.append(tmp)
return
for i in range(n):
if visited[i]:
continue # 继续
visited[i] = 1
trace_back(tmp+[nums[i]])
visited[i] = 0 # 撤销操作
trace_back([])
return res47. 全排列 II
nums ,按任意顺序 返回所有不重复的全排列。class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
visited = [0]*n
res = []
def trace_back(cur, ind):
if ind==n:
if cur not in res: # 确保不在结果中
res.append(cur)
return
for i in range(n):
if visited[i]==1:
continue
visited[i]=1
trace_back(cur+[nums[i]], ind+1)
visited[i]=0
trace_back([], 0)
return resclass Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
visited = [0]*n
res = []
def trace_back(tmp):
if len(tmp)==n:
res.append(tmp)
return
for i in range(n):
if visited[i]==1 or ( i>0 and nums[i-1]==nums[i] and visited[i-1]==0):
# 1、当前元素被使用过了 2、当当前元素和前一个元素相同,且前一个元素还没有被使用过时,需要剪枝
continue
visited[i]=1
trace_back(tmp+[nums[i]])
visited[i]=0
nums.sort() # 必须要先排序
trace_back([])
return res31. 下一个排列
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
n = len(nums)
i = n-2
while i>=0 and nums[i]>=nums[i+1]: #找到较小数的位置i
i -= 1
if i>=0:
j = n-1
while j>=0 and nums[i]>=nums[j]: #找到较大数的位置j
j -= 1
nums[i], nums[j] = nums[j], nums[i]
left, right = i+1, n-1 # 将倒序的部分正序
while left386. 字典序排数
class Solution:
def lexicalOrder(self, n: int) -> List[int]:
def dfs(num):
if num>n:
return
res.append(num)
for i in range(10):
dfs(num*10 + i)
res = []
for i in range(1, 10):
dfs(i)
return res岛屿问题
200. 岛屿数量
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3class Solution:
def numIslands(self, grid: List[List[str]]) -> int:
m,n = len(grid), len(grid[0])
def dfs(grid,i,j):
if not 0<=i695. 岛屿的最大面积
0 。class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
m,n = len(grid), len(grid[0])
def dfs(grid, i, j):
if not 0<=i463. 岛屿的周长
class Solution:
def islandPerimeter(self, grid: List[List[int]]) -> int:
m,n = len(grid), len(grid[0])
def dfs(grid, i, j):
if not 0<=i组合总和系列
39. 组合总和
输入:candidates = [2,3,6,7], target = 7
所求解集为:
[
[7],
[2,2,3]
]class Solution:
def combinationSum(self, candidates: List[int], target: int):
res = []
def dfs(cur, tmp, index): # 当前之和,当前列表,当前在candidates的第几个数
if cur==target:
res.append(tmp)
return
if cur>target:
return
for i in range(index, len(candidates)): # 从前往后遍历
dfs(cur+candidates[i], tmp + [candidates[i]], i) #可以重复选择数,因此仍为i
dfs(0, [], 0)
return res40. 组合总和 II
candidates 中的每个数字在每个组合中只能使用一次。class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort()
res = []
def dfs(cur, tmp, ind):
if cur==target:
res.append(tmp)
return
if cur>target:
return
for i in range(ind, len(candidates)):
if i>ind and candidates[i]==candidates[i-1]:
continue
dfs(cur+candidates[i], tmp+[candidates[i]], i+1) # i+1
dfs(0, [], 0)
return res跳跃系列
55. 跳跃游戏
nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个下标。class Solution:
def canJump(self, nums: List[int]) -> bool:
n = len(nums)
rightmost = 0
for i in range(n):
if i<=rightmost:
rightmost = max(rightmost, i+nums[i]) # 实时维护能够到达的最右侧距离
if rightmost>=n-1:
return True
return False45. 跳跃游戏 II
class Solution:
def jump(self, nums: List[int]) -> int:
n = len(nums)
maxpos, end, step = 0,0,0
for i in range(n-1):
maxpos = max(nums[i]+i, maxpos)
if i==end:
end = maxpos
step += 1
return step跳跃变体
我们新增加了一个变量 last_end,该变量用于存放上一个边界。如果遍历结束后,上一个边界为数组最后位置,说明其实上一步就已经到达了数组的最后位置,平白无故多跳了一步,因此返回 step-1,否则返回 step。def canJump(self, nums: List[int]) -> bool:
n = len(nums)
last_end = 0
maxPos, end, step = 0, 0, 0
for i in range(n):
if maxPos >= i:
maxPos = max(maxPos, i + nums[i])
if i == end:
last_end = end
end = maxPos
step += 1
else:
break
else:
if last_end == n-1:
return step-1
else:
return step
return False1306. 跳跃游戏 III
股票系列
121. 买卖股票的最佳时机
prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n<2:
return 0
pro = 0
m = float('inf')
for i in prices:
m = min(m, i)
pro = max(pro, i-m)
return pro122. 买卖股票的最佳时机 II
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n<1:
return 0
dp = [[None, None] for _ in range(n)]
dp[0][0] = 0
dp[0][1] = -prices[0] # 两个初始化
for i in range(1,n):
dp[i][0] = max(dp[i-1][0] ,dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1] ,dp[i-1][0]-prices[i])
return dp[-1][0] # 返回最后一天且手上没有股票时的获利情况class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n<2:
return 0
tmp = 0
res = 0
for i in range(1,n):
tmp = prices[i]-prices[i-1]
if tmp > 0:
res += tmp
return res 123、买卖股票的最佳时机III
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n<1:
return 0
dp = [[[None,None] for _ in range(3)] for _ in range(n)]
for i in range(n):
dp[i][0][0] = 0
dp[i][0][1] = -float('inf')
for j in range(1,3): # i=0时
dp[0][j][0] = 0
dp[0][j][1] = -prices[0]
for i in range(1,n):
for j in range(1,3):
dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1]+prices[i])
dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i])
return dp[-1][-1][0] # 最后一天,操作了最多次之后,卖出得到的利润class Solution:
def maxProfit(self, prices: List[int]) -> int:
buy1 = buy2 = float('inf')
pro1 = pro2 = 0
for price in prices:
buy1 = min(buy1, price)
pro1 = max(pro1, price-buy1)
buy2 = min(buy2, price-pro1) # price-pro1 是用第一次的钱抵消了一部分第二次购买花费的钱
pro2 = max(pro2, price-buy2)
return pro2188、买卖股票的最佳时机IV
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
n = len(prices)
if k>n//2: # 等价于k=inf,与122题相同
tmp = 0
res = 0
for i in range(1,n):
tmp = prices[i]-prices[i-1]
if tmp>0:
res += tmp
return res
else:
dp = [[[None, None] for _ in range(k+1)] for _ in range(n)]
for i in range(n):
dp[i][0][0] = 0
dp[i][0][1] = -float('inf')
for j in range(1,k+1):
dp[0][j][0] = 0
dp[0][j][1] = -prices[0]
for i in range(1, n):
for j in range(1,k+1):
dp[i][j][0] = max(dp[i-1][j][0], dp[i-1][j][1] + prices[i])
dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0] - prices[i])
return dp[-1][-1][0]309、含冷冻期
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n<2:
return 0
dp = [[0]*2 for _ in range(n)]
dp[0][0] = 0
dp[0][1] = -prices[0]
dp[1][0] = max(dp[0][0], dp[0][1]+prices[1])
dp[1][1] = max(dp[0][1], dp[0][0]-prices[1])
for i in range(2,n):
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0]-prices[i]) # 因为有冷冻期,需要i-2,隔一天
return dp[-1][0]打家劫舍系列
478. 在圆内随机生成点
randPoint 。import random
class Solution:
def __init__(self, radius: float, x_center: float, y_center: float):
self.r = radius
self.x = x_center
self.y = y_center
def randPoint(self) -> List[float]:
while 1:
u = 2*random.random() - 1
v = 2*random.random() - 1
if u*u + v*v <= 1:
return [self.x+u*self.r, self.y+v*self.r]179. 最大数
nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。输入
nums = [10,2]
输出:"210"class Solution:
def largestNumber(self, nums: List[int]) -> str:
def cmp(x, y): # 此处相当于是做了降序(reverse=True)
if x+yclass Solution:
def largestNumber(self, nums: List[int]) -> str:
strs = [str(n) for n in nums]
def quicksort(l,r):
if l>r:
return
i,j = l, r
pivot = strs[i]
while i207. 课程表
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
indeg = [0]*numCourses # 入度
edges = collections.defaultdict(list) #注意是数组
for info in prerequisites:
edges[info[1]].append(info[0])
indeg[info[0]] += 1
# print(edges)
# print(indeg)
q = collections.deque([u for u in range(numCourses) if indeg[u]==0]) # 入度为0的节点被放入队列中
visited = 0
while q:
visited += 1
u = q.popleft()
for v in edges[u]:
indeg[v] -= 1 # 移除u的所有出边
if indeg[v]==0: # 若某个节点的入度变为0,则放入队列中
q.append(v)
return visited==numCourses210. 课程表 II
输出: [0,1,2,3] or [0,2,1,3]
解释: 总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。class Solution:
def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
edges = collections.defaultdict(list)
indeg = [0]*numCourses
res = []
for info in prerequisites:
edges[info[1]].append(info[0])
indeg[info[0]] += 1
q = collections.deque([u for u in range(numCourses) if indeg[u]==0])
visited = 0
while q:
visited += 1
node = q.popleft()
res.append(node)
for v in edges[node]:
indeg[v] -= 1
if indeg[v]==0:
q.append(v)
if visited==numCourses:
return res
else:
return []栈
84. 柱状图中最大的矩形
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
stack = []
heights = [0] + heights + [0]
res = 0
for i in range(len(heights)):
while stack and heights[stack[-1]]>heights[i]:
tmp = stack.pop() # i是出栈元素tmp的右边第一个比其小的元素
res = max(res, heights[tmp]*(i - stack[-1]-1)) # 此时的stack[-1]是出栈元素tmp左边第一个比其小的元素, 减1是因为弹出了一个数
stack.append(i)
return res85. 最大矩形
0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。class Solution:
def maximalRectangle(self, matrix: List[List[str]]) -> int:
def maxarea(heights): # 84题,单调增栈计算最大矩形
heights = [0]+heights+[0]
stack = []
res = 0
for i in range(len(heights)):
while stack and heights[i]221. 最大正方形
'0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
m,n = len(matrix), len(matrix[0])
if m==0 or n==0:
return 0
dp = [[0]*n for _ in range(m)]
maxside = 0
for i in range(m):
for j in range(n):
if matrix[i][j]=='0':
dp[i][j] = 0
else:
if i==0 or j==0: # 处于边角时,正方形大小只能是1
dp[i][j] = 1
else:
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
maxside = max(maxside, dp[i][j])
res = maxside*maxside
return res456. 132 模式
class Solution:
def find132pattern(self, nums: List[int]) -> bool:
n = len(nums)
nums1 = [float('inf')]*(n)
for i in range(1, n):
nums1[i] = min(nums1[i-1], nums[i-1])
s = []
for j in range(n-1, -1, -1):
numsk = float('-inf')
while s and s[-1]496. 下一个更大元素 I
nums1 和 nums2 ,其中nums1 是 nums2 的子集。
输出: [3,-1]
解释:
对于 num1 中的数字 2 ,第二个数组中的下一个较大数字是 3 。
对于 num1 中的数字 4 ,第二个数组中没有下一个更大的数字,因此输出 -1 。O(nums1.length + nums2.length) 的解决方案吗?class Solution:
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
n1, n2 = len(nums1), len(nums2)
right = []
dic = {}
for i in range(n2):
while right and right[-1]88. 合并两个有序数组
class Solution:
def merge(self, A: List[int], m: int, B: List[int], n: int) -> None:
"""
Do not return anything, modify A in-place instead.
"""
i,j = m-1, n-1
k = m+n-1
while i>=0 and j>=0:
if A[i]剑指 Offer 51. 数组中的逆序对
class Solution:
def reversePairs(self, nums: List[int]) -> int:
def merge(l,r):
if l>=r:
return 0
mid = (l+r)//2
res = merge(l, mid) + merge(mid+1, r) #递归划分
i,j = l, mid+1
tmp[l:r+1] = nums[l:r+1]
for k in range(l, r+1):
if i==mid+1: # 左侧已经完成,直接添加右侧数组的数字
nums[k] = tmp[j]
j += 1
elif j==r+1 or tmp[i]<=tmp[j]:
nums[k] = tmp[i]
i += 1
else:
nums[k] = tmp[j]
j +=1
res += mid -i+1 #左子数组当前元素到末尾元素的个数
return res
tmp = [0]*len(nums)
return merge(0, len(nums)-1)295. 数据流的中位数
double findMedian() - 返回目前所有元素的中位数。import heapq
class MedianFinder:
def __init__(self):
"""
initialize your data structure here.
"""
self.min_heap = []
self.max_heap = []
self.count = 0 # 当前大顶堆和小顶堆的元素个数之和
def addNum(self, num: int) -> None:
self.count += 1
heapq.heappush(self.max_heap, (-num, num))
# 因为 Python 中的堆默认是小顶堆,所以要传入一个 tuple,用于比较的元素需是相反数,
# 才能模拟出大顶堆的效果
_, max_heap_top = heapq.heappop(self.max_heap)
heapq.heappush(self.min_heap, max_heap_top)
if self.count&1==1: # 如果是奇数,就将最小堆堆顶的元素拿给最大堆。
min_heap_top = heapq.heappop(self.min_heap)
heapq.heappush(self.max_heap, (-min_heap_top, min_heap_top))
def findMedian(self) -> float:
if self.count&1==1: # 奇数
return self.max_heap[0][1] #最后取得正数
else:
return (self.max_heap[0][1]+self.min_heap[0])/2483. 最小好进制
class Solution:
def smallestGoodBase(self, n: str) -> str:
num = int(n)
for m in range(num.bit_length(), 2, -1):
x = int(pow(num, 1/(m-1)))
if num==(pow(x,m)-1)//(x-1): # 等比数列求和 n = (x^m - 1)/(x-1)
return str(x)
return str(num-1)字符串
3. 无重复字符的最长子串
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是
"abc",所以其长度为 3。class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
queue = []
length = [] # 保存不含重复字符的子串长度
for char in s:
if char not in queue:
queue.append(char)
else: # 若字符在queue中
length.append(len(queue))
while queue[0]!=char:
queue.pop(0) # 不断pop出元素
queue.pop(0)
queue.append(char)
length.append(len(queue))
return max(length)76. 最小覆盖子串
s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。class Solution:
def minWindow(self, s: str, t: str) -> str:
need = collections.defaultdict(int)
for c in t:
need[c] += 1
left, right = 0,0
n = len(s)
count = len(t)
min_len = float('inf')
res = ''
while right面试题 17.18. 最短超串
class Solution:
def shortestSeq(self, big: List[int], small: List[int]) -> List[int]:
need = collections.defaultdict(int)
res = 0 # 保存左端点
for c in small:
need[c]+=1
left, right =0,0
min_len = float('inf')
count = len(small)
while right5. 最长回文子串
s,找到 s 中最长的回文子串。class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
if n<2:
return s
max_len = 0
for i in range(n):
left, right = i, i
while left>1 and s[left-1]==s[i]: # 左侧元素和中心元素相同
left -=1
while right647. 回文子串
class Solution:
def countSubstrings(self, s: str) -> int:
count = 0
n = len(s)
dp = [[False]*n for _ in range(n)]
for j in range(n):
for i in range(j+1):
length = j-i+1
if length==1:
dp[i][j]=True
count += 1
if length==2 and s[i]==s[j]:
dp[i][j] = True
count += 1
if length>2 and s[i]==s[j] and dp[i+1][j-1] is True: #除了首尾,其他仍为回文子串
dp[i][j] = True
count += 1
return count14. 最长公共前缀
""。class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
if not strs:
return ''
strs.sort() # 排序
s1 = strs[0]
n = len(strs)
for i in range(1, n):
s1 = self.f(s1, strs[i])
if not s1:
break
return s1
def f(self, s1, s2):
length, ind = min(len(s1), len(s2)), 0
while ind20. 有效的括号
'(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。class Solution:
def isValid(self, s: str) -> bool:
pairs = {')':'(',']':'[','}' :'{'}
if len(s)&1!=0: # 个数为奇数,无效
return False
res = []
for ch in s:
if ch in pairs:
if not res or res[-1]!=pairs[ch]: # 先判断是否为空,若为空(例如输入是"]{")则直接返回false
return False
res.pop()
else:
res.append(ch)
if not res: # 最后看栈中是否为空
return True
else:
return False678. 有效的括号字符串
任何右括号 ) 必须有相应的左括号 ( 。
左括号 ( 必须在对应的右括号之前 )。
* 可以被视为单个右括号 ) ,或单个左括号 ( ,或一个空字符串。
一个空字符串也被视为有效字符串。22. 括号生成
n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 有效括号组合需满足:左括号必须以正确的顺序闭合。class Solution:
def generateParenthesis(self, n: int) -> List[str]:
res = []
def dfs(path, left, right):
if left>n or right>left:
return
if len(path)==2*n:
res.append(path)
return
dfs(path+'(', left+1, right)
dfs(path+')', left, right+1)
dfs('', 0, 0)
return res32. 最长有效括号
'(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
题解:
当 left 计数器与 right 计数器相等时,我们计算当前有效字符串的长度,并且记录目前为止找到的最长子字符串
这样我们就能涵盖所有情况从而求解出答案。class Solution:
def longestValidParentheses(self, s: str) -> int:
res = 0
left, right = 0, 0
n = len(s)
for i in range(n):
if s[i]=='(':
left += 1
else:
right += 1
if left==right:
res = max(res, 2*right)
elif right>left:
left = right = 0
left = right = 0
for i in range(n-1, -1, -1):
if s[i]=='(':
left += 1
else:
right += 1
if left==right:
res = max(res, 2*left)
elif left>right:
left = right = 0
return res72. 编辑距离
word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数。
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
n1, n2 = len(word1), len(word2)
dp = [[0]*(n2+1) for _ in range(n1+1)]
for i in range(1, n1+1):
dp[i][0] = dp[i-1][0] + 1
for j in range(1, n2+1):
dp[0][j] = dp[0][j-1] + 1
for i in range(1, n1+1):
for j in range(1, n2+1):
if word1[i-1]==word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1])+1
return dp[-1][-1]165. 比较版本号
'.' 连接。每个修订号由 多位数字 组成,可能包含 前导零 。
version1 > version2 返回 1,version1 < version2 返回 -1,0。class Solution:
def compareVersion(self, version1: str, version2: str) -> int:
v1 = [int(i) for i in version1.split('.')]
v2 = [int(j) for j in version2.split('.')]
v1_len = len(v1)
v2_len = len(v2)
maxlen = max(v1_len, v2_len) # 对短的进行补零
v1 = v1 + [0]*(maxlen - v1_len)
v2 = v2 + [0]*(maxlen - v2_len)
if v1>v2:
return 1
elif v1面试题 01.06. 字符串压缩
class Solution:
def compressString(self, S: str) -> str:
if not S:
return S
n = len(S)
tmp = S[0]
res = tmp
count = 1
for i in range(1, n):
if S[i]==tmp:
count += 1
else:
tmp = S[i]
res = res + str(count)+ str(tmp)
count = 1
res = res+str(count)
if len(res)115. 不同的子序列
class Solution:
def numDistinct(self, s: str, t: str) -> int:
s1,t1 = len(s), len(t)
if s128. 实现 strStr()
class Solution:
def strStr(self, a, b):
n1,n2 = len(a), len(b)
if n2==0:
return 0
if n1class Solution:
def strStr(self, a, b):
n,m = len(a), len(b)
if m==0:
return 0
next = self.getnext(m, b)
print(next)
p = -1
for j in range(n):
while p>=0 and b[p+1]!=a[j]:
p = next[p]
if b[p+1]==a[j]:
p += 1
if p==m-1: # 到达最后
return j-m+1
return -1
def getnext(self, m, b): # 构建next数组
next = ['' for i in range(m)]
k = -1
next[0] = k
for i in range(1, m):
while (k>-1 and b[k+1]!=b[i]): # 不匹配
k = next[k] # 寻找之前匹配的位置
if b[k+1]==b[i]: #匹配,i,k同时向后移动
k += 1
next[i] = k
return next
131. 分割回文串
s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]class Solution:
def partition(self, s: str) -> List[List[str]]:
if len(s)==1:
return [[s]]
res = []
path = [] # 已经是回文的子串
def traceback(index): # 下一轮递归遍历的起始下标
if index==len(s):
res.append(path[:])
return
for i in range(index, len(s)):
sub = s[index:i+1] # 截取的子串
if sub==sub[::-1]: # 是回文串,就直接加入到path中
path.append(sub)
else:
continue
traceback(i+1)
path.pop()
traceback(0)
return res93. 复原 IP 地址
class Solution:
def restoreIpAddresses(self, s: str) -> List[str]:
res = []
def traceback(tmp, index):
if len(tmp)>4:
return
if len(tmp)==4 and index==len(s):
res.append('.'.join(tmp[:]))
return
for i in range(index, len(s)):
if not 0<=int(s[index:i+1])<=255:
continue
#如果当前值是0,但是不是一个单"0"则剪掉
if int(s[index : i+ 1]) == 0 and i != index:
continue
if int(s[index:i+ 1]) > 0 and s[index] == "0":#如果当前值不是0,但是却以"0XXX"开头,也应该剪掉
continue
tmp.append(s[index:i+1])
traceback(tmp, i+1)
tmp.pop()
traceback([], 0)
return res91. 解码方法
'B' -> 2
...
'Z' -> 26
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。s ,请计算并返回 解码 方法的 总数 。class Solution:
def numDecodings(self, s: str) -> int:
n = len(s)
dp = [1]+[0]*n
for i in range(1, n+1):
if s[i-1]!='0':
dp[i] += dp[i-1]
if i>=2 and s[i-2]!='0' and int(s[i-2:i])<=26:
dp[i] += dp[i-2]
return dp[-1]524. 通过删除字母匹配到字典里最长单词
class Solution:
def findLongestWord(self, s: str, dictionary: List[str]) -> str:
res = ''
length = 0
for d in dictionary:
i,j = 0,0
while i97. 交错字符串
s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出:trueclass Solution:
def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
m,n = len(s1), len(s2)
if (m+n)!=len(s3):
return False
dp = [[0]*(n+1) for _ in range(m+1)]
dp[0][0] = 1
for i in range(1, m+1):
dp[i][0] = dp[i-1][0] and s1[i-1]==s3[i-1]
for j in range(1, n+1):
dp[0][j] = dp[0][j-1] and s2[j-1]==s3[j-1]
for i in range(1,m+1):
for j in range(1,n+1):
dp[i][j] = (dp[i][j-1] and s2[j-1]==s3[i+j-1]) or (dp[i-1][j] and s1[i-1]==s3[i+j-1])
return dp[-1][-1]==130. 串联所有单词的子串
class Solution:
def findSubstring(self, s: str, words: List[str]) -> List[int]:
if not s or len(s)==0 or not words or len(words)==0:
return []
n = len(s)
m = len(words[0])
words_map = dict() # 将每个单词以及出现的频率记录到字典中
for i in words:
if i not in words_map:
words_map[i] = 1
else:
words_map[i] += 1
all_words = m*len(words)
res = []
for i in range(n-all_words+1): # 每次取 all_words长度的子串
tmp, d = s[i:i+all_words], dict(words_map)
for j in range(0, len(tmp), m):
# 从子串tmp中取出one_word_size长度的子串,看是否出现在临时字典中
# 如果是就将临时字典记录的频率-1,如果不在就跳出循环
key = tmp[j:j+m]
if key in d:
d[key] -= 1
if d[key]==0:
del d[key]
else:
break
if not d:
res.append(i)
return res