卡尔曼滤波(Kalman Filter)

卡尔曼滤波(Kalman Filter)

微信公众号：幼儿园的学霸
个人的学习笔记，关于OpenCV,关于机器学习, …。问题或建议，请公众号留言;

目录

[TOC]

what is Kalman Filter

举个例子，对于雷达来说，我们感兴趣的是其能够跟踪目标，但对目标的位置、速度、加速度的测量值往往存在噪声。卡尔曼滤波利用目标的动态信息，设法去掉噪声的影像，得到一个关于目标位置的好的估计。这个估计可以是对当前目标位置的估计(滤波)，也可以是对于将来位置的估计（预测），也可以是对过去位置的估计（插值或者平滑）。

卡尔曼滤波器的两个重要假设

1.被建模的系统是线性的：K时刻的系统状态可以用某个矩阵与K-1时刻的系统状态的乘积表示；
2.影像测量的噪声属于高斯分布的白噪声（White Gaussian Noise）：噪声与时间不相关，且只用均值和协方差就可以准确地为幅值建模（也就是噪声完全由一阶矩和二阶距描述）。

卡尔曼滤波理论回顾

首先对于离散控制系统，其系统状态和系统测量值可进行以下表示：

X(k) = A*X(k-1) + B*U(k) + W(k)    

Z(k) = H*X(k) + V(k)     

X(k):系统k时刻状态
A：状态转移矩阵，对应opencv里kalman滤波器的transitionMatrix矩阵（关于opencv kalman滤波器详细定义会在2中给出）
B：控制输入矩阵，对应opencv里kalman滤波器的controlMatrix矩阵
U(k)：k时刻对系统的控制量
Z(k)： k时刻的测量值
H：系统测量矩阵，对应opencv里kalman滤波器的measurementMatrix矩阵
W(k)：系统过程噪声，为高斯白噪声，协方差为Q，对应opencv里的kalman滤波器的processNoiseCov矩阵
V(k)： 测量噪声，也为高斯白噪声，协方差为R，对应opencv里的kalman滤波器的measurementNoiseCov矩阵

对于满足上面的条件(线性随机微分系统，过程和测量都是高斯白噪声)，卡尔曼滤波器是最优的信息处理器。
接下来便是核心的5个公式。

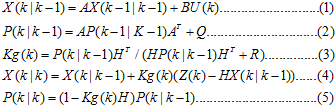
这5个式子可分成3部分看。
第一部分：
式(1)-(2)：预测值的计算
式(1)：计算基于k-1时刻状态对k时刻系统状态的预测值
X(k|k-1)：基于k-1时刻状态对k时刻状态的预测值，对应opencv里kalman滤波器的predict()输出，即statePre矩阵
X(k-1|k-1)：k-1时刻状态的最优结果，对应opencv里kalman滤波器的上一次状态的statePost矩阵
U(k)： k时刻的系统控制量，无则为0
A： 状态转移矩阵，对应opencv里kalman滤波器的transitionMatrix矩阵
B： 控制输入矩阵，对应opencv里kalman滤波器的controlMatrix矩阵
式(2)：计算X(k|k-1)对应的协方差的预测值
P(k|k-1)： 基于k-1时刻的协方差计算k时刻协方差的预测值，对应opencv里kalman滤波器的errorCovPre矩阵
P(k-1|k-1)：k-1时刻协方差的最优结果，对应opencv里kalman滤波器的上一次状态的errorCovPost矩阵
Q： 系统过程噪声协方差，对应opencv里kalman滤波器的processNoiseCov矩阵
第二部分：
式(3):增益的计算
Kg(k)：k时刻的kalman增益，为估计量的方差占总方差(估计量方差和测量方差)的比重，对应opencv里kalman滤波器的gain矩阵
H：系统测量矩阵，对应opencv里kalman滤波器的measurementMatrix矩阵
R：测量噪声协方差，对应opencv里的kalman滤波器的measurementNoiseCov矩阵
第三部分：
式(4)--(5):k时刻的更新
式(4)：计算k时刻系统状态最优值
X(k|k)：k时刻系统状态的最优结果，对应opencv里kalman滤波器的k时刻状态的statePost矩阵
Z(k)：k时刻系统测量值
式(5)：计算k时刻系统最优结果对应的协方差
P(k|k)：k时刻系统最优结果对应的协方差，对应opencv里kalman滤波器的errorCovPost矩阵

以上便是Kalman的核心部分
运行(1)(2)-(3)-(4)(5)-(1)(2)…
输出即为X(k|k)，k时刻系统状态最优估计值.
运行流程见下图所示

OpenCV中的KalmanFilter详解

KalmanFilter类注释说明

OpenCV中有两个版本的卡尔曼滤波方法KalmanFilter(C++)和CvKalman©，用法差不太多，这里只介绍KalmanFilter。

C++版本中将KalmanFilter封装到一个类中，其结构如下所示：

class CV_EXPORTS_W KalmanFilter
{
public:    
    CV_WRAP KalmanFilter(); //构造默认KalmanFilter对象
    CV_WRAP KalmanFilter(int dynamParams, //状态的维数
        int measureParams, //测量的维数
        int controlParams=0, //控制量的维数
        int type=CV_32F//创建矩阵类型（CV_32F or CV_64F）
        ); //完整构造KalmanFilter对象方法
    void init(int dynamParams, int measureParams, int controlParams=0, int type=CV_32F); //初始化KalmanFilter对象，会替换原来的KF对象
  
    CV_WRAP const Mat& predict(const Mat& control=Mat()); //计算预测的状态值    
    CV_WRAP const Mat& correct(const Mat& measurement); //根据测量值更新状态值
 
    Mat statePre;            //预测值 (x'(k)): x(k)=A*x(k-1)+B*u(k)
    Mat statePost;           //状态值 (x(k)): x(k)=x'(k)+K(k)*(z(k)-H*x'(k))
    Mat transitionMatrix;    //状态转移矩阵 A
    Mat controlMatrix;       //控制矩阵 B 
    Mat measurementMatrix;   //测量矩阵 H
    Mat processNoiseCov;     //系统误差 Q
    Mat measurementNoiseCov; //测量误差 R
    Mat errorCovPre;         //最小均方误差 (P'(k)): P'(k)=A*P(k-1)*At + Q)
    Mat gain;                //卡尔曼增益   (K(k)): K(k)=P'(k)*Ht*inv(H*P'(k)*Ht+R)
    Mat errorCovPost;        //修正的最小均方误差 (P(k)): P(k)=(I-K(k)*H)*P'(k)
 
    // 临时矩阵
    Mat temp1;
    Mat temp2;
    Mat temp3;
    Mat temp4;
    Mat temp5;
};
 
enum
{
    OPTFLOW_USE_INITIAL_FLOW = CV_LKFLOW_INITIAL_GUESSES,
    OPTFLOW_LK_GET_MIN_EIGENVALS = CV_LKFLOW_GET_MIN_EIGENVALS,
    OPTFLOW_FARNEBACK_GAUSSIAN = 256
};

只有四个方法:

• 构造KF对象KalmanFilter(DP,MP,CP)
• 初始化KF对象init(DP,MP,CP)
• 预测predict( )
• 更新correct( )。

除非你要重新构造KF对象，否则用不到init( )。而KalmanFilter(DP,MP,CP)和init( )就是赋值，用来构造或者初始化KF对象。
注意：KalmanFilter结构体中并没有测量值，测量值需要自己定义，而且一定要定义，因为后面要用。

KalmanFilter编程步骤

• step1：定义KalmanFilter类并初始化

//构造KF对象
KalmanFilter KF(DP, MP, 0);

//初始化相关参数
KF.transitionMatrix //转移矩阵 A
KF.measurementMatrix //测量矩阵 H
KF.processNoiseCov//过程噪声 Q
KF.measurementNoiseCov//测量噪声 R
KF.errorCovPost//最小均方误差 P
KF.statePost//系统初始状态 x(0)
Mat measurement//定义初始测量值 z(0)

• step2：预测

KF.predict( ) //返回的是下一时刻的状态值KF.statePost (k+1)

• step3：更新

//更新measurement;
//注意measurement不能通过观测方程进行计算得到，要自己定义！

//更新KF
KF.correct(measurement)

//最终的结果应该是更新后的statePost.

相关参数的确定

对于系统状态方程，简记为Y=AX+B，X和Y是表示系统状态的列向量，A是转移矩阵，B是其他项。
状态值（向量）只要能表示系统的状态即可，状态值的维数决定了转移矩阵A的维数，比如X和Y是NX1的，则A是NXN的。
A的确定跟X有关，只要保证方程中不相干项的系数为0即可，看下面例子

• X和Y是二维的，

$$\left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\ast \left[\begin{array}{c}x\\ y\end{array}\right]+B$$

对于二维的变量，我看到用法比较多的是如下这种形式的(可以这样理解：x’ = x+dx)：

为什么状态值一般都设置成（x,y,△x,△y）？我们不妨设置成(x,y,△x)，对应的转移矩阵也改成3×3的。可以看到仍能跟上，不过在x方向跟踪速度快，在y方向跟踪速度慢。进一步设置成(x,y)和2×2的转移矩阵，程序的跟踪速度简直是龟速。所以，简单理解，△x和△y严重影响对应方向上的跟踪速度。

$$\left[\begin{array}{c}{x}^{-}\\ y^{-}\\ dx\\ dy\end{array}\right]=\left[\begin{array}{cccc}1& 0& 1& 0\\ 0& 1& 0& 1\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ dx\\ dy\end{array}\right]+B$$

• x、y、z是三维的

$$\left[\begin{array}{c}x\\ y\\ z\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ z\end{array}\right]+B$$

• x、y是三维的，但x和dx是相关项，此时按照矩阵元素排列形式，有如下两种形式

$$\left[\begin{array}{c}x\\ y\\ dx\end{array}\right]=\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}x\\ y\\ dx\end{array}\right]+B$$

$$\left[\begin{array}{c}x\\ dx\\ y\end{array}\right]=\left[\begin{array}{ccc}1& 1& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]\ast \left[\begin{array}{c}x\\ dx\\ y\end{array}\right]+B$$
即：X1=X+dX，依次类推。所以这个矩阵还是很容易却确定的，可以根据自己的实际情况定制转移矩阵。
当然上面转移矩阵中并不一定得是1和0，也可以是其他值。

OpenCVKalmanFilter编程示例

点的圆周运动预测

//====================================================================//
// Created by liheng on 19-2-26.
//Program:OpenCV自带的卡尔曼滤波器示例
//Data:2019.2.26
//Author:liheng
//Version:V1.0
//====================================================================//

#include 
#include 
#include 
#include 
#include 
using namespace std;
using namespace cv;

//计算相对窗口的坐标值，因为坐标原点在左上角，所以sin前有个负号
static inline Point calcPoint(Point2f center, double R, double angle)
{
    return center + Point2f((float)cos(angle), (float)-sin(angle))*(float)R;
}

static void help()
{
    printf( "\nExamle of c calls to OpenCV's Kalman filter.\n"
            "   Tracking of rotating point.\n"
            "   Rotation speed is constant.\n"
            "   Both state and measurements vectors are 1D (a point angle),\n"
            "   Measurement is the real point angle + gaussian noise.\n"
            "   The real and the estimated points are connected with yellow line segment,\n"
            "   the real and the measured points are connected with red line segment.\n"
            "   (if Kalman filter works correctly,\n"
            "    the yellow segment should be shorter than the red one).\n"
            "\n"
            "   Pressing any key (except ESC) will reset the tracking with a different speed.\n"
            "   Pressing ESC will stop the program.\n"
    );
}

int main(int, char**)
{
    help();
    Mat img(500, 500, CV_8UC3);
    KalmanFilter KF(2, 1, 0); //创建卡尔曼滤波器对象KF.虽然这个点是在2维平面中运动，但由于它是在一个圆弧上运动，只有一个自由度，角度，所以还是1维的
    Mat state(2, 1, CV_32F); //state(角度，△角度)
    Mat processNoise(2, 1, CV_32F);
    Mat measurement = Mat::zeros(1, 1, CV_32F);//定义测量值
    char code = (char)-1;

    for(;;)
    {
        //1.初始化
        cv::randn( state, Scalar::all(0), Scalar::all(0.1) );//填充高斯分布随机数
        KF.transitionMatrix = (Mat_(2, 2) << 1, 1, 0, 1);  //转移矩阵A[1,1;0,1]


        //将下面几个矩阵设置为对角阵
        //cv::setIdentity()函数--将矩阵的对角线元素设为指定值，其他元素为0
        cv::setIdentity(KF.measurementMatrix);                             //测量矩阵H
        cv::setIdentity(KF.processNoiseCov, Scalar::all(1e-5));            //系统噪声方差矩阵Q,//过程噪声协方差矩阵，标准差为1e-5
        cv::setIdentity(KF.measurementNoiseCov, Scalar::all(1e-1));        //测量噪声方差矩阵R,//测量噪声协方差矩阵R，标准差为1e-1
        cv::setIdentity(KF.errorCovPost, Scalar::all(1));                  //后验错误估计协方差矩阵P//P(1|1),估计协方差矩阵

        cv::randn(KF.statePost, Scalar::all(0), Scalar::all(0.1));          //x(0)初始化

        for(;;)
        {
            Point2f center(img.cols*0.5f, img.rows*0.5f);          //center图像中心点
            float R = img.cols/3.f;                                //半径
            double stateAngle = state.at(0);                //跟踪点角度
            Point statePt = calcPoint(center, R, stateAngle);     //跟踪点坐标statePt

            //2. 预测
            Mat prediction = KF.predict();                       //计算预测值，返回x'
            double predictAngle = prediction.at(0);          //预测点的角度
            Point predictPt = calcPoint(center, R, predictAngle);   //预测点坐标predictPt


            //3.更新
            //measurement是测量值
            randn( measurement, Scalar::all(0), Scalar::all(KF.measurementNoiseCov.at(0)));     //给measurement赋值N(0,R)的随机值

            // generate measurement
            measurement += KF.measurementMatrix*state;  //z = z + H*x;

            double measAngle = measurement.at(0);
            Point measPt = calcPoint(center, R, measAngle);

            // plot points
            //定义了画十字的方法，值得学习下
#define drawCross( center, color, d )                                 \
                line( img, Point( center.x - d, center.y - d ),                \
                             Point( center.x + d, center.y + d ), color, 1, CV_AA, 0); \
                line( img, Point( center.x + d, center.y - d ),                \
                             Point( center.x - d, center.y + d ), color, 1, CV_AA, 0 )

            img = Scalar::all(0);
            drawCross( statePt, Scalar(255,255,255), 3 );
            drawCross( measPt, Scalar(0,0,255), 3 );
            drawCross( predictPt, Scalar(0,255,0), 3 );
            line( img, statePt, measPt, Scalar(0,0,255), 3, CV_AA, 0 );
            line( img, statePt, predictPt, Scalar(0,255,255), 3, CV_AA, 0 );


            //调用kalman这个类的correct方法得到加入观察值校正后的状态变量值矩阵
            if(theRNG().uniform(0,4) != 0)
                KF.correct(measurement);

            //不加噪声的话就是匀速圆周运动，加了点噪声类似匀速圆周运动，因为噪声的原因，运动方向可能会改变
            randn( processNoise, Scalar(0), Scalar::all(sqrt(KF.processNoiseCov.at(0, 0))));   //vk
            state = KF.transitionMatrix*state + processNoise;

            imshow( "Kalman", img );
            code = (char)waitKey(100);

            if( code > 0 )
                break;
        }
        if( code == 27 || code == 'q' || code == 'Q' )
            break;
    }

    return 0;
}

鼠标位置的预测

//====================================================================//
// Created by liheng on 19-2-28.
//Program:卡尔曼滤波器示例2--跟踪鼠标位置
//Data:2019.2.28
//Author:liheng
//Version:V1.0
//====================================================================//


#include "opencv2/video/tracking.hpp"
#include "opencv2/highgui/highgui.hpp"
#include 
using namespace cv;
using namespace std;

const int winHeight=600;
const int winWidth=800;


Point mousePosition= Point(winWidth>>1,winHeight>>1);

//mouse event callback
void mouseEvent(int event, int x, int y, int flags, void *param )
{
    if (event==cv::EVENT_MOUSEMOVE) {
        mousePosition = Point(x,y);
    }
}

int main (void)
{
    RNG rng;
    //1.kalman filter setup
    const int stateNum=4;                                      //状态值4×1向量(x,y,△x,△y)//状态数，这里鼠标坐标X,Y和速度DX,DY
    const int measureNum=2;                                    //测量值2×1向量(x,y)//观测量数量，这里只写了X,Y
    KalmanFilter KF(stateNum, measureNum, 0);                   //第三个为控制量参数，这里没有

    KF.transitionMatrix = (Mat_(4, 4) <<1,0,1,0,0,1,0,1,0,0,1,0,0,0,0,1);  //转移矩阵A
    setIdentity(KF.measurementMatrix);                                             //测量矩阵H
    setIdentity(KF.processNoiseCov, Scalar::all(1e-5));                            //系统噪声方差矩阵Q
    setIdentity(KF.measurementNoiseCov, Scalar::all(1e-1));                        //测量噪声方差矩阵R
    setIdentity(KF.errorCovPost, Scalar::all(1));                                  //后验错误估计协方差矩阵P
    rng.fill(KF.statePost,RNG::UNIFORM,0,winHeight>winWidth?winWidth:winHeight);   //初始状态值x(0)
    Mat measurement = Mat::zeros(measureNum, 1, CV_32F);                           //初始测量值x'(0)，因为后面要更新这个值，所以必须先定义

    namedWindow("kalman");
    setMouseCallback("kalman",mouseEvent);

    Mat image(winHeight,winWidth,CV_8UC3,Scalar(0));

    while (1)
    {
        //2.kalman prediction
        Mat prediction = KF.predict();
        Point predict_pt = Point(prediction.at(0),prediction.at(1) );   //预测值(x',y')

        //3.update measurement
        measurement.at(0) = (float)mousePosition.x;
        measurement.at(1) = (float)mousePosition.y;

        //4.update
        KF.correct(measurement);

        //最优值
        Point statePt = Point(KF.statePost.at(0),KF.statePost.at(1));

        //draw
        image.setTo(Scalar(255,255,255,0));
        circle(image,predict_pt,5,Scalar(0,255,0),3);    //predicted point with green
        circle(image,mousePosition,5,Scalar(255,0,0),3); //current position with red
        circle(image,statePt,5,Scalar(0,255,255),3); //current position with yellow

        char buf[256];
        sprintf(buf,"predicted position:(%3d,%3d)",predict_pt.x,predict_pt.y);
        putText(image,buf,cv::Point(10,30),cv::FONT_HERSHEY_SCRIPT_COMPLEX,1,Scalar(0,0,0),1,8);

        sprintf(buf,"current position :(%3d,%3d)",mousePosition.x,mousePosition.y);
        putText(image,buf,cv::Point(10,60),cv::FONT_HERSHEY_SCRIPT_COMPLEX,1,Scalar(0,0,0),1,8);

        sprintf(buf,"best position:(%3d,%3d)",statePt.x,statePt.y);
        putText(image,buf,cv::Point(10,90),cv::FONT_HERSHEY_SCRIPT_COMPLEX,1,Scalar(0,0,0),1,8);

        imshow("kalman", image);
        int key=waitKey(3);
        if (key==27){//esc
            break;
        }
    }
}

运行结果如图所示：

卡尔曼滤波器的不足之处

1.滤波限制条件比较苛刻，它要求系统模型精确以及系统误差模型和观测误差模型已知，这在实际应用中是很难满足的，或者在系统工作过程中，模型发生变化，这些都导致传统KF的滤波发散或精度下降。
2.计算机字长的限制，这种情况可能导致计算过程中出现舍入误差，从而导致方差阵P ( k | k)不对称引起滤波发散。
3.观测数据发生突变，由于传感器故障或外部条件发生改变，极有可能出现数据突变，即野值，这会对滤波器的收敛性产生严重影响，甚至导致发散，可以说，野值是对滤波器稳定性的一个考验。

卡尔曼滤波的发展

针对上述不足，很多学者提出了不同的方法加以克服，如限定记忆法、平方根滤波、渐消记忆滤波、自适应卡尔曼滤波（AKF）、抗野值滤波等。其中，AKF因为具有自适应特性非常适合动态系统滤波而受到广泛重视。因此，在采用卡尔曼滤波处理动态测量数据时，一般都要考虑采取适当的自适应滤波方法来解决这一问题。

---

下面的是我的公众号二维码图片，欢迎关注。