旋转矩阵和欧拉角

欧拉角介绍

旋转可以参考两种坐标系,内部坐标系(XYZ), 角度 α, β, γ.
外部坐标系(xyz), 角度 ψ, θ, φ.
不考虑参考坐标系情况下, 按照旋转方式可以分为两种:

• Proper Euler angles
  (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)

• Tait–Bryan angles
  (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z).
  与proper方式相比, Tait方式旋转会用上所有坐标轴.
  我们常说的欧拉角指的都是Tait-Bryan angles.

• 旋转矩阵与欧拉角转换参考Computing Euler angles from a rotation matrix
  
  维基百科给的公式:
  

• 旋转矩阵转换为欧拉角(Tait-Bryan angles)参考代码

#Ref: https://www.learnopencv.com/rotation-matrix-to-euler-angles/
def isRotationMatrix(R):
    ''' checks if a matrix is a valid rotation matrix(whether orthogonal or not)
    '''
    Rt = np.transpose(R)
    shouldBeIdentity = np.dot(Rt, R)
    I = np.identity(3, dtype = R.dtype)
    n = np.linalg.norm(I - shouldBeIdentity)
    return n < 1e-6

def matrix2angle(R):
    ''' get three Euler angles from Rotation Matrix
    Args:
        R: (3,3). rotation matrix
    Returns:
        x: pitch
        y: yaw
        z: roll
    '''
    assert(isRotationMatrix)
    sy = math.sqrt(R[0,0] * R[0,0] +  R[1,0] * R[1,0])
     
    singular = sy < 1e-6
 
    if  not singular :
        x = math.atan2(R[2,1] , R[2,2])
        y = math.atan2(-R[2,0], sy)
        z = math.atan2(R[1,0], R[0,0])
    else :
        x = math.atan2(-R[1,2], R[1,1])
        y = math.atan2(-R[2,0], sy)
        z = 0

    # rx, ry, rz = np.rad2deg(x), np.rad2deg(y), np.rad2deg(z)
    rx, ry, rz = x*180/np.pi, y*180/np.pi, z*180/np.pi
    return rx, ry, rz

参考:
rotations_in_3d_part1.html

坐标系旋转

首先坐标系的旋转和点的旋转是相反的. 这里先讨论下坐标系的旋转.
假设在xoy坐标系下有个点p, 那么这个点在sot坐标系下的坐标是多少呢?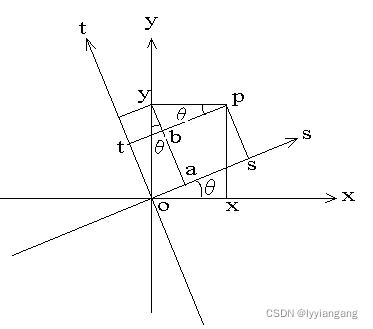
这里先假设xoy坐标系下点坐标为X,sot坐标系下点坐标为X’, 这里先假设他们应该有如下关系:$R{X}^{\prime }=X$,其中$R=[s,t]$ .
现在开始证明为什么R可以用s和t这么表示. 直观上可以知道, 如果$X^{\prime }=[1,0,0{]}^T$, 那么就可以取出R的第一列也就是$s$, 所以可以反推出R的表示形式.
从上图不难看出, $s=[cos(\theta ),sin(\theta ){]}^T$ , $t=[-sin(\theta ),cos(\theta ){]}^T$, 所以旋转矩阵表示为:
$$R=[s,t]=\left[\begin{array}{cc}cos(\theta )& -sin(\theta )\\ sin(\theta )& cos(\theta )\end{array}\right]$$
另一方面可以这么理解, 我们知道一个点是可以通过坐标系的基空间表示的.常见的表示方法:

对与sot坐标系则有:
$op=[ss,tt{]}^T$ , 而基向量st又是用xoy坐标系表示的, 所以, 矩阵$[s,t]$有了将sot坐标系点转到xoy坐标系点的能力.
opengl中有个lookat函数, 能够将世界坐标系的点转换为相机坐标系下,可以注意下里面的R.

def lookat_camera(vertices, eye, at = None, up = None):
    """ 'look at' transformation: from world space to camera space
    standard camera space: 
        camera located at the origin. 
        looking down negative z-axis. 
        vertical vector is y-axis.
    Xcam = R(X - C)
    Homo: [[R, -RC], [0, 1]]
    Args:
      vertices: [nver, 3] 
      eye: [3,] the XYZ world space position of the camera.
      at: [3,] a position along the center of the camera's gaze.
      up: [3,] up direction 
    Returns:
      transformed_vertices: [nver, 3]
    """
    if at is None:
      at = np.array([0, 0, 0], np.float32)
    if up is None:
      up = np.array([0, 1, 0], np.float32)

    eye = np.array(eye).astype(np.float32)
    at = np.array(at).astype(np.float32)
    z_aixs = -normalize(at - eye) # look forward
    x_aixs = normalize(np.cross(up, z_aixs)) # look right
    y_axis = np.cross(z_aixs, x_aixs) # look up
    R = np.stack((x_aixs, y_axis, z_aixs))#, axis = 0) # 3 x 3
    transformed_vertices = vertices - eye # translation
    transformed_vertices = transformed_vertices.dot(R.T) # rotation
    return transformed_vertices

但是如果是旋转点, 假如旋转后点的坐标X’与旋转前X有如下关系:
$$R{X}^{\prime }=X$$
那么, 这个R矩阵则为:
$$R=[s,t]=\left[\begin{array}{cc}cos(\theta )& sin(\theta )\\ -sin(\theta )& cos(\theta )\end{array}\right]$$

台大机器人学之运动学-林沛群对旋转的介绍

旋转矩阵转为欧拉角时有两种方式，该视频将欧拉角分为Fixed Angels和Eular angels.

• Fixed angles（先做的旋转放后面, 参考外部坐标系）
  旋转时参考坐标系为一个固定坐标系($X_A,Y_A,Z_A$),

其中$R_B^A$代表从B到A的旋转，上图沿着X-Y-Z顺序做的旋转，所以旋转矩阵定义为：
$R_Z{R}_Y{R}_X$，先做的旋转放后面, 假如有点$P_a$, 那么可以通过公式$P_b=R_Z{R}_Y{R}_X{P}_a$将点p从a转到b坐标系。

• Eular Angles（先做的旋转放前面, 参考内部坐标系）
  Euler Angels指的是每次旋转参考的都是自身坐标系。这里以ZYX旋转顺序为例，可以看出$R_B^A$的构成是先做的旋转放前面。
  
  其实两种旋转方式调换顺序可以表示同一种旋转。
  
  

代码实现

可以使用scipy库中的Rotation 模块来做欧拉角到matrix的转换.
小写字母xyz代码参考坐标系为外部坐标系, 大写则为内部坐标系.

• 外部坐标系的转换测试

from scipy.spatial.transform import Rotation
import numpy as np
mat_x = Rotation.from_euler('x', 30, degrees = True).as_matrix()
mat_y = Rotation.from_euler('y', 40, degrees = True).as_matrix()
mat_z = Rotation.from_euler('z', 50, degrees = True).as_matrix()
my_rot_mat = mat_z @ mat_y @ mat_x
print(my_rot_mat)

mat_gt = Rotation.from_euler('xyz', [30, 40, 50], degrees = True).as_matrix()
print(mat_gt)

打印结果:

[[ 0.49240388 -0.45682599  0.74084306]
 [ 0.58682409  0.80287234  0.10504046]
 [-0.64278761  0.38302222  0.66341395]]
 
[[ 0.49240388 -0.45682599  0.74084306]
 [ 0.58682409  0.80287234  0.10504046]
 [-0.64278761  0.38302222  0.66341395]]

可以看出from_eular(‘xyz’)指的是先做x,后做y,最后z的变换, 对应矩阵上的操作就是mat_z @ mat_y @ mat_x

• 内部坐标系的转换测试

    mat_x = Rotation.from_euler('X', 30, degrees = True).as_matrix()
    mat_y = Rotation.from_euler('Y', 40, degrees = True).as_matrix()
    mat_z = Rotation.from_euler('Z', 50, degrees = True).as_matrix()
    my_rot_mat =  mat_x @ mat_y @ mat_z
    print(my_rot_mat)

    mat_gt = Rotation.from_euler('XYZ', [30, 40, 50], degrees = True).as_matrix()
    print(mat_gt)

打印:

[[ 0.49240388 -0.58682409  0.64278761]
 [ 0.8700019   0.31046846 -0.38302222]
 [ 0.02520139  0.74782807  0.66341395]]
 
[[ 0.49240388 -0.58682409  0.64278761]
 [ 0.8700019   0.31046846 -0.38302222]
 [ 0.02520139  0.74782807  0.66341395]]

也就印证了前面台大机器人学之运动学对而这转换的介绍.
总结下就是, 旋转参考坐标系为固定的外部坐标系时, 我们说的xyz旋转a,b,c度, 那么这个旋转矩阵就是: RzRyRz.如果参考坐标系为自身坐标系时, 这个旋转矩阵就是 RxRyRz.