GIOU翻译加自己的理解

Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression （2019 IEEE）

摘要

iou是目标检测基准中最常用的评估指标。然而，优化常用的回归边界盒参数的距离损失与最大化该度量值之间存在差距。度量的最优目标是度量本身。对于轴对称的二维边界盒，IoU可以直接作为一种回归损失。但是IoU有一个停滞期（plateau），使得在边界盒不重叠的情况下无法进行优化。在本文中，我们通过引入一个广义版本作为一个新的损失和一个新的度量来解决loU的弱点。通过将这种广义IoU (GIoU)作为一种损失纳入到最新的对象检测框架中，我们表明，在使用基于标准IoU和基于新的GIoU的流行对象检测基准(如PASCAL VOC和MS COCO)的性能度量时，它们的性能得到了一致的改善。

介绍

1、边界盒回归是许多2D/3D计算机视觉任务中最基本的组件之一。目标定位、多目标检测、目标跟踪和实例级分割等任务都依赖于准确的边界盒回归。利用深度神经网络提高应用程序性能的主要趋势是提出一种更好的体系结构骨干[15,13]或一种更好的策略来提取可靠的局部特征[6]。然而，一个被广泛忽视的改进机会是用基于交集对并(IoU)计算的度量损失来替代回归损失，如l1和l2-规范。
2、IoU，也被称为Jaccard指数，是比较两个任意形状之间相似度的最常用指标。IoU将被比较对象的形状属性(例如两个边框的宽度、高度和位置)编码到区域属性中，然后计算一个聚焦于它们的标准化度量区域(或卷)。这个性质使得IoU对所考虑问题的规模不变。由于这个吸引人的特性，用于评估分割[2,1,25,14]、目标检测[14,4]和跟踪[11,10]的所有性能度量都依赖于这个度量。
3、然而，可以看出，将二维/三维中两个边框参数表示中定义的ln -范数等常用损失最小化与提高其IoU值之间并没有很强的相关性。例如，考虑图1 (a)中简单的2D场景，其中预测的边界盒(黑色矩形)和ground truth盒(绿色矩形)用它们的左上角和右下角表示，即(x1, y1, x2,y2)。为了简单起见，我们假设两个盒子的一个角之间的距离(例如l2-norm)是固定的。因此，任何第二个角位于以绿色矩形(以灰色虚线圆表示)第二个角为圆心的圆上的预测边界盒与圆真盒的l2-范数距离将完全相同;然而，它们的IoU值可能有显著差异(图1 (a))。同样的论证可以推广到任何其他的表述和损失，例如图1 (b)。这是直观的，一个好的局部最优为这些类型的目标可能不一定是局部最优loU。此外，与IoU相比，基于上述参数表示定义的ln-norm目标对问题的规模不是不变的。不是随着问题的规模而不变的。为了达到这一目的，由于透视等原因，几对具有相同重叠级别但不同尺度的边界盒会产生不同的客观值。此外，一些表示可能会因为用于表示的不同类型的参数之间缺乏正则化而受到影响。例如，在中心和大小表示中，(cc, yc)定义在位置空间上，(w, h)属于大小空间。复杂性随着更多参数的加入而增加。旋转，或者增加更多维度的问题。为了缓解前面提到的一些问题，最新的对象检测器引入了锚盒[22]的概念，作为假设的良好初始猜测。他们还定义了一个非线性表示[19,5]，以天真地补偿规模的变化。即使使用这些手工更改，在优化回归损失和IoU值之间仍然存在差距。

4、在本文中,我们探索的计算两个轴对齐矩形之间的iou,或两轴对齐北纬,一个简单的解析解,与流行的信念,iou在这种情况下可以反向传播[24],即可以直接使用它作为优化的目标函数。因此，在二维目标检测任务中，最好使用iou作为目标函数。在优化度量本身和替代损失函数之间进行选择，最优选择是度量本身。然而，iou作为衡量标准和损失都有一个重要的意义主要问题:如果两个物体不重叠，IoU值将为零，并不能反映两个形状之间的距离。在不重叠对象的情况下，如果将IoU作为损失，其梯度将为零，无法进行优化。
5、在本文中，我们将通过将借据的概念扩展到不重叠的情况来解决借据的这个弱点。我们确保该泛化(a)遵循与IoU相同的定义，即将比较对象的形状属性编码到区域属性中;(b)保持IoU的尺度不变性，©保证在对象重叠的情况下，IoU与IoU具有很强的相关性。我们引入了IoU的广义版本，称为GIoU，作为比较任意两种形状的新度量。我们还提供了计算两个轴向矩形之间的GIoU的解析解，允许它在这种情况下用作损失。将GIoU损失纳入到最新的对象检测算法中，我们通过使用基于IoU的标准[4,14]和新的基于GIoU的标准，不断提高它们在流行的对象检测基准(如PASCAL VOC[4]和MS COCO[14])上的性能。性能的措施。
6、总结了本文的主要贡献:
我们引入了GIOU，作为比较任意两种形状的新度量。
我们提供了一个用GIoU作为两个轴对齐矩形之间的损失的解析解n- orthotopes
我们将GIoU损失纳入最流行的对象检测算法，如Faster R-CNN, Mask R-CNN和YOLO v3。并在标准目标检测基准上展示了它们的性能改进。

相关工作

1、目标检测精度度量:
IoU是在目标检测中实际使用的评估度量。它用于确定一组预测中的真阳性和假阳性。**当使用loU作为评价指标时，必须选择一个精度阈值。**例如，在PASCAL VOC挑战[4]中，广泛报道的检测精度测量，**即平均平均精度(mAP)，**是基于固定的IoU阈值计算的，即0.5。然而，任意选择IoU阈值并不能充分反映不同方法的定位性能。任何高于阈值的定位精度都被同等对待。为了使这个性能测量对IoU阈值的选择不那么敏感，MS COCO基准挑战[14]平均地图跨越多个IoU阈值。
2、边界盒表示与损失:
在二维目标检测中，学习边界盒参数是至关重要的。文献中提出了各种边界盒表示和损失。Redmon等人在YOLO v1[19]中提出了对边界盒参数的直接回归，并对边界盒大小进行了小调整，以预测边界盒大小的平方根，以弥补比例灵敏度。在RCNN中，Girshick等人[5]通过预测使用选择性搜索算法[23]计算的先验边界框的位置和大小偏移量来参数化边界框表示。为降低表示的尺度敏感性，在对数空间中定义边界盒大小偏移量。然后，使用l2-norm目标，也称为MSE损失，作为优化的目标。随后，在Fast R-CNN[7]中，Girshick提出了1-smooth loss来提高学习对异常值的鲁棒性。Ren等人[22]提出使用一组密集的先验边界盒，即锚盒，然后回归到边界盒位置和大小的小变化。但是，由于正样本和负样本之间存在显著的类不平衡，使得训练边界框得分更加困难。为了减轻这个问题，作者后来引入了焦点损失[131，这是正交于我们的论文的主要焦点。
3、大多数流行的物体探测器[20,21,3,12,13,16]利用了上面提到的包围盒表示和损耗的某种组合。这些相当大的努力已经在目标检测方面取得了显著的改进。我们认为，使用GIoU可能有进一步改进定位的机会，因为它们的边界框回归损失不能直接代表核心评估指标，即IoU。
4、使用近似函数或代理函数优化IoU:在语义分割任务中，使用近似函数[18]或代理函数[17]优化IoU。同样，对于目标检测任务，最近的研究[8,24]也试图直接或间接地纳入IoU，以更好地执行边界盒回归。但是，在非重叠情况下，在优化IoU时，它们会遇到近似或停滞期问题。在本文中，我们通过引入一个广义的iou来解决iou的缺点，并直接将其作为对象检测问题的损失。

优化iou

比较两个任意形状(体积)A, B ⊆ S ∈ Rn的LoU由:
以下两个吸引人的特征使得这种相似性度量在评价许多2D/3D计算机视觉任务时很受欢迎:
1、IoU作为距离，例如Iou损失 = 1-IoU，是一个度量(通过数学定义)[9]。这意味着lou损失满足了metric的非负性、不可分辨恒等式、对称性和三角形不等式等所有性质。
2、IoU不随问题的规模而变化。这意味着两个任意形状A和B之间的相似性独立于它们的空间S的尺度(证据在材料中提供)。
然而：
如果|AnBI=0, IoU(A, B) =0。在这种情况下，IoU“不反映两个形状是在彼此附近还是离得很远”。
为了解决这个问题，我们提出了Giou，
对于两个任意凸形状(体积)A, B ⊆ S ∈ Rn，我们首先找到包含A和B2的最小凸形状C ⊆ S ∈ Rn 。为了比较两种特定类型的几何形状，C可以是同一类型的。例如，两个任意的椭球，C可以是包围它们的最小的椭球。然后我们计算体积(地区)之间的比例被C排除a和B的和除以总量(地区)被C。这代表了一个规范化的措施,着重于空体积(地区)a和B之间最后GIoU达到减这个比例借据的价值。GIoU的计算总结在算法1中。
说白了：GIOU就等于iou减去包围A，B的C除去A和B剩下的部分在C中的占比


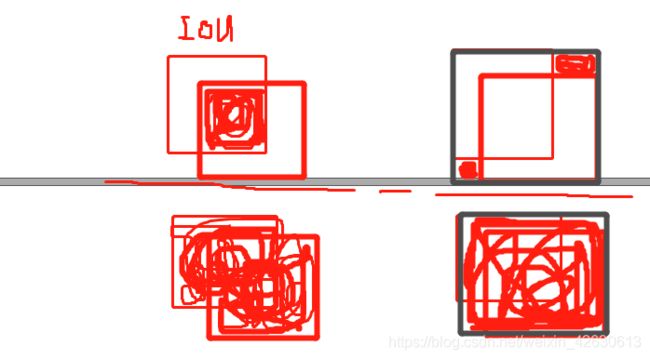
GIOU的特性：
1、与IoU相似，GIoU作为距离，如Glou损失 = 1-GIoU，具有度规的所有性质，如非负性、不可分辨的同一性、对称性和三角形不等式。
2、Giou不随问题的规模而变化
3、GIOU总是低于IOU的边界，i.e. ∀A, B ⊆S GIoU(A, B) ≤ IoU(A, B) ，当A和B的形状和距离相似性更强时，这个较低的边界变得更紧
i.e. limA→B GIoU(A, B) =IoU(A, B).
4、∀A, B ⊆ S, 0 ≤ IoU(A, B) ≤ 1 但是GIOU有一个对称的范围，i.e. ∀A, B ⊆ S, -1 ≤GIoU(A, B) ≤ 1
与IoU类似，1只在2物体出现完美地叠加，即如果|A∪B| = |A∩B|，那么GIoU = IoU = 1
当两种形状的占据区域|A∪B|与包围形状|C|的体积(面积)之比趋于零时，GIoU值渐近收敛于-1

综上所述，这一推广保留了IolU的主要性质，同时修正了它的弱点。因此，在2D/3D计算机视觉任务中使用的所有性能指标中，GIoU可以作为loU的适当替代品。在本文中，我们只关注二维目标检测，我们可以很容易地推导出GIoU的解析解，以应用它作为度量和损失。扩展到非轴向对齐的三维情况是留给未来的工作。
GIoU作为边界盒回归的损失
到目前为止，我们介绍了GIoU作为任意两个任意形状的度量。然而，就像loU的情况一样，没有解析解来计算两个任意形状之间的交集和/或为它们找到最小的封闭凸对象。
幸运的是，对于2D目标检测任务，其中的任务是比较两个轴对齐的边界盒，我们证明GIoU有一个直接的解决方案。在这个例子中，交集和最小的封闭对象都是矩形。结果表明，它们的顶点坐标只是比较两个边界盒中的一个的坐标，可以通过使用最小和最大函数比较每个顶点的坐标来获得。若要检查两个边框是否重叠，还必须检查一个条件。因此，我们有一个精确的计算IoU和GIol的方法。
由于反向传播最小、最大和分段线性函数(如Relu)是可行的，可以证明算法2中的每个分量都有一个表现良好的导数。因此，IoU或GIoU可以直接作为一种损失，即CIoU或LGIoU，用于基于深度神经网络的目标检测器的优化。在这种情况下，我们直接优化一个度量作为损失，这是一个最优选择的度量。但是，在所有不重叠的情况下，IoU的梯度都为零，这影响了训练质量和收敛速度。相比之下，GIoU在所有可能的情况下都有梯度，包括不重叠的情况。另外，利用性质3，

归纳一下
输入是预测框和真实框坐标
输出是IOU损失和GIOU损失

计算过程
先决条件
1、计算真实框面积，
2、计算预测框面积
3、计算真实框和预测框相交的面积
4、找预测框和真实框的最小的包围框
5、计算包围框的面积
IOU=交的面积/并的面积，并的面积=两个框面积之和减去交的面积
GIOU=IOU-（最小包围框面积-交的面积）/最小包围框面积
IOU损失=1-IOU
GIOU损失=1-GIOU

我们发现GIoU与IoU有很强的相关性。特别是在高Iol值。我们也在图2中定性地展示了这种相关性，通过从两个2D矩形的坐标中抽取超过10K的随机样本。在图2中，我们还观察到，在低重叠的情况下，例如。IoU <0.2和GIoU <0.2, GIoU有机会。与借据相比变化更大。为此。与人工晶体相比，在这些情况下，GIoU在任何可能的状态下都可能有一个更陡的梯度。因此，无论最终采用哪种基于iou的绩效指标，Ccolr都是优化GIoU的较好选择。我们的实验结果证实了这一说法。
损失稳定性:我们还研究了是否存在其他特殊情况，对于给定任何值的预测输出，使损失不稳定/不确定。

∀ 为任意
考虑到ground truth边界框 ，Bg（真实框）是一个面积（area）大于0的矩形框，即Ag（真实框面积）＞0，
算法2（1）和在算法2（4）中各自的条件确保预测区域Ap（真实框面积）和交I是非负的，即Ap ≥ 0 and I ≥ 0 ∀Bp ∈ R4 。
因此对于任意Bp（预测框） = (xp 1, y1p, xp 2, y2p) ∈ R4 的预测值，并U＞0，这确保了IoU中的分母对于输出的任何预测值都不能为零。
对Bp（预测框） = (xp 1, y1p, xp 2, y2p) ∈ R4来说，并U总是比交I大，即U≥I，
因此，IOU损失总是有边界的，即0≤IOU损≤1∀Bp ∈ R4

为了核实GOIU损失的稳定性，额外的测试，即Ac-U/Ac， 应该总是一个确定的、有边界的值。
对于所有的预测值，最小的封闭盒子Bc不能比Bg更小，因此Ac总是一个正非零数，因为Ac≥Ag∀Bp ∈ R4 and Ag ≥ 0 。
对于任何预测值，最小封闭盒的面积都不能小于并集，即Ac ≥ U∀Bp ∈ R4 ，
因此，在GIOU中额外的测试是正的有边界的，因此GIOU损失是有边界的，即0 ≤ GIoU损失 ≤ 2 ∀Bp ∈ R4

IOU为0时GIOU损失：对于GIOU损失，GIOU损失=1-GIOU=1+（Ac-U） /Ac- IoU ,在Bg和Bp不重叠的情况下，即I=0且IOU=0，
GIOU损失可以简化为GIOU损失=1+（Ac-U） /Ac=2-U/Ac，
通过最小化GIOU损失，可以最大化U/Ac，这是一个归一化到0-1之间的操作，即0≤U/Ac≤1，最大的时候，最小的封闭盒Ac的面积是最小的，而union U = Ag +Ap，更准确地说是预测的边界盒Ap的面积最大。
为了实现这一点，预测的边界盒Bp的顶点应该朝着鼓励Bg和Bp重叠的方向移动，令iou = 0。

结论

在本文中，我们将广义的IoU为一个新的度量，即GIoU，用于比较任意两个形状。我们证明了这个新的度量具有IoU所具有的所有吸引人的特性，同时也解决了它的弱点。因此，它可以是一个很好的替代方案，在所有性能测量在2D/3D视觉任务依赖IoU 指标中。并给出了计算两个轴对齐矩形间GIoU的解析解。我们证明了可以计算GIoU作为距离的导数，并将其作为边界盒回归损失。通过将其融入到最先进的对象检测算法中，我们在流行的对象检测基准(如PASCAL VOO和MS COCO)上不断提高了它们的性能，使用了常用的性能度量和我们新的精度度量，即基于平均精度的GIoU。由于度量的最优损失是度量本身，因此我们的GIoU损失可以在所有需要2D边界盒回归的应用中用作最优边界盒回归损失。

注：一句一句翻译完，看比自己看网上别人的翻译收获更多