读书笔记-白话机器学习的数学

回归

线性回归

步骤

1. 训练数据，画图
2. 预测函数和目标函数
   • 初始值是随机的
   • 最小二乘法
   • $\frac{1}{2}$ 是方便计算加的
3. 梯度下降法
   • 学习率 $\eta$
4. 复合函数微分的链式法则
5. 参数更新表达式
6. 演示程序
7. 标准化
   • 差值阈值，跳出训练

公式

预测函数:
$$f_{\theta }(x)={\theta }_0+{\theta }_{1}x$$
目标函数（误差函数）：
$$E(\theta )=\frac{1}{2}\sum _{i=1}^n(y^{(i)}-f_{\theta }(x^{(i)}){)}^2$$
梯度下降法表达式：
$${\theta }_0:={\theta }_0-\eta \frac{\partial E}{\partial {\theta }_0}$$
链式法则：
$$\begin{gathered} u=E(\theta ) \\ v=f_{\theta }(x) \\ \frac{\partial u}{\partial {\theta }_0}=\frac{\partial u}{\partial v}\cdot \frac{\partial v}{\partial {\theta }_0} \end{gathered}$$

参数更新表达式：

$u$ 对 $v$ 的微分

$$\begin{gathered} \frac{\partial u}{\partial v}=\frac{\partial }{\partial v}(\frac{1}{2}\sum _{i=1}^n(y^{(i)}-v{)}^2) \\ =\frac{1}{2}\sum _{i=1}^n(\frac{\partial }{\partial v}(y^{(i)}-v{)}^2) \\ =\frac{1}{2}\sum _{i=1}^n(\frac{\partial }{\partial v}(y^{(i{)}^2}+v^2-2y^{(i)}v)) \\ =\frac{1}{2}\sum _{i=1}^n(2v-2y^{(i)}) \\ =\sum _{i=1}^n(v-y^{(i)}) \end{gathered}$$

$v$ 对${\theta }_0$ 的微分

$$\begin{gathered} \frac{\partial v}{\partial {\theta }_0}=\frac{\partial }{\partial {\theta }_0}({\theta }_0+{\theta }_{1}x) \\ =1 \end{gathered}$$
$u$ 对 ${\theta }_0$ 的微分

$$\begin{gathered} \frac{\partial u}{\partial {\theta }_0}=\frac{\partial u}{\partial v}\cdot \frac{\partial v}{\partial {\theta }_0} \\ =\sum _{i=1}^n(v-y^{(i)})\cdot 1 \\ =\sum _{i=1}^n(f_{\theta }(x^{(i)})-y^{(i)}) \end{gathered}$$
${\theta }_0$ 的参数更新表达式：
$${\theta }_0:={\theta }_0-\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})-y^{(i)})$$
同理，${\theta }_1$ 的参数更新表达式：
$${\theta }_1:={\theta }_1-\eta \sum _{i=1}^n(f_{\theta }(x^{(i)})-y^{(i)})x^{(i)}$$

使用矩阵表示

预测函数:
$$f_{\theta }(x)={\theta }_0+{\theta }_{1}x$$
使用向量表示：
$$\theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\end{array}\right]x^{(i)}=\left[\begin{array}{c}1\\ x^{(i)}\end{array}\right]$$

优化算法

• 最速梯度下降法的缺点
  • 计算量大
  • 容易陷入局部最优解
• 随机梯度下降
  • 随机选择一个训练数据来更新参数
  • 最速下降法更新一次，随机梯度下降法可以更新 n 次
• 小批量梯度下降法
  • 随机选择 m 个训练数据来更新参数

问题

为什么要使用梯度下降法，直接求导不行吗？

1. 确定不了导数为 0 的时候，是最大值还是最小值
2. 计算机更擅长循环迭代的方式求解
3. 多元表达式无法直接求解

为什么使用标准化？

• 提升模型精度
• 提升收敛速度
• 不改变原始数据的分布

为什么是用 python 作为 AI 的主流语言？

• 广泛的库和框架选择
• 平台独立性

学习率如何决定？

目前只能通过反复尝试来找到合适的值

扩展

• 多重回归
  • 对参数进行标准化，校验时需要使用相同的平均数和标准差
• 多项式回归

分类

感知机

• 只能处理线性可分的情况
• 可以处理三维以上的数据

步骤

1. 训练数据，画图
   • 矩形为横向还是纵向
2. 预测函数和目标函数
   • $x$ 和 $w$为向量
   • 内积正负说明相似程度
   • 无目标函数
3. 参数更新表达式
   • 寻找使权重向量成为法线向量的直线
   • 通过向量的相加实现权重的更新
4. 演示程序
   • 指定训练次数

公式

预测函数（判别函数）：
$$f_{\mathbf{w}}(\mathbf{x})=\{\begin{array}{ll}1& (\mathbf{w}\cdot \mathbf{x}\ge 0)\\ -1& (\mathbf{w}\cdot \mathbf{x}<0)\end{array}$$
参数更新表达式：
$$\mathbf{w}:=\{\begin{array}{ll}\mathbf{w}+y^{(i)}\mathbf{x}& (f_{\mathbf{w}}({\mathbf{x}}^{(i)})\ne y^{(i)})\\ \mathbf{w}& \end{array}$$

逻辑回归

• y 值使用 0 和 1 处理更加方便
• 训练数据
  • 线性可分
  • 同感知机
• 预测函数
  • ${\theta }^T\mathbf{x}=0$ 时，值为 0.5
  • 函数值在（0，1）范围内
  • ${\theta }^T\mathbf{x}=0$ 时的直线称为决策边界
• 目标函数
  • 似然函数，Likelihood
  • 派
  • 求使目标函数最大化的参数$\theta$
• 参数更新表达式
  • $log(1-v)$ 同样使用复合函数求导公式进行微分
  • 指定训练次数

公式

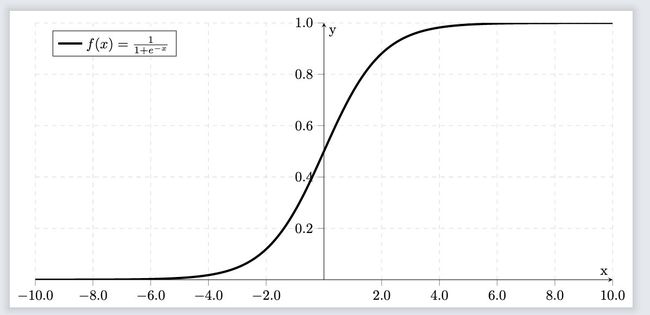
sigmoid函数:
$$\sigma (x)=\frac{1}{1+e^{-x}}$$

常用导数：
$$\begin{gathered} (e^x{)}^{\prime }=e^x \\ (e^{-x}{)}^{\prime }=-e^{-x} \end{gathered}$$
sigmoid函数微分:

$$\begin{gathered} {\sigma }^{\prime }(x)=-\frac{(1+e^{-x}{)}^{\prime }}{(1+e^{-x}{)}^2} \\ =\frac{e^{-x}}{(1+e^{-x}{)}^2} \\ =\frac{1}{1+e^{-x}}-\frac{1}{(1+e^{-x}{)}^2} \\ =\sigma (x)(1-\sigma (x)) \end{gathered}$$
预测函数：
$$\begin{gathered} f_{\theta }(\mathbf{x})=\frac{1}{1+\exp (-{\theta }^T\mathbf{x})} \\ {\theta }^T\mathbf{x}=({\theta }_0{x}_0+{\theta }_1{x}_1+\dots +{\theta }_n{x}_n) \end{gathered}$$
阈值函数：
$$y=\{\begin{array}{ll}1& ({\theta }^T\mathbf{x}\ge 0)\\ 0& ({\theta }^T\mathbf{x}<0)\end{array}$$
未知数据 $\mathbf{x}$是横向图像的概率：
$$P(y=1|\mathbf{x})=f_{\theta }(\mathbf{x})$$
目标函数：
$$L(\theta )=\prod _{i=1}^{n}P(y^{(i)}=1|{\mathbf{x}}^{(i)}{)}^{y^{(i)}}P(y^{(i)}=0|{\mathbf{x}}^{(i)}{)}^{1-y^{(i)}}$$
对数似然函数：
$$\begin{gathered} \log L(\theta )=\log \prod _{i=1}^{n}P(y^{(i)}=1|{\mathbf{x}}^{(i)}{)}^{y^{(i)}}P(y^{(i)}=0|{\mathbf{x}}^{(i)}{)}^{1-y^{(i)}} \\ =\sum _{i=1}^n(\log P(y^{(i)}=1|{\mathbf{x}}^{(i)}{)}^{y^{(i)}}+\log P(y^{(i)}=0|{\mathbf{x}}^{(i)}{)}^{1-y^{(i)}}) \\ =\sum _{i=1}^n(y^{(i)}\log P(y^{(i)}=1|{\mathbf{x}}^{(i)})+(1-y^{(i)})\log P(y^{(i)}=0|{\mathbf{x}}^{(i)})) \\ =\sum _{i=1}^n(y^{(i)}\log P(y^{(i)}=1|{\mathbf{x}}^{(i)})+(1-y^{(i)})\log (1-P(y^{(i)}=1|{\mathbf{x}}^{(i)}))) \\ =\sum _{i=1}^n(y^{(i)}\log f_{\theta }({\mathbf{x}}^{(i)})+(1-y^{(i)})\log (1-f_{\theta }({\mathbf{x}}^{(i)}))) \end{gathered}$$
复合函数：
$$\begin{gathered} u=\log L(\theta ) \\ v=f_{\theta }(\mathbf{x}) \end{gathered}$$
参数更新表达式：

$u$ 对$v$的微分
$$\begin{gathered} \frac{\partial u}{\partial v}=\frac{\partial }{\partial v}\sum _{i=1}^n(y^{(i)}\log (v))+(1-y^{(i)})\log (1-v)) \\ =\sum _{i=1}^n(\frac{y^{(i)}}{v}-\frac{1-y^{(i)}}{1-v}) \end{gathered}$$
$v$ 对 ${\theta }_j$ 微分
$$\begin{gathered} \frac{\partial v}{\partial {\theta }_j}=\frac{\partial }{\partial {\theta }_j}\frac{1}{1+\exp (-{\theta }^T\mathbf{x})} \\ =v(1-v)\cdot x_j \end{gathered}$$
$u$ 对 ${\theta }_j$ 微分
$$\begin{gathered} \frac{\partial u}{\partial {\theta }_j}=\frac{\partial u}{\partial v}\cdot \frac{\partial v}{\partial {\theta }_j} \\ =\sum _{i=1}^n(\frac{y^{(i)}}{v}-\frac{1-y^{(i)}}{1-v})\cdot v(1-v)\cdot x_j^{(i)} \\ =\sum _{i=1}^n(y^{(i)}(1-v)-(1-y^{(i)})v)x_j^{(i)} \\ =\sum _{i=1}^n(y^{(i)}-y^{(i)}v-v+y^{(i)}v)x_j^{(i)} \\ =\sum _{i=1}^n(y^{(i)}-v)x_j^{(i)} \\ =\sum _{i=1}^n(y^{(i)}-f_{\theta }(\mathbf{x}))x_j^{(i)} \end{gathered}$$
${\theta }_j$ 的参数更新表达式：
$${\theta }_j={\theta }_j+\eta \sum _{i=1}^n(y^{(i)}-f_{\theta }(\mathbf{x}))x_j^{(i)}$$
${\theta }_j$ 的参数更新表达式（和回归时保持一致）：
$${\theta }_j={\theta }_j-\eta \sum _{i=1}^n(f_{\theta }(\mathbf{x})-y^{(i)})x_j^{(i)}$$
决策边界：
$$\begin{gathered} {\theta }^T\mathbf{x}={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2 \\ {x}_2=-\frac{{\theta }_0+{\theta }_1{x}_1}{{\theta }_2} \end{gathered}$$

线性不可分

• 多项式函数
• 决策边界为曲线

决策边界：
$$\begin{gathered} {\theta }^T\mathbf{x}={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2 \\ {x}_2=-\frac{{\theta }_0+{\theta }_1{x}_1+{\theta }_3{x}_1^2}{{\theta }_2} \end{gathered}$$

扩展

• SVM 分类算法
• 其他分类算法

正则化

1. 确定正则化项
   • $\lambda$ 表示正则化项影响程度
2. 重定义目标函数
3. 重定义参数更新表达式

公式

L2正则化项：
$$R(\theta )=\frac{\lambda }{2}\sum _{j=1}^m{\theta }_j^2$$
目标函数：
$$E(\theta )=\frac{1}{2}\sum _{i=1}^n(y^{(i)}-f_{\theta }({\mathbf{x}}^{(i)}){)}^2+\frac{\lambda }{2}\sum _{j=1}^m{\theta }_j^2$$

参数更新表达式：
$$\begin{gathered} {\theta }_0:={\theta }_0-\eta (\sum _{i=1}^n(f_{\theta }({\mathbf{x}}^{(i)})-y^{(i)})x_j^{(i)}) \\ {\theta }_j:={\theta }_j-\eta (\sum _{i=1}^n(f_{\theta }({\mathbf{x}}^{(i)})-y^{(i)})x_j^{(i)}+\lambda {\theta }_j))(j>0) \end{gathered}$$

基础

• 误差函数

  • MSE(Mean Square Error, 均方误差)，$\frac{1}{n}{\sum }_{i=1}^n(y^{(i)}-f_{\theta }({\mathbf{x}}^{(i)}){)}^2$
  • SSE(The Sum Of Squares Due To Error, 和方差)
  • RMSE(Root Mean Squared Error, 均方根误差)

• 容量

  • batchsize：批大小
  • iteration：1 个iteration 等于使用 batchsize 个样本训练一次
  • epoch：1个epoch等于使用训练集中的全部样本训练一次

• 随机梯度下降法（Stochastic Gradient Descent，SGD)

模型评估

• 交叉验证：将数据按一定比例分为测试数据和训练数据，一般为 3:7 或者 2:8
• 数据的分配方法不能太极端
• 回归问题：均方误差
• 计算精确率和召回率时使用数据少的类别
• K 折交叉验证：需要确定一个合适的 K 值
• 学习曲线：通过学习曲线判断模型是过拟合还是欠拟合
  • 高偏差(欠拟合)：随着数据数量的增加，使用训练数据时的精度不断下降，使用测试数据时的精度不断上升
  • 高方差(过拟合)：随着数据数量的增加，使用训练数据时的精度缓慢，使用测试数据时的精度不断上升，但是达不到训练数据精度

分类问题

• 精度

$$Accuracy=\frac{TP+TN}{TP+FP+FN+TN}$$

• 精确率：当训练数据极不平衡时，在分类为 Positive 的数据中，分类正确的比例

$$Precision=\frac{TP}{TP+FP}$$

• 召回率：在 Positive 数据中，分类正确的比例
  $$Recall=\frac{TP}{TP+FN}$$

• 一般来说，精确率和召回率会一个高一个低，不能取平均值

• 调和平均值F1值：
  $$\begin{gathered} Fmeasure=\frac{2}{\frac{1}{Precision}+\frac{1}{Recall}} \\ Fmeasure=\frac{2\cdot Precision\cdot Recall}{Precision+Recall} \end{gathered}$$

• 权重调和平均值F值：
  $$Fmeasure=\frac{(1+{\beta }^2)\cdot Precision\cdot Recall}{{\beta }^2\cdot Precision+Recall}$$

正则化

过拟合

• 过拟合：只能拟合训练数据
• 避免过拟合
  • 增加全部训练数据的数量（重要）
  • 使用简单的模型，例：将预测函数从曲线变成直线
  • 正则化
• 欠拟合：一般模型过于简单

正则化

• 防止参数变得过大，减少参数的影响，对参数进行惩罚
• 不对偏置项进行正则化
• $\lambda$ 为正则化项影响程度
• 线性回归的正则化
  $$\begin{gathered} E(\theta )=\frac{1}{2}\sum _{i=1}^n(y^{(i)}-f_{\theta }(x^{(i)}){)}^2 \\ R(\theta )=\frac{\lambda }{2}\sum _{j=1}^m{\theta }_j^2 \end{gathered}$$
• 分类函数的正则化，改变目标函数的符号将最大化问题转换为最小化问题
  $$\log L(\theta )=-\sum _{i=1}^n(y^{(i)}\log f_{\theta }({\mathbf{x}}^{(i)})+(1-y^{(i)})\log (1-f_{\theta }({\mathbf{x}}^{(i)})))+\frac{\lambda }{2}\sum _{j=1}^m{\theta }_j^2$$
• L1 正则化：被判定为不需要的参数为变为 0
  $$R(\theta )=\lambda \sum _{j=1}^m|{\theta }_j|$$
• L2 正则化：抑制参数
  $$R(\theta )=\frac{\lambda }{2}\sum _{j=1}^m{\theta }_j^2$$

参考

• 数据集 Iris

待学习

• numpy
• Matplotlib Pyplot