LPA算法原理
LPA算法学习记录
- 算法原理
-
- 构建完全图(W矩阵)
- 概率传播矩阵(P矩阵)
- 标签矩阵(F矩阵)
- 迭代过程
- python代码实现:
算法原理
标签传播算法作为一种直推式学习方法,其被应用到了小样本学习中,以试图解决数据量过少的问题。本文主要阐述最简单的LPA原理
构建完全图(W矩阵)
W矩阵是一个N * N的矩阵,由它代表完全图,很明显,这是一个对称的方阵,N表示结点数量。 w i j w_{ij} wij表示结点 N j N_j Nj与 N i N_i Ni之间的相似度。相似度计算公式为:
w i j = exp ( − d i j σ 2 ) = exp ( − ∑ d = 1 D ( x i d − x j d ) σ 2 ) w_{\mathrm{ij}}=\exp \left(-\frac{\mathrm{d}_{\mathrm{ij}}}{\sigma^2}\right)=\exp \left(-\frac{\sum_{\mathrm{d}=1}^{\mathrm{D}}\left(\mathrm{x}_{\mathrm{i}}^{\mathrm{d}}-\mathrm{x}_{\mathrm{j}}^{\mathrm{d}}\right)}{\sigma^2}\right) wij=exp(−σ2dij)=exp(−σ2∑d=1D(xid−xjd))
在代码实现过程中, d i j d_{ij} dij采用的是欧式距离, σ \sigma σ是一个超参数。
概率传播矩阵(P矩阵)
标签传播,重点在于传播,一个结点与其余结点都有连接,都会被其他的结点所影响,但是根据 w i j w_{ij} wij的不同,其影响程度也不同,因此P矩阵实际上是W矩阵按行归一化的结果。即相似度越高,影响权重越大。这里给到一个从W转为P的示例:

当数据确定后,结点之间的相似度也就确定了,因此P矩阵在整个计算过程中都不会发生改变。
标签矩阵(F矩阵)
在我看来,这实际上就是一个概率矩阵,行代表样本,列代表类别, F i j F{ij} Fij代表样本 i i i属于类 j j j的概率。在经过不断迭代使其收敛后,根据概率大小判断样本类别,示例如下图:

图中N1,N2代表标记数据,N3,N4代表未标记数据。由于标记数据的标签是确定的,所以其概率设为1,其他类别概率为0。比如图中N1属于C3类,则其值为1,其余为0,N2同理。未标记数据的概率则无所谓了,反正都要迭代生成,不影响结果。
迭代过程
迭代过程就是所谓的”传播过程“,其旨在不断更新F矩阵,使其收敛。因此计算公式很简单:F = P * F。 但是在每次迭代后,要将标记数据的标签重置回来,因为他们的标签是确定的。
python代码实现:
import numpy as np
import math
import matplotlib.pyplot as plt
def buildGraph(MatX, rbf_sigma=None):
"""
构建完全图,方阵,行列大小均为结点数量
每个元素按照定义初始化
:param MatX: 全体数据矩阵
:param rbf_sigma: 计算公式里的参数
:return: 返回矩阵P
"""
num_samples = MatX.shape[0]
affinity_matrix = np.zeros((num_samples, num_samples), np.float32)
if rbf_sigma == None:
raise ValueError("rbf_sigma can't be None!")
for i in range(num_samples):
row_sum = 0.0
for j in range(num_samples):
diff = MatX[i, :] - MatX[j, :]
affinity_matrix[i][j] = np.exp(sum(diff ** 2) / (-2.0 * rbf_sigma ** 2))
row_sum += affinity_matrix[i][j]
affinity_matrix[i][:] /= row_sum
return affinity_matrix
def native_knn(dataset, query, k):
num_samples = dataset.shape[0]
diff = np.tile(query, (num_samples, 1)) - dataset
square_diff = diff ** 2
square_distance = np.sum(square_diff, axis=1)
sorted_indexs = np.argsort(square_distance)
if k > num_samples:
k = num_samples
return sorted_indexs[0:k]
def build_graph_knn(mat_x, k=None):
if k is None:
raise ValueError("k is NULL!")
num_samples = mat_x.shape[0]
affinity_matrix = np.zeros((num_samples, num_samples), np.float32)
for i in range(num_samples):
k_neighbors = native_knn(mat_x, mat_x[i,:], k)
affinity_matrix[i][k_neighbors] = 1.0 / k
return affinity_matrix
def labelPropagation(Mat_Label, Mat_Unlabel, labels, rbf_sigma=1.5, max_iter=500, tol=1e-3):
"""
:param Mat_Label: 标记的数据
:param Mat_Unlabel: 没有标记的数据
:param labels: 所有数据的标签,长度为结点数量
:param rbf_sigma: 计算公式里的参数
:param max_iter: 最大迭代次数
:param tol: 最小误差
:return: 直接返回未标记数据的标签
"""
num_label_samples = Mat_Label.shape[0]
num_unlabel_samples = Mat_Unlabel.shape[0]
num_samples = num_label_samples + num_unlabel_samples
labels_list = np.unique(labels)
num_classes = len(labels_list) # 得到F矩阵的列数,就是种类的个数
Mat_X = np.vstack((Mat_Label, Mat_Unlabel)) # 将两个数据矩阵按行堆叠,得到所有的数据
clamp_data_label = np.zeros((num_label_samples, num_classes), np.float32) # 对于已标记数据的标签矩阵的初始化
for i in range(num_label_samples):
clamp_data_label[i][labels[i]] = 1.0 # 属于哪个类,则哪个类对应的列的位置置为1
label_function = np.zeros((num_samples, num_classes), np.float32) # 初始化总体的F矩阵
label_function[0: num_label_samples][:] = clamp_data_label # 将已标记数据初始化
label_function[num_label_samples:num_samples] = -1 # 将未标记数据的标签随便初始化
affinity_matrix = buildGraph(Mat_X, rbf_sigma) # 首先得到P矩阵
iter = 0
pre_label_function = np.zeros((num_samples, num_classes), np.float32) # 每次迭代都会产生预测结果,这个用于记录上一次的label_function
changed = np.abs(pre_label_function - label_function).sum()
while iter < max_iter and changed > tol:
print("---> Iteration %d/%d, changed:%f" % (iter, max_iter, changed))
pre_label_function = label_function
iter += 1
label_function = np.dot(affinity_matrix, label_function) # 按照公式计算
# label_function = np.vstack((clamp_data_label,label_function[num_label_samples]))
label_function[:num_label_samples] = clamp_data_label # 每次都需要将标签数据从新赋为初始的标签,这个是不可以变的
changed = np.abs(pre_label_function - label_function).sum() # 计算迭代前后的一个损失
unlabel_data_labels = np.zeros(num_unlabel_samples) # 初始化未标记数据的预测标签
for i in range(num_unlabel_samples):
unlabel_data_labels[i] = np.argmax(label_function[i + num_label_samples]) # 最终得到的标记矩阵,每一行是该数据属于哪个类的概率分布,取最大的为预测值
return unlabel_data_labels
def labelPropagation_knn(Mat_Label, Mat_Unlabel, labels, k=10, max_iter=500, tol=1e-3):
"""
:param Mat_Label: 标记的数据
:param Mat_Unlabel: 没有标记的数据
:param labels: 所有数据的标签,长度为结点数量
:param rbf_sigma: 计算公式里的参数
:param max_iter: 最大迭代次数
:param tol: 最小误差
:return: 直接返回未标记数据的标签
"""
num_label_samples = Mat_Label.shape[0]
num_unlabel_samples = Mat_Unlabel.shape[0]
num_samples = num_label_samples + num_unlabel_samples
labels_list = np.unique(labels)
num_classes = len(labels_list) # 得到F矩阵的列数,就是种类的个数
Mat_X = np.vstack((Mat_Label, Mat_Unlabel)) # 将两个数据矩阵按行堆叠,得到所有的数据
clamp_data_label = np.zeros((num_label_samples, num_classes), np.float32) # 对于已标记数据的标签矩阵的初始化
for i in range(num_label_samples):
clamp_data_label[i][labels[i]] = 1.0 # 属于哪个类,则哪个类对应的列的位置置为1
label_function = np.zeros((num_samples, num_classes), np.float32) # 初始化总体的F矩阵
label_function[0: num_label_samples][:] = clamp_data_label # 将已标记数据初始化
label_function[num_label_samples:num_samples] = -1 # 将未标记数据的标签随便初始化
affinity_matrix = build_graph_knn(Mat_X, k) # 首先得到P矩阵
iter = 0
pre_label_function = np.zeros((num_samples, num_classes), np.float32) # 每次迭代都会产生预测结果,这个用于记录上一次的label_function
changed = np.abs(pre_label_function - label_function).sum()
while iter < max_iter and changed > tol:
print("---> Iteration %d/%d, changed:%f" % (iter, max_iter, changed))
pre_label_function = label_function
iter += 1
label_function = np.dot(affinity_matrix, label_function) # 按照公式计算
# label_function = np.vstack((clamp_data_label,label_function[num_label_samples]))
label_function[:num_label_samples] = clamp_data_label # 每次都需要将标签数据从新赋为初始的标签,这个是不可以变的
changed = np.abs(pre_label_function - label_function).sum() # 计算迭代前后的一个损失
unlabel_data_labels = np.zeros(num_unlabel_samples) # 初始化未标记数据的预测标签
for i in range(num_unlabel_samples):
unlabel_data_labels[i] = np.argmax(label_function[i + num_label_samples]) # 最终得到的标记矩阵,每一行是该数据属于哪个类的概率分布,取最大的为预测值
return unlabel_data_labels
def show(Mat_Label, labels, Mat_Unlabel, unlabel_data_labels):
for i in range(Mat_Label.shape[0]):
if int(labels[i]) == 0:
plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Dr')
elif int(labels[i]) == 1:
plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Db')
else:
plt.plot(Mat_Label[i, 0], Mat_Label[i, 1], 'Dy')
for i in range(Mat_Unlabel.shape[0]):
if int(unlabel_data_labels[i]) == 0:
plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'or')
elif int(unlabel_data_labels[i]) == 1:
plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'ob')
else:
plt.plot(Mat_Unlabel[i, 0], Mat_Unlabel[i, 1], 'oy')
plt.xlabel('X1')
plt.ylabel('X2')
plt.xlim(0.0, 12.)
plt.ylim(0.0, 12.)
plt.show()
def loadCircleData(num_data):
center = np.array([5.0, 5.0])
radiu_inner = 2
radiu_outer = 4
num_inner = num_data // 3
num_outer = num_data - num_inner
data = []
theta = 0.0
for i in range(num_inner):
pho = (theta % 360) * math.pi / 180
tmp = np.zeros(2, np.float32)
tmp[0] = radiu_inner * math.cos(pho) + np.random.rand(1) + center[0]
tmp[1] = radiu_inner * math.sin(pho) + np.random.rand(1) + center[1]
data.append(tmp)
theta += 2
theta = 0.0
for i in range(num_outer):
pho = (theta % 360) * math.pi / 180
tmp = np.zeros(2, np.float32)
tmp[0] = radiu_outer * math.cos(pho) + np.random.rand(1) + center[0]
tmp[1] = radiu_outer * math.sin(pho) + np.random.rand(1) + center[1]
data.append(tmp)
theta += 1
Mat_Label = np.zeros((2, 2), np.float32)
Mat_Label[0] = center + np.array([-radiu_inner + 0.5, 0])
Mat_Label[1] = center + np.array([-radiu_outer + 0.5, 0])
labels = [0, 1]
Mat_Unlabel = np.vstack(data)
return Mat_Label, labels, Mat_Unlabel
if __name__ == "__main__":
num_unlabel_samples = 800
# Mat_Label, labels, Mat_Unlabel = loadBandData(num_unlabel_samples)
Mat_Label, labels, Mat_Unlabel = loadCircleData(num_unlabel_samples)
unlabel_data_labels = labelPropagation_knn(Mat_Label, Mat_Unlabel, labels, max_iter=300,k=10)
show(Mat_Label, labels, Mat_Unlabel, unlabel_data_labels)
iter=10:
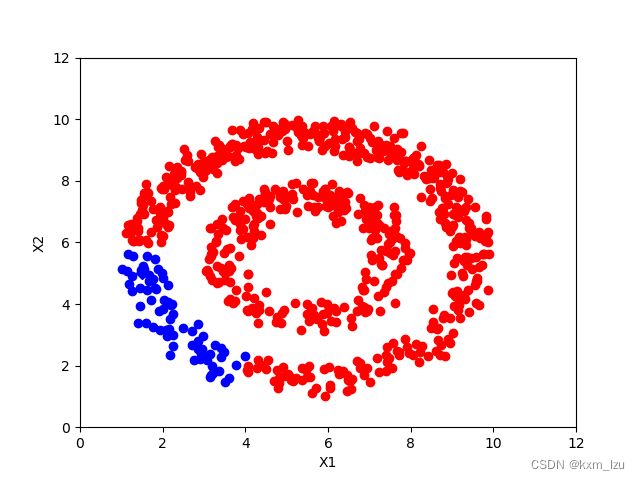
iter=30:
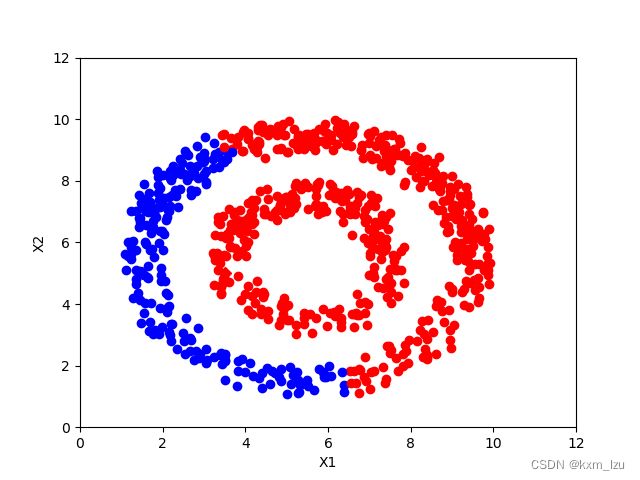
iter=100:
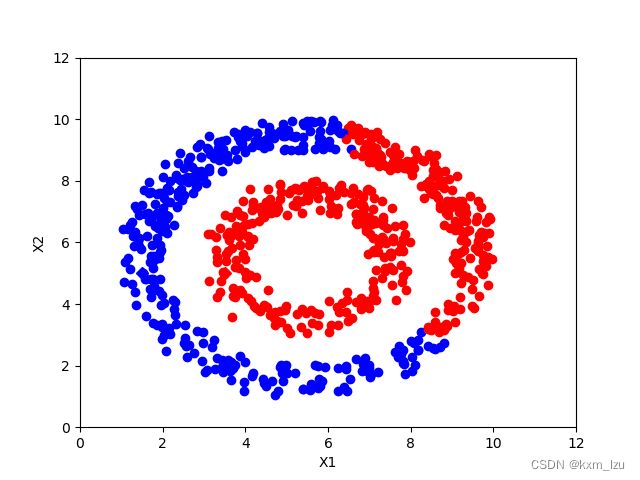
iter=150:
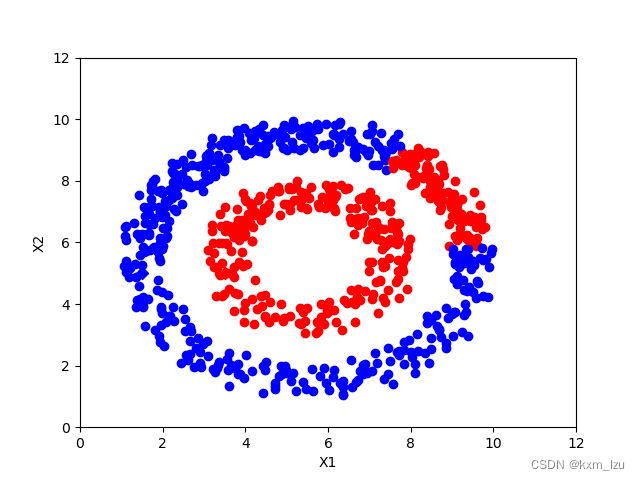
iter=300:

从图中可以清楚的看到传播的过程。
以上是自己在参考相关博客后得出的自己的一些理解,如有错误,还请不吝赐教,谢谢!
参考博客链接:
大佬的博客
