【学习强化学习】十、DDPG、TD3算法原理及实现

参考资料

https://datawhalechina.github.io/easy-rl/#/chapter12/chapter12

代码实现DDPG,TD3，详见github仓库

1. 离散动作 vs. 连续动作

• 离散动作有如下几个例子：
  • 在 CartPole 环境中，可以有向左推小车、向右推小车两个动作。
  • 在 Frozen Lake 环境中，小乌龟可以有上下左右四个动作。
  • 在 Atari 的 Pong 游戏中，游戏有 6 个按键的动作可以输出。
• 但在实际情况中，经常会遇到连续动作空间的情况，也就是输出的动作是不可数的。比如：
  • 推小车力的大小，
  • 选择下一时刻方向盘的转动角度，
  • 四轴飞行器的四个螺旋桨给的电压的大小。

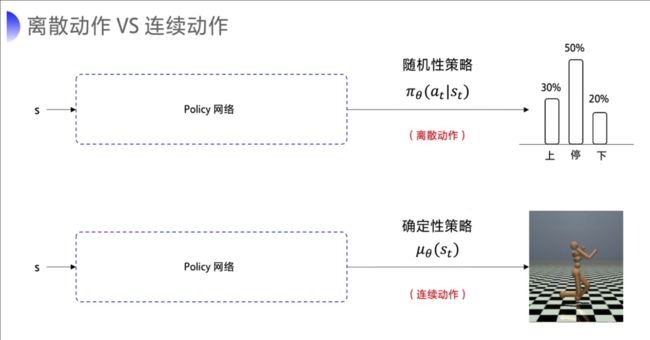
• 在离散动作的场景下，比如说输出上、下或是停止这几个动作。有几个动作，神经网络就输出几个概率值，用${\pi }_{\theta }(a_t|s_t)$来表示这个随机性的策略。

• 在连续的动作场景下，比如说我要输出这个机器人手臂弯曲的角度，我们就输出一个具体的浮点数。我们用 ${\mu }_{\theta }(s_t)$ 来代表这个确定性的策略。

1.1 随机性策略 vs 确定性策略

• 对随机性的策略来说，输入某一个状态 s，采取某一个 action 的可能性并不是百分之百，而是有一个概率 P ，根据概率随机抽取一个动作。
• 对于确定性的策略来说，它没有概率的影响。当神经网络的参数固定下来了之后，输入同样的 state，必然输出同样的 action，这就是确定性的策略。

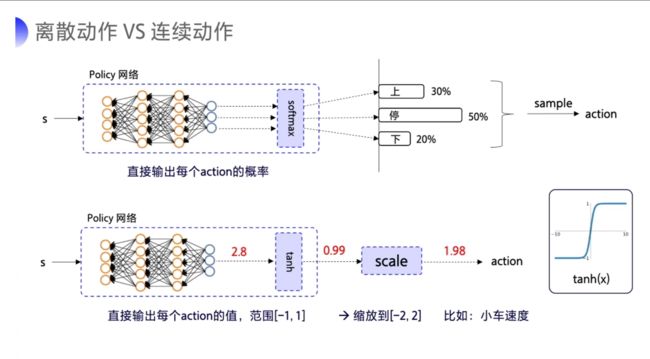
• 要输出离散动作的话，加一层 softmax 层来确保说所有的输出是动作概率，而且所有的动作概率加和为 1。
• 要输出连续动作的话，一般可以在输出层加一层 tanh。
  • tanh 的作用就是把输出限制到 [-1,1] 之间。
  • 我们拿到这个输出后，就可以根据实际动作的范围再做一下缩放，然后再输出给环境。

2. DDPG

2.1 介绍

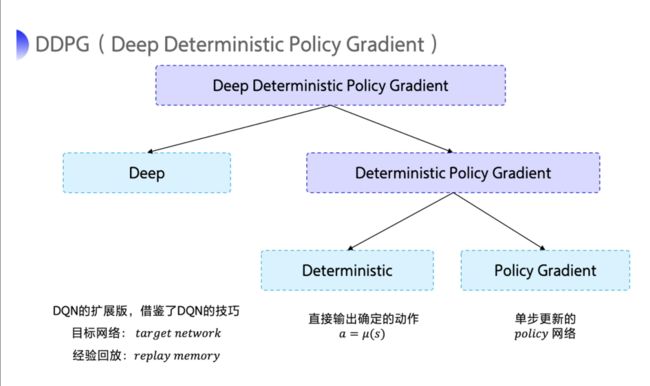
在连续控制领域，比较经典的强化学习算法就是 深度确定性策略梯度(Deep Deterministic Policy Gradient，简称 DDPG)。DDPG 的特点可以从它的名字当中拆解出来，拆解成 Deep、Deterministic 和 Policy Gradient。

• Deep 是因为用了神经网络；

• Deterministic 表示 DDPG 输出的是一个确定性的动作，可以用于连续动作的一个环境；

• Policy Gradient 代表的是它用到的是策略网络。REINFORCE 算法每隔一个 episode 就更新一次，但 DDPG 网络是每个 step 都会更新一次 policy 网络，也就是说它是一个单步更新的 policy 网络。

在深度确定性策略梯度算法中, Actor 是一个确定性策略函数, 表示为 $\pi (s)$, 待学习参数表 示为 ${\theta }^{\pi }$ 。每个动作直接由 $A_t=\pi \left(S_t\mid {\theta }_t^{\pi }\right)$ 计算, 不需要从随机策略中采样。

2.2 DDPG ： DQN 的扩展。

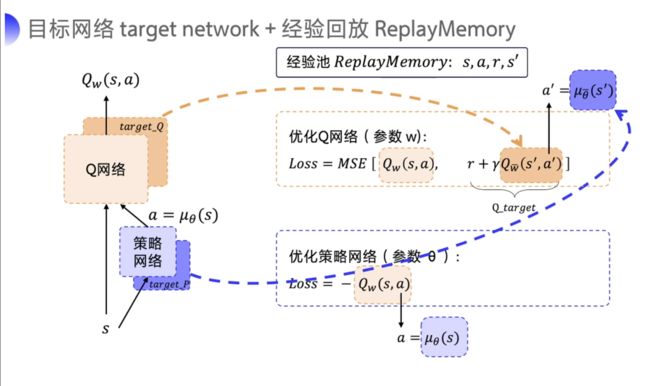
• 在 DDPG 的训练中，它借鉴了 DQN 的技巧：目标网络和经验回放。

• 经验回放这一块跟 DQN 是一样的，但 target network 这一块的更新跟 DQN 有点不一样。

  

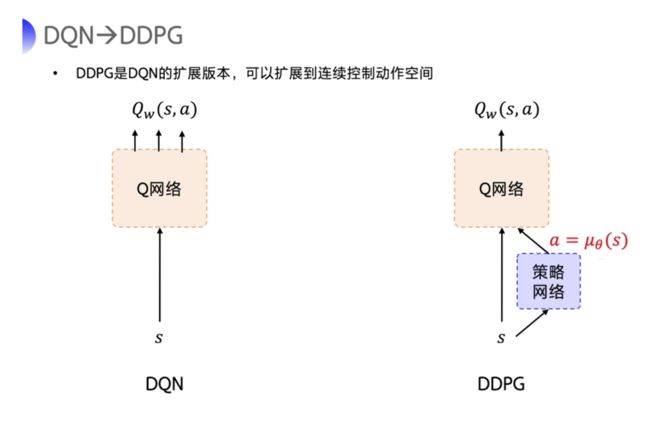
• DDPG 直接在 DQN 基础上加了一个策略网络来直接输出动作值，所以 DDPG 需要一边学习 Q 网络，一边学习策略网络。

• Q 网络的参数用 $w$ 来表示。策略网络的参数用 $\theta$ 来表示。DDPG也为 Actor-Critic 的结构。

接下来就是类似 DQN。

• DQN 的最佳策略是想要学出一个很好的 Q 网络，学好这个网络之后，我们希望选取的那个动作使你的 Q 值最大。

• DDPG 的目的也是为了求解让 Q 值最大的那个 action。

  • Actor 只是为了迎合评委的打分而已，所以用来优化策略网络的梯度就是要最大化这个 Q 值，所以构造的 loss 函数就是让 Q 取一个负号。
  • 我们写代码的时候就是把这个 loss 函数扔到优化器里面，它就会自动最小化 loss，也就是最大化 Q。

这里要注意，除了策略网络要做优化，DDPG 还有一个 Q 网络也要优化。

• 评委一开始也不知道怎么评分，它也是在一步一步的学习当中，慢慢地去给出准确的打分。

• 优化 Q 网络的方法其实跟 DQN 优化 Q 网络的方法一样，我们用真实的 reward r 和下一步的 Q 即 Q’ 来去拟合未来的收益 Q_target。

• 然后让 Q 网络的输出去逼近这个 Q_target。

  • 所以构造的 loss function 就是直接求这两个值的均方差。
  • 构造好 loss 后，通过优化器，让它自动去最小化 loss。

我们可以把两个网络的 loss function 构造出来。

策略网络的 loss function 是一个复合函数。我们把 $a={\mu }_{\theta }(s)$ 代进去，最终策略网络要优化的是策略网络的参数 $\theta$ 。Q 网络要优化的是 $Q_w(s,a)$ 和 Q_target 之间的一个均方差。

但是 Q 网络的优化存在一个和 DQN 一模一样的问题就是它后面的 Q_target 是不稳定的。此外，后面的$Q_{\bar{w}}\left(s^{\prime },a^{\prime }\right)$也是不稳定的，因为 $Q_{\bar{w}}\left(s^{\prime },a^{\prime }\right)$ 也是一个预估的值。

为了稳定这个 Q_target，DDPG 分别给 Q 网络和策略网络都搭建了 target network。

• target_Q 网络就为了来计算 Q_target 里面的 $Q_{\bar{w}}\left(s^{\prime },a^{\prime }\right)$。

• $Q_{\bar{w}}\left(s^{\prime },a^{\prime }\right)$ 里面的需要的 next action $a^{\prime }$ 就是通过 target_P 网络来去输出，即 $a^{\prime }={\mu }_{\bar{\theta }}\left(s^{\prime }\right)$。

• 为了区分前面的 Q 网络和策略网络以及后面的 target_Q 网络和 target_P 策略网络，前面的网络的参数是 $w$，后面的网络的参数是 $\bar{w}$。

• DDPG 有四个网络，策略网络的 target 网络 和 Q 网络的 target 网络，也是固定一段时间的参数之后再跟评估网络同步一下最新的参数。

注意，因为 DDPG 使用了经验回放这个技巧，所以 DDPG 是一个 off-policy 的算法。

这里, 一个关键问题是如何平衡这种确定性策略的探索和利用 (Exploration and Exploitation)。 深度确定性策略梯度算法通过在训练过程中添加随机噪声解决该问题。每个输出动作添加噪声 $N$, 此时有动作为 $A_t=\pi \left(S_t\mid {\theta }_t^{\pi }\right)+N_t$ 。其中 $N$ 可以根据具体任务进行选择, 原论文中使用 Ornstein-Uhlenbeck 过程（O-U 过程）添加噪声项。

2.3 Exploration vs. Exploitation

DDPG 通过 off-policy 的方式来训练一个确定性策略。因为策略是确定的，如果 agent 使用同策略来探索，在一开始的时候，它很可能不会尝试足够多的 action 来找到有用的学习信号。为了让 DDPG 的策略更好地探索，我们在训练的时候给它们的 action 加了噪音。DDPG 的原作者推荐使用时间相关的 OU noise，但最近的结果表明不相关的、均值为 0 的 Gaussian noise 的效果非常好，且后者更简单。为了便于获得更高质量的训练数据，你可以在训练过程中把噪声变小。

在测试的时候，为了查看策略利用它学到的东西的表现，我们不会在 action 中加噪音。

2.4 更新过程

动作价值函数 $Q\left(s,a\mid {\theta }^Q\right)$ 和深度 $\mathrm{Q}$ 网络算法一样, 通过贝尔 曼方程（Bellman Equations）进行更新。

在状态 $S_t$ 下, 通过策略 $\pi$ 执行动作 $A_t=\pi \left(S_t\mid {\theta }_t^{\pi }\right)$, 得到下一个状态 $S_{t+1}$ 和奖励值 $R_t$ 。我 们有 :
$$Q^{\pi }\left(S_t,A_t\right)=\mathbb{E}\left[r\left(S_t,A_t\right)+\gamma Q^{\pi }\left(S_{t+1},\pi \left(S_{t+1}\right)\right)\right]$$
然后计算 $Q$ 值:
$$Y_i=R_i+\gamma Q^{\pi }\left(S_{t+1},\pi \left(S_{t+1}\right)\right)$$
使用梯度下降算法最小化损失函数:
$$L=\frac{1}{N}\sum _i{\left(Y_i-Q\left(S_i,A_i\mid {\theta }^Q\right)\right)}^2.$$

通过将链式法则应用于期望回报函数 $J$ 来更新策略函数 $\pi$ 。这里, $J={\mathbb{E}}_{R_i,S_i\sim E,A_i\sim \pi }\left[R_t\right]$ ( $E$ 表示环境)， $R_t={\sum }_{i=t}^{\mathrm{T}}{\gamma }^{(i-t)}r\left(S_i,A_i\right)$ 。我们有:
$$\begin{array}{rl}{\nabla }_{{\theta }^{\pi }}J& \approx {\mathbb{E}}_{S_t\sim {\rho }^{\beta }}\left[{{\nabla }_{{\theta }^{\pi }}Q\left(s,a\mid {\theta }^Q\right)|}_{s=S_t,a=\pi \left(S_t\mid {\theta }^{\pi }\right)}\right],\\ & ={\mathbb{E}}_{S_t\sim {\rho }^{\beta }}\left[{{{\nabla }_{a}Q\left(s,a\mid {\theta }^Q\right)|}_{s=S_t,a=\pi \left(S_t\right)}{\nabla }_{{\theta }_{\pi }}\pi \left(s\mid {\theta }^{\pi }\right)|}_{s=S_t}\right].\end{array}$$
通过批量样本（Batches）的方式更新:
$${{{\nabla }_{{\theta }^{\pi }}J\approx \frac{1}{N}\sum _i{\nabla }_{a}Q\left(s,a\mid {\theta }^Q\right)|}_{s=S_i,a=\pi \left(S_i\right)}{\nabla }_{{\theta }^{\pi }}\pi \left(s\mid {\theta }^{\pi }\right)|}_{S_i}$$
此外, 深度确定性策略梯度算法采用了类似深度 $\mathrm{Q}$ 网络算法的目标网络, 但这里通过指数平滑方法而不是直接替换参数来更新目标网络:
$$\begin{array}{rl}{\theta }^{Q^{\prime }}& \leftarrow \rho {\theta }^Q+(1-\rho ){\theta }^{Q^{\prime }}\\ {\theta }^{{\pi }^{\prime }}& \leftarrow \rho {\theta }^{\pi }+(1-\rho ){\theta }^{{\pi }^{\prime }}\end{array}$$
由于参数 $\rho \ll 1$, 目标网络的更新缓慢且平稳, 这种方式提高了学习的稳定性。

2.5 伪代码

3. Twin Delayed DDPG(TD3)

3.1 TD3的技巧

虽然 DDPG 有时表现很好，但它在超参数和其他类型的调整方面经常很敏感。DDPG 常见的问题是已经学习好的 Q 函数开始显著地高估 Q 值，然后导致策略被破坏了，因为它利用了 Q 函数中的误差。

双延迟深度确定性策略梯度(Twin Delayed DDPG，简称 TD3)通过引入三个关键技巧来解决这个问题：

• 截断的双 Q 学习(Clipped Dobule Q-learning) 。TD3 学习两个 Q-function（因此名字中有 “twin”）。TD3 通过最小化均方差来同时学习两个 Q-function：$Q_{{\varphi }_1}$​​ 和$Q_{{\varphi }_2}$​​。两个 Q-function 都使用一个目标，两个 Q-function 中给出较小的值会被作为如下的 Q-target：

$$y\left(r,s^{\prime },d\right)=r+\gamma (1-d)\underset{i=1,2}{\min }{Q}_{{\varphi }_{i,targ}}\left(s^{\prime },a_{TD3}\left(s^{\prime }\right)\right)$$

• 延迟的策略更新(“Delayed” Policy Updates) 。相关实验结果表明，同步训练动作网络和评价网络，却不使用目标网络，会导致训练过程不稳定；但是仅固定动作网络时，评价网络往往能够收敛到正确的结果。因此 TD3 算法以较低的频率更新动作网络，较高频率更新评价网络，通常每更新两次评价网络就更新一次策略。
• 目标策略平滑(Target Policy smoothing) 。TD3 引入了 smoothing 的思想。在目标策略的输出动作中加入噪声，以此平滑 Q 值函数的估计，避免过拟合。

目标策略平滑化的工作原理如下：
$$a_{TD3}\left(s^{\prime }\right)=\mathrm{clip}\left({\mu }_{\theta ,targ}\left(s^{\prime }\right)+\mathrm{clip}(ϵ,-c,c),a_{\text{low }},a_{\text{high }}\right)$$
其中 $ϵ$ 本质上是一个噪声，是从正态分布中取样得到的，即 $ϵ\sim N(0,\sigma )$。
目标策略平滑化是一种正则化方法。

3.2 Exploration vs. Exploitation

TD3 以 off-policy 的方式训练确定性策略。由于该策略是确定性的，因此如果智能体要探索策略，则一开始它可能不会尝试采取足够广泛的动作来找到有用的学习信号。为了使 TD3 策略更好地探索，我们在训练时在它们的动作中添加了噪声，通常是不相关的均值为零的高斯噪声。为了便于获取高质量的训练数据，你可以在训练过程中减小噪声的大小。

在测试时，为了查看策略对所学知识的利用程度，我们不会在动作中增加噪音。

3.3 伪代码

4. 练习

4.1 简答

对于连续动作的控制空间和离散动作的控制空间，如果我们都采取使用Policy网络的话，分别应该如何操作？

答：首先需要说明的是，对于连续的动作控制空间，Q-learning、DQN等算法是没有办法处理的，所以我们需要使用神经网络进行处理，因为其可以既输出概率值 ${\pi }_{\theta }(a_t|s_t)$ ，也可以输出确定的策略 ${\mu }_{\theta }(s_t)$ 。
要输出离散动作的话，最后的output的激活函数使用 softmax 就可以实现。其可以保证输出是的动作概率，而且所有的动作概率加和为 1。
要输出连续的动作的话，可以在输出层这里加一层 tanh激活函数。其作用可以把输出限制到 [-1,1] 之间。我们拿到这个输出后，就可以根据实际动作的一个范围再做一下缩放，然后再输出给环境。

DDPG是on-policy还是off-policy，原因是什么？

off-policy。解释方法一，DDPG是优化的DQN，其使用了经验回放，所以为off-policy方法；解释方法二，因为DDPG为了保证一定的探索，对于输出动作加了一定的噪音，也就是说行为策略跟优化的策略不是同一个。

描述D4PG算法呢？

答：分布的分布式DDPG（Distributed Distributional DDPG ，简称 D4PG)，相对于DDPG其优化部分为：

• 分布式 critic: 不再只估计Q值的期望值，而是去估计期望Q值的分布, 即将期望Q值作为一个随机变量来进行估计。
• N步累计回报: 当计算TD误差时，D4PG计算的是N步的TD目标值而不仅仅只有一步，这样就可以考虑未来更多步骤的回报。
• 多个分布式并行actor：D4PG使用K个独立的actor并行收集训练样本并存储到同一个replay buffer中。
• 优先经验回放（Prioritized Experience Replay，PER）：使用一个非均匀概率 $\pi$ 从replay buffer中采样。

4.2 编程题

代码实现DDPG,TD3，详见github仓库