动手学深度学习--4.多层感知机

detach()用法

目的：
神经网络的训练有时候可能希望保持一部分的网络参数不变，只对其中一部分的参数进行调整，或者训练部分分支网络，并不让其梯度对主网络的梯度造成影响，这个时候我妈就需要使用detach()函数来切断一些分支的反向传播。

tensor.detach()

tensor.detach()会返回一个新的tensor，从当前的计算图中分离下来，但是仍指向原变量的存放位置，不同之处只是requires_grad为false, 得到的这个tensor永远不需要计算其梯度，不具有grad。
即使之后重新将它的requires_grad置为true, 它也不会具有梯度grad, 这样我们就会继续使用这个新的tensor进行计算，后面当我们进行反向传播时，到该调用detach()的tensor就会停止，不能再继续向前进行传播。

注意：使用detach返回的tensor和原始的tensor共享一个内存，即一个修改则另一个也会跟着改变

import torch
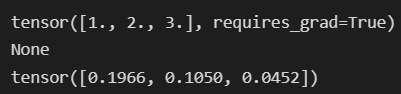
a = torch.tensor([1, 2, 3.], requires_grad=True)
print(a)
print(a.grad)
out = a.sigmoid()
 
out.sum().backward()
print(a.grad)

import torch
a = torch.tensor([1, 2, 3.], requires_grad=True)
print(a.grad)
out = a.sigmoid()
print(out)
 
#添加detach(),c的requires_grad为False
c = out.detach()
print("c--> \t",c)
 
#这时候没有对c进行更改，所以并不会影响backward()
out.sum().backward()
print("a.grad-->",a.grad)

参考博客

backward中的torch.ones_like(x)

y.backward(torch.ones_like(x), retain_graph=True)

因为这里的y是一个向量，x也是向量，向量y对向量x的求导需要
pytorch在求导的过程中，分为下面两种情况：

• 如果是标量对向量求导(scalar对tensor求导)，那么就可以保证上面的计算图的根节点只有一个，此时不用引入grad_tensors参数，直接调用backward函数即可
• 如果是(向量)矩阵对(向量)矩阵求导(tensor对tensor求导)，实际上是先求出Jacobian矩阵中每一个元素的梯度值(每一个元素的梯度值的求解过程对应上面的计算图的求解方法)，然后将这个Jacobian矩阵与grad_tensors参数对应的矩阵进行对应的点乘，得到最终的结果。
  参考博客

nn.CrossEntropyLoss(reduction=‘none’)

reduction = 'none’表示直接返回n分样本的loss，是一个张量
reduction=‘none’)参考博客

模型选择

验证集

原则上，在我们确定所有的超参数之前，我们不希望用到测试集。**如果我们在模型选择过程中使用测试数据，可能会有过拟合测试数据的风险。**所以不能依靠测试数据和训练数据进行模型选择。所以将数据集划分为训练集，测试集，验证集。但测试集和验证集之间的边界模糊，在《动手学深度学习》这本书中两者不做区分。

欠拟合
训练误差和验证误差都很严重，但它们之间仅有一点差距。即模型过于简单，无法捕获试图学习的模式

过拟合
训练误差很小，但是验证误差比较大

synthetic_data函数说明

help(d2l.synthetic_data)

这里也可以用d2l.synthetic_data？或者d2l.synthetic_data？？来查询函数相关信息

如果用两个问号，可以查看函数的具体实现代码

参考博客

权重衰减

已知线性回归的损失函数为：
$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n{l}^{(i)}(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right)}^2.$$
我们希望找到一组参数$({\mathbf{w}}^{\ast },b^{\ast })$这组参数能最小化在所有训练样本上的总损失。如下式：
$${\mathbf{w}}^{\ast },b^{\ast }=\underset{\mathbf{w},b}{\mathrm{argmin}}L(\mathbf{w},b)$$

通过求偏导可以得到解析解为：

$${\mathbf{w}}^{\ast }={\left({\mathbf{X}}^{\mathbf{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y}$$

随机梯度下降法来求解${\mathbf{w}}^{\ast },b^{\ast }$

我们用下面的数学公式来表示这一更新过程（$\partial$ 表示偏导数）：
$$(\mathbf{w},b)\leftarrow (\mathbf{w},b)-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\partial }_{(\mathbf{w},b)}{l}^{(i)}(\mathbf{w},b)$$
总结一下，算法的步骤如下： （1）初始化模型参数的值，如随机初始化； （2）从数据集中随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代这一步骤。 对于平方损失和仿射变换，我们可以明确地写成如下形式:
$$\begin{array}{rl}\mathbf{w}& \leftarrow \mathbf{w}-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\partial }_{\mathbf{w}}{l}^{(i)}(\mathbf{w},b)=\mathbf{w}-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\mathbf{x}}^{(i)}\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right),\\ b\leftarrow b-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\partial }_b{l}^{(i)}(\mathbf{w},b)=b-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right)& \end{array}$$
其中，$\eta$ 表示学习率learning rate, $\mid \mathcal{B}\mid$表示每个小批量中的样本数，这也称为批量大小（batch size）。批量大小和学习率的值通常是手动预先指定，而不是通过模型训练得到的。 这些可以调整但不在训练过程中更新的参数称为超参数

当模型过于复杂的时候会出现过拟合现象，可以用正则化方法来解决过拟合问题。
那如何控制模型的容量呢？
method1: 控制参数的个数
method2:限制参数值的选择范围来控制模型容量$||\mathbf{w}|{|}^2<=\theta$
小的$\theta$意味着更强的正则项

权重衰减∈正则化的一种方式:

$$L(\mathbf{w},b)+\frac{\lambda }{2}\Vert \mathbf{w}{\Vert }^2$$

对于$\lambda =0$，我们恢复了原来的损失函数。 对于$\lambda >0$，我们限制$||\mathbf{w}||$的大小。这里我们仍然除以2：当我们取一个二次函数的导数时， 2和$\frac{1}{2}$会抵消，以确保更新表达式看起来既漂亮又简单.
通过平方$L_2$范数，我们去掉平方根，留下权重向量每个分量的平方和。 这使得惩罚的导数很容易计算：导数的和等于和的导数。

$L_2$正则化回归的小批量随机梯度下降更新如下式：
$$\mathbf{w}\leftarrow (1-\eta \lambda )\mathbf{w}-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\mathbf{x}}^{(i)}\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right)$$

$\lambda$为正则化常数，$\eta$为learning rate

loss.sum().backward()中对于sum()的理解

求和目的：
之前自动求导那节讲到了向量求梯度比较麻烦 都通过sum()转化为标量再求梯度
求和之后后面会除batch_size，可以计算均值

求和本身让 $l$ 以标量的形式表现出来。所有的梯度也叠加了嘛，所以sgd里面除了batch_size
参考博客，这个人的学习笔记写的很好

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

1）with torch.no_grad():
更新时不要计算梯度
2）param.grad.zero_()
pytorch会不断的累加变量的梯度，所以每更新一次参数，就要让其对应的梯度清零
3）for param in params:
对每个参数进行计算（可能是w,可能是b）
4)
不除以batch_size损失函数就是平方和误差
我们只要误差就行了
自动微分

暂退法Dropout

动机：

一个好的模型需要对输入数据的扰动鲁棒

1. 使用有噪音的数据 等价于 Tikhonov正则
2. 丢弃法：在层与层之间加入噪音(即不在输入加噪音，而是在层之间加噪音)

那如何加入这种噪声呢？无偏向的方式注入噪声

一种想法是以一种**无偏向（unbiased）**的方式注入噪声。 这样在固定住其他层时，每一层的期望值等于没有噪音时的值。
将高斯噪声添加到线性模型的输入中。 在每次训练迭代中，他将从均值为零的分布$ϵ\sim \mathcal{N}\left(0,{\sigma }^2\right)$采样噪声添加到输入 $\mathrm{x}$， 从而产生扰动点 ${\mathrm{x}}_{{}^{\prime }}=\mathrm{x}+ϵ$， 预期是 $E[{\mathrm{x}}_{{}^{\prime }}]=\mathrm{x}$。
在标准暂退法正则化中，通过按保留（未丢弃）的节点的分数进行规范化来消除每一层的偏差。 换言之，每个中间活性值以暂退概率由随机变量替换，如下所示：
$$h^{\prime }=\{\begin{array}{ll}0& \text{ 概率为 }p\\ \frac{h}{1-p}& \text{ 其他情况 }\end{array}$$
根据此模型的设计，其期望值保持不变,即 $E[{\mathrm{h}}_{{}^{\prime }}]=\mathrm{h}$。

实现 dropout_layer 函数

从均匀分布中抽取样本，样本数与这层神经网络的维度一致。 实现 dropout_layer 函数， 该函数以dropout的概率丢弃张量输入X中的元素， 如上所述重新缩放剩余部分：将剩余部分除以1.0-dropout(保证了这一层虽然经过dropout操作，但是期望不变)。

import torch
from torch import nn
from d2l import torch as d2l

def dropout_layer(X, dropout):
    assert 0 <= dropout <= 1
    # 在本情况中，所有元素都被丢弃
    if dropout == 1:
        return torch.zeros_like(X)
    # 在本情况中，所有元素都被保留
    if dropout == 0:
        return X
    # torch.rand返回服从[0,1）之间的均匀分布的初始化后的tensor
    print(torch.rand(X.shape))
    mask = (torch.rand(X.shape) > dropout).float()
    return mask * X / (1.0 - dropout)

注意，如果dropout=0.5，那只是说有0.5的概率来决定一个神经元的去留，而不是说这一层一定只有一半的神经元留下