2-1 组合优化问题

1. 组合优化问题

组合数学（Combinatorics）是数学的一个分支，主要研究有限的或者可数的离散结构的存在性、计数和构造问题。

组合优化（也叫离散优化）指在有限个可能解的集合中找出最优解的优化问题。

1.1 组合优化问题定义

首先，我们通过定义对实例和问题做一个区分：

定义1.1（最优化问题的实例） 一个最优化问题的一个实例是一个二元组 $(F,c)$，其中 $F$ 是一个集合，$c$ 是代价函数，从 $F$ 映射到实数集合。要求找出一个 $f\in F$，使得对所有的 $y\in F$，都有 $c(f)\le c(y)$ ，则 $f$ 称为最优解。

定义1.2（最优化问题） 一个最优化问题包含该问题的所有实例。

简单来说，一个实例是给定了输入数据的特定问题，一个问题是所有实例的集合。

定义1.3（组合优化问题） 从一个包含有限对象的集合中，找出一个最优化的对象。

组合优化问题研究的对象是离散的，有限的。

1.2 组合优化问题举例

典型的组合优化问题包括旅行商问题、调度问题、背包问题、装箱问题、最大团问题、聚类问题、图着色问题等。下面我们简单描述一下这些问题，以增强理解。

例1. 旅行商问题（Traveling Salesman Problem, TSP）

给定一个带权无向图 $G=(V,E)$，找出图中一条权值最小的哈密顿回路。哈密顿回路是指从图中某个点出发，经过图中所有节点并回到出发点的路。图中所有顶点必须经过且只能经过一次。

TSP 问题是一个典型的组合优化问题，最优化的对象是权值之和最小的那一个对象。

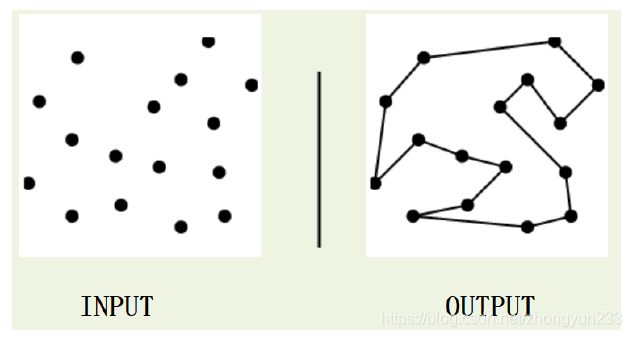
TSP 问题的应用场景有：货物装配、路径规划、订单派送等等。

例2. 最大团问题 (Maximum Clique Problem)

在图 $G=(V,E)$ 中，如果一个顶点的子集 $C$ 中的任意两个顶点都相邻，则称 $C$ 是 $G$ 的一个团。最大团问题即找出 $G$ 中点数最多的团 $C$。
最大团问题可以应用在社交网络（如下图）、蛋白质结构分析等。例如，广告公司投放广告时，如果在几个极大团的交点处投放广告，往往可以节省成本的同时覆盖到更多的用户。

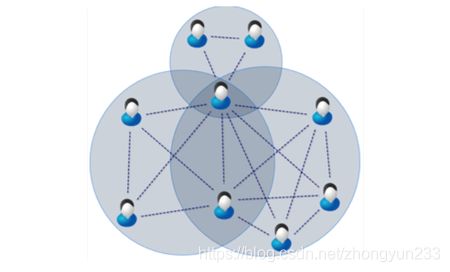
例3. 顶点覆盖问题 (Vertex Cover Problem)

在图 $G=(V,E)$ 中找到一个顶点集合 $L$ ，使得图中任意一条边都至少有一个顶点在 $L$ 中。最小顶点覆盖问题是在 $G$ 中找到最小的 $L$ 集合。

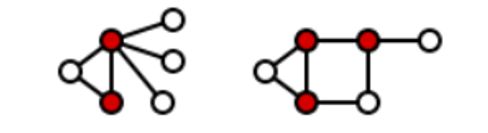
最小顶点覆盖问题常应用于道路监控、网络连接失败的监控分析等等。

例4. 命题逻辑的可满足性问题 (Propositional Satisfiability, SAT)

给定一个命题逻辑公式，判断是否存在一组变量的指派，使得公式为真。
变量的任何一组指派都是该问题的一个对象，因为变量个数有限所以对象也有限，使得命题逻辑得到满足的一组指派是问题的一个最优化对象。

2. 复杂度判定-NP难解问题

为了判定求解一个问题的难度，我们常常通过求解该问题算法的时间复杂度和空间复杂度来描述。

定义2.1（时间复杂度） 设 $A$ 是求解问题 $\omega$ 的算法，用 $A$ 求解 $\omega$ 的实例 $I$ 时，首先把 $I$ 编码为二进制串作为 $A$ 的输入。如果存在函数 $f:N\to N$ ，使得对任意规模为 $n$ 的实例 $I$ ， $A$ 对 $I$ 的运算在 $f(N)$ 内停止，则称算法 $A$ 的时间复杂度为 $f(N)$ 。

以上定义中，问题规模是以二进制编码的长度定义的。
每一个计算步都要有固定常数的执行时间。

2.1 P、NP定义

下面我们从时间复杂度来对不同难度的问题分类。

定义2.2 （判定问题） 判定问题是指答案只有“Yes”和“No”的问题。

判定问题对应一个语言，所有“Yes”的实例构成了这个语言。
一个复杂性类实际上是一个语言集合，该集合中的语言具有相同的属性。

定义2.3 （P-类） 所有多项式时间可解的判定问题组成的问题称作 P 类

定义2.4 （NP-类） 所有非确定性图灵机多项式时间可解的判定问题组成的问题类称为 NP 类。

确定性图灵机对于某个状态会执行确定的指令，而非确定性图灵机则有多条可以执行的指令。
非确定性图灵机是一个不真实的计算模型，可以被其他模型在指数时间下模拟。

如何定义一个问题跟另一个问题一样难？我们引入规约的概念。如果存在一个转换 R，它对每个 B 的输入 x，产生一个 A 的等价输入 R(x)，则称 B 规约到 A 。等价指将 R(x) 作为 A 的输入，得到的回答也是 B 输入 x 的正确回答。

定义2.5（多项式时间规约） 如果有一个确定性图灵机在多项式时间可计算的函数 R，它对于所有输入 x ，$x\in L1$ 当且仅当 $R(x)\in L2$，那么称 L1 规约到 L2 。

有了规约的概念，就可以比较不同问题的难度了。

定义2.6（NP完全问题，NP-compete, NPC） 如果任何一个 NP 问题都可以在多项式时间内规约到该问题，那么该问题为 NPC 问题。

NP 完全概念是针对判定问题而言的，对于组合优化问题，一般采用另一个更一般的概念： NP 难问题。

定义2.7（NP难问题, NP-hard） 求解难度至少和 NPC 问题一样困难的问题。

2.2 SAT问题

SAT 问题是第一个被证明的 NPC 问题。

给定一组可以被赋值为真或假的 n 个变量， $X=\{x_1,x_2,\dots ,x_n\}$，定义文字为变量或者变量的非，如 $l_1=x_1,l_2=\neg x_3$ 。文字的析取组成子句，如 $c_1=x_1\vee x_3\vee \neg x_5$。子句的合取组成合取范式（CNF），如 $F=c_1\wedge c_2\wedge c_3$。

定义2.8（SAT问题） 给定一个CNF公式，判断是否存在一组变量的赋值，使得CNF公式为真，如果为真就返回“SAT”和一组指派，如果不存在则返回“UNSAT”。

绝大多数的组合优化问题都很难求解，一般有以下一些途径来求解：

1. 求解该类问题的子集。
2. 采用近似算法（Approximation algorithms）求出多项式时间的近似解。
3. 采用随机/概率算法(Randomized/Probabilistic algorithms)以一定的概率求得问题的最优解。
4. 采用参数化算法 （Parameterized algorithms），将问题中的某些参数看为常数，固定参数。
5. 采用启发式算法（Heuristic algorithms）。这类算法没有理论保证，经验上往往可以求得很好的解甚至最优解，广泛应用于工程上。