数据结构与算法——栈和队列定义和特点
个人主页:bit..
系列专栏:Linux(Ubuntu)入门必看 C语言刷题 数据结构与算法
目录
一.栈和队
二.栈的定义和特点
三.栈的相关概念
四.栈的相关概念
五.案例引入
5.1 进制转换
5.2括号匹配的检验
5.3表达式求值求值
5.4舞伴问题
一.栈和队
- 栈和队列是两种常见的重要的数据结构
- 栈和队列是限定插入和删除只能在表的“端点”进行的线性表
线性表:
Insert(L,i,x); 1<=i<=n+1
Delete(L,i,x); 1<=i<=n
栈:(后进先出)
Insert(s,n+1,x);
Delete(s,n);
队列:(先进先出)
Insert(Q,n+1,x);
Delete(Q,1);
栈和队列是线性表的子集(是插入和删除位置受限的线性表)
二.栈的定义和特点
栈(stack)
- 是一个特殊的线性表是限定仅在一端(通常是尾部)运行插入和删除操作的线性表
- 又称为先进先出的线性表简称 LIFO 结构 9(Last In First out)
三.栈的相关概念
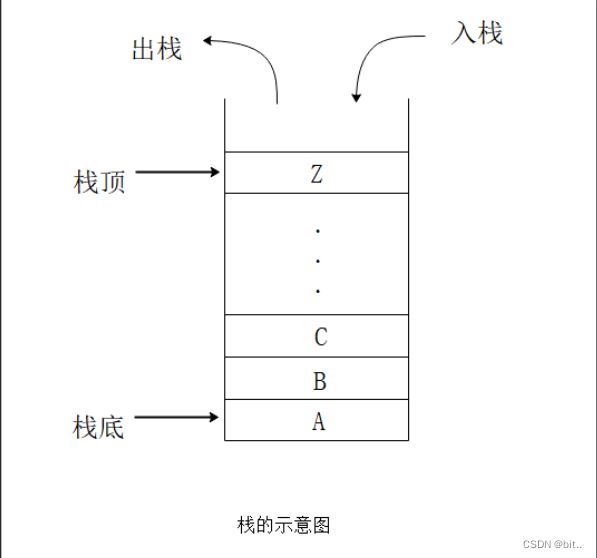
栈是仅有在标尾进行插入,删除操作的线性表,表尾(即an端)又称为栈顶Top,表头a1端为栈底Base
例如:栈 s=(a1,a2,a3,a4,...,an-1,an)
入栈: 插入元素到栈顶(即标尾)的操作
出栈: 从栈顶(即标尾)删除最后一个元素的操作
“入”=压入=PUSH(x)
"出"=弹出=POP(y)
栈的示意图
例如:设a,b,c,入栈顺序为a,b,c,出栈有几种可能
1.c,b,a 2.abc 3.acb 4.bac 5.bca
四.栈的相关概念
1.定义:限定只能在表的一端进行插入和删除运算的线性表(只能在栈顶操作)
2.逻辑结构:与同线性表相同,仍为一对一的关系。
3.存储结构:用顺序栈或链栈存储均可,但以顺序栈更为常见。
4.运算规则:只能在栈顶运算,且访问结点时依照后进先出(LIFO)的原则。
5.实现方式:关键编写入栈和出栈函数,具体实现与顺序栈或链栈的不同而不同。
栈与一般线性表的区别: 仅在运算规则的不同
线性表:随机存储 栈:后进先出(LIFO)
五.队的定义和特点
队列:(queue)
是一种先进先出的线性表,在表的一端插入(标尾),在另一端删除(表头)
队列的相关概念:
定义:只能在表的一端进行插入运算,在表的另一端进行删除运算的线性表(头插尾删)
逻辑结构:同线性表相同,仍为一对一的关系
存储关系:顺序队或链队,以循环顺序队列更常见
运算规则: 只能在队首和队尾运算,且访问结点时依照先进先出的原则
实现方式:关键是掌握入队和出队操作,具体实现依顺序队或链队的不同而不同。
五.案例引入
5.1 进制转换
十进制整数N向其他进制数d(二,八,十六)的转换,是计算机实现计算的基本问题。
转换法则:除以d到取余
该转换法则对应于一个简单算法原理:
n=(n div d)*d+n mod d
div为整除运算 mod为求余运算
#include "Stack.h"
/*s:一个栈对象
n:将要被转换的十进制数
base:进制,若是二进制,则输入 2,若是八进制,则输入 8,以此类推*/
void convert(Stack &s, __int64 n, int base) { //迭代版
//0 < n, 1 < base <= 16,新进制下的数位符号,可视 base 取值范围适当扩充
static char digit[16] = { '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F' };
while (n > 0) { //由低到高,逐一计算出新进制下的各数位
s.push(digit[n % base]);//余数(当前位)入栈
n /= base; //将 n 更新为其对 base 的除商
}
}//新进制下由高到低的各数位,自顶而下保存在栈 s 中 5.2括号匹配的检验
假设表达式中允许包含两种括号:圆括号和方括号
其嵌套的顺序随意,即:
([ ]())或[([ ] [ ])]为正确格式
[(])为错误格式
([())或(()])为错误格式(数量不对)
算法实现:
#define ElemType char
#define MaxSize 50
#include
typedef struct
{
ElemType data[MaxSize];
int top;
}SqStack;
bool StackEmpty(SqStack S)
{
if (S.top == -1) //栈空
return true;
else
return false; //栈不空
}
bool Pop(SqStack& S, ElemType& x)
{
if (S.top == -1) //栈空 不能执行出栈操作
return false;
x = S.data[S.top]; //先出栈 指针再减1
S.top--;
return true;
}
bool Push(SqStack& S, ElemType x)
{
if (S.top == MaxSize - 1) //栈满 不能执行入栈操作
return false;
S.top++; //指针先加1,再入栈
S.data[S.top] = x;
return true;
}
bool GetPop(SqStack S, ElemType& x)
{
if (S.top == -1) //栈空报错
return false;
x = S.data[S.top]; //用x存储栈顶元素
return true;
}
void initStack(SqStack& S)
{
S.top = -1; //初始化栈顶指针
}
int main()
{
SqStack S;
initStack(S);
char sequence[] = { '[','(',')',']','[',']' };
char* p = sequence;
while (*p == '\0')
{
if (*p == '(' || *p=='[')
{
Push(S, *p);
p++;
}
else
{
char getpop;
GetPop(S,getpop);
if ((getpop=='('&&*p==')')||(getpop == '[' && *p == ']')) //判断是否匹配
{
char pop;
Pop(S, pop);
p++;
}
else
{
printf("该序列不合法!");
return 0;
}
}
}
if (StackEmpty(S)) //判断最后栈是否为空
printf("该序列合法!");
else
printf("该序列不合法!");
return 0;
} 5.3表达式求值求值
- 表达式求值是程序设计语言编译中一种最基本的问题,它实现也需要栈
- 这里介绍的算法是由运算符优先级确定运算顺序的对表达式求值算法。
——算符优先算法
- 任何一个算术表达式都是由操作数(常数,变量)
- 算术运算符(+ - × /)和界限符(括号 表达式 结束符 “#”虚设的表达式起始符)组成后两者统称为算符。
为了实现表达式求值需要设置两个栈
- OPTR 用于寄存运算符
- OPND 用于寄存运算数和运算结果
- 求值的处理过程是自左而右扫描表达式的每一个字符
- 当扫描到的是运算数,则将其压入栈OPNG
- 当扫描到的是运算符时 若这个运算符比OPPTR栈顶运算符的优先级高,则入栈OPTR继续向后处理
- 若这个运算符比OPTR栈顶运算符优先级低,则从OPND栈中弹出两个运算数,村栈OPTR中弹出栈顶运算符进行运算,并将运算结果压入栈OPND
- 继续处理当前字符,直到遇到结束符为止
#include
#include
#include
#define MaxSize 100
#define ElemType char
typedef struct{
ElemType data[MaxSize];
int top;
}SqStack;
//顺序栈的初始化:
void InitStack(SqStack &S)
{
memset(S.data,'\0',MaxSize);
S.top=-1;
}
//获取栈顶元素(不是出栈操作!!)
bool GetTop(SqStack &S,ElemType &x)
{
if(S.top==-1)return false;
x=S.data[S.top];
return true;
}
//入栈操作:
bool Push(SqStack &S,ElemType x)
{
if(S.top==(MaxSize-1))return false;
S.data[++S.top]=x;
return true;
}
//出栈操作:
bool Pop(SqStack &S,ElemType &x)
{
if(S.top==-1)return false;
x=S.data[S.top--];
return true;
}
//用于判断运算符优先级的高低,优先级高于或等于就返回true,否则为false
bool Priority(char a,char b)
{
if((a=='+'||a=='-')&&(b=='+'||b=='-'||b=='*'||b=='/'))
{
return true;
}
else if((a=='*'||a=='/')&&(b=='*'||b=='/'))
{
return true;
}
return false;
}
//将中缀表达式转化为后缀表达式:
void ChangeToRPN(ElemType str[],int length,ElemType* &str1) //RPN指逆波兰式,也就是后缀表达式
{
int j=0;
str1=(char*)malloc(sizeof(char)*MaxSize); //str1是字符数组,用于存放处理后的后缀表达式
memset(str1,' ',MaxSize);
ElemType topElem;
SqStack S; //定义一个栈
InitStack(S); //初始化栈
for(int i=0;i='0'&&str[i]<='9') //遇到操作数
{
while(1)
{
str1[j]=str[i];
if(str[i+1]>='0'&&str[i+1]<='9'){
j=j+1;
i++;
}
else{
j=j+2;
break;
}
}
}
else if(str[i]!=')') //遇到运算符或左括号
{
if(str[i]=='(')
{
if(!Push(S,str[i]))printf("Your input is too long!!\n");
continue;
}
else while(GetTop(S,topElem)&&topElem!='('&&Priority(str[i],topElem))
{ //Priority是用于判断运算符优先级的自定义函数
Pop(S,topElem);
str1[j]=topElem;
j=j+2;
}
Push(S,str[i]);
}
else{ //遇到右括号
while(GetTop(S,topElem))
{
Pop(S,topElem);
if(topElem=='(')break;
str1[j]=topElem;
j=j+2;
}
}
}
//将栈中剩下的运算符弹出
while(Pop(S,topElem)){
str1[j]=topElem;
j=j+2;
}
return;
}
int main()
{
char str[50];
char *str1;
memset(str,'\0',50);
printf("\n请输入要转化的中缀表达式:\n");
scanf("%s",str);
ChangeToRPN(str,strlen(str),str1);
printf("\n输出结果:\n");
printf("%s\n",str1);
free(str1);
return 0;
} 5.4舞伴问题
- 首先构造两个队
- 依次将对头元素出队配成舞伴
- 某队为空,则另外一对等待这则是下一个舞曲,第一个可获得舞伴的人
算法描述:
void DancePartner(Person dancer[],int num)
{//结构数组dancer中存放跳舞的男女,num是跳舞的人数。
InitQueue(Mdancers); //男士队列初始化
InitQueue(Fdancers); //女士队列初始化
for(i=0;i