自动控制原理学习--奈奎斯特稳定判据
一、重点知识点汇总
1.幅角原理
对于复变函数
函数![]() 是复变量s的单值函数,s可以在整个s平面上变化,对于其上的每一点,除n个有限极点外,函数
是复变量s的单值函数,s可以在整个s平面上变化,对于其上的每一点,除n个有限极点外,函数![]() 都有唯一的一个值与之对应。
都有唯一的一个值与之对应。![]() 的值域,也构成一个F(s)的复平面。s平面上的每一点,除极点之外,依照所给的函数关系,都将映射到
的值域,也构成一个F(s)的复平面。s平面上的每一点,除极点之外,依照所给的函数关系,都将映射到![]() 平面上的响应点。其中s平面上的全部零点都将映射到
平面上的响应点。其中s平面上的全部零点都将映射到![]() 平面上的原点;s平面上的极点都会映射到
平面上的原点;s平面上的极点都会映射到![]() 平面上的无限远点;其余s平面的普通点,都将映射到
平面上的无限远点;其余s平面的普通点,都将映射到![]() 的有限非零点。
的有限非零点。
奈奎斯特路径依据:s平面上既不经过![]() 零点也不经过
零点也不经过![]() 极点的一条封闭曲线
极点的一条封闭曲线![]() 。当s沿
。当s沿![]() 顺时针方向绕行一周,连续取值时,则会在
顺时针方向绕行一周,连续取值时,则会在![]() 平面上映射出一条封闭曲线
平面上映射出一条封闭曲线![]() 。在这种映射关系中,不需知道围线
。在这种映射关系中,不需知道围线![]() 的确切形状和位置,只要知道它的內域所包含的
的确切形状和位置,只要知道它的內域所包含的![]() 的零点和极点的数目,就可以预知映射
的零点和极点的数目,就可以预知映射![]() 是否包围坐标原点,以及包围原点的次数。
是否包围坐标原点,以及包围原点的次数。
幅角原理:如果围线![]() 包围
包围![]() 的Z个零点和P个极点,那么,当s沿
的Z个零点和P个极点,那么,当s沿![]() 顺时针绕行一周时,
顺时针绕行一周时,![]() 应顺时针包围Z−P次。亦即
应顺时针包围Z−P次。亦即![]() 顺时针包围原点次数N=Z−P。
顺时针包围原点次数N=Z−P。
P.S.实际上奈奎斯特稳定判据的核心就是这个N=Z−P,之后的公式无论怎么变,都其实左右移项的结果。然后这个公式的记忆可以和前面的对数坐标联系起来,位于位于分子位置上的零点在顺时针的绕行的情况下提供正相位,位于分母位置上的极点提供负相位,最后得到的相位差就是包围零点的度数。
2.奈奎斯特稳定判据
有理分式F(s)的选取:对于一个负反馈系统而言,前向通路传递函数为![]() ,反馈函数为
,反馈函数为![]() ,则开环传递函数为
,则开环传递函数为
闭环传递函数为
![]()
再令![]() ,
,![]() 和
和![]() 分别为开环和闭环系统的特征多项式,现以它们之比构成
分别为开环和闭环系统的特征多项式,现以它们之比构成![]() ,有
,有
即![]() 为开环传递函数加1,由此可知
为开环传递函数加1,由此可知![]() 的零点是闭环传递函数的极点,
的零点是闭环传递函数的极点,![]() 的极点是开环传递函数的极点。
的极点是开环传递函数的极点。
P.S.其实这是一个十分天才也十分巧妙的构造,因为对于一个系统而言,其闭环传递函数的极点是判断系统稳定性的关键,但是闭环极点相比开环极点往往不易求得,而且对于判断系统稳定性而言,只需判断闭环极点是否会出现在有半平面,而不关心其确切位置。通过这样的方法构造的![]() 函数将开环极点和闭环极点联系起来,并通过选择一条特殊的奈奎斯特路径,根据幅角原理判断闭环系统稳定性。
函数将开环极点和闭环极点联系起来,并通过选择一条特殊的奈奎斯特路径,根据幅角原理判断闭环系统稳定性。
已知闭环系统稳定的充要条件是闭环特征方程的全部特征跟的实部为负。确定目标问题:在已知F(s)的极点位置时,判断![]() 在右半平面有无零点的问题。
在右半平面有无零点的问题。
常规奈奎斯特路径选择:
- 正虚轴:
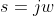 ,频率w由0变化到
,频率w由0变化到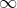 ;
; - 半径为无穷大的右半圆:
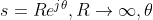 由
由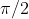 变化到
变化到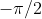 ;
; - 负虚轴:
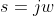 ,频率w由
,频率w由 变化到0;
变化到0;
特殊奈奎斯特路径选择:
当系统开环传递函数在虚轴上存在极点时,即有开环极点![]() 或
或![]() 。为满足幅角原理的条件,应用半径为无穷小的半圆从右边绕过虚轴上的极点,从而把虚轴上的极点看作是左极点。当然也可以用半径为无穷小的半圆从左边绕过虚轴上的极点,从而把虚轴上的极点看作是右极点。
。为满足幅角原理的条件,应用半径为无穷小的半圆从右边绕过虚轴上的极点,从而把虚轴上的极点看作是左极点。当然也可以用半径为无穷小的半圆从左边绕过虚轴上的极点,从而把虚轴上的极点看作是右极点。
当系统开环传递函数在原点处有v个极点时,无穷小右半圆在![]() 平面的映射是连接
平面的映射是连接![]() 和
和![]() 从
从![]() 到
到![]() 顺时针转过
顺时针转过![]() 的无穷大圆弧;若选用无穷小左半圆,则它在Gk(s)平面的映射是连接
的无穷大圆弧;若选用无穷小左半圆,则它在Gk(s)平面的映射是连接![]() 和
和![]() 从
从![]() 到
到![]() 逆时针转过
逆时针转过![]() 。当系统开环传递函数在虚轴上存在极点
。当系统开环传递函数在虚轴上存在极点![]() ,无穷小半圆在
,无穷小半圆在![]() 平面的映射是类似的。
平面的映射是类似的。
奈奎斯特稳定判据:
由于![]() 在
在![]() 平面上沿着封闭曲线
平面上沿着封闭曲线![]() 包围原点的次数正好对应于
包围原点的次数正好对应于![]() 平面上的封闭曲线
平面上的封闭曲线![]() 包围
包围![]() 点的次数。
点的次数。
反馈控制系统闭环极点在s右半平面的个数为
![]()
式中,P为系统开环传递函数在s右半平面的极点个数;N为开环极坐标图及其镜像(![]() )顺时针包围
)顺时针包围![]() 点的圈数。若
点的圈数。若![]() ,则闭环系统稳定;若
,则闭环系统稳定;若![]() ,则闭环系统不稳定。
,则闭环系统不稳定。
应注意以下几点:
- 判据中的s的右半平面是指右半开平面,不包括虚轴
- 所谓顺时针包围
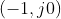 的圈数N是极坐标图及其镜像顺时针包围
的圈数N是极坐标图及其镜像顺时针包围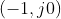 点圈数和逆时针包围
点圈数和逆时针包围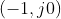 点圈数的代数和,当
点圈数的代数和,当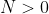 时表示顺时针包围
时表示顺时针包围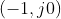 点,当
点,当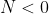 时表示逆时针包围
时表示逆时针包围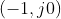 点
点 - Z一定要大于等于0,若求出
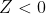 ,则一定计算有误
,则一定计算有误 - 若开环极坐标图正好通过
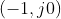 点,则闭环系统存在虚轴上的极点,即
点,则闭环系统存在虚轴上的极点,即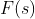 在虚轴上存在零点,此时不满足幅角原理的条件,N值就变成不确定的,奈奎斯特判据也就不能直接应用。闭环特征多项式有简单的虚根,工程上认为这种情况是不稳定的
在虚轴上存在零点,此时不满足幅角原理的条件,N值就变成不确定的,奈奎斯特判据也就不能直接应用。闭环特征多项式有简单的虚根,工程上认为这种情况是不稳定的 - 上述奈奎斯特判据是在假设开环传递函数中不存在零点、极点相消的前提下进行的。如果开环传递函数中存在零点、极点相消,那么,只有被消去的极点具有负实部,且应用奈奎斯特判据判定闭环系统稳定时,闭环系统才稳定
- 奈奎斯特稳定判据还可用于开环传递函数零点、极点位置的判断。此时要考察完整的奈奎斯特曲线对
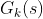 平面原点的包围次数(即要考察包括半径为无穷大右半圆那一段在内的所有奈奎斯特路径在
平面原点的包围次数(即要考察包括半径为无穷大右半圆那一段在内的所有奈奎斯特路径在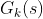 平面的映射对原点的包围次数)
平面的映射对原点的包围次数)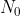 。在这种情况下
。在这种情况下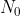 和开环右零点数
和开环右零点数 之间满足下列关系
之间满足下列关系 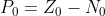
- 频率特性对
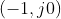 点的包围情况可以用频率特性曲线的正、负穿越来讨论。当w增加时(w从
点的包围情况可以用频率特性曲线的正、负穿越来讨论。当w增加时(w从 到
到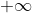 ),频率特性曲线自上而下穿过-1以左的负实轴(相角增加)称为正穿越,穿过一次,穿越数
),频率特性曲线自上而下穿过-1以左的负实轴(相角增加)称为正穿越,穿过一次,穿越数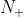 为1;反之频率特性曲线自下而上穿过-1以左的负实轴(相角减少)称为负穿越,穿过一次,穿越数
为1;反之频率特性曲线自下而上穿过-1以左的负实轴(相角减少)称为负穿越,穿过一次,穿越数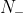 为1。于是,
为1。于是,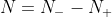 。当只画正频率部分的频率特性时,所得正负穿越分别用
。当只画正频率部分的频率特性时,所得正负穿越分别用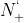 和
和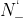 表示,这时若有从-1以左的负实轴开始向上(或向下)的穿越0.5次负穿越(或正穿越)。于是
表示,这时若有从-1以左的负实轴开始向上(或向下)的穿越0.5次负穿越(或正穿越)。于是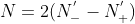
二、精选例题讲解
例1:已知单位反馈控制系统的开环传递函数为
![]()
(1)用奈奎斯特判据确定使闭环系统稳定的条件
(2)用奈奎斯特判据确定使全部闭环极点均位于s平面左半部且实部的绝对值都大于1的条件
解:
(1)此题给出的是I型系统,取特殊奈奎斯特路径,即奈奎斯特路径选取由以下各段组成的s平面上的封闭曲线:
1.正虚轴:![]() ,频率w由
,频率w由![]() 变化到
变化到![]() ;
;
2.半径为无穷大的右半圆:![]() 由
由![]() 变化到
变化到![]() ;
;
3.负虚轴:![]() ,频率w由
,频率w由![]() 变化到
变化到![]() ;
;
4.半径为无穷小的右半圆:![]() 由
由![]() 变化到
变化到![]() ;
;
先求与路径1对应的奈奎斯特图,将![]() 代入
代入![]() ,得
,得
求与实轴的交点,令![]() ,解得
,解得
![]()
与路径2对应的奈奎斯特图是半径为无穷小,角度从![]() 逆时针转到
逆时针转到![]() 的圆弧,由于此段奈奎斯特图与奈奎斯特稳定判据应用到闭环系统判稳无关,所以在画图时可以不画。
的圆弧,由于此段奈奎斯特图与奈奎斯特稳定判据应用到闭环系统判稳无关,所以在画图时可以不画。
与路径3对应的奈奎斯特图是路径1对应的奈奎斯特图关于实轴的镜像。
与路径4对应的奈奎斯特图是半径为无穷大,角度从![]() 顺时针转到
顺时针转到![]() 的圆弧。
的圆弧。
画出奈奎斯特图应如图所示,此时![]() ,要使闭环系统稳定,要求
,要使闭环系统稳定,要求![]() ,即当
,即当![]() 时闭环系统稳定。
时闭环系统稳定。
(2)此时取奈奎斯特路径如图所示,即奈奎斯特路径选取了由以下各段组成的s平面上的封闭曲线:
1.正虚轴:![]() ,频率w由0变化到
,频率w由0变化到![]() ;
;
2.半径为无穷大的右半圆:![]() 由
由![]() 变化到
变化到![]() ;
;
3.负虚轴:![]() ,频率w由
,频率w由![]() 变化到0;
变化到0;
先求与路径1对应的奈奎斯特图
将![]() 代入
代入![]() ,得
,得
![]()
注意此时的![]() 已不是I型系统形式,而是具有一个开环右极点的非最小相位传递函数。对应有
已不是I型系统形式,而是具有一个开环右极点的非最小相位传递函数。对应有
画出奈奎斯特图如图所示。
与路径2对应的奈奎斯特图是半径为无穷小,角度从![]() 逆时针转到
逆时针转到![]() 的圆弧,由于此段奈奎斯特图与奈奎斯特稳定判据应用到闭环系统判稳无关,所以在画图时可以不画。
的圆弧,由于此段奈奎斯特图与奈奎斯特稳定判据应用到闭环系统判稳无关,所以在画图时可以不画。
与路径3对应的奈奎斯特图是路径1对应的奈奎斯特图关于实轴的镜像。
此时![]() ,只有
,只有![]() 才能满足稳定的要求,于是有
才能满足稳定的要求,于是有![]() ,即当
,即当![]() 时满足全部闭环极点均位于s平面左半部且实部的绝对值都大于1的条件。
时满足全部闭环极点均位于s平面左半部且实部的绝对值都大于1的条件。
作为对比,本题的结果也可利用劳斯判据来获得,方法是平移坐标轴后再用劳斯判据判断相对稳定条件。令![]() 代入特征方程
代入特征方程
![]()
整理得![]()
列劳斯阵列如下
要使劳斯阵列第一列都大于零,可解得![]() 。即当
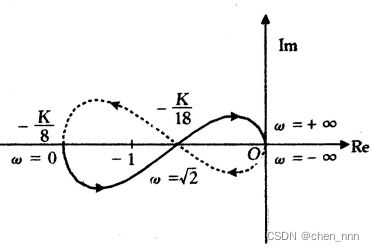
。即当![]() 时满足全部闭环极点均位于s平面左半部且实部的绝对值都大于1是的条件,此结果与应用奈奎斯特判据所得结果完全相同。 例2:图是开环传递函数为G(s)的单位反馈控制系统的奈奎斯特图,确定在下列各种条件下系统的开环传递函数和闭环传递函数在右半平面的极点数,并确定系统的开环稳定性和闭环稳定性。
时满足全部闭环极点均位于s平面左半部且实部的绝对值都大于1是的条件,此结果与应用奈奎斯特判据所得结果完全相同。 例2:图是开环传递函数为G(s)的单位反馈控制系统的奈奎斯特图,确定在下列各种条件下系统的开环传递函数和闭环传递函数在右半平面的极点数,并确定系统的开环稳定性和闭环稳定性。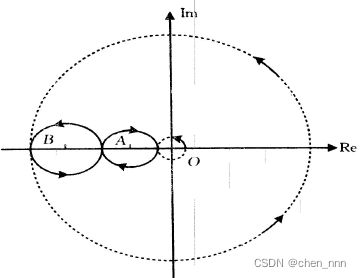
(1)![]() 在右半s平面有一个零点;
在右半s平面有一个零点;![]() 点位于点A。
点位于点A。
(2)![]() 在右半s平面有一个零点;
在右半s平面有一个零点;![]() 点位于点B。
点位于点B。
(3)![]() 在右半s平面有没有零点;
在右半s平面有没有零点;![]() 点位于点A。
点位于点A。
(4)![]() 在右半s平面有没有零点;
在右半s平面有没有零点;![]() 点位于点B。
点位于点B。
解:本题的解题步骤是:1.在已知开环传递函数在右半平面的零点数Z0,及完整的奈奎斯特图对原点的包围圈数N0的情况下,根据奈奎斯特判据确定开环传递函数在右半平面的极点数P0。2.在已知开环传递函数在右半平面的极点数P,及完整的奈奎斯特图对(−1,j0)点的包围圈数N的情况下,根据奈奎斯特判据确定闭环传递函数在右半平面的极点数Z。
(1)已知![]() (奈奎斯特图逆时针包围原点两圈),所以
(奈奎斯特图逆时针包围原点两圈),所以![]() ,开环系统有3个右极点,开环系统不稳定。又知
,开环系统有3个右极点,开环系统不稳定。又知![]() (奈奎斯特图顺时针和逆时针各包围(
(奈奎斯特图顺时针和逆时针各包围(![]() 点一圈,净包围
点一圈,净包围![]() 点零圈),
点零圈),![]() ,闭环不稳定。闭环系统有3个右极点。
,闭环不稳定。闭环系统有3个右极点。
(2)已知![]() ,所以
,所以![]() ,开环系统有3个右极点,开环系统不稳定。又知
,开环系统有3个右极点,开环系统不稳定。又知![]() (奈奎斯特图逆时针包围
(奈奎斯特图逆时针包围![]() 点两圈),
点两圈),![]() ,闭环不稳定。闭环系统有1个右极点。
,闭环不稳定。闭环系统有1个右极点。
(3)已知![]() ,所以
,所以![]() ,开环系统有2个右极点,开环系统不稳定。又知
,开环系统有2个右极点,开环系统不稳定。又知![]() ,闭环不稳定。闭环系统有2个右极点。
,闭环不稳定。闭环系统有2个右极点。
(4)已知![]() ,所以
,所以![]() ,开环系统有2个右极点,开环系统不稳定。又知
,开环系统有2个右极点,开环系统不稳定。又知![]() ,闭环系统稳定。
,闭环系统稳定。
三、备考建议
奈奎斯特稳定判据是重点和难点内容,在复习过程中忌讳眼高手低,一定要多找练习题去自己动手做一遍,在做题中间遇到的各种问题返回到书中对应位置反复咀嚼,多重复多练习,见多识广,在考试过程中才不会慌张。