机器学习—线性回归模型

线性模型

# 用sklearn线性模型
from sklearn.linear_model import LinearRegression
# 实例化对象
lin_reg = LinearRegression() 
# 训练
lin_reg.fit(X,y)
# 输出偏置项
print(lin_reg.intercept_)
# 输出权重项
print(lin_reg.coef_)
'''
[4.61793367]
[[2.90962574]]
'''

批量梯度下降

eta = 0.1 # 学习率
n_iterations = 1000 # 迭代次数
m = 100 # 样本个数
# 随机初始化
theta = np.random.randn(2,1) 
# 迭代梯度下降
for n_iterations in range(n_iterations):
    gradients = 2/m*X_b.T.dot((X_b.dot(theta)-y)) # 梯度下降公式
    theta = theta - eta*gradients   # 更新

• 学习率对结果的影响

  学习率应当尽可能小，随着迭代的进行应当越来越小。

theta_path_bgd = []
# 画图：学习率不同的梯度下降
def plot_gradient_descent(theta,eta,theta_path = None):
    m = len(X_b) # 样本个数
    plt.plot(X,y,'b.') # 原始数据画图
    n_iterations = 1000 # 迭代次数
    # 批量梯度下降
    for n_iterations in range(n_iterations):
        y_predict = X_new_b.dot(theta) # 预测值，x*θ=y
        # 画图：预测值
        plt.plot(X_new,y_predict,'b-')
        gradients = 2/m*X_b.T.dot((X_b.dot(theta)-y)) # 梯度下降公式
        theta = theta - eta*gradients   # 更新
        # 存储theta
        if theta_path is not None:
            theta_path.append(theta)
    plt.xlabel('X_1')
    plt.axis([0,2,0,15])
    plt.title('eta = {}'.format(eta))

theta = np.random.rand(2,1) # 随机初始化
plt.figure(figsize = (10,4))
# 构造1行3列画板，在第1个位置画图
plt.subplot(131)
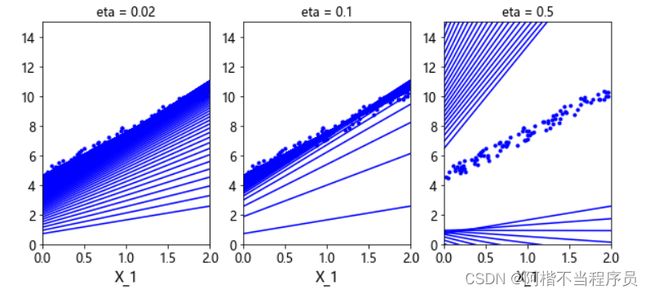
plot_gradient_descent(theta,eta = 0.02)

plt.subplot(132)
plot_gradient_descent(theta,eta = 0.1)

plt.subplot(133)
plot_gradient_descent(theta,eta = 0.5)

由图可知，学习率较小时，迭代次数增多；较大时，可能会略过最佳位置。

随机梯度下降

theta_path_sgd = []
m = len(X_b) # 样本个数
n_epochs = 50 # 迭代次数

t0 = 5
t1 = 50
# 衰减策略
def learning_schedule(t):
    return t0/(t1+t) # 分母越来越大，数值越来越小

theta = np.random.rand(2,1)

# 让所有样本迭代n_epochs次
for epochs in range(n_epochs):
    for i in range(m):
        # 画图：前10次epochs，前10个样本
        if epochs < 10  and i < 10:
            y_predict = X_new_b.dot(theta)
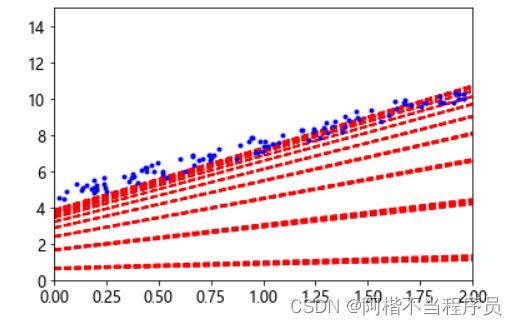
            plt.plot(X_new,y_predict,'r--')
        random_index = np.random.randint(m) # 从1~m中获得一个随机值
        xi = X_b[random_index:random_index+1] # 取出当前随机索引所对应的数据
        yi = y[random_index:random_index+1]
        gradients = 2 * xi.T.dot(xi.dot(theta)-yi)
        # 学习率衰减
        eta = learning_schedule(n_epochs * m+i)
        theta = theta - eta*gradients # 更新
        theta_path_sgd.append(theta) # 存储tehta值
plt.plot(X,y,'b.')
plt.axis([0,2,0,15])
plt.show()

由图，随着迭代次数，会越来越拟合数据，且每次运行时结果都不完全一致，这就是随机性。

MiniBatch梯度下降

指定每次迭代的样本个数，一般为8,16,32,64,256…；

一般情况下，batch数量应当越大越好。

theta_path_mgd = []
n_epochs = 50
n_iteritions = 50
minibatch = 16
theta = np.random.randn(2,1)
np.random.seed(0) # 随机种子，使每次生成的随机数都相同

t = 0 # 计数
for epochs in range(n_epochs):
    shuffled_indices = np.random.permutation(m) # 洗牌,打乱索引
    X_b_shuffled = X_b[shuffled_indices]
    y_shuffled = y[shuffled_indices]
    for i in range(0,m,minibatch): # 从0开始，每次取16个样本
        t+=1
        xi = X_b_shuffled[i:i+minibatch] # 取当前指定的一组样本
        yi = y_shuffled[i:i+minibatch]
        gradients = 2/minibatch*X_b.T.dot((X_b.dot(theta)-y)) # 梯度下降公式
        # 学习率衰减
        eta = learning_schedule(t)
        theta = theta - eta*gradients # 更新
        theta_path_mgd.append(theta) # 存储tehta值

>> theta
array([[4.61793367],
       [2.90962574]])

三种策略对比

# 将theta数组转为ndarray类型
theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)

# 画图
plt.figure(figsize=(12,6))
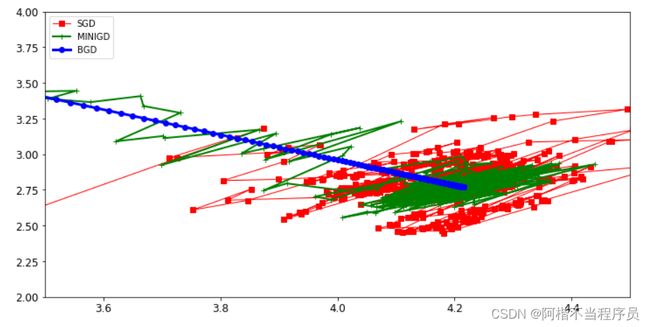
plt.plot(theta_path_sgd[:,0],theta_path_sgd[:,1],'r-s',linewidth=1,label='SGD')
plt.plot(theta_path_mgd[:,0],theta_path_mgd[:,1],'g-+',linewidth=2,label='MINIGD')
plt.plot(theta_path_bgd[:,0],theta_path_bgd[:,1],'b-o',linewidth=3,label='BGD')
plt.legend(loc='upper left')
plt.axis([3.5,4.5,2.0,4.0])
plt.show()

BGD批量梯度下降：直接朝着正确方向走，但样本量较大时，非常耗时。

MINIGD小批量梯度下降：由于样本有限，行走路线有起伏。

• 实际当中用minibatch比较多，一般情况下选择batch数量应当越大越好。

SGD随机梯度下降：随机性较大，可能会趋近于正确路线。

多项式回归

• 出现高次幂时，需要用曲线拟合

# 数据准备
m = 100
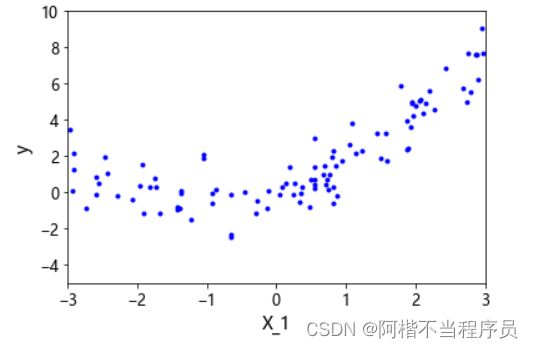
X = 6*np.random.rand(m,1) - 3 # 样本范围为（-3,3）
y = 0.5 * X**2 + X + np.random.randn(m,1)

# 画图
plt.plot(X,y,'b.')
plt.xlabel('X_1')
plt.ylabel('y')
plt.axis([-3,3,-5,10])
plt.show()

# 导入多项式函数
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree = 2,include_bias = False) # 实例化，最高次为2，无偏置项

X_poly = poly_features.fit_transform(X) # 拟合数据，构造特征并返回
X[0]
# array([0.03664337])
X_poly[0] # [x,x^2]
# array([0.03664337, 0.00134274])

在X_poly中，构造出了$x^2$的特征。

# 线性回归模型
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_poly,y)
print(lin_reg.coef_)
print(lin_reg.intercept_)
'''
[[1.04138111 0.52292947]]
[0.03953664]
'''

得到回归方程：$y=1.04x+0.52x^2+0.039$

• 不同degree(幂次)值的效果

# 管道，标准化
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
plt.figure(figsize=(12,6))
# 三种degree值
for style,width,degree in (('g-',1,50),('y-',1,2),('r-',1,1)):
    poly_features = PolynomialFeatures(degree = degree,include_bias = False)
    std = StandardScaler() 
    lin_reg = LinearRegression()
    # 建立管道：构造特征 --> 标准化 --> 建模
    polynomial_reg = Pipeline([('poly_features',poly_features),
              ('StandardScaler',std),
              ('lin_reg',lin_reg)
    ])
    polynomial_reg.fit(X,y)  # 训练
    y_test_2 = polynomial_reg.predict(X_test)  # 获得预测值
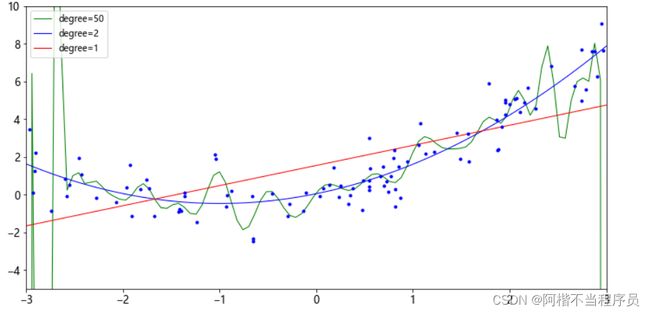
    plt.plot(X_test,y_test_2,style,label = 'degree='+str(degree),linewidth = width)
plt.plot(X,y,'b.') # 原始数据
plt.legend(loc='upper left')
plt.axis([-3,3,-5,10])
plt.show()

degree较大时，会尽量的满足所有点，造成过拟合，在训练集上效果还不错，但在测试集上就学得太过了。

特征变换的越复杂，得到的结果过拟合风险越高，不建议做得特别复杂。

数据样本数量对结果的影响

# 均方误差
from sklearn.metrics import mean_squared_error
# 训练集与测试集切分
from sklearn.model_selection import train_test_split

def polt_learning_curves(model,X,y):
    # 切分，训练集0.8，测试集0.2，指定种子使随机结果相同
    X_train, X_val, y_train, y_val = train_test_split(X,y,test_size = 0.2,random_state=0) 
    # 均方误差
    train_errors,val_errors = [],[]
    # 基于不同样本数量进行训练
    for m in range(1,len(X_train)):
        model.fit(X_train[:m],y_train[:m])
        y_train_predict = model.predict(X_train[:m]) # 训练集预测值
        y_val_predict = model.predict(X_val) # 验证集预测值
        # 均方误差是传入真实值，预测值
        train_errors.append(mean_squared_error(y_train[:m],y_train_predict[:m]))
        val_errors.append(mean_squared_error(y_val,y_val_predict))
    # 均方根误差
    plt.plot(np.sqrt(train_errors),'r-',linewidth = 1,label='train_error')
    plt.plot(np.sqrt(val_errors),'b-',linewidth = 1,label='val_errors')
    plt.xlabel('Trainsing set size')
    plt.ylabel('RMSE')
    plt.legend()

lin_reg = LinearRegression()
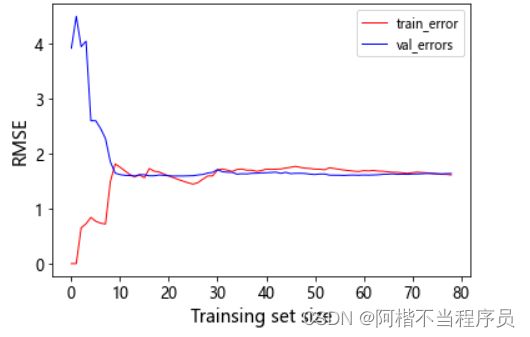
polt_learning_curves(lin_reg,X,y)
plt.show()

数据样本较小时，训练集的rmse低（好），测试集高（不好），即训练集和测试集的误差大，过拟合风险大。

数据样本增加时，训练集与测试集的误差越来越小。

• 多项式回归的过拟合风险

# 建立管道：构造特征 --> 线性模型
polynomial_reg = Pipeline([('poly_features',PolynomialFeatures(degree=10,include_bias=False)),
                           ('lin_reg',LinearRegression())])
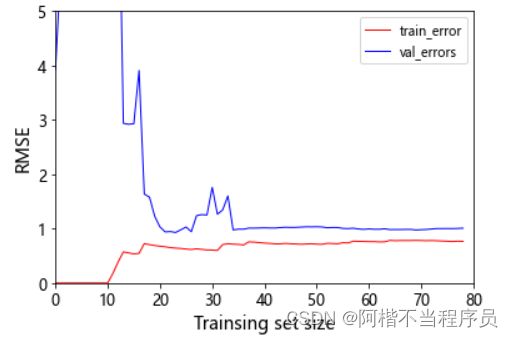
polt_learning_curves(polynomial_reg,X,y)
plt.axis([0,80,0,5])
plt.show()

degree值越大时，过拟合的风险也就越大。

正则化

用于解决过拟合问题。

对权重参数进行惩罚，让权重参数尽可能平滑一些。

• 岭回归

岭回归是线性回归的正则化版本，即在原来的线性回归的 cost function 中添加正则项，以达到在拟合数据的同时，使模型权重尽可能小的目的。

# 岭回归
from sklearn.linear_model import Ridge
np.random.seed(42) # 设置种子
# 数据准备
m = 20
X = 3*np.random.rand(m,1)
y = 0.5 * X + np.random.randn(m,1)/1.5 + 1

# 测试集
X_new = np.linspace(0,3,100).reshape(100,1)

def plot_model(model_class,polynomial,alphas,**model_kargs): # **：接收多个参数存入字典model_kargs
    for alpha,style in zip(alphas,('b-','g-','r-')): # 正则化项，转为元组类型：[(a1,'b-'),(a2,'g-')...]
        # 实例化模型
        model = model_class(alpha,**model_kargs)
        if polynomial:
            model = Pipeline([('poly_features',PolynomialFeatures(degree=10,include_bias=False)),
              ('StandardScaler',StandardScaler()),
              ('lin_reg',model)])
        model.fit(X,y)
        y_new_regul = model.predict(X_new) # 预测值
        lw = 2 if alpha > 0 else 1
        plt.plot(X_new,y_new_regul,style,linewidth = lw,label= 'alpha={}'.format(alpha))
    plt.plot(X,y,'b.',linewidth = 3)
    plt.legend()

plt.figure(figsize=(10,5))
plt.subplot(121)
plot_model(Ridge,polynomial=False,alphas = (0,10,100))
plt.subplot(122)
plot_model(Ridge,polynomial=True,alphas = (0,10**-5,1))
plt.show()

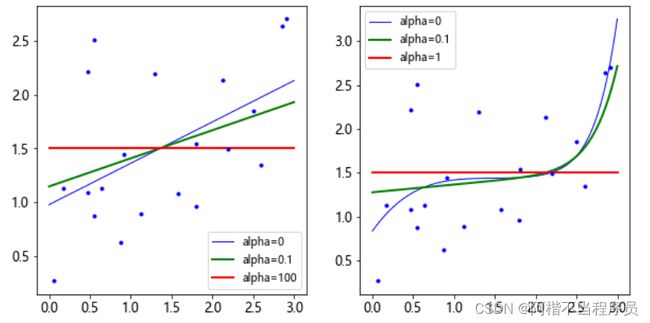
alpha = 0时，即无正则化项，曲线不稳定；

alpha = 1e-05时，曲线较平稳；

alpha = 1时，曲线更平稳，拟合效果最好。

alpha值越大时，惩罚力度越大，得到的决策方程越平稳。

• Lasso

就是加了一个绝对值项。

# Lasso
from sklearn import linear_model

plt.figure(figsize=(10,5))
plt.subplot(121)
plot_model(linear_model.Lasso,polynomial=False,alphas = (0,0.1,100))
plt.subplot(122)
plot_model(linear_model.Lasso,polynomial=True,alphas = (0,10**-1,1))
plt.show()