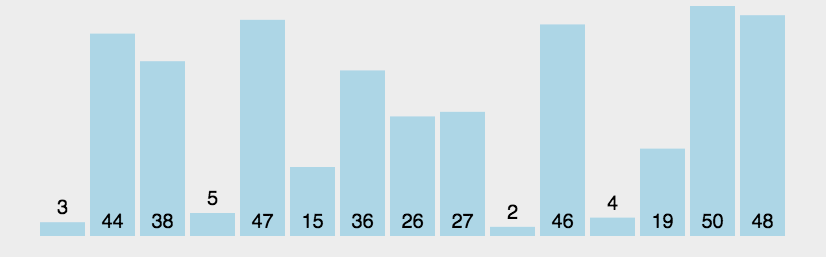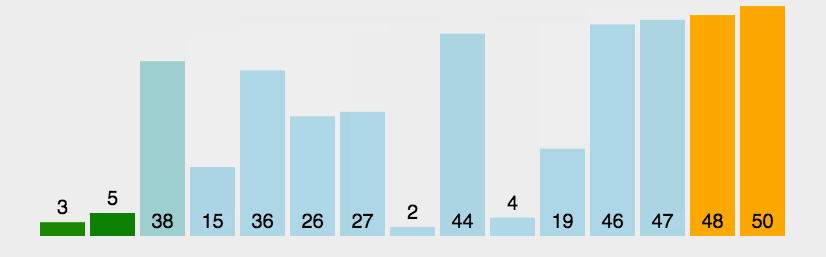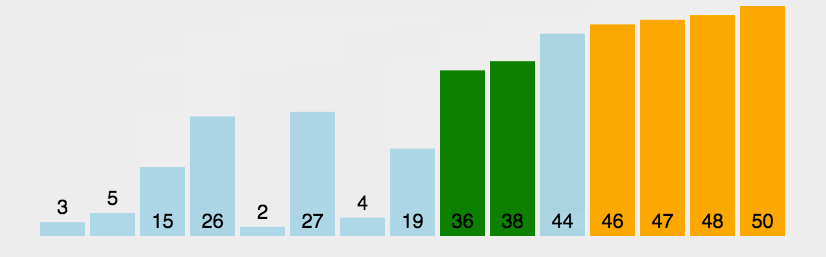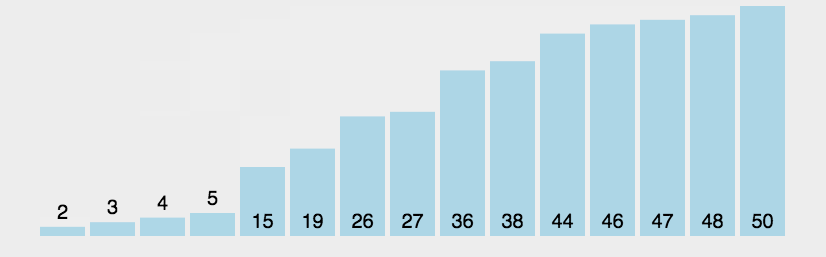数据结构 | 十大排序超硬核八万字详解【附动图演示、算法复杂度性能分析】
写在前面
2023年的第一篇博客,在这里先祝大家兔年快乐.
文章比较长,App端会比较卡,尽量到网页端访问
本文从学习到搜寻各种资料,整理成博客的形式展现足足花了一个月的时间,慢工出细活,希望本篇文章可以真正带你学懂排序,不再为写排序算法而苦恼
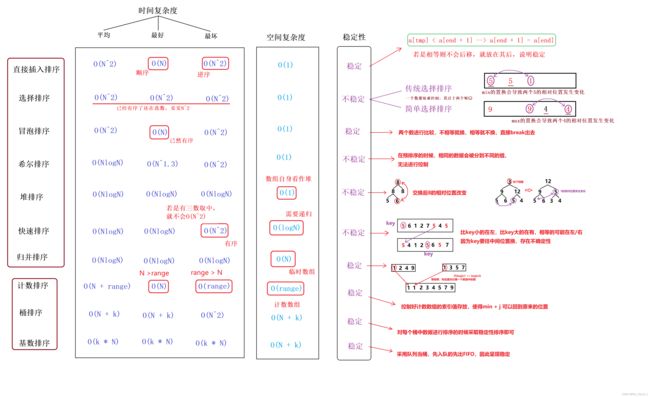
十大经典排序算法庖丁解牛细致剖析
- 一、直接插入排序【还阔以】
-
- 1、动图演示
- 2、算法思路简析
- 3、代码分析与详解
- 4、复杂度分析
- 二、希尔排序【一匹黑马】
-
- 1、动图演示
- 2、算法思路简析
- 3、排序过程总览
- 4、代码分析详解
- 5、复杂度分析
- 三、选择排序【不太行】
-
- 1、动图演示
- 2、代码解析
-
- 2.1 传统选择排序
- 2.2 简单选择排序【优化后】
- 3、复杂度分析
- 四、堆排序【⭐重点掌握⭐】
-
- 1、动图演示
- 2、堆的概念及结构
- 3、向下调整算法【核心所在】
-
- 3.1 算法图解分析【高处不胜寒趁早做打算】
- 3.2 代码考究精析
- 4、升序建大堆 or 小堆❓
- 5、如何进一步实现排序❓
- 6、复杂度分析
- 五、冒泡排序【有点夭折】
-
- 1、动图演示
- 2、思路简析
- 3、算法图解分析单趟排序过程
- 4、代码详解 + 性能优化
- 5、复杂度分析
- 中转站——插入、选择、冒泡三者的性能比较【✔】
-
- 1、分化性能对比分析
- 2、冒泡排序的特定优势 —— 序列已经有序
- 3、插入排序的特定优势 —— 序列接近有序
- 六、快速排序【⭐⭐⭐重点掌握⭐⭐⭐】
-
- 1、Hoare版本【左右指针法】
-
- 1.1 动图演示
- 1.2 算法基本思路明细
- 1.3 整体递归排序图预览
- 1.4 思考:为何相遇位置一定会比key要来得小❓
- 1.5 代码的详解与分析
- ⌚快速排序复杂度分析
-
- 快排缺陷1——待排序列呈现有序状态
- 快排缺陷2——递归层数过深导致栈溢出
- 快速排序优化
-
- 【三数取中法】—— 高性能优化
-
- 代码&算法图逻辑分析
- 性能测试
- 【左右小区间法】—— 小型优化
- 2、挖坑法
-
- 2.1 动图演示
- 2.2 基本思路简析
- 2.3 算法分解图
- 2.4 代码展示与详解
- 3、前后指针法
-
- 3.1 动图演示
- 3.2 基本思路简析
- 3.3 算法分解图
- 3.4 代码展示与详解
- 4、三路划分法
-
- 4.1 快速排序缺陷3——key值大量重复
- 4.2 算法思路简析
- 4.3 代码详解与过程分解
- 快速排序方法的“非递归写法”【校招要求✍】
-
- 递归的缺陷分析
- 非递归代码实现
- 七、归并排序【⭐重点掌握⭐】
-
- 1、动图演示
- 2、算法思路简析
- 3、递归实现
-
- 3.1 思路分析
- 3.2 代码详解
- 3.3 算法图解展示 && DeBug视频讲解【】
- 4、非递归实现【校招要求✍】
-
- 4.1 思路分析
- 4.2 普通情况展示【可恶的随机数】
-
- 代码详解
- DeBug详细断位分析
- 4.3 越界的特殊情况考虑
-
- 4.3.1 方法一【不修边界——部分拷贝】
- 4.3.2 方法二【修边界——整体拷贝】
- 4.4 小结
- 八、计数排序【还是不错的】
-
- 1、动图演示
- 2、算法思路简析
- 3、具体代码分析
- 4、复杂度分析
- 九、桶排序【局限性大】
-
- 1、动图演示
- 2、算法思路简析
- 3、代码详解与分析
- 4、DeBug调试分析
- 5、复杂度分析
- 十、基数排序【不常用】
-
- 1、动图演示
- 2、算法思路分析
- 3、代码分析与算法图解
- 4、复杂度分析
- 拓展:文件外排序【了解一下】
-
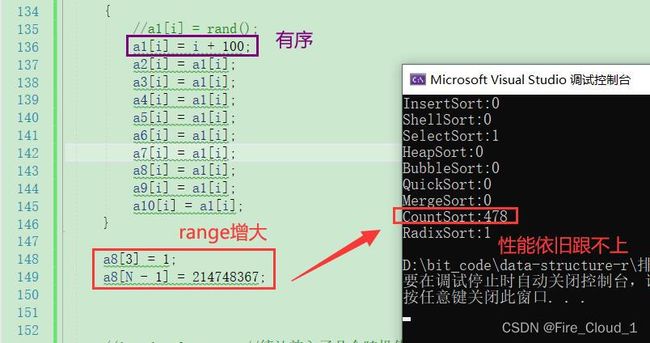
- 1、前言
- 2、思路解析
- 3、代码详解
- 整体代码展示
- LeetCode实战演练
- ⌚稳定性分析 + 各大排序算法性能测试
- ✒总结与提炼
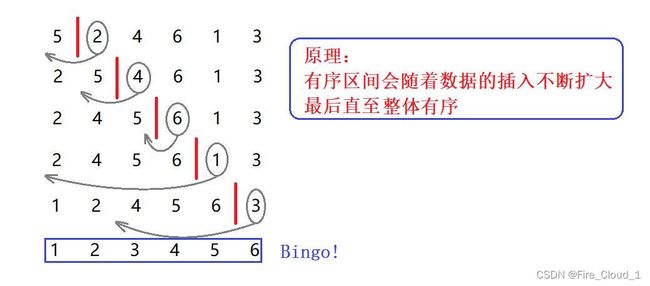
一、直接插入排序【还阔以】
1、动图演示
2、算法思路简析
【核心思路】:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列
- 实际中我们玩扑克牌时,就用了使用到了插入排序的思想。设想你发到一张牌为7,现在想将其放入你刚才已经整理好了牌堆中,这个牌堆就是有序序列,这张牌就是待插入的数据。通过生活中的场景来看,是不是更加形象一点呢
3、代码分析与详解
对直接插入排序有了一个基本的了解以后,我们需要将这个思想去转化为代码
很多同学一开始刚有点思路就开始写代码,甚至什么都不想直接开始写,然后运行报错一大堆,各种数组访问越界、边界问题没有考虑、代码逻辑混乱。这其实是写程序的一个大忌,我们应该逐步分析,从简单到复杂、从单趟的排序到整体的排序去过渡
①写出单趟的的插入过程
- 首先对于单趟的逻辑,因为是要将一个数插入到一个有序区间中去,不妨设这个区间的最后一个位置为【end】,那这个待插入数据的位置就是【end + 1】,我们要将这个待插入的数据保存起来,因为在比较的过程中可能会造成数据的后移,那这个数就会被覆盖了
- 接着将待插入的数据与有序区间的最后一个数进行比较,因为默认选择排升序,所以是要将小的数据放到前面,所以若是这个待插入数据比a[end]要小,那a[end]便进行一个后移,但是呢,随着数据的不断增大,有序区也会越来越大,此时待插入数据就不只是和有序区的最后一个数据做比较了,需要和前面的所有数进行一个比较,那么我们就要将这段逻辑放在一个循环里。这个循环什么时候结束呢?就是当这个【end < 0】为止
- 若是在中途比较的过程中发现有比待插入数据还要小或者相等的数,就停止比较,跳出这个循环,因为随着有序区间中数的后移,end后一定会空出一个位置,此时呢执行
a[end + 1] = tmp;就可以将这个待插入数据完整地放入有序区中并且使这个有序区依旧保持有序
int end;
int tmp = a[end + 1]; //将end后的位置先行保存起来
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end]; //比待插值来得大的均往后移动
end--; //end前移
}
else
{
break; //若是发现有相同的或者小于带插值的元素,则停下,跳出循环
}
}
a[end + 1] = tmp; //将end + 1的位置放入保存的tmp值
②利用循环控制每一趟插入排序
- 这一块我们只需要将单趟的插入过程放在一个循环中即可,逐渐扩大这个有序区,因此【end】即为每次递增的变量i。
- 这里要注意的一点是循环的结束条件
i < n - 1,这里不可以写成i < n,若是写成这样那么【i】最后落的位置就是【n - 1】此时end获取到这个位置后取保存tmp的值时就会造成造成数组的越界访问,那么这个位置就会出现一个随机值,所以大家在写这种循环的边界条件时一定提前做好分析,在运行之前保证心里胸有成竹
for (int i = 0; i < n - 1; ++i)
{
int end = i;
//单趟插入逻辑...
}
整体代码展示
/*直接插入排序*/
void InsertSort(int* a, int n)
{
//不可以< n,否则最后的位置落在n-1,tmp访问end[n]会造成越界
for (int i = 0; i < n - 1; ++i)
{
int end = i;
int tmp = a[end + 1]; //将end后的位置先行保存起来
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end]; //比待插值来得大的均往后移动
end--; //end前移
}
else
{
break; //若是发现有相同的或者小于带插值的元素,则停下,跳出循环
}
}
a[end + 1] = tmp; //将end + 1的位置放入保存的tmp值
}
}
运行结果
![]()
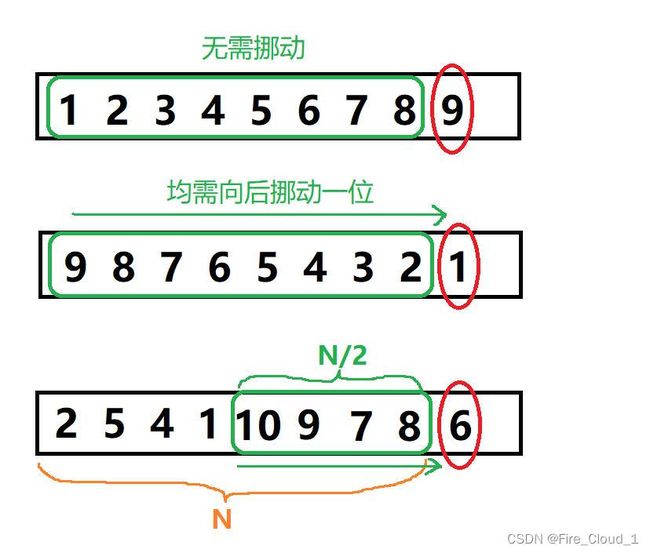
4、复杂度分析
【时间复杂度】:O(N2)
【空间复杂度】:O(1)
- 看了代码之后我们再来看看其复杂度,首先是对于时间复杂度,这块看的是这个排序算法执行的次数,那对于直接插入排序这一块来说,取决于数据数据的分步,设想若是一些随机的数字,然后每次取到的tmp值可能就需要插入到中间、前面、最后三种情况
- 【最好的】是每一趟的内部比较都不需要移动数据,只需要遍历一下这个数组即可,那时间复杂度就是O(N);
- 【中间的】就是数据需要后移一般,那时间复杂度就是O(N/2)即O(N);
- 【最坏的】是需要插入到最前面的情况,因为对于tmp前面的每一个数字都需要向后挪动一位,也就意味着tmp要和这个数组的所有数字进行一个比较,然后又有N个数需要进入,此时时间复杂度就是O(N2);
- 对于空间复杂度计算的额外的空间,在这里我们只是定义了一些变量,并没有去申额外的空间,因此空间复杂度为O(1)
二、希尔排序【一匹黑马】
1、动图演示
2、算法思路简析
基本思想:希尔排序又称缩小增量排序。是按照每次的gap值,也就是增量,对原本的数据进行一个分组,对每组使用直接插入排序算法排序。增量【gap】随着排序次数的增加而减少
当增量减少到1时,整个序列恰好被分为一组,算法便终止。
【核心思路】:通过预排序将大的数尽快放到后面,将小的数尽快放到前面
- 对于希尔排序,上面说过,其隶属于插入排序,是对直接插入排序的优化。
- 对于gap增量,当gap > 1时,都是对原先的数组进行的一个预排序,也就是将其接近有序;而当gap最终等于1时,则是已经接近有序,这时再用一次直接插入排序即可
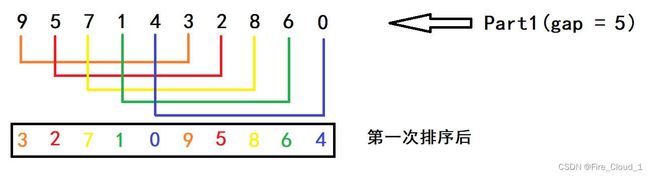
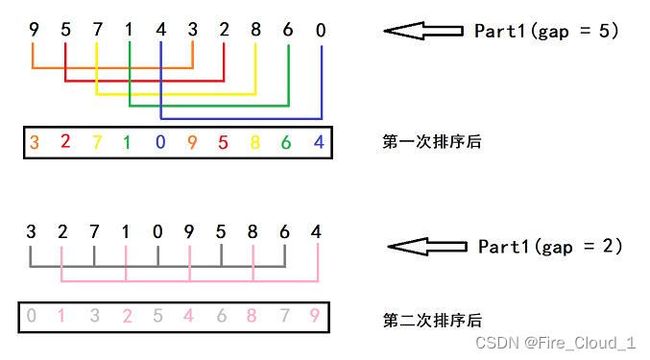
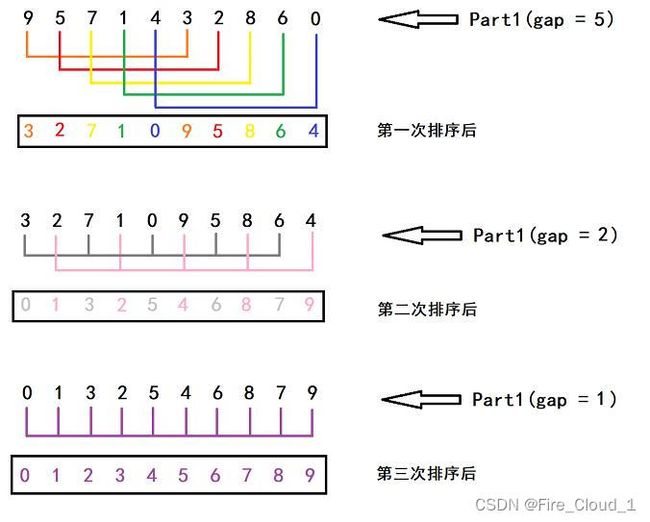
3、排序过程总览
- 我们看到这里有10个数,因此gap = 10 / 2 = 5,也就是每个数字之间间隔为5,然后以将它们分为很多组,若是后者比前者大,则进行一个交换
- 上面是第二次排序后地结果,此时得gap = 5 / 2 = 2,所以增量为2的是一组
- 以上,便是第三次排序后的结果,可以看到,第三次得gap = 2 / 2 = 1,因为间隔为1,也就是全体数据为一组,那就是最后进行一次直接插入排序即可
4、代码分析详解
还是一样,我们由简至易,做单步分析
①确定单趟排序的过程
- 对于希尔排序,上面说到过,它是隶属于插入排序,所以对于单趟的逻辑只需要在直接插入排序的基础上做一个修改即可,但是对于移动的间距我们肯定需要去做一个控制,因为希尔排序的数是被分成了一组一组的,而且每一组的数之间的间隔取决于gap的大小,因此 对于
tmp = a[end + gap];,保存的就是当前待比较元素的后移gap位元素 - 在实现后移的过程中也是移动gap步,对于end也是同理
- 那在跳出循环之后的tmp也是要放在
a[end + gap]的地方
int gap = 3;
int end;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
②循环控制每一趟插入排序
- 对于这个有两种解法,都给大家点到
Way1:
for (int i = 0; i < n - gap; i += gap) //一组一组走
Way2:
for (int i = 0; i < n - gap; i++) //一位一位走
我们来看看上面两种情况的不同之处
- 对于
i += gap来说,在排序的过程中是先把每一组先排好,再排下一组 - 对于
i++来说,在排序的过程中第一组排好了一个数据后,i++又进行下一组的排序,每次只插入一个,然后到后面又回到这一组来,像是一个轮回的过程。你可以自己去试试看
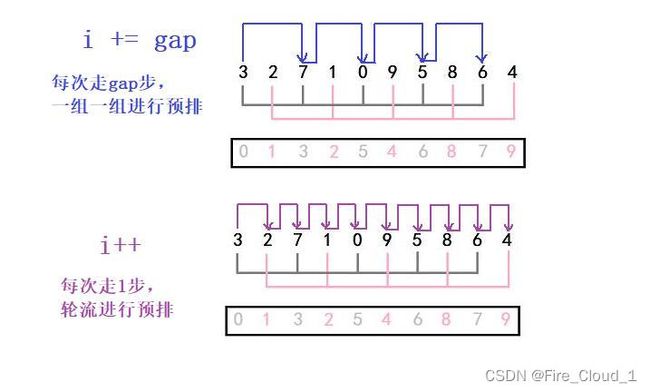
③单趟gap的排序控制好后,我们就需要去控制这个增量gap了,网上很多写法都是gap /= 2,这种比较经典一些,也是我上面所展示的一种
int gap = n / 2;
for (int j = 0; j < gap; ++j)
{
gap /= 2;
for (int i = j; i < n - gap; i += gap)
{ //一组一组走
//单趟插入过程...
}
}
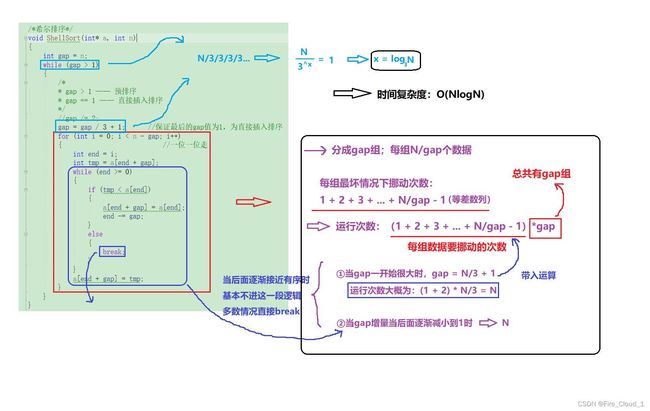
- 但是在这里,我会优先采用下面这种写法,因为当gap越大的时候,数字跳动得越快;当gap越小的时候,数字跳动的间距越小,此时会更进一步得接近有序,所以我们要将gap尽快地进行缩小,但是/3之后可能在最后无法使【gap = 1】,那此时的话就需要在最后加上一个1使得最后一次缩小gap增量的时候可以使其到达1
int gap = n;
while (gap > 1)
{
/*
* gap > 1 —— 预排序
* gap == 1 —— 直接插入排序
*/
//gap /= 2;
gap = gap / 3 + 1; //保证最后的gap值为1,为直接插入排序
for (int i = 0; i < n - gap; i++)
{
//单趟插入过程...
}
}
整体代码展示
/*希尔排序*/
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
/*
* gap > 1 —— 预排序
* gap == 1 —— 直接插入排序
*/
//gap /= 2;
gap = gap / 3 + 1; //保证最后的gap值为1,为直接插入排序
for (int i = 0; i < n - gap; i++)
{ //一位一位走
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
运行结果
- 然后我们通过单层gap结束后进行打印再来观察一下希尔排序的数据变化
5、复杂度分析
【时间复杂度】:O(NlogN)
【空间复杂度】:O(1)
- 根据上面的代码,分析了一下希尔排序的时间复杂度
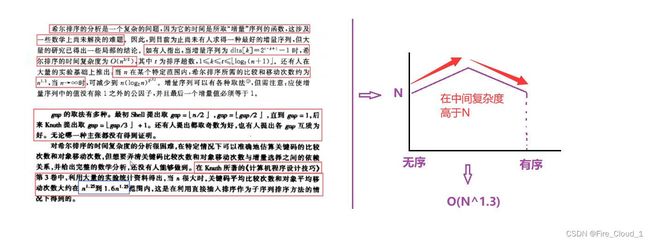
- 但这也仅仅似乎根据我们写的代码来看,实际上希尔排序的时间复杂度不是O(NlogN),而是O(N1.3),是不是感觉很奇怪,在在一些市面上较受欢迎的书上也写到这一块复杂度涉及到数学方面的逻辑推理,因此以我的数学能力可能也就能做到这些了╮(╯▽╰)╭
- 大家只能要能够计算出O(NlogN)就行了,如果有读者数学很好的当然也是可以做到,然后对于希尔排序时间复杂度最坏是O(N2),这一点上面也已经写出了,最坏情况就是等差数列的时候,例如5个数要挪动4下,3个数要挪动2下。。。N个数要挪动N - 1下
- 然后是有关希尔排序的空间复杂度,这一块还是和插入排序一样,只是在内部定义了一些变量,并没有去申请一些额外的空间,因此空间复杂度为O(1)
三、选择排序【不太行】
1、动图演示
2、代码解析
有关选择排序,大家应该是见过不少,这里我会讲两种,一种是传统的选择排序,一种则是我改进之后略微优化一些的选择排序
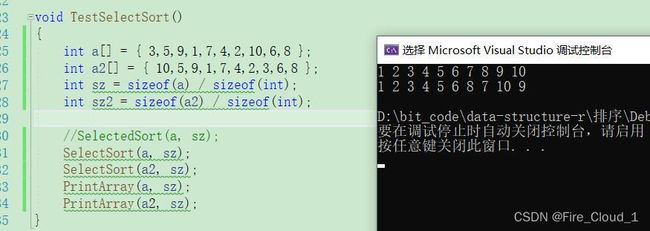
2.1 传统选择排序
- 首先来看看传统一些的选择排序,思路很简单,通过上面的动图可以看出,每次首先记录下i的位置,然后将这个位置保存起来,内部循环是在遍历从【i + 1】到【n - 1】这个区间中是否有小于当前保存的i的值,若是有,则使用k再记录下这一个下标,
if (a[j] < a[k]) k = j;一直寻找,直到搜寻完这个区间为止 - 在搜寻完成后取比较,若是
a[k] != a[i]则表示需要交换k和i这两个位置的数据,将它们交换之后小的数就会跑到前面了 - 接着再进入下一轮的比较i++,重复上面的过程,不断地将小的数换到前面来,那整个序列也就会逐渐呈现有序了
整体代码展示
void SelectedSort(int* a, int n)
{
for (int i = 0; i < n - 1; ++i)
{
int k = i;
for (int j = i + 1; j < n; ++j)
{
if (a[j] < a[k]) k = j;
}
if (a[k] != a[i])
{
swap(&a[k], &a[i]);
}
}
}
- 理解了传统的选择排序后,再去学习其他的排序算法就会发现对于选择排序来说一看性能就不是很好,没错,它就是非常明显的O(N2),我们在最后一个模块在做具体分析
运行结果
2.2 简单选择排序【优化后】
- 好,重点来讲一讲优化后的简单选择排序,需要设置的遍历可能有点多,看下图即可
- 设头为begin,尾为end,再设置一个最小值和一个最大值,然后在
[begin,end]这段区间里去不断寻找然后更新最大值和最小值 - 在每一次遍历完后将最小值换到begin的位置,最大值换到end的位置,接着
begin++;end--;不断缩小需要查找的区间。这样小的数就会被慢慢放到前面,大的数就会被慢慢放到后面,序列便会逐渐趋向有序
- 首先来看一下代码:思路有了,代码并不是难事
/*简单选择排序*/
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int mini = begin;
int maxi = begin;
for (int i = begin + 1; i <= end; ++i)
{
if (a[i] < a[mini])
mini = i;
if (a[i] > a[maxi])
maxi = i;
}
swap(&a[begin], &a[mini]);
swap(&a[end], &a[maxi]);
begin++;
end--;
}
}
- 再来看看运行结果
- 可以看到,我这个给出了两组测试案例,但是从结果来看似乎第二组测试案例并没有成功排好序,这个时候我们应该对代码的敏感,若是有一组测试案例跑不过那么这个代码就是有问题的
- 但是从思路来看确实是感觉没什么问题?其实这就是最大的问题,当你觉得自己的代码没有问题的时候,其实在某些极端场合下就会出问题,所以在写代码的时候要考虑得周全一些
- 接下去通过DeBug调试来看看究竟除了什么问题
- 看完下面这三张图,相信你应该了解到问题处在哪里了,因为在一开始这个最大值和begin是重合的,因此在将最小值交换到begin位置的时候这个maxi位置所在的最大值就会被交换到另一个地方,此时就出问题了
- 所以在交换完mini和begin位置之后,要判断一下maxi是否在begin的位置,若是则将maxi做一个更新即可
if (maxi == begin) //若是最大值和begin重合了,则重置一下交换后的最大值
maxi = mini;
整体代码展示
/*简单选择排序*/
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int mini = begin;
int maxi = begin;
for (int i = begin + 1; i <= end; ++i)
{
if (a[i] < a[mini])
mini = i;
if (a[i] > a[maxi])
maxi = i;
}
swap(&a[begin], &a[mini]);
if (maxi == begin) //若是最大值和begin重合了,则重置一下交换后的最大值
maxi = mini;
swap(&a[end], &a[maxi]);
begin++;
end--;
}
}
运行结果
3、复杂度分析
【时间复杂度】:O(N2)
【空间复杂度】:O(1)
- 对于选择排序这一块来说,其实是很明显的O(N2),无论是对于传统的选择排序还是简单选择排序都是这样
- 我们优化过后的选择排序还是每次减少两个数,因为是每次遍历是选出最大值和最小值放到两个端点处,所以遍历的数字个数是N + (N - 2) + (N - 4) + (N - 6)… + 2,将它们加起来差不多就是O(N2)
- 但是对于传统的选择排序来说,就是妥妥的O(N2)了,首先记录下第一个位置的数据,然后从【i + 1】开始做遍历,遍历(N - 1)个数字遍历完后若是找到一个比起小的数则进行交换,然后第二次又从第二个数开始,遍历(N -2)个数,以此往复,每次遍历的数一个一个的减少,依旧呈现的是一个等差数列,所以便为O(N2)
- 空间复杂度这一块也是一样,为O(1)
四、堆排序【⭐重点掌握⭐】
1、动图演示
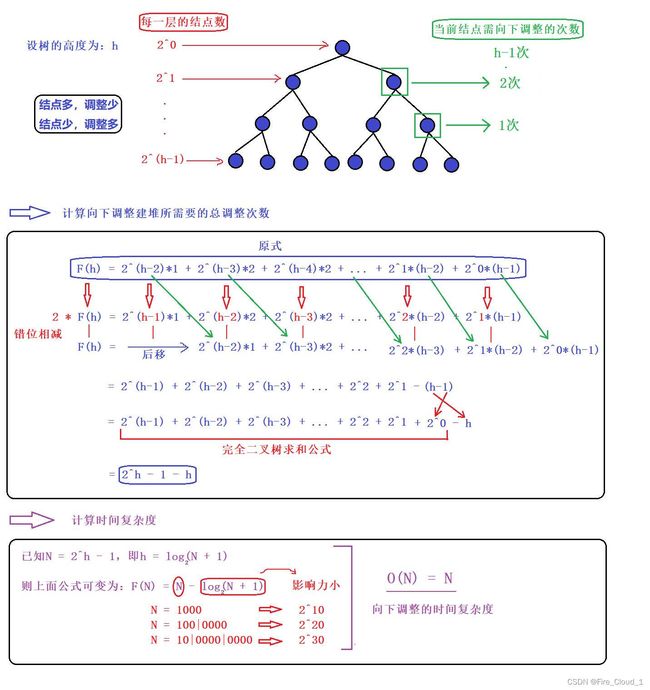
2、堆的概念及结构
首先在学习堆排序前要了解堆是个什么东西
如果有一个关键码的集合K = { k0, k1, k2,…,kn-1 },把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中。并满足:Ki <= K2*i+1 且 Ki <= K2*i+2 ( Ki >= K2*i+1 且 Ki >= K2*i+2 ) i = 0,1,2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆
堆的性质
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树
- 从上图可以看出,对于【堆】而言,其实就是一种完全二叉树,但是呢,它又在完全二叉树的基础上再进一步形成一个区分,也就是分为【大根堆】和【小根堆】
- 可对于这种树形的结构,其实并不是它在内存中真正的样子,这只是我们为了更好地理解而想象出来的;它在内存中真正的样子应该是右边那样,也就是像一种数组的存储方式,对于这种逻辑结构和物理结构的区分,我在一文带你彻底搞懂单链表也有做过详细区分。那既然是数组,一定可以使用【下标】来访问其中的元素。
- 这其实就可以得出一种结论,就是这个堆中的各个结点直接它是存在一种关系的,我们在树和二叉树的基本概念讲到了父亲结点和孩子结点。那此时我们是否可以用下标来表示一下父亲结点和孩子结点直接的关系呢,就像下面这样
【lchild = parent * 2 + 1】 左孩子
【rchild = parent * 2 + 2】 右孩子
parent = (lchild - 1)/ 2 或者 parent = (rchild - 2)/ 2 ===> 【parent = (child - 1) / 2】
- 如果觉得难以理解,可以将下面的下标带入进入演算一下,就可以发现确实是这样

- 为了再进一步加深对堆的一个理解,我们来实际地看一下有关堆这一块的题目
- 可以看出,对于【堆】而言,要么是大堆,要么是小堆,不一定是呈现升序或者是降序,这涉及到的是我们后面的堆排序,但是对于父亲和孩子的关系来说,一定是父亲【<=或者>=】它的孩子,而且对于任何一个子树而言都必须成立,这才能对称做一个【堆】
3、向下调整算法【核心所在】
对于堆排序来说,核心的一块就是【向下调整算法】,领悟了这一块,那你堆排序也就掌握一半了
3.1 算法图解分析【高处不胜寒趁早做打算】
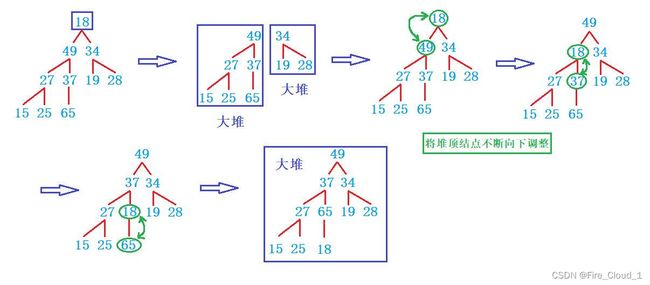
- 对于向下调整算法,最主要的一个前提就是根节点的左右子树都要是大堆或者都要是小堆,就根结点不满足,才可以去进行一个向下调整
- 此时就需要使用到这个【向下调整算法】,当然我这个是大堆的调整,小堆的话刚好相反。原理:找出当前结点的两个孩子结点中教大的那一个换上来,将这个【18】换下去,但是呢此时还不构成大堆,因此我们还需要再去进行一个调整,一样是上面的找法,然后直到这个【18】的孩子结点到达【n - 1】就不作交换了,因为【n - 1】就相当于是位于数组下标的最后一个值
3.2 代码考究精析
清楚了向下调整算法的主要原理和思路,接下去我们就要将其转化为代码
- 首先对于向下调整算法来说我们需要传入的不是孩子,而是父亲,因为调整的是堆顶数据,也就是根节点,而对于根节点来说是没有父亲的,所以就是父亲,然后的话需要的是这个堆的大小【n】,因为这个我们在循环体的结束条件时需要用到
void Adjust_Down(int* a, int n, int parent)
- 上面是知道孩子求父亲,这里的话就是知道父亲求孩子了,但是有同学说,孩子不是有两个吗,为什么我只写了一个【child】,这里的话你也可以写成【lchild】和【rchild】,但是呢这在下面进行比较的时候代码会显得比较冗余,你可以先写写试试看,再和我这个做对比
- 因为我们是需要和孩子结点中大的那个做交换,因为我这里是直接假设左孩子比较大
int child = parent * 2 + 1;
- 接下去呢将左右孩子的值进行一个比较,若是右孩子来的大就将child++,也就顺其自然变成了右孩子。可以看到这个if判断里还加了一个【child + 1 < n】,这个的话其实就是进行一个右孩子的越界访问判断,因为我们是在进行一个不断向下调整的过程,因此肯定会到达倒数第二层,此时它的左孩子可能是存在的,但若是它的右孩子不存在了,那么在后面去访问这个【child + 1】就会变成越界访问,是一个非法操作
//判断是否存在右孩子,防止越界访问
if (child + 1 < n && a[child + 1] > a[child])
{
++child; //若右孩子来的大,则转化为右孩子
}
- 然后是循环内部的逻辑,和【向上调整算法】一样,就是一个比较和迭代更新的过程
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
下面是整段代码
/*向下调整算法*/
void Adjust_Down(int* a, int n, int parent)
{
int child = parent * 2 + 1; //默认左孩子来得大
while (child < n)
{ //判断是否存在右孩子,防止越界访问
if (child + 1 < n && a[child + 1] > a[child])
{
++child; //若右孩子来的大,则转化为右孩子
}
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
4、升序建大堆 or 小堆❓
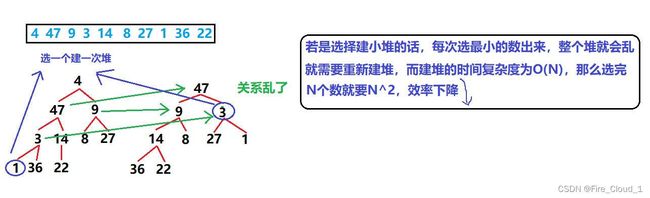
- 我们知道,对于升序就是数组前面的元素小,后面的元素大,这个堆也是基于数组建立的,那就是要堆顶小,堆顶大,很明显就是建【小堆】
- 一波分析猛如虎,我们通过画图来分析是否可以建【小堆】
- 可以看到,对于建小堆来说,原本的左孩子结点就会变成新的根结点,而右孩子结点就会变成新的左孩子结点,整个堆会乱,而且效率并不是很高,因此我们应该反一下,去建大堆
//建立大根堆(倒数第一个非叶子结点)
for (int i = ((n - 1) - 1) / 2 ; i >= 0; --i)
{
Adjust_Down(a, n, i);
}
5、如何进一步实现排序❓
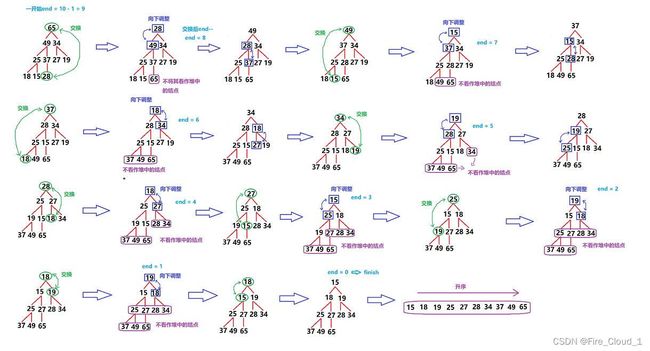
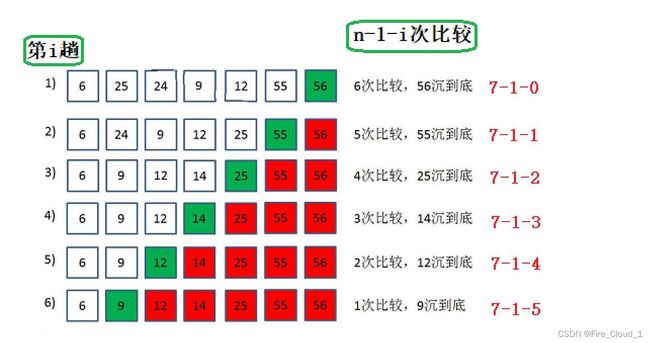
- 有了一个大堆之后,如何去进一步实现升序呢,此时我们堆排序的思路首先就是将堆顶数据与堆底末梢数据做一个交换,然后对这个堆顶数据进行一个向下调整,将大的数往上调
- 可能有同学很疑惑为什么要将大的数往上调呢?因为我们每次都需要将堆顶的数据交换下去,并且不将其看做堆中的组成部分,这样每次将最大的一一撤离堆中,就可以从后往前逐渐形成一个升序的序列,最后调整完后就是一个小堆,将其转化为数组的形式就是最后的结果了
具体过程如下
- 对照代码,好好分析一下堆排的全过程吧
/*堆排序*/
void HeapSort(int* a, int n)
{
//建立大根堆(倒数第一个非叶子结点)
for (int i = ((n - 1) - 1) / 2 ; i >= 0; --i)
{
Adjust_Down(a, n, i);
}
int end = n - 1;
while (end > 0)
{
swap(&a[0], &a[end]); //首先交换堆顶结点和堆底末梢结点
Adjust_Down(a, end, 0); //一一向前调整
end--;
}
}
整体代码展示
/*交换*/
void swap(int* x, int* y)
{
int t = *x;
*x = *y;
*y = t;
}
/*向下调整算法*/
void Adjust_Down(int* a, int n, int parent)
{
int child = parent * 2 + 1; //默认左孩子来得大
while (child < n)
{ //判断是否存在右孩子,防止越界访问
if (child + 1 < n && a[child + 1] > a[child])
{
++child; //若右孩子来的大,则转化为右孩子
}
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
/*堆排序*/
void HeapSort(int* a, int n)
{
//建立大根堆(倒数第一个非叶子结点)
for (int i = ((n - 1) - 1) / 2; i >= 0; --i)
{
Adjust_Down(a, n, i);
}
int end = n - 1;
while (end > 0)
{
swap(&a[0], &a[end]); //首先交换堆顶结点和堆底末梢结点
Adjust_Down(a, end, 0); //一一向前调整
end--;
}
}
运行结果
6、复杂度分析
【时间复杂度】:O(NlogN)
【空间复杂度】:O(1)
- 堆排序这一块的时间复杂度比较难算,因为在一开始我们要使用向下调整算法去建立一个大堆,所以首先我们来分析一下【建堆】这一块的时间复杂度
- 建堆这一块是O(N),接下去还要对每一个结点自下而上去进行调整
- 对于调整这一块的话就是每次交换堆顶和堆顶的数据,首先将交换下来的这个数据不当做堆中的结点,也就是将其当做有序区间的一部分,因为我们建立的是大堆,所以每次交换下来的堆顶数据一定是最大的,接着,将每一个交换到堆顶的数再去进行一个向下调整,因此可以看出每一个数字的调整的这一块的复杂度就是 (log2N) ,数组中有N个数需要调整做排序,因而就是O(Nlog2N)。
- 最后将建堆和调整有序做一个合并就是O(N + Nlog2N),取影响结果大的那一个就是O(Nlog2N),这也就是堆排序最终的时间复杂度
- 对于空间复杂度而言还是O(1),那有同学就说这个堆不是由数组构建而来的,那就需要传进来一个数组了。这一块应该对照其他排序算法,对于【int* a】只是外界传进来的一个数组罢了,并不算是我们又重新申请空间,是这个函数本身就具有的,而对于空间复杂度而言我们计算的是【额外消耗的空间】
五、冒泡排序【有点夭折】
1、动图演示
2、思路简析
核心思想 :根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置。即每次两两比较,将大(小)的往后方,像一个冒泡的过程
交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
3、算法图解分析单趟排序过程
- 下面是冒泡排序的单趟比较过程
4、代码详解 + 性能优化
看了上面的单趟冒泡过程,相信你对冒泡排序有了一个基本的认识,每次进行两两比较,将大的数往后放,这个过程就像是冒泡一样,接下去我们来看看代码该如何书写
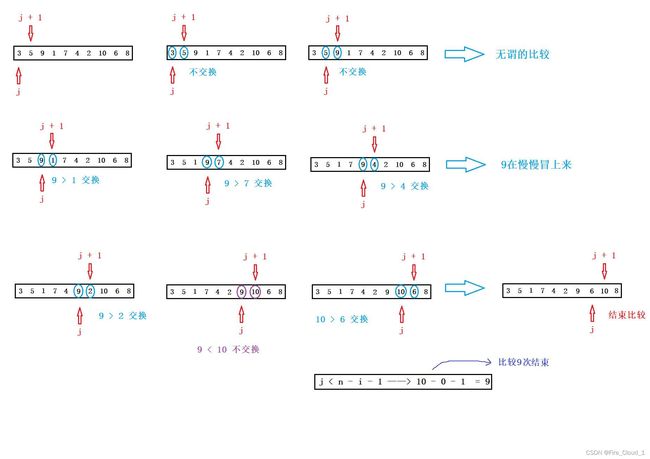
①单趟的冒泡过程
- 首先要写出内部的单趟过程,但是对于冒泡排序来说,内部比较的次数是根据外部循环遍历的次序来的,所以先给出模板
- 先不要看结束条件,就看内部逻辑,可以看出就是一个比较然后交换的过程
for (int j = 0; j < n - i - 1; ++j)
{
if (a[j] > a[j + 1])
swap(&a[j], &a[j + 1]);
}
②外部的循环遍历
- 这个外部的起始条件不一定写成我这样,你也可以写成
for (int i = 1; i < n; ++i),那么你内部的单趟冒泡结束条件就要变一下了,否则的话就会造成数组访问越界的问题
for (int i = 0; i < n - 1; ++i)
{
//单趟冒泡...
}
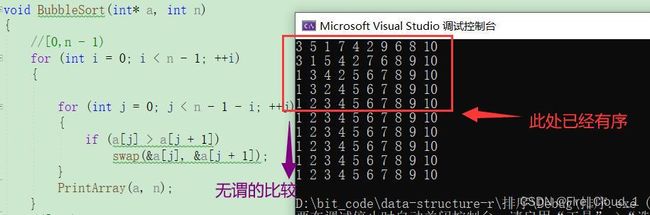
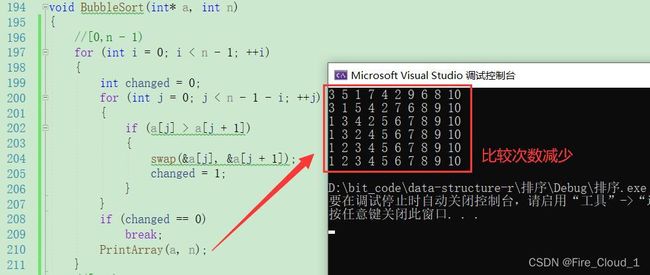
- 下面是整个冒泡排序的过程演示。因为有挺多同学对于冒泡排序的边界条件还不是很清楚,所以这里也讲得细致一些。希望在讲解这么多之后,有不懂冒泡排序的小伙伴可以彻底搞懂
- 其实对于冒泡排序来说,是可以再继续优化的,因为每一趟冒泡的两两比较中,出现前一个数小于后一个,也就是我在上面画过的单趟的冒泡过程,此时是不需要进行交换的,但是计算机还是进行了一个比较。这些其实是一个无谓的比较,因此我们可以对冒泡排序再做一个性能上的优化
- 具体的优化过程就是设置一个【标记值】,当每一趟冒泡的比较的过程发生了交换,则使用标记值对其进行一个记录;若是没有进行交换了,则表示已经有序了,就退出本轮的比较
- 首先我们来追踪打印一下究竟浪费了多少次比较过程
- 接下去我们对其进行一个优化
整体代码展示
/*冒泡排序*/
void BubbleSort(int* a, int n)
{
//[0,n - 1)
for (int i = 0; i < n - 1; ++i)
{
int changed = 0;
for (int j = 0; j < n - 1 - i; ++j)
{
if (a[j] > a[j + 1])
{
swap(&a[j], &a[j + 1]);
changed = 1;
}
}
if (changed == 0)
break;
PrintArray(a, n);
}
//[1,n)
//for (int i = 1; i < n; ++i)
//{
// for (int j = 0; j < n - i; ++j)
// {
// if (a[j] > a[j + 1])
// swap(&a[j], &a[j + 1]);
// }
//}
}
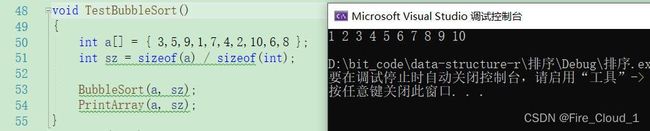
运行结果
5、复杂度分析
【时间复杂度】:O(N2)
【空间复杂度】:O(1)
- 对于冒泡排序而言,我们通过上面的讲解了解了其运行过程,就是每一个数与其后的n - i个数进行比较,若是符合条件则进行交换,不算我们优化之后的,算法运行的次数就是N + (N - 1) + (N - 2) + (N - 3) + … + 2 + 1,结合起来运算就是一个等差数列,那么其时间复杂度显而易见就是O(N2)
- 对其进行优化之后虽说没有O(N2),但也只是减少了一些比较次数。冒泡排序最好的情况就是O(N),也就是当序列已经呈现有序的状态下,此时在排序的过程中只需要遍历一下这个数组即可,因为完全不需要交换
- 空间复杂度也是一样的O(1)
中转站——插入、选择、冒泡三者的性能比较【✔】
这一块是后来加的,刚好在看完这三个排序算法后进行一个对比,也可以起到巩固的效果
- 我们通过表格的对比来看看这三个排序的平均、最好和最坏的时间复杂度
| 排序算法 | 平均情况 | 最好情况 | 最坏情况 |
|---|---|---|---|
| 直接插入排序 | O(N2) | O(N) | O(N2) |
| 简单选择排序 | O(N2) | O(N2) | O(N2) |
| 冒泡排序 | O(N2) | O(N) | O(N2) |
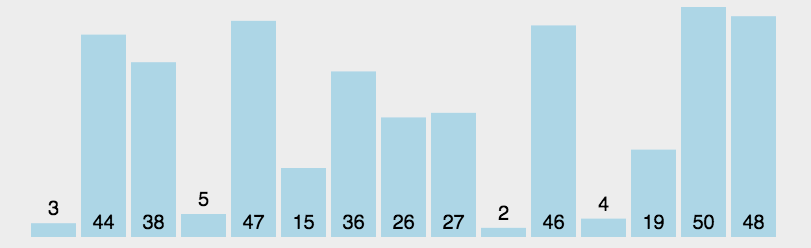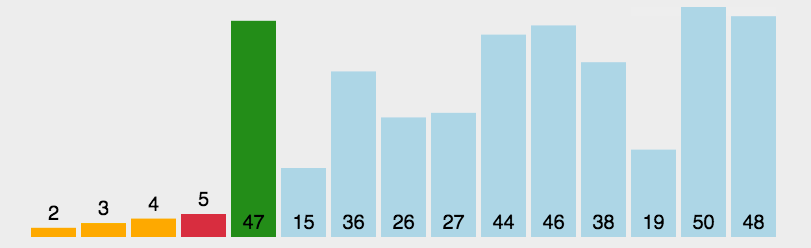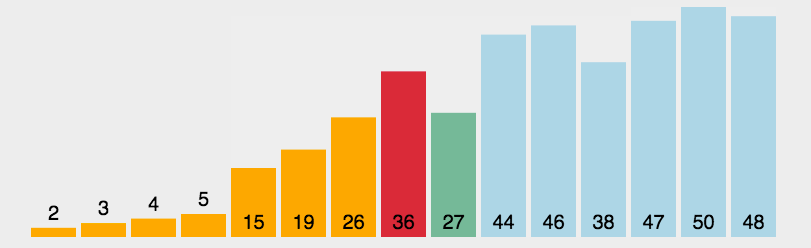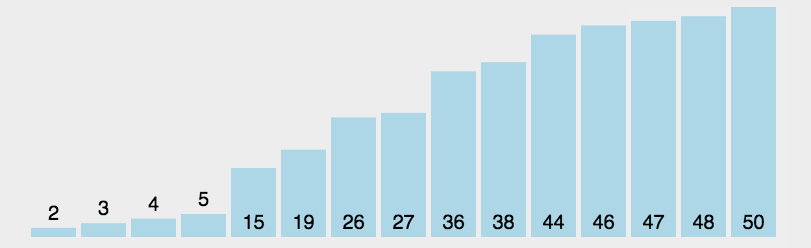
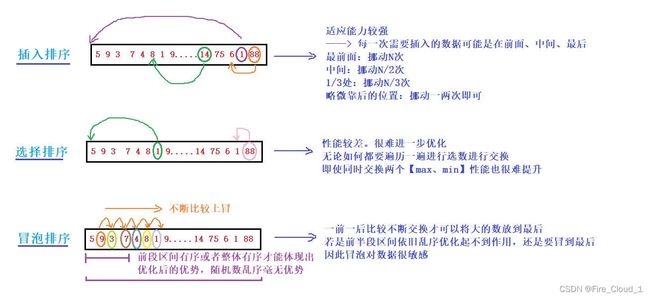
- 可以看到,三者的平均情况都是O(N2),而且对于【选择排序】来说,无论何种情况,和我们上面说的一样,均需要遍历一遍然后进行两两交换,是妥妥的O(N2)
- 但是对于【直接插入排序】和【冒泡排序】在最好的情况下却可以达到O(N),为什么可以到达O(N)呢?是因为在一些特殊的场合下他们的性能可以达到最优
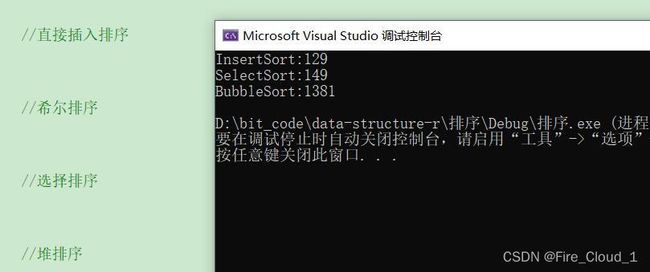
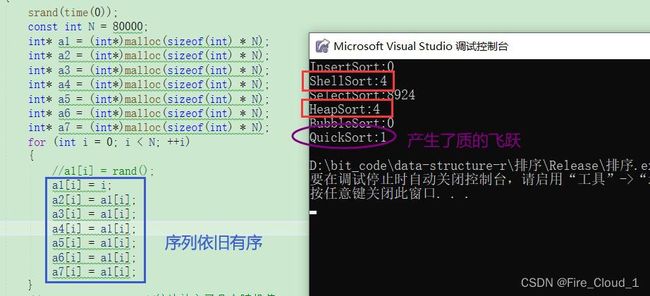
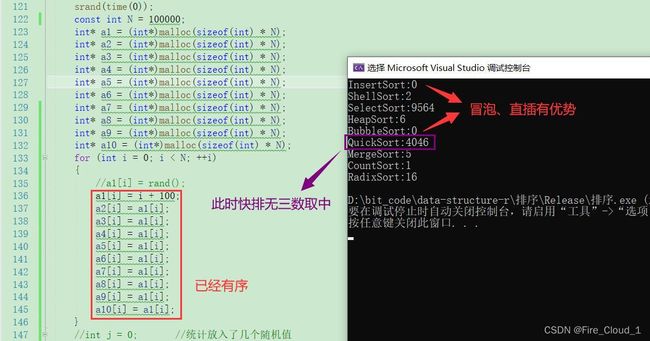
- 首先通过算法性能比较测试一下它们对于固定的数据进行排序所需要耗费的时间,这个是毫秒【代码在文末】
- 从直观上可以看出,插入排序来得最优,其次是选择排序,接下去是冒泡排序,而且对于冒泡排序来说性能差的不是一点半点,还是在我们做了优化之后的,那可以设想优化之前还要更加慢一些
- 但是这其实不能看出它们谁更优,因为我产生的是一些随机数,因此一些数据的分步会导致排序算法的性能受到波动
1、分化性能对比分析
我们通过对比来看看它们之间究竟差在哪里
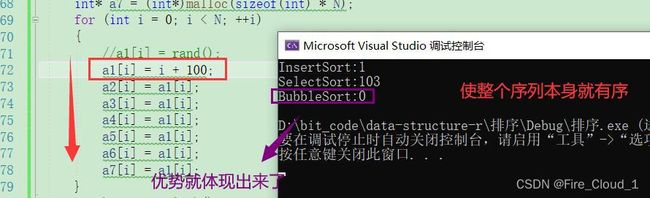
2、冒泡排序的特定优势 —— 序列已经有序
- 这样看来就可以知晓为何冒泡排序会比性能最差的选择排序还要来的慢。那冒泡要在何种场景下才能展现出其优势呢?
- 可以看到这里我将整个序列故意弄成有序,此时冒泡排序的优势就出来了,因为已经有序的话就不需要再去进行比较,直接break出了这一趟的冒泡,所以性能就会大幅上升,但是它也就在这种情况下才能体现出优势,在乱序且数据量大的情况下毫无优势
- 而且可以看出,在序列有序的情况下,直接插入排序的效率也很高
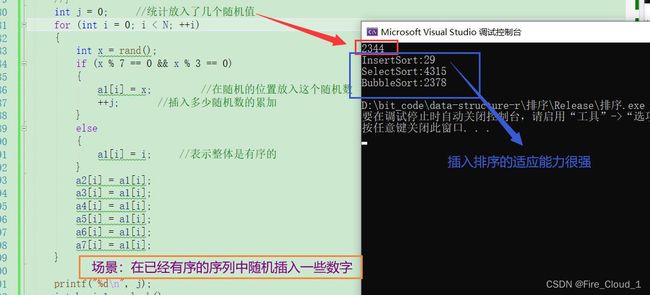
3、插入排序的特定优势 —— 序列接近有序
- 有一个同学问了一个问题说:若是整个序列接近有序,那么冒泡和选择是不是都有优势呢?
- 这其实是不对的,刚才说了,对于冒泡排序需要【整体都有序】或者【前半区间有序】那么才能真正体现出优化后的优势,对于整体接近有序的序列,我们考虑去使用【直接插入排序】
- 看到上图,我在特定的场景下做了测试,可以看出对于插入排序来说这种场景很好地展现出了它的优势
- 仔细观看上面两幅图可以看出对于选择排序来说,无论在何种场景下都显得不是很优,因此我们在选择排序算法的时候尽量不要选择这种排序。而且对于这三种排序算法的使用,要非常清楚适合他们的场景,这样才可以将其性能优势发挥到最大
六、快速排序【⭐⭐⭐重点掌握⭐⭐⭐】
1、Hoare版本【左右指针法】
1.1 动图演示
1.2 算法基本思路明细
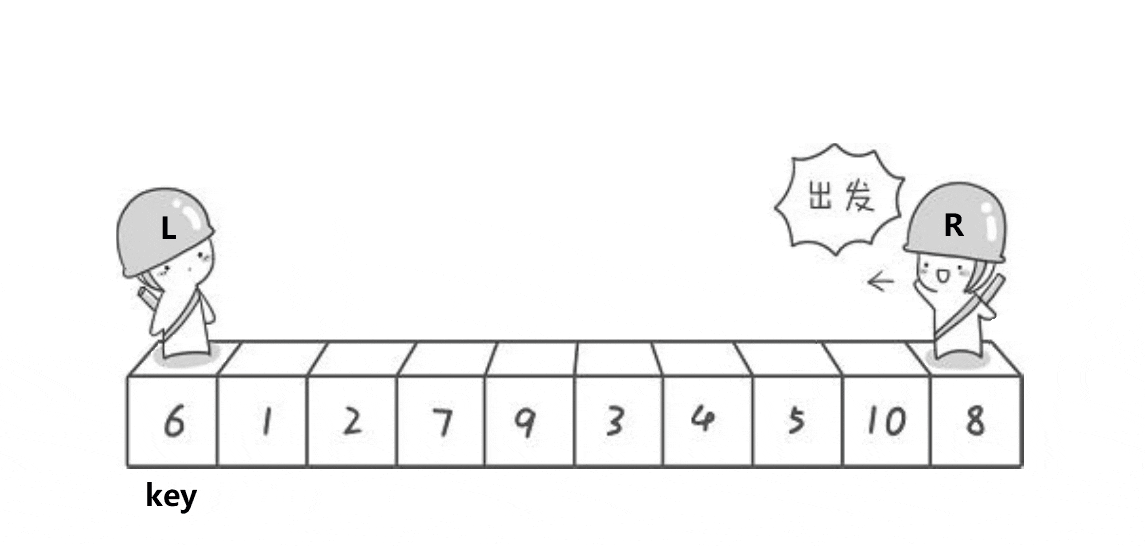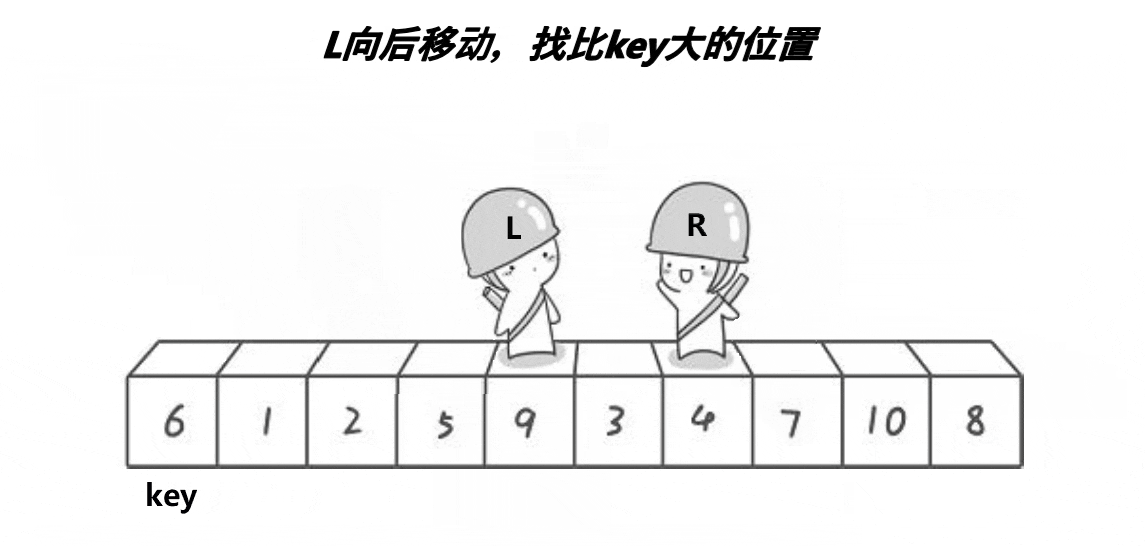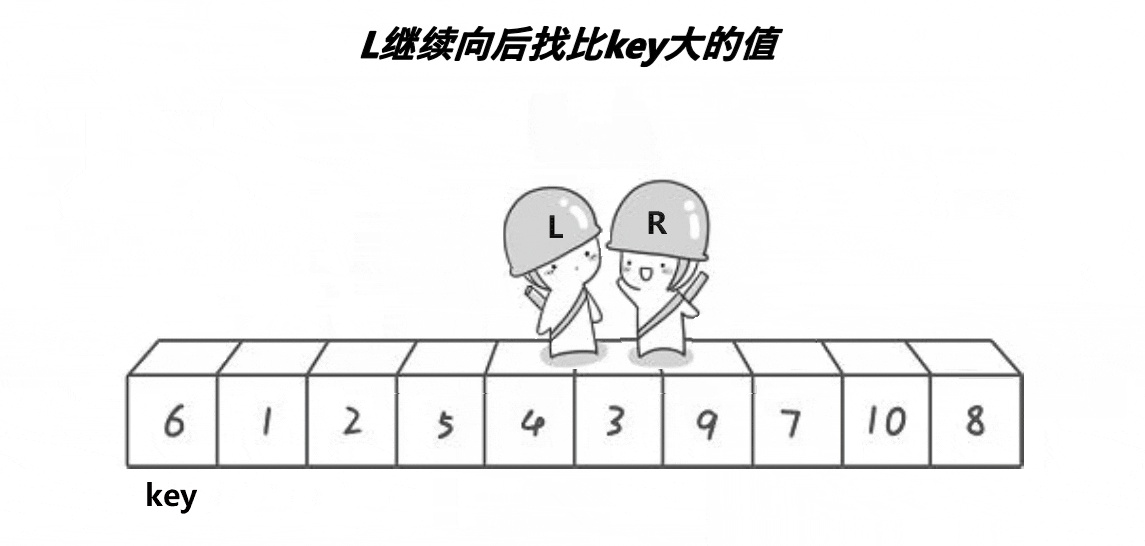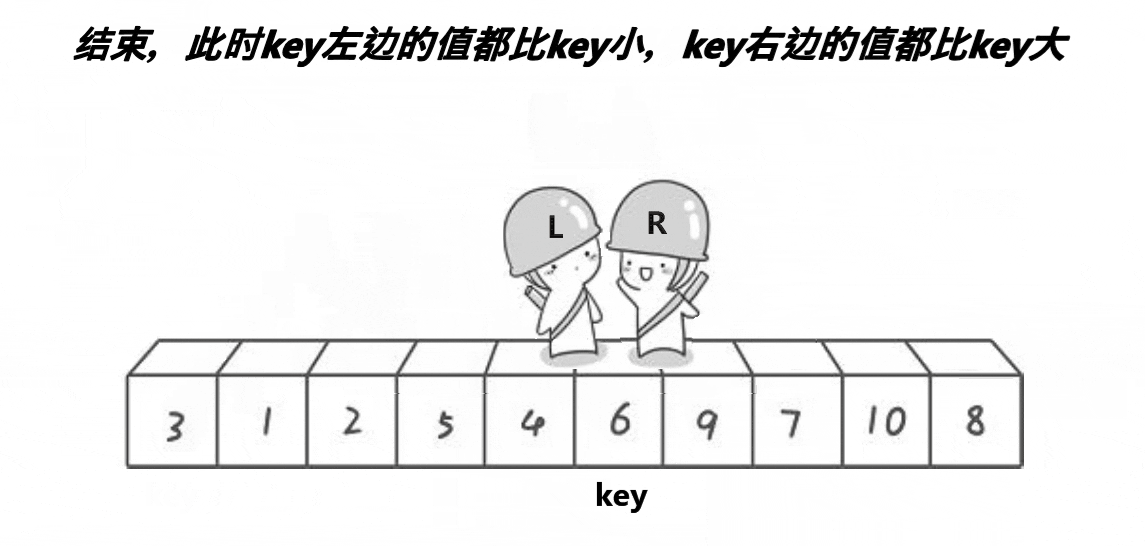
首先来说一说对于hoare版本的这个排序思路的概要,也就是大家常说的左右指针法
- 这个版本为什么叫hoare呢?因为快速排序就是由是Hoare于1962年提出的一种二叉树结构的交换排序方法
【核心思路】:任取待排序元素序列中的某元素作为基准值(一般我们选择取最左边),按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程(递归),直到所有元素都排列在相应位置上为止
1.3 整体递归排序图预览
- 了解了核心思路之后呢,来看看我为你精心绘制的一幅排序简要图
- 可以看到当第一次找到这个左右指针相遇后的位置时,基准值就被交换到了中间,接着呢继续对左右区间进行重复的操作,首先直至左区间有序后,会进行回调;此时再去递归右区间,当右区间也有序之后,那整体也就有序了
- 可以看到这是不是和我们在链式二叉树中说到的【先序遍历】有异曲同工之秒呢
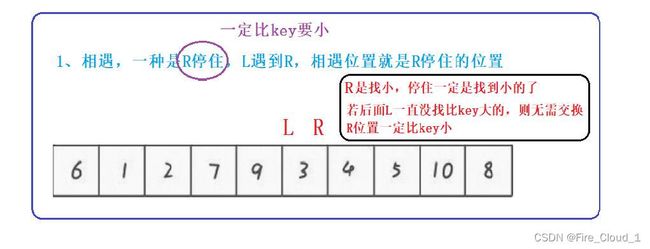
1.4 思考:为何相遇位置一定会比key要来得小❓
首先再度明确规则:找最前的值,也就是left作为基准值,然后让right去找比基准值小的数字。即左边做key,右边先走
①第一种【R停住】:右边R找到小的了,停住了。此时左边L在找的过程中并没有找到比key大的,因此二者只能会面,那么会面的这个值一定要比key要来的小,因此交换后不会出问题
②第二种【L停住】:R在右边找到了比key小的,L在左边找到了比key大的,二者进行交换,此时L上的数就是比key要小的(交换过来了)。后面R在进行第二轮搜寻的时候并没有再找到比key小的了,只能和L相遇然后和key交换,此时也不会出问题
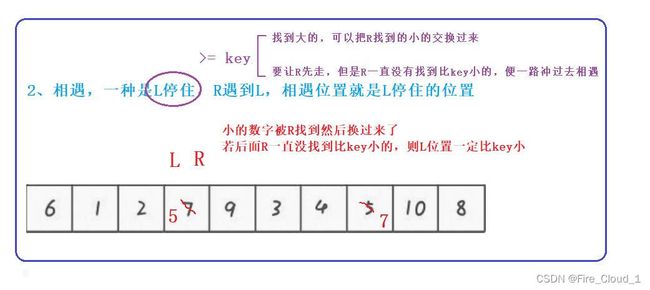
③第三种【L停住】:这是一种特殊情况,因为是R先走,但是呢R在一开始就没有找到比key来得小的值,因此它会在一个循环当中一直跑一直跑,直到和L相遇为止,那有的同学说L为什么不跑?因为L要等到R找到对应的值之后它才能跑
1.5 代码的详解与分析
先给出整体代码,你可以先看看,然后再听我分析
- 这里的代码将单趟的循环进行了一个抽取,为的是后面写多种方法时修改代码方便
/*快速排序 —— hoare版本(左右指针法)*/
int PartSort1(int* a, int begin, int end)
{
/*
* 找小 —— 是找真的比我小的
* 找大 —— 是找真的比我大的
* --->相等均要略过
*
* 还要防止越界【left < right】
*/
int left = begin;
int right = end;
int keyi = begin; //以最左边作为对照值记录,右边先走
while (left < right)
{
//右边找比keyi所在位置小的值,若是 >= 则忽略(加上=防止死循环)
while (left < right && a[right] >= a[keyi])
{ //left < right —— 防止特殊情况越界
right--;
}
//左边找比keyi所在位置大的值,若是 <= 则忽略
while (left < right && a[left] <= a[keyi])
{
left++;
}
//都找到了,则交换
swap(&a[left], &a[right]);
}
//最后当left和right相遇的时候将相遇位置的值与keyi位置的值交换
swap(&a[left], &a[keyi]);
keyi = left; //因keyi位置的值被交换到相遇点,因此更新准备分化递归
return keyi;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return; //最后递归下去区间不存在了,进行递归回调
int key = PartSort1(a, begin, end); //单趟排序获取key值
//左右区间分化递归
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}
- 其他的都不会有很大问题,我们主要来讲讲内部的循环逻辑
- 看到内部的这两段循环就是来控制L与R进行寻找走动的代码,也是快速排序的核心♥所在
//右边找比keyi所在位置小的值,若是 >= 则忽略(加上=防止死循环)
while (left < right && a[right] >= a[keyi])
{ //left < right —— 防止特殊情况越界
right--;
}
//左边找比keyi所在位置大的值,若是 <= 则忽略
while (left < right && a[left] <= a[keyi])
{
left++;
}
- 但是有的同学在一上来可能就会写成这样,也是很多同学的通病(没有考虑到特殊情况)
//右边找比keyi所在位置小的值,若是 >= 则忽略(加上=防止死循环)
while (a[right] > a[keyi])
{ //left < right —— 防止特殊情况越界
right--;
}
//左边找比keyi所在位置大的值,若是 <= 则忽略
while (a[left] < a[keyi])
{
left++;
}
- 原因就是以下两点
⚠没控制端点导致越界风险
⚠没考虑相等情况导致死循环
- 接下去要说的就是第一次交换结束后的分化递归
- 我要特别强调的就是这一句,也就是重置这个keyi,这个keyi不是新的keyi值,而是因为keyi被交换到了left所在位置,因此我们要做个标记方面后面的递归可以进行左右划分,当然你直接使用left或者right也是可以的,就是不要使用keyi就行了,否则这个区间就会异常
keyi = left; //因keyi位置的值被交换到相遇点,因此更新准备分化递归
- 两边的递归只需要修改一下左区间的右边界值和右区间的左边界值就可以了
//左右区间分化递归
QuickSort1(a, begin, keyi - 1);
QuickSort1(a, keyi + 1, end);
- 既然要递归,那么一定需要递归的结束条件,也就是这个
if (begin >= end)
return; //最后递归下去区间不存在了,进行递归回调
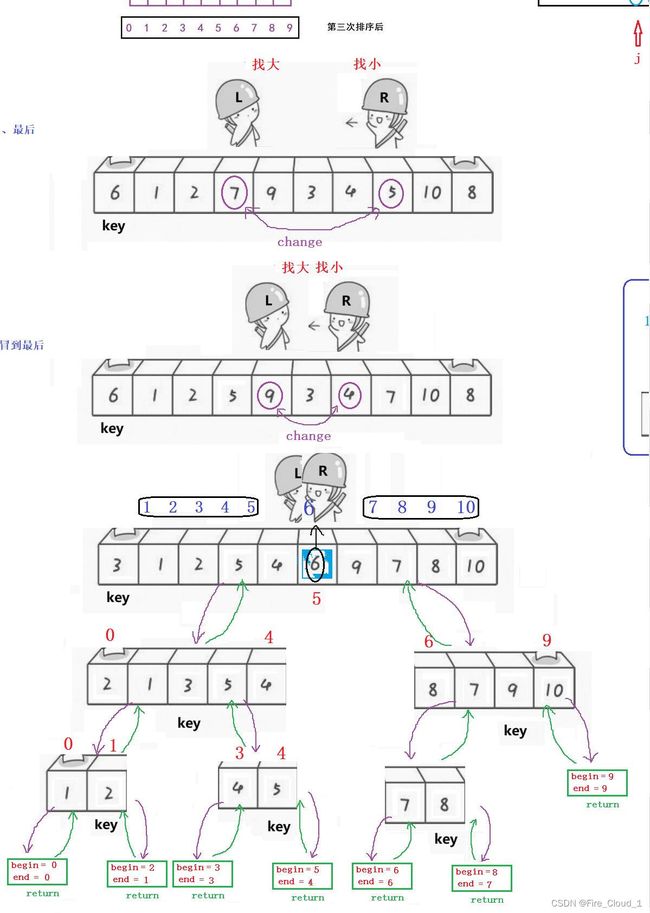
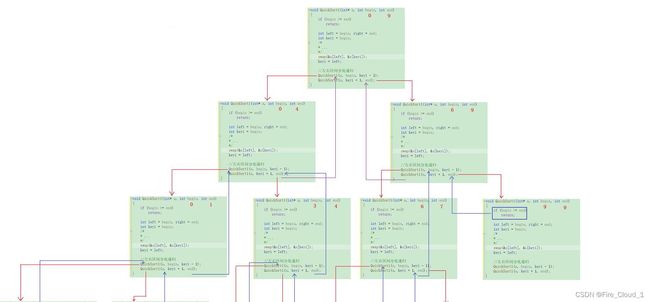
- 来画画递归展开图进一步了解快排的过程吧,尝试着自己动手试试✒️
⌚快速排序复杂度分析
【时间复杂度】:O(NlogN)
【空间复杂度】:O(logN)
看了Hoare版本的快排后,我们立马来分析一下其时间复杂度,因为后面要对其进行优化,所以要提前讲一下复杂度这一块
- 理解了快速排序的总体流程后,你应该了解了它是每次通过左右两个指针的遍历和key进行一个比较然后进行交换,因而将其列入【交换类排序】,但是呢在找出第一个key之后,就需要进行一个左右分化递归,最后直至左右区间均有序之后,整体才算有序。因此对于快排来说,也可以算作是一种分治类排序
- 通过这个思维我们来看看快排的时间复杂度该如何描述
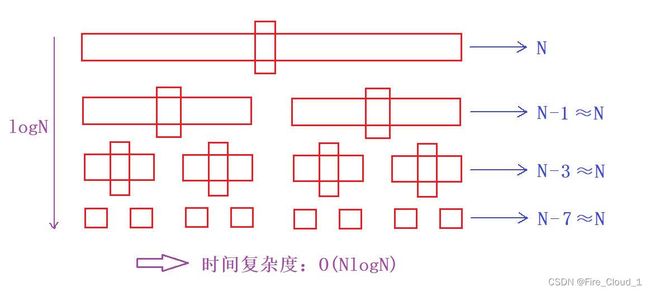
- 可以看到,横向是每一次要搜寻遍历的数字个数,随着key值不断地确定,在递归的过程中便慢慢减少,但这些在【大O渐进法】看来只是常数级的,因此可以忽略,那么每一次的遍历次数就是N
- 那需要遍历多少回呢,这就要看递归的深度了,假设我们每次找到的key值都在中间,那每一次的递归就都是一个二分,也可以看成是一个二叉树的样子,那根据【堆排序】来看很明显可以知晓这个次数是【logN】;
- 最后就可以得出快排的时间复杂度为O(NlogN)。
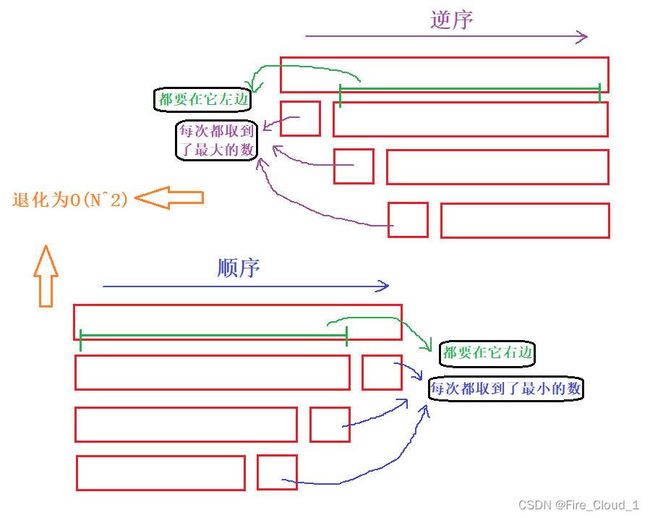
快排缺陷1——待排序列呈现有序状态
- 但是在学习了时、空复杂度之后知道对于时间复杂度有最好、最坏和平均只分,O(NlogN)只是快速排序的最好情况,从上图可以看出这是一棵满二叉树,但是呢,在一些场合下这个数据的分步是非常混乱而且不合理的,因此有些情况下很难达到O(NlogN)
- 为什么这么说呢,因为对于快排来说有一种致命的数据序列,那就是有序,无论是【顺序】还是【逆序】,它都招架不过来
- 假设你在左边选到了一个最大的数做key,此时这个序列还是逆序。但是呢要将比它小的数都放到它左边,此时不仅需要遍历N此,而且还要交换N此,妥妥的N2
- 假设你选取的key值是在最右边,选择了一个最小的数,此时这个序列还是顺序,那么就需要将它左边的所有数都放到这个key值的右边,也是N2
- 这么看来快速排序就退化成了O(N2)的排序算法,那有同学问:那快排还有什么用,都要退化了?因为快速排序很早就被发明出来了,被使用得很广泛,但是它也有一些自身的缺陷,所在在经过后人不断地修正过程中,也想出了一些对其进行优化的办法,例如像三数取中、小区间优化这些。还有人直接根据Hoare的这种思路,改进了快排,想出了类似于快排的思想,但是又有着不一样的地方的一些方法,就是我们下面要说到的两种:挖坑法、前后指针法
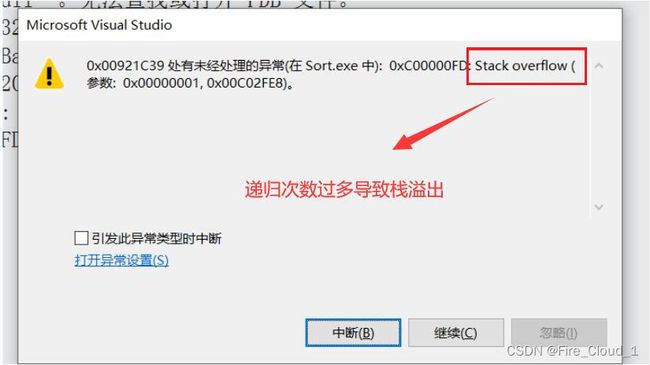
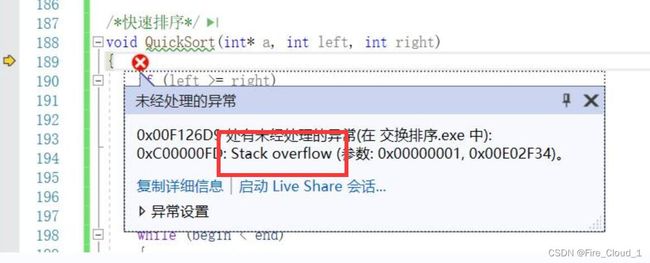
快排缺陷2——递归层数过深导致栈溢出
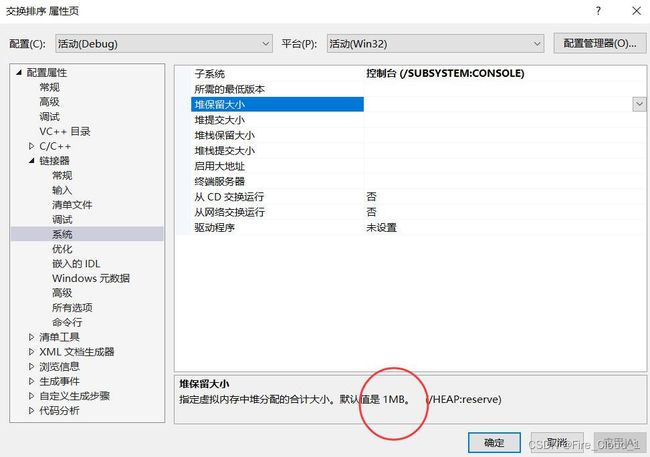
- 上面说到,快速排序除了对【有序序列】进行排序会退化之外,还有一点就是它需要进行层层递归,那既然是递归,就需要调用函数,那就需要建立栈帧,但是我们知道内存中的栈空间容量是有限的,在VS中默认大小只有1M,若是建立过多的栈帧,就会像下面这样产生栈溢出的风险
- 以上的这个栈溢出我是放在DeBug里面运行的,若是将运行版本修改为Release,那可能就不会出现这样的报错了,因为Release会对递归的调用次数进行一个优化,DeBug版本是专门用来调试用的,会有很多调试信息,因此内容多了,就会产生栈溢出
- 看到下面这张图,使我们刚才在分析时间复杂度的时候看到的,可以看到最后面这个二叉树是不断地在进行分叉,直至1为止然后才递归结束进行回调,但此时的递归深度可能已经很深了,已经是无法挽回了,那此时我们应该怎么办呢?不用怕,上面我们说到过了一种方法,就是专门针对这个的,也就是小区间优化法,在下一模块进行讲解
- 漏了一个空间复杂度忘说,对于快速排序和上面的五个排序不一样,它的空间复杂度不是O(1),而是O(logN)。那有同学对这个复杂度就没有一个概念了,我们一起来探讨一下
- 对于快速排序而言,不是在找出第一个keyi的位置之后就好了,还要其递归其左右区间,上面说到递归就要调用函数,函数就需要建立栈帧,低于栈帧来说,虽然不是什么很大的东西,但是其对比普通的变量而言还是会有一些消耗
- 所以在不断向下递归的过程中,就会产生许多栈帧,不过在回调的时候还是会去重复利用栈帧的,这么看来就像是一棵二叉树的样子,那就显而易见是未O(logN)了 ,但是当这个序列出现大量重复数据的时候,而且这个keyi还是重复数据,那么快速排序就会退化成像冒泡排序那样的O(N2),那么此时空间复杂度也会增加,呈现的便是一棵单边树的样子
快速排序优化
在分析完了快排的时间复杂度之后,也知晓了面对两种缺陷可以使用的优化方法,接下去我们来讲讲这两种方法
【三数取中法】—— 高性能优化
【针对待排序列呈现有序状态】
代码&算法图逻辑分析
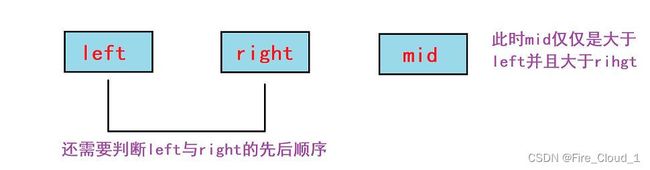
- 对于【三数取中法】,字面意思,就是从三个数中取出中间的那个数,我们设左边的数为left,设右边的数为right,然后它们的中间值为mid
- 我们通过算法图和代码一步步地来看一下
- 首先要先取出它的中间值,这里得【>>】是右移运算符,意思就是在二进制位上将其往右移动一位,对于二进制来说就是缩小两倍,也就是/2的意思
int mid = (left + right) >> 1;
- 然后我们给出第一层判断逻辑
int mid = (left + right) >> 1;
if (a[mid] > a[left])
{
if (a[mid] < a[right])
{ //left mid right
return mid;
}
//另外两种mid一定是最大的,比较left和right
else if (a[left] > a[right])
{ //right left mid
return left;
}
else
{ //left right mid
return right;
}
}
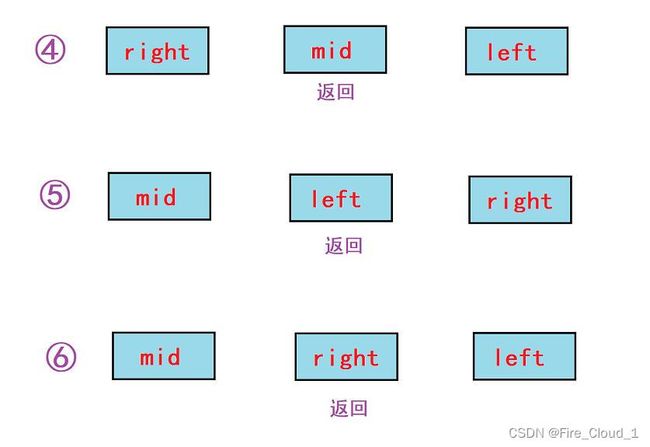
- 首先看到第一种,就是这个mid所在位置的值大于left所在位置的值的时候,继续进入判断,若是mid所在位置的值又小于right所在位置的值,那这个mid就处于中间位置了,直接返回即可
- 接着若是这个mid值不是小于right,那么它就一定处于最右侧,是最大的,这个时候我们内层的逻辑就是要去判断left和right的大小了
- 若是a[right] > a[left] ,那么right此时便在中间,返回right即可
- 若是a[left] > a[right] ,那么left此时便在中间,返回left即可
- 看完了第一层逻辑,我们再来看第二层逻辑
- 也就是当这个left所在位置的值要比mid所在位置的值要大的时候,也是有三种情况需要判断,若是mid所在位置大于right所在位置,则表示a[mid]为中间值,返回mid即可
- 若是mid所在位置的值小于等于right,那么a[mid]一定是最小的,此时同理,只需去比较a[left]和a[right]即可
else //a[left] >= a[mid]
{
if (a[mid] > a[right])
{ //right mid left
return mid;
}
//另外两种mid一定是最小的,比较left和right
else if (a[left] < a[right])
{ //mid left right
return left;
}
else
{ //mid right left
return right;
}
}
- 分析完之后一定要来看看这一块,涉及接口的调用
- 下面这两句直接写在单趟循环的逻辑中即可,若是在区间还存在的情况下,进到单趟分割进行比较可以直接选出一个中间值和最前面的begin值进行一个交换,
//三数取中
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]); //交换begin上的值和找出的中间值
- 此时begin位置的值就是最合适做key的,再去记录下这个key即可
int left = begin;
int right = end;
int keyi = begin; //以最左边作为对照值记录,右边先走
性能测试
- 上面了解了如何去优化快速排序,接下来我们来测试一下这个代码逻辑是不是真的可以实现性能优化
- 为什么说这个优化是高性能的优化,应该清楚了吧,有同学问为什么优化程度可以这么大呢?你带入一些特殊值放进O(N2)和O(NlogN)就知道为什么,完全不是一个级别的,所以对于序列有序这一点来说若是不加这个优化那对于快排是非常致命的
- 仔细观察上面两种图,是不是发现对于如此大的数据,但是【插入排序】和【冒泡排序】可以比其他O(NlogN)的排序还要快呢,这就是我们在上一模块中说到的
- 对于直接插入排序来说,序列接近有序性能达到最优
- 对于冒泡排序来说,序列有序性能达到最优
【左右小区间法】—— 小型优化
针对递归层数过深导致栈溢出
运用三数取中法,对快速排序进行了一个优化,接下去我们再来将一种优化方式,叫做左右小区间法
-
对于三数取中法,是在开头优化;对于左右小区间法,则是在结尾优化
-
好,这里给大家【简单】画了一张图,其实随着这个递归次数的增加,递归的层层深入,这个数据量也会被倍增,那么这个程序所需要消耗的内存就会越多,那我们有没有办法将最后的这几层递归消除呢?
- 这就要用到这个【左右小区间法】,什么叫左右小区间法呢?也就是随着这个区间被不断地划分,到了最后的那么几个区间,比如说每个区间只剩十个数的时候,我们就考虑将这个区间内的数再进行一个排序
- 那这个时候还是用快排吗,当然不是?如果用快排的话那和继续递归下去就没什么两样了,我们要使用其他的、用到此处最合适的排序算法
- 首先排除冒泡、选择,O(N2)的肯定不要
- 堆排序还要建堆,虽然性能可观,但只会增加繁琐度。
- 用希尔吗?不,这个地方不能用希尔,因为这个地方的数据量大概只有10个左右,并不多,希尔排序的话用在这里真的可以说是杀鸡用牛刀了,因为就这么十个数进不进行不排序完全没区别,因此也不合适
- 一个个排除下来,最后只剩下直接插入排序了,对,就是用它,虽然在有些场合下直接插入排序的性能不是很优,但是在此处只有10个数的情况,我们用直接插入排序最为合适
- 代码很简单,只需要判断一下当前递归进来的区间的数据个数是否 < 15,若是则直接来直接使用插入排序即可
- 这一块代码要写在总的快排代码中即可,而不是写在单趟中,因为是对不断递递归进来的区间个数进行的一个判断
//小区间优化
if ((end - begin + 1) < 15)
{
//在数据量少的时候改用直接插入排序
InsertSort(a + begin, end - begin + 1);
}
2、挖坑法
2.1 动图演示
2.2 基本思路简析
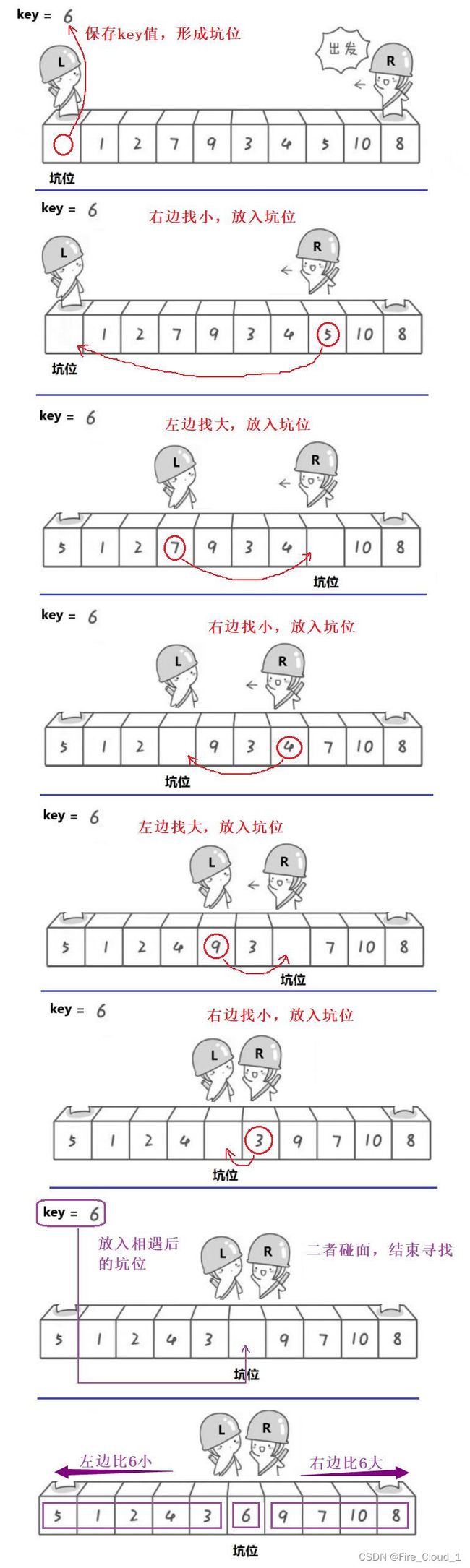
- 对于快速排序,还有第二种【挖坑法】,这种方法和左右指针法不同的地方在于它没有那么多缺陷,而且比较好理解
- 下面是它的排序步骤
①直接将最左端的值选出来作为key值,然后【右边找小】,放入坑位,然后更新坑位值为右侧找到的那个数所在的下标;
②出现了新的坑位后,【左边找大】,找到之后将数字放到新的坑位中,然后继续更新坑位。
③循环往复上面的步骤,直到两者相遇为止,更新相遇处为最新的坑位,然后将key值放入坑位即可,保证左边比key小,右边比key大
2.3 算法分解图
以下是动图的算法分解图,可以对照理解一下
2.4 代码展示与详解
- 首先展示一下代码
/*快速排序 —— 挖坑法*/
int PartSort2(int* a, int begin, int end)
{
//三数取中
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int left = begin, right = end;
int hole = left; //坑位
int key = a[hole]; //记录坑位上的值
while (left < right)
{
//右边找小,放入坑位,然后更新坑位
while (left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
//左边找大,放入坑位,然后更新坑位
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
- 我们来分析一下重点部分,也就是下面这块不断找小、找大并且填坑的逻辑
a[hole] = a[right]与a[hole] = a[left]就是在找到符合条件的数之后将其扔入坑中的过程hole = right与hole = left就是在填完上一个坑位之后更新坑位的过程
//右边找小,放入坑位,然后更新坑位
while (left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
//左边找大,放入坑位,然后更新坑位
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
- 最后的这一块
a[hole] = key就是在最后两者相遇后将原先记录的key值放入这个相遇的坑位。最后return hole这个坑位坐标即是找到的那个对照值所在的位置
3、前后指针法
3.1 动图演示
3.2 基本思路简析
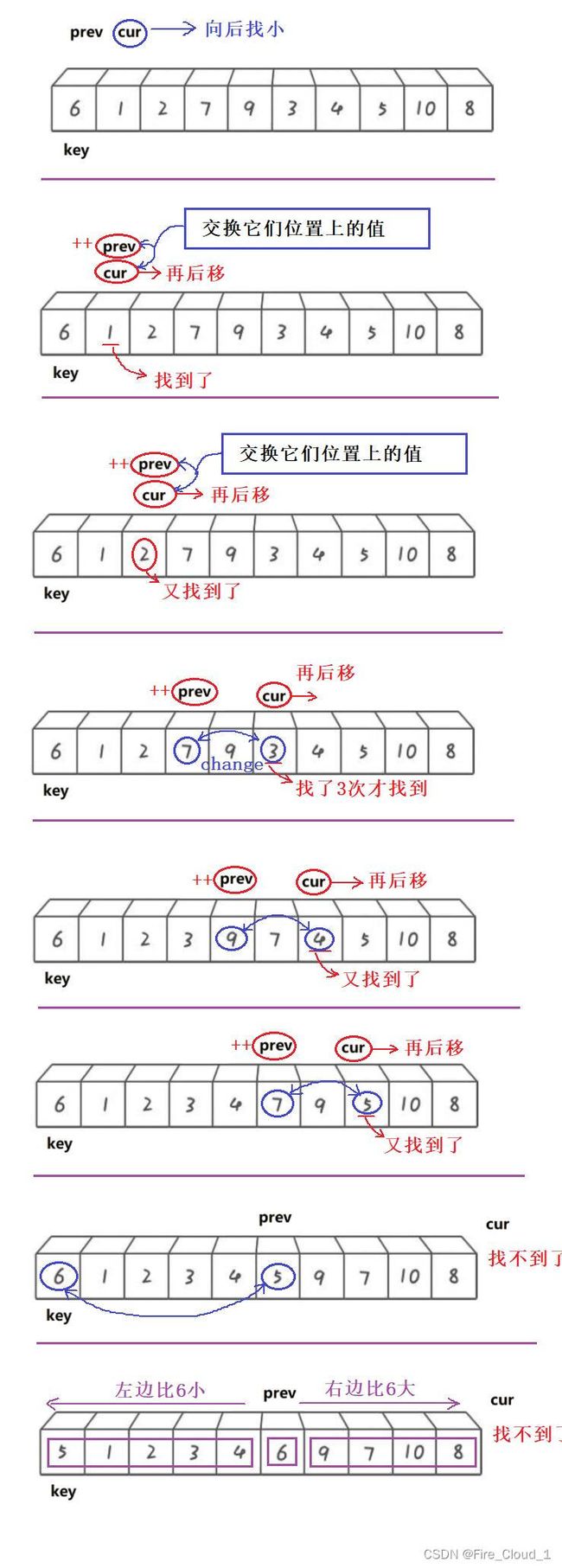
- 快速排序的最后一种方法是【前后指针法】,这种方法比较高效,但是有点晦涩难懂,因此我会分析得详细一些
- 下面是它的排序步骤
①定义一个prev指针位于起始端,再定义一个cur指针就位于它的后方,记录当前位置上的key值
②cur指针向后找比key小的值,若是找不到,则一直++;若是cur找到了比key小的值,prev++,然后交换二者的值之后cur再++
③直到cur超过右边界之后,退出循环逻辑,将此时prev位置上的值与key值做一个交换,保证左边比key小,右边比key大
3.3 算法分解图
- 一样也给出算法分解图帮助理解
3.4 代码展示与详解
- 首先展示一下代码
/*快速排序 —— 前后指针法*/
int PartSort3(int* a, int begin, int end)
{
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int prev = begin;
int cur = prev + 1;
int keyi = prev;
while (cur <= end)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
swap(&a[++prev], &a[cur]);
}
cur++; //cur无论如何都要++,因此直接写在外面
}
//cur超出右边界后交换prev处的值和key
swap(&a[keyi], &a[prev]);
return prev;
}
- 然后来讲解一下,主要的就是内部的这一个循环比较的逻辑。也就是将我们上面的思路转化为代码的形式,但是一定有同学疑惑这里为什么要加上
&& ++prev != cur呢,此时你可以返回去看上面的算法分解图,可以看到第一、二两次在交换swap(&a[++prev], &a[cur]);的时候,完全就没有动,因为它们是相同的,此时我们其实可以去做一个优化,那就是判断++prev之后的位置是否与cur是相同的,若是则不进行交换 - 而对于这里的比较是否大于进去以后交换的价值呢?因为对于这种比较的话其实CPU是可以直接操作的,运用一些与门、非门之类的;但是这里的交换呢,却需要使用到交换函数,我们知道调用函数就需要建立栈帧,而且在函数内部还要定义变量,此时我觉得这里是存在一些小小优化的,但是价值不大
- 但是有同学觉得这样的判断其实并没有很大的优化,确实是这样,但是呢这个思想我们要知道,因为在现今随着计算机的飞速发展,编译器对代码的优化已经达到了一个很大的程度,所以我们在Release版本下运行的时候其实是作了很大的优化。
while (cur <= end)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
swap(&a[++prev], &a[cur]);
}
cur++; //cur无论如何都要++,因此直接写在外面
}
- 最后的话当cur超出右边界之后交换prev和keyi上的值即可
swap(&a[keyi], &a[prev]);
4、三路划分法
上述三种是快速排序比较经典的方法,有关【三路划分法】某些高手针对快速排序的缺陷发明出来的一种方法,很是巧妙,所以这里给大家介绍一下
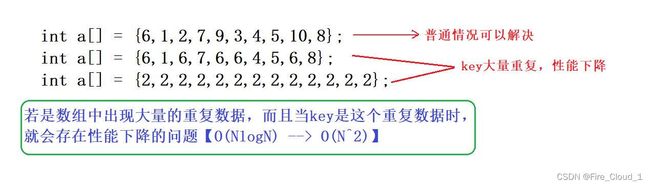
4.1 快速排序缺陷3——key值大量重复
- 在上面我们说到了快速排序存在缺陷的两个缺陷,现在再来说说它的一个缺陷。具体是什么呢?我们首先来分析一下
- 从上图可以看出,对于一般情况我们上面所介绍的三种方法都不会出现问题,但是对于一些特殊的极端情况而言,快速排序的效率就会明显下降,就如下面这样
- 对于数组中的数据都是重复的时候,此时在经历一次排序后key就会变得很极端,此时再对右区间去进行递归排序的时候又是一组很大的数据,在下一次选出key后就是1的位置,然后再接着递归下去就是一个很明显的O(N2)
4.2 算法思路简析
- 这就是快排的又一大缺陷,但是面对这种缺陷难道没办法了吗,那当然不会,民间存在很多的算法高手,有人就研究出来一种叫做【三路划分】的方法,修改了原本快速排序的结构,将原本的【两路划分】变成了三段小区间,如下图所示
- 对于这一种划分的算法逻辑是如何呢?
- 此处我们需要三个指针,一个【left】指向首端,一个【right】指向尾端,再一个【cur】指向left的后一个位置,对于【key值】也是一样取首端所在位置的值,因为我们会进行一个三数取中的操作
- 我们要做的就是通过将
a[cur]上的值与【left】和【right】上的值进行一个对比,然后将比key小的值扔到前面,将比key大的值扔到后面,若是和key相同则放到中间。在【left】与【cur】不断后移,【right】不断前移的过程中,三个区间就会很明显地被分化出来,直到cur > right时,便终止比较。接下去中间的这一块与key相等的值不需要去管他,我们只需要再去递归其左右区间即可,这就可以防止重复key值带来的多次递归的风险
4.3 代码详解与过程分解
代码展示
void QuickSortThreeDivisioin(int* a, int begin, int end)
{
if (begin >= end)
return; //最后递归下去区间不存在了,进行递归回调
//小区间优化
if ((end - begin + 1) < 15)
{
//在数据量少的时候改用直接插入排序
InsertSort(a + begin, end - begin + 1);
}
else
{
//三数取中
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int key = a[begin];
int left = begin;
int cur = left + 1;
int right = end;
while (cur <= right)
{
if (a[cur] < key)
{
swap(&a[left++], &a[cur++]);
}
else if (a[cur] > key)
{
swap(&a[cur], &a[right--]);
//此时cur不变化是因为从right换到中间的值可能还是比key大,为了在下一次继续进行比较
}
else
{
cur++;
}
}
//[begin, left - 1][left, right][right + 1, end]
QuickSortThreeDivisioin(a, begin, left - 1);
QuickSortThreeDivisioin(a, right + 1, end);
}
}
- 可以看到,大部分逻辑还是没有变化,就是修改了一下内部的排序过程而已。有了思路,写代码并不是什么难事
快速排序方法的“非递归写法”【校招要求✍】
递归的缺陷分析
看完了上面三种快速排序的,我们可以看出,都是使用递归的方法去实现的,也就是通过一层的遍历找出一个中间值,然后根据这个中间值进行一个左右划分,分别去进行分治递归。可以看出三种方法虽然类似,但都有自己的独特之处
但是大家肯定有一个疑问,既然都已经学了四种方法了,那为什么还要再去学习非递归的写法呢?我们来探究一下
- 刚才在分析快排的时间复杂度时,讲到了递归的缺陷,因为随着递归的层层深入,会建许多的栈帧,但若是建立的栈帧数量超出了编译器预留的栈空间大小,此时就会导致栈溢出【Stack Overflow】,这是栈溢出时最有可能的原因之一,相信大家在平时写代码的时候都有遇到过,不过这在平常我们做代码练习的时候还好,若是放到一些大的工程项目中可能就会导致一些大的问题。所以递归用起来虽然很香,但是呢很容易导致【爆栈】
- 递归的话是一层嵌套一层,一直递归到结束条件为止然后步步回调,看起来是很有思维逻辑,但是随着这个数据量的增大,递归的深度也会逐渐地加深。而且递归它是需要在栈空间中开辟栈帧的,在内存中,这个栈空间是很小的,大家可以进VS里看一下,默认的栈空间只有1M
- 所以如果这个数据量一旦增大的话,递归的深度也会不断加深,然后导致栈空间不够用,就导致了我们经常遇到的栈溢出问题【Stack Flow】—— 这就是递归的缺陷
- 所以,为什么说校招要考非递归这一块呢,就是想让你进企业后在有些数据量大的地方可以使用非递归来实现,因为在企业中开发的项目通常是很大的一个工程,都是直接面向用户的,所以这个数据量是很庞大的,如果我们用递归来实现,可能会给项目中安放一些致命的危险
非递归代码实现
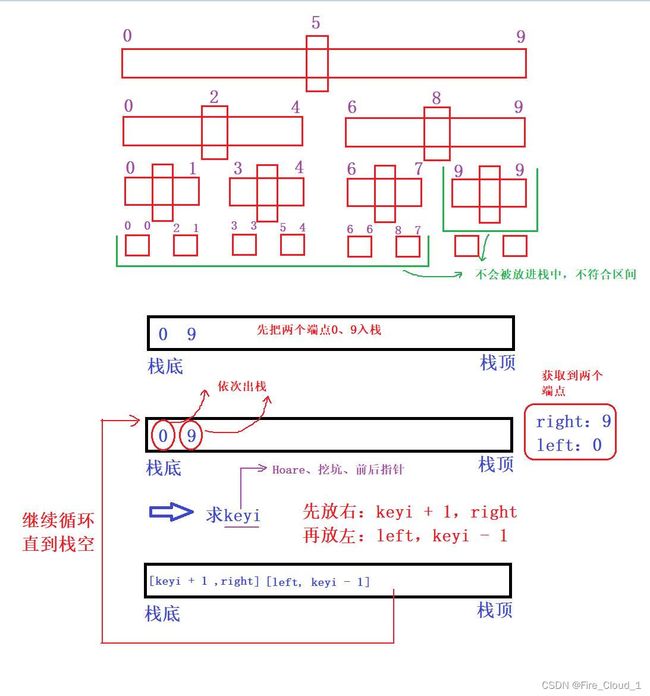
那非递归改递归这一块要怎么实现呢?我们来看一下
- 下面的递归转非递归是借助【数据结构栈】模拟递归的过程,其本质上还是递归的思想,只是换了个方式表达而已,非递归这一块的代码还是很重要的,可以先看一下
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
InitStack(&st);
//首先将整体区间入栈
PushStack(&st, begin);
PushStack(&st, end);
while (!StackEmpty(&st))
{
//出栈分别获取右左两个端点
int right = StackTop(&st);
PopStack(&st);
int left = StackTop(&st);
PopStack(&st);
//求解keyi的位置
int keyi = PartSort3(a, left, right);
//先入右
if (keyi + 1 < right)
{ //若是区间的值 > 1,则继续入栈
PushStack(&st, keyi + 1);
PushStack(&st, right);
}
//后入左
if (left < keyi - 1)
{ //若是区间的值 > 1,则继续入栈
PushStack(&st, left);
PushStack(&st, keyi - 1);
}
}
DestroyStack(&st);
}
- 我们再通过画图来看看
接下来稍微描述一下,主要是讲给还没有理解的同学
- 这里的内部循环始终要遵循的一条原则是栈的【先进后出】,此时看到要先将左右两个端点先入栈,然后在循环中,先取出栈顶的两个数据然后出栈,后入的便是右区间端点,先入的是做区间端点,分别用
right和left进行保存 - 然后将这个两个端点值通过上面所说到的三种快速排序的方法,使用单趟的一个逻辑,去求出每一次进来之后的keyi位置,然后再利用这个keyi进行一个左右区间的分化,也是一样的规则,先入右,后入左,但是在入栈之前要先判断一下当前这个区间的值的个数,若是只有一个数或者是这个区间根本就不存在的话,那就不需要再入了,若是区间的值> 1 就将这个区间入栈即可
- 最后循环往复执行这段逻辑,也就是一个递归的思维,直到递归完左区间之后递归右区间,最终到栈空为止表示没有区间需要在进行排序了
七、归并排序【⭐重点掌握⭐】
1、动图演示
2、算法思路简析
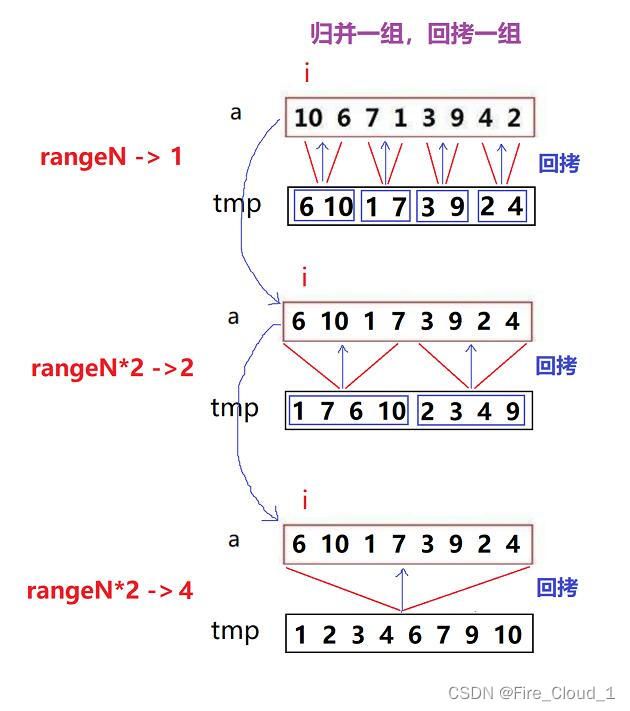
【核心思路】:分治思想。使原有的子序列合并,得到完全有序的序列,即先使每个子序列有序,再使子序列段间有序;
- 以下是有关归并排序的算法分解图,帮助理解
- 简要分析一下,上图是通过将原有的序列【10 6 7 1 3 9 4 2】分割成两部分,然后将这两部分再继续进行划分,再分割成两部分,一直划分直到区间的数组<=1为止,这就相当于是一个【递归】的过程,观察上半部分图,就是一棵二叉树,因此可理解为一直分解直到叶子结点为止
- 分解完成开始合并,原序列需要左区间有序,右区间有序,才可以对左右区间进行一个归并,因此从单个的小区间开始,慢慢向上回调进行归并(这里是画成了向下,可以参考二叉树的遍历),层层回调上来后左右区间再进行一个归并,最后得到一个有序的序列,这很像二叉树中的后序遍历,要其左子树、右子树都遍历完毕了,才去遍历根
有关归并排序会讲解【递归】和【非递归】两种解法,因为在校招中都会涉及
3、递归实现
3.1 思路分析
首先来说一下有关递归版本的实现思路分析
- 首先对于归并,无论是递归还是非递归,都需要去维护一个数组,因为在小区间进行归并的时候需要将归并完的数据暂时存放在一个tmp数组中,因此要维护一个数组是必不可少的。
- 因为归并和快排一样,都是需要进行不断递归的,所以对于不断分解和归并的过程需要单独封装为一个函数,然后需要传入边界值和两个数组(原数组、临时数组),接着在这个函数内部进行不断地递归划分直至这个序列有序。具体的我们放到代码中去讲解
3.2 代码详解
- 下面是MergeSort主函数,可以看到需要在堆区中开辟出一块空间去得到一个临时数组
- 中间则是分解归并的单独函数封装
- 最后则是对于这个临时开辟数组的释放(防止内存泄漏)以及指针置空(防止野指针)
void MergeSort(int* a, int n)
{
//开辟空间,存放归并后的数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("fail malloc");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp); //防止内存泄漏
tmp = NULL; //防止野指针
}
- 接下去子函数的讲解,下面是函数体的定义
void _MergeSort(int* a, int begin, int end, int* tmp)
- 接下去就是要通过每次传进来的区间端点值求解中间值,然后再通过这个中间值进行区间左右不断划分,进行递归调用,最后再进行一个回调
int mid = (begin + end) >> 1;
/*
* [begin, mid][mid + 1, end]
* --->继续进行子区间归并,相当于后序遍历【左,右,根】
*/
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
- 有递归,那一定要有递归出口,那就是当这个区间不存在的时候
if (begin >= end)
{
return;
}
- 当一个区间的左右子区间都递归完成后,就要对这两个区间进行一个归并的逻辑,首先看到定义的【i】,这个是用来遍历tmp这个临时数组的,因为tmp会一直存放数据,因此在下一次还要存放数据的时候就要从传进来的begin开始放置,因为begin是在不断变化的
- 然后就要去记录左右两个区间的端点值,因为这个mid是每次在变化的,加加减减不太方便,因此需要将四个端点值分别第一出来,这样去判断的时候就方便多了
- 接下去的话就是两个区间的数据不断比较的过程,放在一个while循环里,结束条件就是当一个区间已经遍历完毕之后就退出,因为当一个区间遍历完后,一个区间的所有数据和另一个区间一定全都比较过了,因此另一个区间剩下来的数据一定是大的那些数,所以在跳出循环后直接将某一段区间中还剩下的数据接到tmp数组之后就行
若是上面这段逻辑没有听懂,可以看看这篇文章,也是讲解有关归并逻辑的题解 ----> 合并两个有序数组
int i = begin; //i要从每次递归进来的begin开始放,可能是在右半区间
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//若是还有区间存在数据,表示没有归并完全,直接放入tmp即可
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
- 如果说以上的步骤是最核心的一步,那么下面的这句就是最关键的一步,因为每一次归并完后的数据都是存放在tmp临时数组里的,所以我们要将这些数据拷贝回原数组
- 因为我们每一次归并完都要去进行一个回拷的逻辑,所以每一次数组拷贝的起始位置和拷贝大小都是不一样的,这要根据分解的区间而定,可能是1个、2个、3个、4个不等,所以我们可以通过每次变更的【begin】和【end】进行一个控制,而对于【end - begin + 1】就是本次需要回拷的数组个数即数组大小
//最后将归并完后后的数据拷贝回原数组
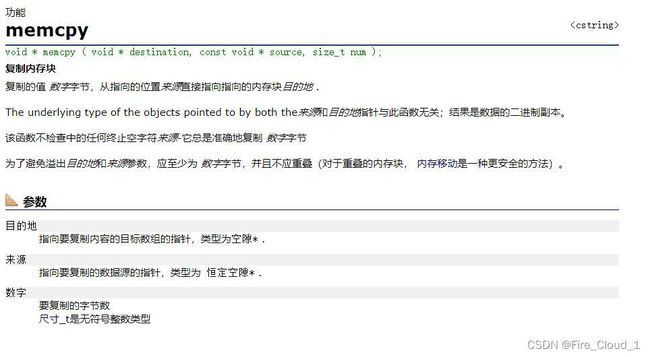
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
- 这是有关memcpy()这个函数的讲解,若是有不了解的小伙伴可以看一看
- 下面是整体代码的展示
void _MergeSort(int* a, int begin, int end, int* tmp)
{
//递归出口
if (begin >= end)
{
return;
}
int mid = (begin + end) >> 1;
/*
* [begin, mid][mid + 1, end]
* --->继续进行子区间归并,相当于后序遍历【左,右,根】
*/
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
int i = begin; //i要从每次递归进来的begin开始放,可能是在右半区间
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//若是还有区间存在数据,表示没有归并完全,直接放入tmp即可
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//最后将归并完后后的数据拷贝回原数组
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
/*归并排序*/
//时间复杂度:O(NlogN)
//空间复杂度:O(N)
void MergeSort(int* a, int n)
{
//开辟空间,存放归并后的数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("fail malloc");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp); //防止内存泄漏
tmp = NULL; //防止野指针
3.3 算法图解展示 && DeBug视频讲解【】
以下是递归分解算法图
以下是我录制的讲解视频(如果模糊就前后拖动一下)
归并排序递归版
4、非递归实现【校招要求✍】
说完递归,我们再来讲讲对于归并排序的非递归写法,重点在于理解递归写法,但是非递归校招也有要求,所以我会讲
4.1 思路分析
- 首先来看一下这一块的思路该如何实现,在快排那一部分我们是借助栈实现的非递归,那这里我们也可以使用栈吗❓,但是在这里使用栈或者队列这些数据结构都是很难实现的,需要去控制区间的出入。假设若是借助队列来实现的话,入了左区间、右区间之后,要获取到【左区间】的子区间,那就要进行出队,然后再入队,但是呢此时低头就变成了【右区间】。若是想获取到【左区间】的子区间,就需要将【右区间】出队然后才能获取到,此时若是还要在拿到其左右区间的话又要出队入队,此时就会变得非常复杂,代码写起来也是非常得难控制,所以我们果断舍弃这种写法
- 其实对于归并的非递归来说有一种很简单的思路,也不需要利用额外的数据结构,只需要使用一个变量每次取控制每次归并的区间大小即可,因为对于归并排序不像快速排序那样每次key值的位置都是随机的,对于归并排序来说每次归并的数量都固定的,要么是两两一归并、或者四四一归并,但是在后面的特殊情况中我们还需要单独考虑
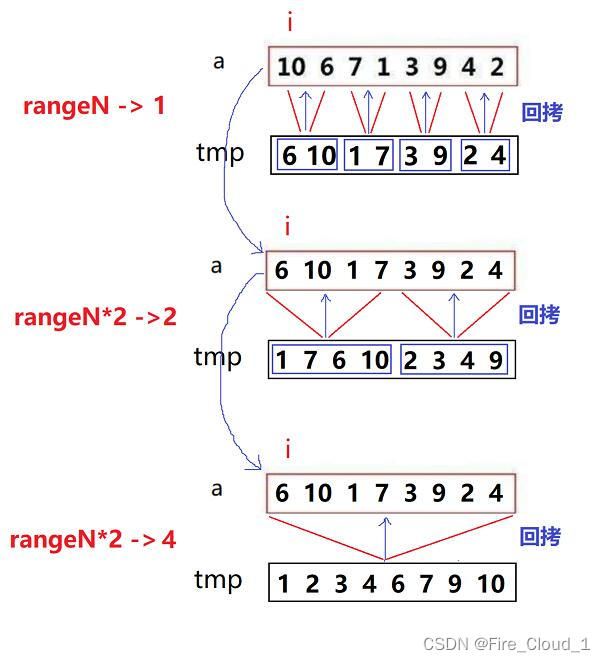
- 所以我们可以像下面这样去考虑,分为三次归并,首先是一一归并,使一个小区间中的两个数有序;然后两两归并,使一个小区间中的四个数有序;接下去四四归并,也就是使得正确区间有序。每一大组的归并放进一个循环中。但是每次要怎么使得刚好可以一一、两两、四四进行归并呢,这就需要使用到一个【rangeN】的变量来控制每次归并区间的大小了,具体如何控制我们放到代码中讲解
4.2 普通情况展示【可恶的随机数】
代码详解
- 接下去我们来说说该如何去实现上面这种写法呢,下面是单层循环的逻辑
int rangeN = 1;
for (int i = 0; i < n; i += 2 * rangeN)
{
int begin1 = i, end1 = i + rangeN - 1;
int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;
int j = i; //表示tmp每次都从上一次归并完放置后的地方开始
//归并...
//归并完一小组,拷贝一小组
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
// + i表示每次归并的组在发生变化 //因为end是最后落的位置,i是初始化位置,不会改变
}
- 当然最主要的还是这四个边界值,也就是每次归并的左右两个小区间的确定,需要通过本次的循环和标记值一起来确定
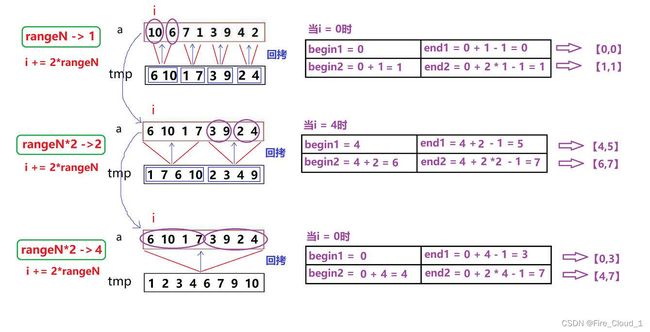
int begin1 = i, end1 = i + rangeN - 1;
int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;
- 这一块还是要自己手动去计算一下:
- 当rangeN = 1时算出来左右两个区间中是否只有一个数,也就是左右端点都相同;
- 当rangeN = 2时算出来左右两个区间中是否只有两个数,也就是左右端点相差1;
- 当rangeN = 4时算出来左右两个区间中是否只有四个数,也就是左右端点相差3;
- 以下是我做的一些计算
- 有了左右两个区间之后,就可以去进行【归并】了,这一块的逻辑我们在上面讲到过,因此直接复用即可。就是要重新换一个变量去接收每一趟循环中的i到哪里了,然后tmp数组也从哪里开始放置
int j = i; //表示tmp每次都从上一次归并完放置后的地方开始
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
//若是还有区间存在数据,表示没有归并完全,直接放入tmp即可
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
- 归并完后还是一样,要去进行一个回拷,因为这是内部单趟逻辑的回拷,因此也和递归那里一样,需要利用当前已知的变量进行一个精确定位,变量【i】即是当前开始的位置,而end2呢则是右区间结束的位置,也就是归并完成后的右端点位置
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
- 然后上面只是一个单组的逻辑,我们需要将其放在一个循环中,这个循环是用来控制rangeN值的
while (rangeN < n)
{
//单组的归并回拷逻辑
rangeN *= 2;
}
- 以下是上述所讲解的整体代码。这样程序就可以跑起来了
int rangeN = 1;
while (rangeN < n)
{
for (int i = 0; i < n; i += 2 * rangeN)
{
int begin1 = i, end1 = i + rangeN - 1;
int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;
printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
int j = i; //表示tmp每次都从上一次归并完放置后的地方开始
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
//若是还有区间存在数据,表示没有归并完全,直接放入tmp即可
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
//归并完一小组,拷贝一小组
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
// + i表示每次归并的组在发生变化 //因为end是最后落的位置,i是初始化位置,不会改变
}
rangeN *= 2;
}
//这两句别忘了加
free(tmp); //防止内存泄漏
tmp = NULL; //防止野指针
DeBug详细断位分析
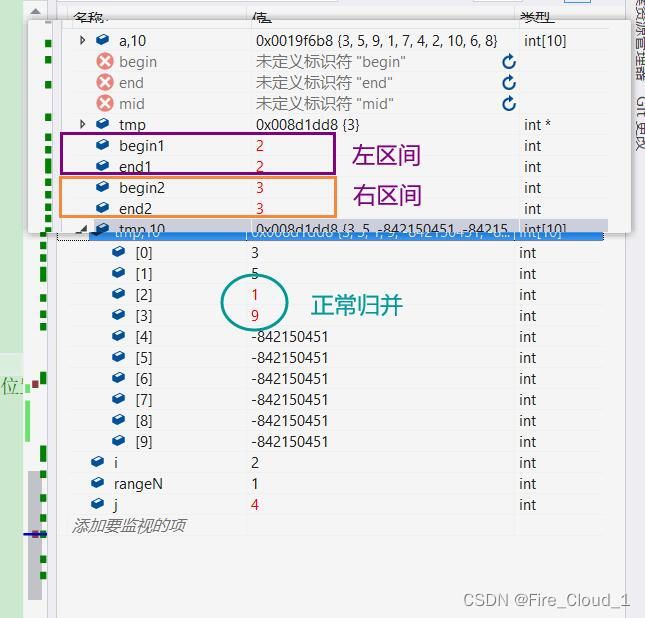
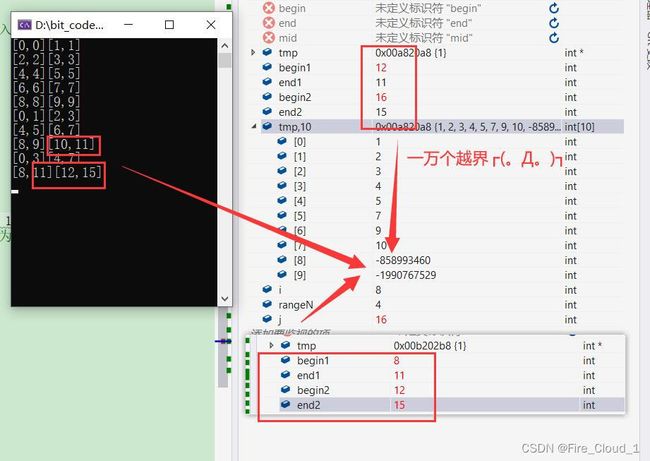
- 然后我们使用这一段代码去进行一个测试,这里我放置了两个案例,一个是8个数,一个是10个数。为了可以精确地观测到左右区间的四个端点值,我们加上这一句话将单次的循环打印出来
printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
- 可以看到对于下面这种测试案例没有问题。接着我们再来看一个
- 可以看到,对于10个数的情况,出现了一些越界的端点值,所以程序就崩溃了
- 我们再通过DeBug调试来看看
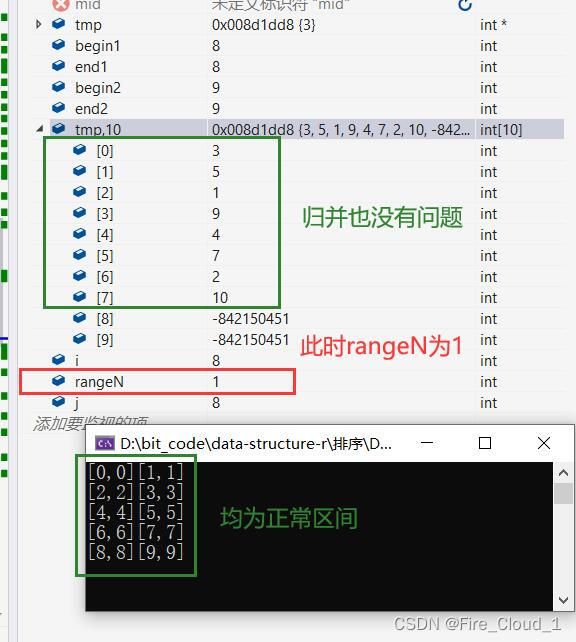
- 可以看到当range为1的时候,也就是一一进行归并时,不会出现越界的问题
- 此时我们进入下一层归并的逻辑,让rangeN变为2
- 但是接下来再运行,就会出现问题了
- 然后再下去,就一发不可收拾了
- 可以看出,越界是一个很大的问题,在下一模块中,我将针对越界的情况做一个讲解
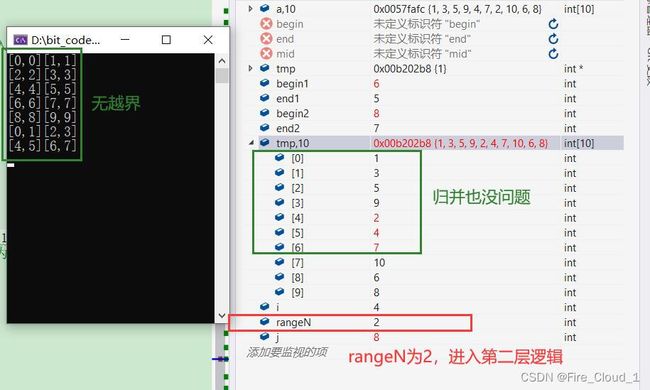
4.3 越界的特殊情况考虑
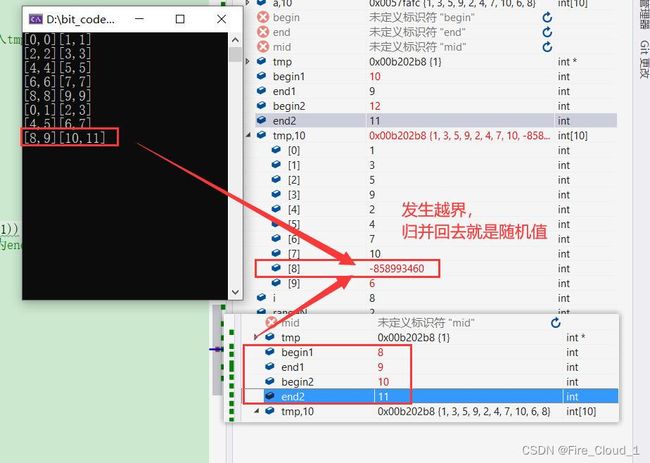
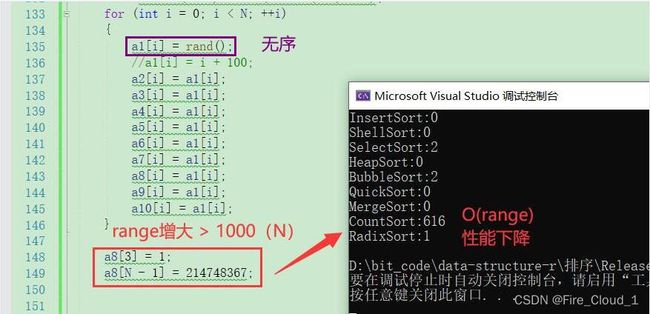
通过上一模块中的层层的DeBug调试,我们看到了 当rangeN = 2,也就是两两一归并的时候出现了越界的情况,为什么会发生这样的事情呢?记得我在一开始的时候有说过,对于归并排序,和快速排序不一样的地方在于,其每次两个区间大小是确定的,若是左半区间有四个数,那么右半区间的大小也必须要能够存放得下四个数
所以当待排序的数字有十个的时候,两两一归并,当前面八个归并完成后,后面的两个自动作为左半区间,那么此时右半区间就会产生越界的情况,在数组章节我们有讲到过,若是出现越界的情况就会出现随机值
解决方案 —> 一 一分析越界的几种情况,然后对其分别做考虑判断

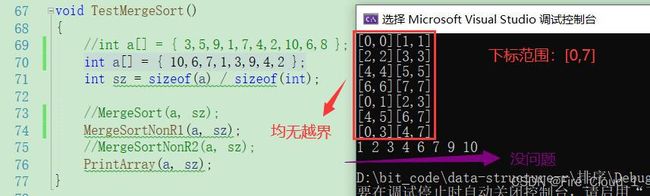
4.3.1 方法一【不修边界——部分拷贝】
- 下面这种是处理越界的第一种方法,就是不做边界修正,若是碰见有越界的情况直接break出当前小组的循环,也就是不进行归并的逻辑
/*
* 处理越界的情况
*/
if (end1 >= n) {
break;
}
else if (begin2 >= n) {
break;
}
else if (end2 >= n) {
end2 = n - 1; //end2越界要修正一下,不可以break,因为最后需要求整个数组的长度
}
- 此时我们需要去做一个部分的拷贝,也就是归并一部分拷贝一部分,若是做整体拷贝的话当越界的情况break出来进行拷贝回去之后原先a数组中的值就会被覆盖掉
//归并完一小组,拷贝一小组
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
// + i表示每次归并的组在发生变化 //因为end是最后落的位置,i是初始化位置,不会改变
4.3.2 方法二【修边界——整体拷贝】
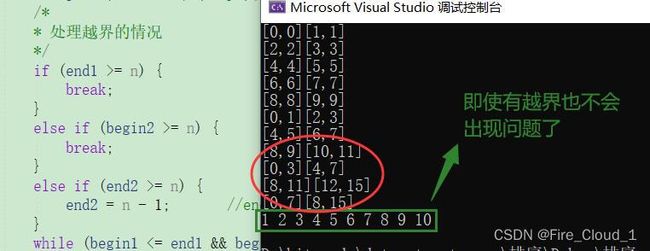
- 第二种是整体拷贝,当一层的逻辑执行完后,所有的小组都归并完成了,此时再去进行一个整体回拷的逻辑,因为这个时候我们在遇到越界的问题时需要对边界去做一个修正,当修正完之后也就不会出现问题了
- 我们来看一下这种情况该如何修正,很简单:
- 若是就右端点越界的话只需要将其修正为数组下标的最后一个位置即可;
- 若是整个区间都越界了,那就修改一下【begin】 > 【end】即可;
/*
* 处理越界的情况
*/
if (end1 >= n) {
end1 = n - 1;
begin2 = n; //begin2要比end2来的大,才不构成区间
end2 = n - 1;
}
else if (begin2 >= n) {
begin2 = n; //begin2要比end2来的大,才不构成区间
end2 = n - 1;
}
else if (end2 >= n) {
end2 = n - 1;
}
- 若是要整体回拷的话
memcpy(a, tmp, sizeof(int) * n);就要放在单层循环外了,可以看到每次拷贝的区间大小都是固定的 - 来看一下这种情况的算法分解图。可以看到,就是当当层的逻辑全部走完之后再进行的一个整体回拷
- 接下去来看看修正后的运行结果
4.4 小结
可以看到,对于归并排序来说,无论是递归还是非递归,都是存在一定难度的,特别是对于归并的非递归这一块,光边界修正这一块就让人头大(((φ(◎ロ◎;)φ))),但是大家还是要有所掌握,上面说过,对于一些场景使用非递归要比递归来的安全很多
上述的七个排序均为比较类排序,接下去我们来介绍三种非比较类排序
八、计数排序【还是不错的】
1、动图演示
2、算法思路简析
【核心思路】:通过统计相同元素出现次数,存放到一个数组中,然后再根据统计的结果将序列回收到原来的序列中
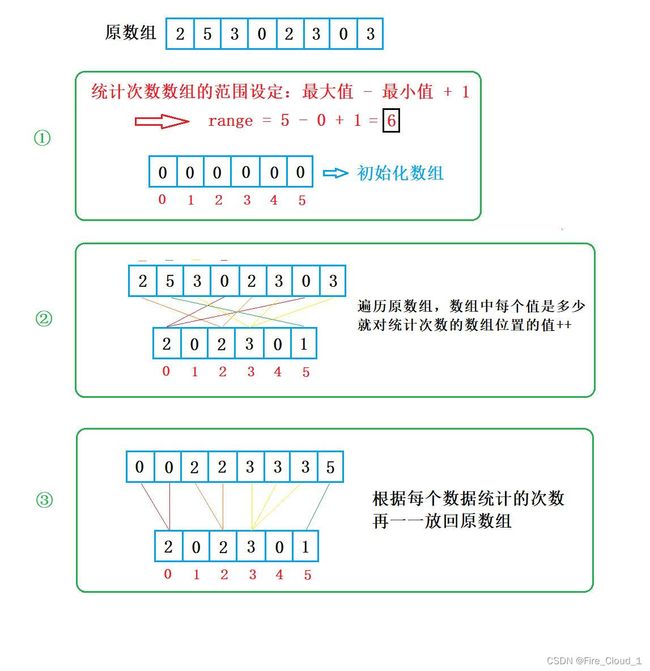
- 然后我们来看一下有关计数排序的大体步骤,我是分为以下三步
3、具体代码分析
接下去讲刚才分析的思路转化为代码
①开辟统计次数的数组
- 因为我们要开辟统计次数的数组,但是不知道开多大,所以应该先去找出数组中的最大值与最小值,然后求出range【范围】
//1.找出数组中的最大值和最小值,然后开辟统计数组
int min = a[0];
int max = a[0];
for (int i = 0; i < n; ++i)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
- 有了最大最小值之后,就可以去求解范围了,这个范围即是数组的大小。
- 在开出数组之后,记得对其进行一个初始化,也就是使用memset将所有位上的数都设置为0
int range = max - min + 1; //数据范围
int* CountArray = (int*)malloc(sizeof(int) * range);
memset(CountArray, 0, sizeof(int) * range); //初始化数组均为0
②遍历原数组,统计出每个数字出现的次数,将其一一映射到CountArray数组中
//2.统计数组中每一个数出现的个数,映射到CountArray数组中
for (int i = 0; i < n; ++i)
{
CountArray[a[i] - min]++;
//a[i] - min 表示找出相对位置
}
- 重点说一下这个
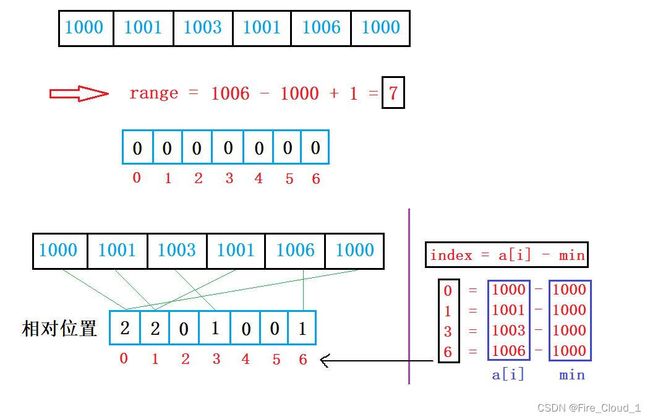
a[i] - min是什么意思,对于我在上一模块展示的只是一个特殊情况,最小值是从0开始的,刚好可以和CountArray数组中的下标对上,但是对于大多数的情况来说,最小值不会是0,所以在一一映射的过程中就需要做一些变化
- 可以看到,上面这种情况的最小值就为1000, range的求解还是一个套路,但是对于映射就不一样了,因为我们开出的数组下标只有0~6,所以此时我们要使用一个【相对位置】去算出每个数字对应的位置,使用
a[i] - min即可
③根据每个数字统计完后的次数,一一放回原数组
- 刚才使用
a[i] - min映射到了CountArray数组,现在我们要将其再一一放回去,此时你就会发现数组便会呈现有序 - 但是这要怎么放回去呢,首先外层先去遍历这个CountArray数组,内层的while循环表示每一个数字对应的要放回几次
- 接下去要考虑的问题就是如果通过这个下标去还原回原先的数字,刚才我们减了min,现在加回去即可
j + min
//3.将统计数组中的数写回原数组中,进行排序
int index = 0;
for (int j = 0; j < range; ++j)
{
//根据统计数组去找出每个数要写回几次
while (CountArray[j]--)
{
a[index++] = j + min;
//每次循环中的j不会发生变化,加上最小值可以找回原来的数字
}
}
整体代码展示
/*计数排序*/
void CountSort(int* a, int n)
{
//1.找出数组中的最大值和最小值,然后开辟统计数组
int min = a[0];
int max = a[0];
for (int i = 0; i < n; ++i)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int range = max - min + 1; //数据范围
int* CountArray = (int*)malloc(sizeof(int) * range);
memset(CountArray, 0, sizeof(int) * range); //初始化数组均为0
//2.统计数组中每一个数出现的个数,映射到CountArray数组中
for (int i = 0; i < n; ++i)
{
CountArray[a[i] - min]++;
//a[i] - min 表示找出相对位置
}
//3.将统计数组中的数写回原数组中,进行排序
int index = 0;
for (int j = 0; j < range; ++j)
{
//根据统计数组去找出每个数要写回几次
while (CountArray[j]--)
{
a[index++] = j + min;
//每次循环中的j不会发生变化,加上最小值可以找回原来的数字
}
}
}
运行结果
- 刚才说到的两种情况都展示一下
4、复杂度分析
来看看计数排序的时空复杂度
【时间复杂度】:O(N + range)
【空间复杂度】:O(range)
- 首先对于时间复杂度而言,有同学就看不懂这个【N + range】是什么意思,观看代码看出我们遍历了两遍原数组和一遍统计个数的数组,对于2N可以简化成N,因此就是【N + range】,完全是要看这个CountArray数组的大小是多少,若是
- range <= N ——> O(N + N) = O(N)
- range > N ——>O(N + range) = O(range)
- 对于空间复杂度也是取决于这个CountArray数组的大小,便是O(range)
对于计数排序而言,因为需要统计数据出现的次数,所以只能用与整型的数据,如果是浮点数或字符串排序还得用比较排序
九、桶排序【局限性大】
1、动图演示
2、算法思路简析
看了上面的通动图之后,你应该对桶排序有了以及基本的认识,接下去我们一起来了解一下如何使用【桶】来进行排序
- 排序的思路很简单,就是将待排序的数组中每一个数根据他们的范围一一放入对应的桶中,然后在每一个桶的内部分别对其进行排序,在每个桶都排完序之后,再从第一个桶开始,将其中的数据一一放回原数组即可
- 以下是算法分解图
![]()
3、代码详解与分析
- 首先我们需要定义出桶以及每个桶中的计数器
int bucket[5][5]; // 分配五个桶。
int bucketsize[5]; // 每个桶中元素个数的计数器。
- 接下去使用memset()对其进行初始化
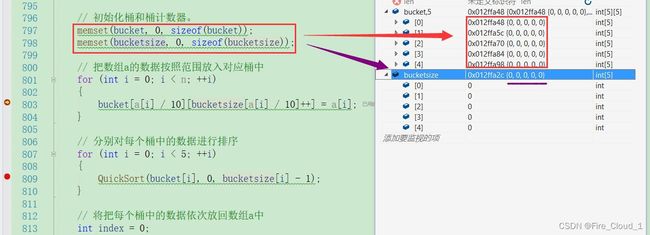
// 初始化桶和桶计数器。
memset(bucket, 0, sizeof(bucket));
memset(bucketsize, 0, sizeof(bucketsize));
- 接下来的工作是最重要的一步,那就是将数组a中的内容数据一一放入对应的桶中
- 这里的桶我开的是一个二维数组,行记录的是数据,列记录的是该桶中数据的个数,分别对每个数据进行整除10就可以刚好让其落入对应的桶中,你可以自己去算算
// 把数组a的数据按照范围放入对应桶中
for (int i = 0; i < n; ++i)
{
bucket[a[i] / 10][bucketsize[a[i] / 10]++] = a[i];
}
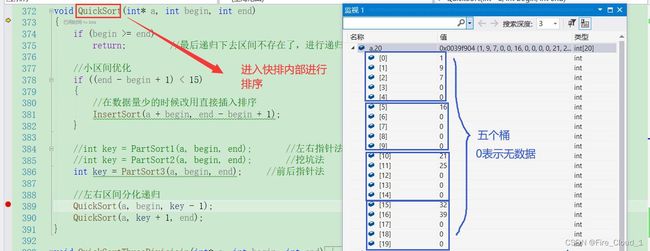
- 接下去的话就是对每个桶中的数据进行排序了,我们可以使用上面学过的一些内部排序,这里我选择使用【快速排序】
// 分别对每个桶中的数据进行排序
for (int i = 0; i < 5; ++i)
{
QuickSort(bucket[i], 0, bucketsize[i] - 1);
}
- 最后一步的话就是将每个桶中对应的数据依次放回数组中即可
// 将把每个桶中的数据依次放回数组a中
int index = 0;
for (int i = 0; i < 5; ++i)
{
for (int j = 0; j < bucketsize[i]; ++j)
{
a[index++] = bucket[i][j];
}
}
整体代码展示
/*桶排序*/
void BucketSort(int* a, int n)
{
int bucket[5][5]; // 分配五个桶。
int bucketsize[5]; // 每个桶中元素个数的计数器。
// 初始化桶和桶计数器。
memset(bucket, 0, sizeof(bucket));
memset(bucketsize, 0, sizeof(bucketsize));
// 把数组a的数据按照范围放入对应桶中
for (int i = 0; i < n; ++i)
{
bucket[a[i] / 10][bucketsize[a[i] / 10]++] = a[i];
}
// 分别对每个桶中的数据进行排序
for (int i = 0; i < 5; ++i)
{
QuickSort(bucket[i], 0, bucketsize[i] - 1);
}
// 将把每个桶中的数据依次放回数组a中
int index = 0;
for (int i = 0; i < 5; ++i)
{
for (int j = 0; j < bucketsize[i]; ++j)
{
a[index++] = bucket[i][j];
}
}
}
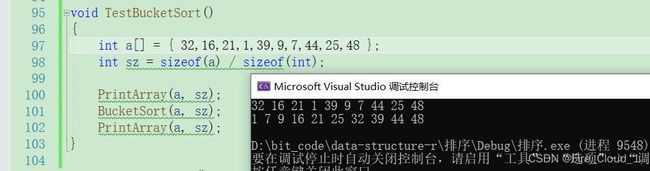
运行结果
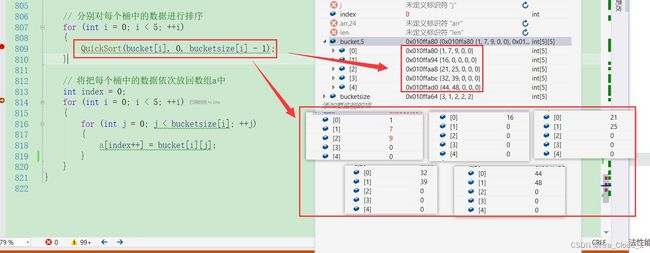
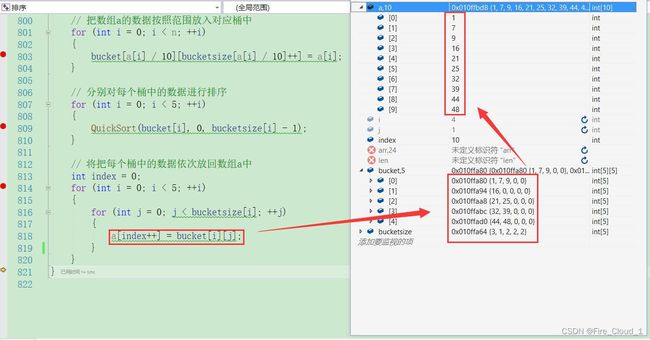
4、DeBug调试分析
这一环节我们跟着调试信息一步步地;来分析一下
- 首先是对于数组的初始化
-
接下去展示数据放入对应的桶中,这里我们通过视频来观看
-
接下去就是对每个桶中的数据进行排序
- 最后将每个桶中的数据一一放回去即可
5、复杂度分析
【时间复杂度】:O(K + N)
【空间复杂度】:O(K + N)
- 这一块后面再做更新。。。还在搜寻资料中
十、基数排序【不常用】
1、动图演示
2、算法思路分析
是的,你没有看错,除了【计数排序】之外,还有一个叫做【基数排序】的,不过它和计数排序可完全不同。它是桶排序的升级版
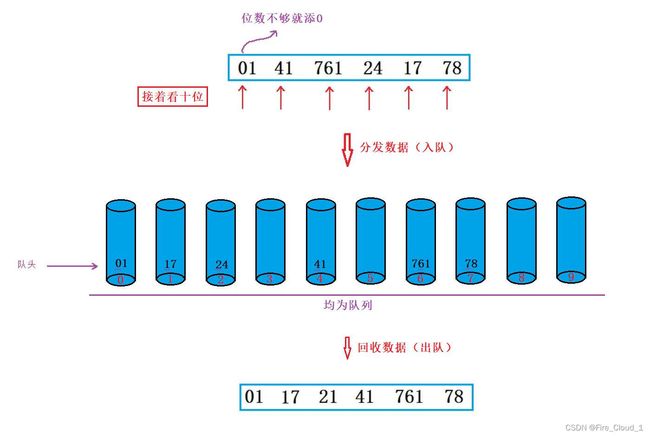
- 对于基数排序而言,它的原理就是【基于数位来排序】,什么是数位呢?也就是我们常说的个位、十位、百位
- 首先我们要去取到每个数的个位,通过观测它们的个位,将一 一放入对应的桶中,那此时我们就需要一些桶。因为每次是都是取一个数,所以我们需要十个桶【0~9】,但是这些桶不是一般的桶,而是要为一个链表或者队列,因为要实现先分发入桶中的数据先回收出来,因为是一个【FIFO】的原理,所以这里我们优先采用队列,当然你想要使用链表也是可以的了,那么 【分发数据】就是【尾插】,【回收数据】就是【头删】
- 有了这些桶之后,那就方便多了,此时只需要看个位的数字是多少,然后一一链接上去即可。接下去就是去比较各个数字十位或者百位的数据,当然这要取决于整组数据中位数最大的那个数字,所以在分发数据前我们应该先去求出这些数中最大的那个数,然后再求出这个数的位数,那它的位数多少位,那就需要比较多少论
3、代码分析与算法图解
- 有了基本的思路之后,接下去我们先来看看大体的运行流程
①第一轮(个位的比较)
②第二轮(十位的比较)
③第三轮(百位的比较)
- 好,看了这三轮比较之后,相信你对基数排序的大体流程有了一个更加全面的了解,接下去我们将上面所说的内容转化为代码的形式
- 首先要去做一些准备工作。也就是把桶定义出来,桶的个数我们固定为10个,因为【0~9】这个十个数字都有可能会出现。这桶的底层结构使用的是C++STL中的队列容器,如果不了解的看这个 --> C++STL容器详解
#include - 接下去就是主体代码
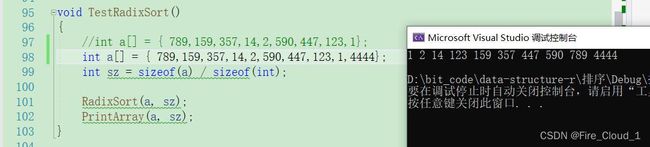
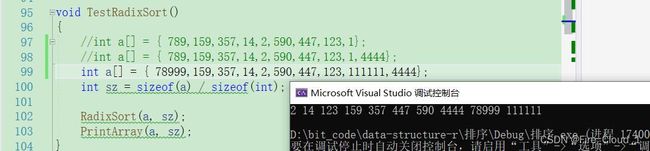
void RadixSort(int* a, int n)
{
//首先求出数组中的最大值
int max = GetMax(a, n);
//求出最大值的位数
int k = GetDigit(max);
//进行k次的数据分发和回收
for (int i = 0; i < k; ++i)
{
//分发数据
Distribute(a, n, i);
//回收数据
Collect(a);
}
}
求解数组中的最大值
//求解数组中的最大值
int GetMax(int* a, int n)
{
int max = a[0];
for (int i = 0; i < n; ++i)
{
if (a[i] > max)
max = a[i];
}
return max;
}
求解最大值的位数
//求解最大值的位数
int GetDigit(int num)
{
//num : 10000
int count = 0;
while (num > 0)
{
count++;
num /= 10;
}
return count;
}
获取位数位逻辑
//value: 789
// k: 0
int GetKey(int value, int k)
{
int key = 0;
while(k >= 0)
{
key = value % 10;
value /= 10;
k--;
}
return key;
}
分发数据逻辑
获取key之后,q[key]即为每一个桶。使用push往里入数据
//分发数据
void Distribute(int* a, int n, int k)
{
for (int i = 0; i < n; ++i)
{
int key = GetKey(a[i], k);
qu[key].push(a[i]);
}
}
回收数据逻辑
接着一一获取每个桶中的头部数据,放回数组中,然后出队该数据即可
//回收数据
void Collect(int* a)
{
int index = 0;
for (int i = 0; i < RADIX; ++i)
{
while (!qu[i].empty())
{
a[index++] = qu[i].front();
qu[i].pop();
}
}
}
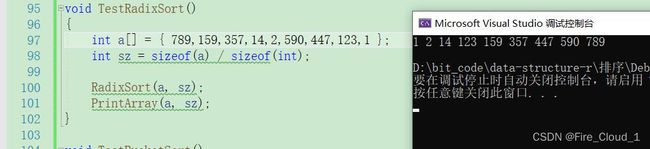
运行结果
- 可以灵活地找出数组中的最大值后,我们可以测试所有的案例
4、复杂度分析
【时间复杂度】:O(K * N)
【空间复杂度】:O(K + N)
- 可以看到,对于基数排序的时间复杂度而言,我们通过观察代码可以看出,主函数有一个K层的外循环,然后里面套了两层循环,对于【分发数据】中,需要去遍历一遍原数组,这里就有O(N)了,然后执行K次去找到那个Key值,这个为常数次可以忽略,接下去对于【回收数据】而言,只运行了RADIX次,也为常数阶可以忽略,这么看下来只剩外层的一个K层循环套一个内层的O(N),因此可以看出其时间复杂度为O(K * N)
- 对于基数排序空间复杂度应该为O(K + N)
拓展:文件外排序【了解一下】
排序这一块,除了对内部的数据进行排序,很多场合下还会对文件中的数据去进行一个排序,而对于文件外排序这一块,我们主要使用上面所学的归并排序来完成
1、前言
- 对于文件中的数据,一般都是很大的,不像我们上面所讲的十二十个数,可能会有成千上百的数据需要我们去排序,此时效率最高的就是【归并排序】了,因为面对海量的数据而言,像效率较高的【快速排序】需要克服三数取中的困难,还有像【堆排序】【希尔排序】这些,都无法支持随机访问,所以很难去对大量的文件进行一个排序,速度会非常之慢。即使是有文件函数【fseek()】这样的函数可以使文件指针偏移,还是很难做到高效。因为磁盘的速度比起内存差了太多太多了,具体的我不太清楚大概有差个几千倍这样,
- 所以我们就想到了【归并排序】,它既是内排序,也是外排序,而且性能也不差,算是速度较快的几个排序之一了。但是要如何进行归并呢?
2、思路解析
![]()
- 回忆一下归并排序的原理,就是两个有序区有序,然后两两一归才使得整体可以有序,如果左右都无需,那么继续对其进行左右分割归并
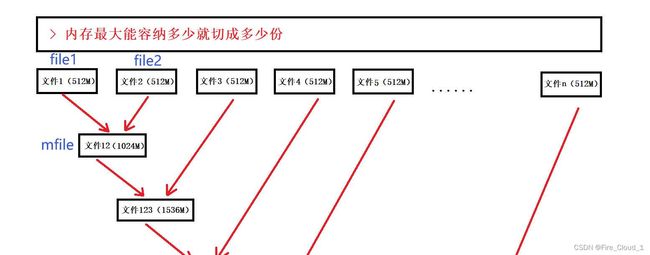
- 但是本次,我要教给你的你是另外一种思路:
将一个大文件平均分割成N份,保证每份的大小可以加载到内存中,然后使用快排将其排成有序再写回一个个小文件,此时就拥有了文件中归并的先决条件
- 具体示意图如下

这里我设置一个这样的规则,令文件1为【1】,文件2位【2】,它们归并之后即为【12】,然后再让【12】和文件3即【3】归并变成【123】,以此类推,所以最后归出的文件名应该是【12345678910】
3、代码详解
下面是大文件分割成10个小文件的逻辑,首先来讲解一下这块,代码中很多内容涉及到文件操作,如果有文件操作还不是很懂的小伙伴记得再去温习一下
- 整体的逻辑就在于从文件中读取100个数据,但是分批进行读取,每次首先去读9个数,然后当读到第十个数的时候,先将其加入数组中,然后再对数组中的这10个数进行排序。排完序后就将这个10个数通过文件指针再写到一个小文件中
- 接着当第二次循环上来的时候,就开始读第11~20个数;以此往复,直到读完这个100个数为止,那此时我们的工程目录下就会出现10个小文件,就是对这100个数的分隔排序后的结果
void MergeSortFile(const char* file)
{
FILE* fout = fopen(file, "r");
if (!fout)
{
perror("fopen fail");
exit(-1);
}
int num = 0;
int n = 10;
int i = 0;
int b[10];
char subfile[20];
int filei = 1;
//1.读取大文件,然后将其平均分成N份,加载到内存中后对每份进行排序,然后再写回小文件
memset(b, 0, sizeof(int) * n);
while (fscanf(fout, "%d\n", &num) != EOF)
{
if (i < n - 1)
{
b[i++] = num; //首先读9个数据到数组中
}
else
{
b[i] = num; //再将第十个输入放入数组
QuickSort(b, 0, n - 1); //对其进行排序
sprintf(subfile, "%d", filei++);
FILE* fin = fopen(subfile, "w");
if (!fin)
{
perror("fopen fail");
exit(-1);
}
//再进本轮排好序的10个数以单个小文件的形式写到工程文件下
for (int j = 0; j < n; ++j)
{
fprintf(fin, "%d\n", b[j]);
}
fclose(fin);
i = 0; //i重新置0,方便下一次的读取
memset(b, 0, sizeof(int) * n);
}
}
- 我们来看一下排序的结果
![]()
- 将大文件分成10个小文件后,接下去就是要对这个10个小文件进行归并,具体规则我上面已经说了
- 下面就是单趟归并的逻辑的,就和我们上面说到的归并排序的代码是很类似的,只不过这里是文件的操作而已。要注意的是对于文件来说是有一个文件指针的,若是你读取了一个之后那么文件指针这个结构体中的数据标记就会发生变化,标记为当然所读内容的下一个了
- 所以我们不能将读取读取小文件中的数据的操作放在while循环中,应该单独将其抽离出来进行判断才才对。若是哪个文件中的数小,那么就将这个数写到新的【mfile】文件中去,然后继续读取当前文件的后一个内容
//文件归并逻辑
void _MergeSortFile(const char* file1, const char* file2, const char* mfile)
{
FILE* fout1 = fopen(file1, "r");
if (!fout1)
{
perror("fopen fail");
exit(-1);
}
FILE* fout2 = fopen(file2, "r");
if (!fout2)
{
perror("fopen fail");
exit(-1);
}
FILE* fin = fopen(mfile, "w");
if (!fin)
{
perror("fopen fail");
exit(-1);
}
int num1, num2;
//返回值拿到循环外来接受
int ret1 = fscanf(fout1, "%d\n", &num1);
int ret2 = fscanf(fout2, "%d\n", &num2);
while (ret1 != EOF && ret2 != EOF)
{
if (num1 < num2)
{
fprintf(fin, "%d\n", num1);
ret1 = fscanf(fout1, "%d\n", &num1);
}
else
{
fprintf(fin, "%d\n", num2);
ret2 = fscanf(fout2, "%d\n", &num2);
}
}
while (ret1 != EOF)
{
fprintf(fin, "%d\n", num1);
ret1 = fscanf(fout1, "%d\n", &num1);
}
while (ret2 != EOF)
{
fprintf(fin, "%d\n", num2);
ret2 = fscanf(fout2, "%d\n", &num2);
}
fclose(fout1);
fclose(fout2);
fclose(fin);
}
最后在打开文件后不要忘了将文件关闭哦,不然就白操作了
- 当然上面是一个单趟的逻辑,我们还要对【file1】【file2】【mfile】进行一个迭代
//利用互相归并到文件,实现整体有序
char file1[100] = "1";
char file2[100] = "2";
char mfile[100] = "12";
for (int i = 2; i <= n; ++i)
{
_MergeSortFile(file1, file2, mfile);
//迭代
strcpy(file1, mfile);
sprintf(file2, "%d", i + 1);
sprintf(mfile, "%s%d", mfile, i + 1);
}
- 大概就是这么一个迭代的过程
整体代码展示
//文件归并逻辑
void _MergeSortFile(const char* file1, const char* file2, const char* mfile)
{
FILE* fout1 = fopen(file1, "r");
if (!fout1)
{
perror("fopen fail");
exit(-1);
}
FILE* fout2 = fopen(file2, "r");
if (!fout2)
{
perror("fopen fail");
exit(-1);
}
FILE* fin = fopen(mfile, "w");
if (!fin)
{
perror("fopen fail");
exit(-1);
}
int num1, num2;
//返回值拿到循环外来接受
int ret1 = fscanf(fout1, "%d\n", &num1);
int ret2 = fscanf(fout2, "%d\n", &num2);
while (ret1 != EOF && ret2 != EOF)
{
if (num1 < num2)
{
fprintf(fin, "%d\n", num1);
ret1 = fscanf(fout1, "%d\n", &num1);
}
else
{
fprintf(fin, "%d\n", num2);
ret2 = fscanf(fout2, "%d\n", &num2);
}
}
while (ret1 != EOF)
{
fprintf(fin, "%d\n", num1);
ret1 = fscanf(fout1, "%d\n", &num1);
}
while (ret2 != EOF)
{
fprintf(fin, "%d\n", num2);
ret2 = fscanf(fout2, "%d\n", &num2);
}
fclose(fout1);
fclose(fout2);
fclose(fin);
}
/*文件外排序*/
void MergeSortFile(const char* file)
{
srand((unsigned int)time(NULL));
FILE* fout = fopen(file, "r");
if (!fout)
{
perror("fopen fail");
exit(-1);
}
//先写100个随机数进文件
//for (int i = 0; i < 100; ++i)
//{
// int num = rand() % 100;
// fprintf(fout, "%d\n", num);
//}
int num = 0;
int n = 10;
int i = 0;
int b[10];
char subfile[20];
int filei = 1;
//1.读取大文件,然后将其平均分成N份,加载到内存中后对每份进行排序,然后再写回小文件
memset(b, 0, sizeof(int) * n);
while (fscanf(fout, "%d\n", &num) != EOF)
{
if (i < n - 1)
{
b[i++] = num; //首先读9个数据到数组中
}
else
{
b[i] = num; //再将第十个输入放入数组
QuickSort(b, 0, n - 1); //对其进行排序
sprintf(subfile, "%d", filei++);
FILE* fin = fopen(subfile, "w");
if (!fin)
{
perror("fopen fail");
exit(-1);
}
//再进本轮排好序的10个数以单个小文件的形式写到工程文件下
for (int j = 0; j < n; ++j)
{
fprintf(fin, "%d\n", b[j]);
}
fclose(fin);
i = 0; //i重新置0,方便下一次的读取
memset(b, 0, sizeof(int) * n);
}
}
//利用互相归并到文件,实现整体有序
char file1[100] = "1";
char file2[100] = "2";
char mfile[100] = "12";
for (int i = 2; i <= n; ++i)
{
_MergeSortFile(file1, file2, mfile);
//迭代
strcpy(file1, mfile);
sprintf(file2, "%d", i + 1);
sprintf(mfile, "%s%d", mfile, i + 1);
}
}
运行结果展示
整体代码展示
本次的代码较以往都多了许多,因为是集结了所有的排序算法还有案例测试、性能测试相关的代码,都给到大家
sort.h
#pragma once
#include sort.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "sort.h"
#include "stack.h"
//#define K 3 //表示数字的位数
#define RADIX 10 //表示桶的个数(固定)
queue<int> qu[RADIX]; //定义基数(每个基数均为一个队列)
/*打印*/
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
/*交换*/
void swap(int* x, int* y)
{
int t = *x;
*x = *y;
*y = t;
}
/*直接插入排序*/
void InsertSort(int* a, int n)
{
//不可以< n,否则最后的位置落在n-1,tmp访问end[n]会造成越界
for (int i = 0; i < n - 1; ++i)
{
int end = i;
int tmp = a[end + 1]; //将end后的位置先行保存起来
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end]; //比待插值来得大的均往后移动
end--; //end前移
}
else
{
break; //若是发现有相同的或者小于带插值的元素,则停下,跳出循环
}
}
a[end + 1] = tmp; //将end + 1的位置放入保存的tmp值
}
}
//void ShellSort(int* a, int n)
//{
// int gap = n / 2;
//
// for (int j = 0; j < gap; ++j)
// {
// gap /= 2;
// for (int i = j; i < n - gap; i += gap)
// { //一组一组走
// int end = i;
// int tmp = a[end + gap];
// while (end >= 0)
// {
// if (tmp < a[end])
// {
// a[end + gap] = a[end];
// end -= gap;
// }
// else
// {
// break;
// }
// }
// a[end + gap] = tmp;
// }
// }
//}
/*希尔排序*/
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
/*
* gap > 1 —— 预排序
* gap == 1 —— 直接插入排序
*/
//gap /= 2;
gap = gap / 3 + 1; //保证最后的gap值为1,为直接插入排序
for (int i = 0; i < n - gap; i++)
{ //一位一位走
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
PrintArray(a, n);
}
}
/*传统选择排序*/
void SelectedSort(int* a, int n)
{
for (int i = 0; i < n - 1; ++i)
{
int k = i;
for (int j = i + 1; j < n; ++j)
{
if (a[j] < a[k]) k = j;
}
if (a[k] != a[i])
{
swap(&a[k], &a[i]);
}
}
}
/*简单选择排序*/
void SelectSort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int mini = begin;
int maxi = begin;
for (int i = begin + 1; i <= end; ++i)
{
if (a[i] < a[mini])
mini = i;
if (a[i] > a[maxi])
maxi = i;
}
swap(&a[begin], &a[mini]);
if (maxi == begin) //若是最大值和begin重合了,则重置一下交换后的最大值
maxi = mini;
swap(&a[end], &a[maxi]);
begin++;
end--;
}
}
/*向下调整算法*/
void Adjust_Down(int* a, int n, int parent)
{
int child = parent * 2 + 1; //默认左孩子来得大
while (child < n)
{ //判断是否存在右孩子,防止越界访问
if (child + 1 < n && a[child + 1] > a[child])
{
++child; //若右孩子来的大,则转化为右孩子
}
if (a[child] > a[parent])
{
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
/*堆排序*/
void HeapSort(int* a, int n)
{
//建立大根堆(倒数第一个非叶子结点)
for (int i = ((n - 1) - 1) / 2; i >= 0; --i)
{
Adjust_Down(a, n, i);
}
int end = n - 1;
while (end > 0)
{
swap(&a[0], &a[end]); //首先交换堆顶结点和堆底末梢结点
Adjust_Down(a, end, 0); //一一向前调整
end--;
}
}
/*冒泡排序*/
void BubbleSort(int* a, int n)
{
//[0,n - 1)
for (int i = 0; i < n - 1; ++i)
{
int changed = 0;
for (int j = 0; j < n - 1 - i; ++j)
{
if (a[j] > a[j + 1])
{
swap(&a[j], &a[j + 1]);
changed = 1;
}
}
if (changed == 0)
break;
//PrintArray(a, n);
}
//[1,n)
//for (int i = 1; i < n; ++i)
//{
// for (int j = 0; j < n - i; ++j)
// {
// if (a[j] > a[j + 1])
// swap(&a[j], &a[j + 1]);
// }
//}
}
/*三数取中*/
int GetMid(int* a, int left, int right)
{
/*
* 不是取中间的那个值,而是取三个数中不是最大也不是最小的那个
* --->进来可能是一个随机或有序序列,保证key最大或者最小就行
*/
int mid = (left + right) >> 1;
//int mid = left + rand() % (right - left);
if (a[mid] > a[left])
{
if (a[mid] < a[right])
{ //left mid right
return mid;
}
//另外两种mid一定是最大的,比较left和right
else if (a[left] > a[right])
{ //right left mid
return left;
}
else
{ //left right mid
return right;
}
}
else //a[left] >= a[mid]
{
if (a[mid] > a[right])
{ //right mid left
return mid;
}
//另外两种mid一定是最小的,比较left和right
else if (a[left] < a[right])
{ //mid left right
return left;
}
else
{ //mid right left
return right;
}
}
}
/*快速排序 —— hoare版本(左右指针法)*/
int PartSort1(int* a, int begin, int end)
{
/*
* 找小 —— 是找真的比我小的
* 找大 —— 是找真的比我大的
* --->相等均要略过
*
* 还要防止越界【left < right】
*/
//三数取中
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]); //交换begin上的值和找出的中间值
int left = begin;
int right = end;
int keyi = begin; //以最左边作为对照值记录,右边先走
while (left < right)
{
//右边找比keyi所在位置小的值,若是 >= 则忽略(加上=防止死循环)
while (left < right && a[right] >= a[keyi])
{ //left < right —— 防止特殊情况越界
right--;
}
//左边找比keyi所在位置大的值,若是 <= 则忽略
while (left < right && a[left] <= a[keyi])
{
left++;
}
//都找到了,则交换
swap(&a[left], &a[right]);
}
//最后当left和right相遇的时候将相遇位置的值与keyi位置的值交换
swap(&a[left], &a[keyi]);
keyi = left; //因keyi位置的值被交换到相遇点,因此更新准备分化递归
return keyi;
}
/*快速排序 —— 挖坑法*/
int PartSort2(int* a, int begin, int end)
{
//三数取中
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int left = begin, right = end;
int hole = left; //坑位
int key = a[hole]; //记录坑位上的值
while (left < right)
{
//右边找小,放入坑位,然后更新坑位
while (left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
//左边找大,放入坑位,然后更新坑位
while (left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
return hole;
}
/*快速排序 —— 前后指针法*/
int PartSort3(int* a, int begin, int end)
{
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int prev = begin;
int cur = prev + 1;
int keyi = prev;
while (cur <= end)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
swap(&a[prev], &a[cur]);
}
cur++; //cur无论如何都要++,因此直接写在外面
}
//cur超出右边界后交换prev处的值和key
swap(&a[keyi], &a[prev]);
return prev;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
return; //最后递归下去区间不存在了,进行递归回调
//小区间优化
if ((end - begin + 1) < 15)
{
//在数据量少的时候改用直接插入排序
InsertSort(a + begin, end - begin + 1);
}
//int key = PartSort1(a, begin, end); //左右指针法
//int key = PartSort2(a, begin, end); //挖坑法
int key = PartSort3(a, begin, end); //前后指针法
//左右区间分化递归
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}
/*快速排序——三路划分法*/
void QuickSortThreeDivisioin(int* a, int begin, int end)
{
if (begin >= end)
return; //最后递归下去区间不存在了,进行递归回调
//小区间优化
if ((end - begin + 1) < 15)
{
//在数据量少的时候改用直接插入排序
InsertSort(a + begin, end - begin + 1);
}
else
{
//三数取中
int mid = GetMid(a, begin, end);
swap(&a[begin], &a[mid]);
int key = a[begin];
int left = begin;
int cur = left + 1;
int right = end;
while (cur <= right)
{
if (a[cur] < key)
{
swap(&a[left++], &a[cur++]);
}
else if (a[cur] > key)
{
swap(&a[cur], &a[right--]);
//此时cur不变化是因为从right换到中间的值可能还是比key大,为了在下一次继续进行比较
}
else
{
cur++;
}
}
//[begin, left - 1][left, right][right + 1, end]
QuickSortThreeDivisioin(a, begin, left - 1);
QuickSortThreeDivisioin(a, right + 1, end);
}
}
/*快速排序——非递归*/
void QuickSortNonR(int* a, int begin, int end)
{
ST st;
InitStack(&st);
//首先将整体区间入栈
PushStack(&st, begin);
PushStack(&st, end);
while (!StackEmpty(&st))
{
//出栈分别获取右左两个端点
int right = StackTop(&st);
PopStack(&st);
int left = StackTop(&st);
PopStack(&st);
//求解keyi的位置
int keyi = PartSort3(a, left, right);
//先入右
if (keyi + 1 < right)
{ //若是区间的值 > 1,则继续入栈
PushStack(&st, keyi + 1);
PushStack(&st, right);
}
//后入左
if (left < keyi - 1)
{ //若是区间的值 > 1,则继续入栈
PushStack(&st, left);
PushStack(&st, keyi - 1);
}
}
DestroyStack(&st);
}
void _MergeSort(int* a, int begin, int end, int* tmp)
{
//递归出口
if (begin >= end)
{
return;
}
int mid = (begin + end) >> 1;
/*
* [begin, mid][mid + 1, end]
* --->继续进行子区间归并,相当于后序遍历【左,右,根】
*/
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid + 1, end, tmp);
int i = begin; //i要从每次递归进来的begin开始放,可能是在右半区间
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
//若是还有区间存在数据,表示没有归并完全,直接放入tmp即可
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//最后将归并完后后的数据拷贝回原数组
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
/*归并排序*/
//时间复杂度:O(NlogN)
//空间复杂度:O(N)
void MergeSort(int* a, int n)
{
//开辟空间,存放归并后的数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("fail malloc");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp); //防止内存泄漏
tmp = NULL; //防止野指针
}
/*归并排序——非递归*/
void MergeSortNonR1(int* a, int n)
{
//开辟空间,存放归并后的数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("fail malloc");
exit(-1);
}
int rangeN = 1;
while (rangeN < n)
{
for (int i = 0; i < n; i += 2 * rangeN)
{
int begin1 = i, end1 = i + rangeN - 1;
int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;
printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
int j = i; //表示tmp每次都从上一次归并完放置后的地方开始
/*
* 处理越界的情况
*/
if (end1 >= n) {
break;
}
else if (begin2 >= n) {
break;
}
else if (end2 >= n) {
end2 = n - 1; //end2越界要修正一下,不可以break,因为最后需要求整个数组的长度
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
//若是还有区间存在数据,表示没有归并完全,直接放入tmp即可
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
//归并完一小组,拷贝一小组
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
// + i表示每次归并的组在发生变化 //因为end是最后落的位置,i是初始化位置,不会改变
}
rangeN *= 2;
}
free(tmp); //防止内存泄漏
tmp = NULL; //防止野指针
}
void MergeSortNonR2(int* a, int n)
{
//开辟空间,存放归并后的数组
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("fail malloc");
exit(-1);
}
int rangeN = 1;
while (rangeN < n)
{
for (int i = 0; i < n; i += 2 * rangeN)
{
int begin1 = i, end1 = i + rangeN - 1;
int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;
int j = i; //表示tmp每次都从上一次归并完放置后的地方开始
printf("[%d,%d][%d,%d]\n", begin1, end1, begin2, end2);
/*
* 处理越界的情况
*/
if (end1 >= n) {
end1 = n - 1;
begin2 = n; //begin2要比end2来的大,才不构成区间
end2 = n - 1;
}
else if (begin2 >= n) {
begin2 = n; //begin2要比end2来的大,才不构成区间
end2 = n - 1;
}
else if (end2 >= n) {
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
//若是还有区间存在数据,表示没有归并完全,直接放入tmp即可
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
//整组中的所有小组都归并完了,一起拷贝回去
memcpy(a, tmp, sizeof(int) * n);
rangeN *= 2;
}
free(tmp); //防止内存泄漏
tmp = NULL; //防止野指针
}
/*计数排序*/
void CountSort(int* a, int n)
{
//1.找出数组中的最大值和最小值,然后开辟统计数组
int min = a[0];
int max = a[0];
for (int i = 0; i < n; ++i)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
int range = max - min + 1; //数据范围
int* CountArray = (int*)malloc(sizeof(int) * range);
memset(CountArray, 0, sizeof(int) * range); //初始化数组均为0
//2.统计数组中每一个数出现的个数,映射到CountArray数组中
for (int i = 0; i < n; ++i)
{
CountArray[a[i] - min]++;
//a[i] - min 表示找出相对位置
}
//3.将统计数组中的数写回原数组中,进行排序
int index = 0;
for (int j = 0; j < range; ++j)
{
//根据统计数组去找出每个数要写回几次
while (CountArray[j]--)
{
a[index++] = j + min;
//每次循环中的j不会发生变化,加上最小值可以找回原来的数字
}
}
}
//获取当前数字的待判位数【个、十、百】
//value: 789
// k: 0
int GetKey(int value, int k)
{
int key = 0;
while(k >= 0)
{
key = value % 10;
value /= 10;
k--;
}
return key;
}
//分发数据
void Distribute(int* a, int n, int k)
{
for (int i = 0; i < n; ++i)
{
int key = GetKey(a[i], k);
qu[key].push(a[i]);
}
}
//回收数据
void Collect(int* a)
{
int index = 0;
for (int i = 0; i < RADIX; ++i)
{
while (!qu[i].empty())
{
a[index++] = qu[i].front();
qu[i].pop();
}
}
}
//求解数组中的最大值
int GetMax(int* a, int n)
{
int max = a[0];
for (int i = 0; i < n; ++i)
{
if (a[i] > max)
max = a[i];
}
return max;
}
//求解最大值的位数
int GetDigit(int num)
{
//num : 10000
int count = 0;
while (num > 0)
{
count++;
num /= 10;
}
return count;
}
/*基数排序*/
void RadixSort(int* a, int n)
{
//首先求出数组中的最大值
int max = GetMax(a, n);
//求出最大值的位数
int k = GetDigit(max);
//进行K次的数据分发和回收
for (int i = 0; i < k; ++i)
{
//分发数据
Distribute(a, n, i);
//回收数据
Collect(a);
}
}
/*桶排序*/
void BucketSort(int* a, int n)
{
int bucket[5][5]; // 分配五个桶。
int bucketsize[5]; // 每个桶中元素个数的计数器。
// 初始化桶和桶计数器。
memset(bucket, 0, sizeof(bucket));
memset(bucketsize, 0, sizeof(bucketsize));
// 把数组a的数据按照范围放入对应桶中
for (int i = 0; i < n; ++i)
{
bucket[a[i] / 10][bucketsize[a[i] / 10]++] = a[i];
}
// 分别对每个桶中的数据进行排序
for (int i = 0; i < 5; ++i)
{
QuickSort(bucket[i], 0, bucketsize[i] - 1);
}
// 将把每个桶中的数据依次放回数组a中
int index = 0;
for (int i = 0; i < 5; ++i)
{
for (int j = 0; j < bucketsize[i]; ++j)
{
a[index++] = bucket[i][j];
}
}
}
//文件归并逻辑
void _MergeSortFile(const char* file1, const char* file2, const char* mfile)
{
FILE* fout1 = fopen(file1, "r");
if (!fout1)
{
perror("fopen fail");
exit(-1);
}
FILE* fout2 = fopen(file2, "r");
if (!fout2)
{
perror("fopen fail");
exit(-1);
}
FILE* fin = fopen(mfile, "w");
if (!fin)
{
perror("fopen fail");
exit(-1);
}
int num1, num2;
//返回值拿到循环外来接受
int ret1 = fscanf(fout1, "%d\n", &num1);
int ret2 = fscanf(fout2, "%d\n", &num2);
while (ret1 != EOF && ret2 != EOF)
{
if (num1 < num2)
{
fprintf(fin, "%d\n", num1);
ret1 = fscanf(fout1, "%d\n", &num1);
}
else
{
fprintf(fin, "%d\n", num2);
ret2 = fscanf(fout2, "%d\n", &num2);
}
}
while (ret1 != EOF)
{
fprintf(fin, "%d\n", num1);
ret1 = fscanf(fout1, "%d\n", &num1);
}
while (ret2 != EOF)
{
fprintf(fin, "%d\n", num2);
ret2 = fscanf(fout2, "%d\n", &num2);
}
fclose(fout1);
fclose(fout2);
fclose(fin);
}
/*文件外排序*/
void MergeSortFile(const char* file)
{
srand((unsigned int)time(NULL));
FILE* fout = fopen(file, "r");
if (!fout)
{
perror("fopen fail");
exit(-1);
}
//先写100个随机数进文件
//for (int i = 0; i < 100; ++i)
//{
// int num = rand() % 100;
// fprintf(fout, "%d\n", num);
//}
int num = 0;
int n = 10;
int i = 0;
int b[10];
char subfile[20];
int filei = 1;
//1.读取大文件,然后将其平均分成N份,加载到内存中后对每份进行排序,然后再写回小文件
memset(b, 0, sizeof(int) * n);
while (fscanf(fout, "%d\n", &num) != EOF)
{
if (i < n - 1)
{
b[i++] = num; //首先读9个数据到数组中
}
else
{
b[i] = num; //再将第十个输入放入数组
QuickSort(b, 0, n - 1); //对其进行排序
sprintf(subfile, "%d", filei++);
FILE* fin = fopen(subfile, "w");
if (!fin)
{
perror("fopen fail");
exit(-1);
}
//再进本轮排好序的10个数以单个小文件的形式写到工程文件下
for (int j = 0; j < n; ++j)
{
fprintf(fin, "%d\n", b[j]);
}
fclose(fin);
i = 0; //i重新置0,方便下一次的读取
memset(b, 0, sizeof(int) * n);
}
}
//利用互相归并到文件,实现整体有序
char file1[100] = "1";
char file2[100] = "2";
char mfile[100] = "12";
for (int i = 2; i <= n; ++i)
{
_MergeSortFile(file1, file2, mfile);
//迭代
strcpy(file1, mfile);
sprintf(file2, "%d", i + 1);
sprintf(mfile, "%s%d", mfile, i + 1);
}
}
test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include "sort.h"
void TestInsertSort()
{
int a[] = { 3,5,9,1,7,4,2,10,6,8 };
int sz = sizeof(a) / sizeof(int);
InsertSort(a, sz);
PrintArray(a, sz);
}
void TestShellSort()
{
int a[] = { 9,5,3,1,7,4,2,10,6,8 };
int sz = sizeof(a) / sizeof(int);
PrintArray(a, sz);
ShellSort(a, sz);
PrintArray(a, sz);
}
void TestSelectSort()
{
int a[] = { 3,5,9,1,7,4,2,10,6,8 };
int a2[] = { 10,5,9,1,7,4,2,3,6,8 };
int sz = sizeof(a) / sizeof(int);
int sz2 = sizeof(a2) / sizeof(int);
//SelectedSort(a, sz);
SelectSort(a, sz);
PrintArray(a, sz);
SelectSort(a2, sz2);
PrintArray(a2, sz2);
}
void TestHeapSort()
{
int a[] = { 3,5,9,1,7,4,2,10,6,8 };
int sz = sizeof(a) / sizeof(int);
HeapSort(a, sz);
PrintArray(a, sz);
}
void TestBubbleSort()
{
int a[] = { 3,5,9,1,7,4,2,10,6,8 };
int sz = sizeof(a) / sizeof(int);
BubbleSort(a, sz);
PrintArray(a, sz);
}
void TestQuickSort()
{
//int a[] = { 6,1,2,7,9,3,4,5,10,8 };
//int a[] = { 6,1,2,7,9,6,3,6,4,5,6,10,8,6 };
int a[] = { 2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2 };
//int a[] = { 0 };
int sz = sizeof(a) / sizeof(int);
QuickSort(a, 0, sz - 1); //递归
//QuickSortNonR(a, 0, sz - 1); //非递归
//QuickSortThreeDivisioin(a, 0, sz - 1);
PrintArray(a, sz);
}
void TestMergeSort()
{
int a[] = { 3,5,9,1,7,4,2,10,6,8 };
//int a[] = { 10,6,7,1,3,9,4,2 };
int sz = sizeof(a) / sizeof(int);
//MergeSort(a, sz);
//MergeSortNonR1(a, sz);
MergeSortNonR2(a, sz);
PrintArray(a, sz);
}
void TestCountSort()
{
//int a[] = {3,2,5,0,3,2,0,3};
int a[] = {1000, 1001, 1003, 1001};
int sz = sizeof(a) / sizeof(int);
PrintArray(a, sz);
CountSort(a, sz);
PrintArray(a, sz);
}
void TestBucketSort()
{
int a[] = { 32,16,21,1,39,9,7,44,25,48 };
int sz = sizeof(a) / sizeof(int);
PrintArray(a, sz);
BucketSort(a, sz);
PrintArray(a, sz);
}
void TestRadixSort()
{
//int a[] = { 789,159,357,14,2,590,447,123,1};
//int a[] = { 789,159,357,14,2,590,447,123,1,4444};
int a[] = { 78999,159,357,14,2,590,447,123,1,4444};
int sz = sizeof(a) / sizeof(int);
RadixSort(a, sz);
PrintArray(a, sz);
}
// 测试排序的性能对比
void TestOP()
{
srand(time(0));
const int N = 10000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
int* a6 = (int*)malloc(sizeof(int) * N);
int* a7 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; ++i)
{
a1[i] = rand();
//a1[i] = i;
a2[i] = a1[i];
a3[i] = a1[i];
a4[i] = a1[i];
a5[i] = a1[i];
a6[i] = a1[i];
a7[i] = a1[i];
}
//int j = 0; //统计放入了几个随机值
//for (int i = 0; i < N; ++i)
//{
// int x = rand();
// if (x % 7 == 0 && x % 3 == 0)
// {
// a1[i] = x; //在随机的位置放入这个随机数
// ++j; //插入多少随机数的累加
// }
// else
// {
// a1[i] = i; //表示整体是有序的
// }
// a2[i] = a1[i];
// a3[i] = a1[i];
// a4[i] = a1[i];
// a5[i] = a1[i];
// a6[i] = a1[i];
// a7[i] = a1[i];
//}
//printf("%d\n", j);
int begin1 = clock();
//InsertSort(a1, N); //直接插入排序
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N); //希尔排序
int end2 = clock();
int begin3 = clock();
//SelectSort(a3, N); //选择排序
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N); //堆排序
int end4 = clock();
int begin5 = clock();
//BubbleSort(a5, N); //冒泡排序
int end5 = clock();
int begin6 = clock();
QuickSort(a5, 0, N - 1); //快速排序
int end6 = clock();
int begin7 = clock();
//(a7, N); //归并排序
int end7 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("SelectSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("BubbleSort:%d\n", end5 - begin5);
printf("QuickSort:%d\n", end6 - begin6);
//printf("MergeSort:%d\n", end7 - begin7);
free(a1);
free(a2);
free(a3);
free(a4);
free(a5);
free(a6);
}
int main(void)
{
//TestInsertSort();
//TestShellSort();
//TestSelectSort();
//TestHeapSort();
//TestBubbleSort();
//TestQuickSort();
//TestMergeSort();
//TestCountSort();
//TestBucketSort();
//TestRadixSort();
MergeSortFile("SortData.txt");
//TestOP();
return 0;
}
LeetCode实战演练
有关排序相关的OJ,LeetCode上的很多题目都可以穿插进去,但是比较有代表性的还是这一道,可以直接测试你的排序代码写的是否有问题
原题传送门
- 在本题中,O(NlogN)几个排序都是可以过的,但是快速排序过不了,这是因为前段时间这道题目多了一个测试用例,非常得极端,所以导致快速排序在选key时候选的就很极端
- 但是这个情况我们上面有分析到过了,那就是使用【三路划分法】,如果有忘记的小伙伴记得上去再看看哦
- 下面这本题的运行结果,代码的话我已经给大家了
超时通不过的几个O(N2)排序
整体通过率
⌚稳定性分析 + 各大排序算法性能测试
首先我们来聊聊排序的【稳定性】,然后再把我们上面所讲的排序总结一下
- 首先什么是排序的稳定性呢?来看看权威解释
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的【来源于百度百科】
- 然后我们通过图示来看看
- 为什么要说稳定性呢,因为接下去我们就要分析各大排序在执行的过程中是否稳定了
- 下面是我精心制作的总结图,一些原因及分析都注在旁边了,希望您可以看得懂
接下去我们对各大排序的算法性能做一个测试
不要问为什么少了一个,那就是桶排序,因为随着数据量的增大,无法确定桶的数量以及平均分配每个桶中的数据个数,所以桶排序只适合于小型数据的场合,它已退出本趴的聊天
- 我们主要来看的是两大场景,一个是数据有序,一个是数据无序(随机值)
首先我们来看看数据无序的场景
- 上下这两张的数据是随机产生的,数据量都是一样为【100000】,可以看到在排序众多随机值的场合下,三个O(N2)的排序算法【直插】【选择】【冒泡】的速度都是占下风,特别是对于冒泡排序而言,乱序简直是它的噩梦;四个O(NlogN)的排序【希尔】【堆排】【快排】【归并】差不多时间;计数排序是一匹黑马,很强大
- 下面是对于快速排序的遏制,我将三数取中去除之后面对海量的随机值,就会遇到很极端的key值,便使得快速排序退化成了O(N2)
接下去我们来看看数据有序的场景
- 可以看出,对于已然有序的数据进行排序时,大家都很快,但还有一个排序傻傻地在一个个进行比较然后置换,那么就是【选择排序】,上面也分析了它的最好、最坏和平均时间复杂度,均为O(N2)
- 这里要测试的还是对于快速排序来说有无三数取中,对于上图来说快速排序加了三数取中但是在下图中我又取消了【三数取中】,此时可以看到,对快排也是一个致命的影响,无论是在有序还是无序的场景下
看到上面的的测试中,计数排序总是那么能打,现在我们遏制一下它,增大这个range范围
- 可以看到,当这个range范围增大的时候,无论是有序还是无序的场合下,都跟不上性能了。所以无论是对于什么排序,无论再怎么有优势,只有设置一下固定的数据场景,就会出现劣势一面
- 看完上面的这些测试,相信你对我们上面所学习的排序有了一个更加深入的理解,其实还是很多数据的场景可以测试,这里就不一一展示了,代码也给到大家,若是有特定场景可以自己去测试一番,就可以知道这些排序算法性能的优劣了
✒总结与提炼
最后,我们来总结和回顾一下本文学习的所有内容
-
本文,我们对十大排序算法进行了一个总结和回顾,分别从它们的整体过程、算法思路、代码分析、复杂度分析这几块做了一个了解
-
[直接插入排序]:使用得比较广泛,虽属于O(N2)的排序算法,但是在数据接近有序时能体现出优势,需要掌握
-
[希尔排序]:看起来不起眼,但是性能不错,平均时间复杂度也能达到O(NlogN),至于O(N1.3)了解一下即可,主要还是记住它排序的这个过程
-
[选择排序]:如果能想得起其他排序算法,就不要用这个了,在各种场合测试下它都是最差劲的,无论如何都是在选数然后交换的过程
-
[堆排序]:性能不错,重点掌握的是【向下调整算法】以及如何建堆的过程,在数据量特大的情况下可以使用
-
[冒泡排序]:大学生最喜欢用排序算法,性能不高,只有在序列已然有序或者接近有序的情况下才能展现出优势
-
[快速排序]:综合性能最优,包含【左右指针法】【挖坑法】【前后指针法】【三路划分法】,学有余力都应掌握,重点在理解Hoare版本的思路。对于要参加校招的同学还要求掌握非递归的写法
-
[归并排序]:即使内排序也是排序,性能较高又可以达到稳定,常用于文件外排序。也有递归和非递归两种写法,最好是都要掌握
-
[计数排序]:唯一一个可能达到O(N)时间复杂度的排序算法,若是序列中没有很极端的数据出现,那用它还是不错的
-
[桶排序]:对于桶和桶中数据的分配在数据量增大时候很难分配,总体性能也不是很优,需要很强的代码控制能力
-
[基数排序]:属于桶排序的一种,校招不考,原理思路以及数据的划分过程可以了解一下,很是巧妙,不过平常用得也不是很广泛
-
最后还对所有排序的整体做了一个稳定性和性能方面的测试,也很好地帮助大家对排序算法更上一层,文章中图示均是使用电脑自带的画图完成的,如有需要可以私信我
完结撒花
<参考文献资料>
以下是我在写这篇文章时参考的资料和内容,尊重作者,附上链接
1、排序的概念详解—— 科普中国
2、快速排序(Quicksort)—— 百度百科
3、十大经典排序算法详解(三)-堆排序,计数排序,桶排序,基数排序
4、排序算法之 计数排序 及其时间复杂度和空间复杂度
5、基数排序(详细图解)
6、八大排序算法(C语言实现)
7、【数据结构从青铜到王者】第九篇:数据结构之排序
8、常见排序算法详解:插入,冒泡,希尔,选择,快速排序,归并,计数排序,堆排序(已完结)
9、【数据结构初阶】八大排序算法+时空复杂度
10、排序算法稳定性 —— 百度百科
最后非常感谢您对本文的阅读,如果觉得写的还可以,非常希望得到您的三连支持。如有疑问请于评论区留言或者私信我