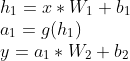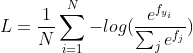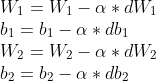基于MATLAB实现简单人工神经网络

资源下载地址：https://download.csdn.net/download/sheziqiong/85979688
资源下载地址：https://download.csdn.net/download/sheziqiong/85979688

1.MNIST 数据集简介

MNIST 是在机器学习领域中的一个经典问题。该问题解决的是把 28x28 像素的灰度手写数字图片识别为相应的数字，其中数字的范围从 0 到 9。

mnist_uint8.mat 包含了 MNIST 数据集的全部数据，其中：

train_x: 60000*784 矩阵，60000 个训练样本，每个训练样本像素值展开成了行向量。

train_y: 60000*10 矩阵，60000 个训练样本标签，每个样本标签中对应分类元素值为 1，其余为 0；

test_x: 10000*784 矩阵，10000 个测试样本，每个训练样本像素值展开成了行向量。

test_y: 10000*10 矩阵，10000 个测试样本标签，每个样本标签中对应分类元素值为 1，其余为 0；

2. 人工神经网络简介

2.1 网络结构

一个基本的人工神经网络结构主要由以下三部分构成：输入层(x)、一个或多个隐藏层(h)、输出层(y)。

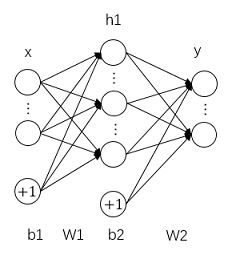
输入层：输入层用于输入特征向量，对于手写体图像，我们可以简单的将图像的所有像素灰度值排列成向量输入神经网络.

隐藏层：输入层和输出层之间的神经网络被称作隐藏层，每一层中包含多个神经元节点，每个节点都有自己的激励值，每个节点的激励值由上层节点激励计算得到，由此构成网状连接的结构，计算得到的激励还需要经过一个非线性函数。

非线性激活函数：用于将线性的节点连接过程转换成非线性，常用的非线性激活函数有：sigmoid 函数、tanh 函数、ReLU 函数等。

输出层：输出神经网络的预测结果，对于手写体识别问题，有 0-9 十个分类，因此输出层有十个输出，输出节点值越大，表示预测结果越可能属于它对应的分类。

2.2 工作过程

神经网络的工作过程主要分为训练和测试，训练是每次将若干个训练集样本输入到网络中，进行前向传播、后向传播和梯度下降，对网络中随机初始化的权重进行优化。网路训练是一个循环的过程，对权重和偏置不断的梯度下降使损失函数越来越小，网络输出的结果接近真实标签，具体的训练流程如下：

1. 随机初始化权重值
2. 训练样本输入前向传播
3. 计算损失函数
4. 后向传播
5. 梯度下降
6. 重复 2-5

网络的测试则是使用测试集对已经训练好的网络前向传播进行测试，验证网络的性能。

2.3 前向传播

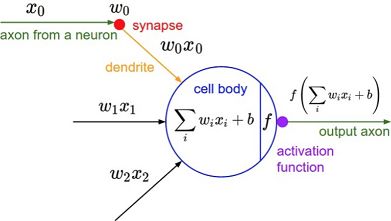
在神经网络层之间具体的连接计算方式为：后一层每个节点的激励值都由上一层所有节点的激励加权求和，然后通过非线性激活函数。单个节点的连接计算如下图所示：

每一层所有神经元的加权求和的过程可以通过权重矩阵 W 与节点向量 x 相乘并加上偏置 b 表示。有一层隐藏层的人工神经网络可以由下面的数学形式表示：

其中 g( )表示非线性激活函数，这种不断由前一层输入得到后一层输出的计算方式称为前向传播。

2.4 损失函数

损失函数用来计算输出结果和真实值标签之间的差距，并用来指导权重和偏置的更新。对于多分类问题，一种常用的损失函数为 softmax 函数和交叉熵计算。

softmax 函数将网络的输出结果看作未归一化的对数概率，进行指数归一化。在一个数组 V 中，Vk 表示 V 中的第 k 个元素，那么这个元素的 Softmax 值就是：

由 softmax 值可以计算交叉熵作为损失，对于输入网络的 N 个样本，第 i 个样本的交叉熵定义为：

其中，log 中就是第 i 个样本中真实分类对应的 softmax 值。

最后，由于每次训练时输入了若干个训练样本，每个样本都会得到一个损失，对单次训练中所有样本得到的损失进行平均，我们能够得到每次训练的损失值：

2.5 后向传播

后向传播的过程正好和前向传播流程相反，后向传播用于计算网络中所有参数对于损失函数值的偏导。应用求导链式法则，对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。

具体的后向传播计算可以通过画出计算图的方法来辅助求解。

首先以最简单的算式为例。其中：设 y 矩阵维度为 N x a2，x 矩阵维度为 N x a1，W 矩阵维度为 a1 x a2，b 向量长度为 a2。以运算符乘（mul）和加（plus）为节点，可以构建有向的运算图：

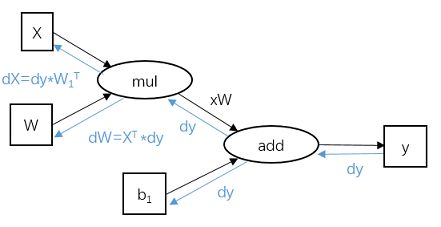
在后向传播过程中，可以看到过程和前向传播相反，并且从 y 开始从后向前传播。dy 是由后层网络传播得到的损失函数对 y 的偏导，由于损失 L 为一个标量，dy 和 y 同维。对于加法运算符，相当于路由，将 dy 梯度传给了参与加和的元素；对于乘法运算符，根据求导法则，每一个矩阵的雅可比矩阵可以由另一个参与相乘的矩阵与 dy 相乘得到。具体的形式可以展开矩阵元素验证。

将每一个运算的计算图连接起来最后能够得到完整的计算图，还是以一层隐藏层的人工神经网络为例，以计算图表示其后向传播过程为：

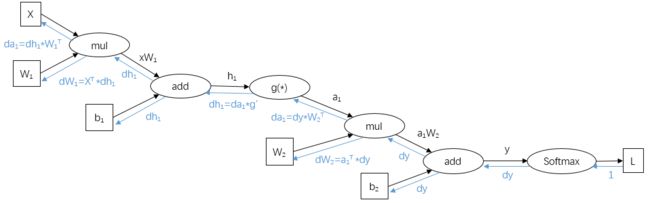
其中，softmax 的后向传播过程也可以通过计算图辅助的方式推导得到。

2.6 梯度下降

梯度给出了网络优化的方向，向负梯度方向不断更新参数可以使网络的输出向极小值靠近。限制于内存，我们不会每个将整个训练集输入网络进行训练，而是每次随机从训练集中选择部分样本组成小批量进行训练。对于每一个参数，梯度下降的表达式为：

θ 待更新的参数，α 是学习率，是 m 个样本批量单步训练计算得到的损失函数 L 对参数的梯度，由后向传播计算的偏导得到。

对于一层隐藏层的人工神经网络中权重和偏置的梯度下降，可以表示为：

α 学习率的大小在训练时起到了关键的作用。如果学习率太小，参数的梯度下降很小，训练很慢，损失函数的错误率会一直维持很高的水平。如果学习率太大，梯度下降会跳过极小值，同样会导致训练缓慢，甚至训练发散。一般需要实验确定学习率的大小。

3. 手写体识别程序

3.1 read_mnist.m

读取数据集函数

程序实现：

无

3.2 softmax_backward.m

softmax 分类损失后向传播函数

程序实现

• softmax 分类损失后向传播

3.3 softmax_forward.m

softmax 分类损失前向传播函数

程序实现：

• softmax 分类损失前向传播

3.4 test.m

网络模型测试函数

程序实现：

• 网络构建，测试错误率计算

3.5 train.m

完整训练过程实现函数

程序实现：

• 参数设置（可以尝试自己修改）
• 随机小批量训练集读取
• 计算错误率
• 记录下使用的隐藏层个数和学习率

3.6 train_step.m

一层隐藏层人工神经网络单步训练的实现

程序实现：

• 人工神经网络的的前向传播
• 人工神经网络的的后向传播
• 梯度下降
  资源下载地址：https://download.csdn.net/download/sheziqiong/85979688
  资源下载地址：https://download.csdn.net/download/sheziqiong/85979688