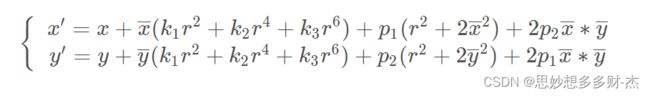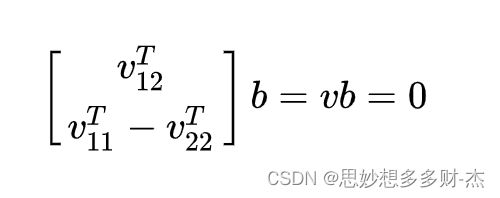计算机视觉（相机标定；内参；外参；畸变系数）

目录

一、预备知识

1、坐标系变换过程（相机成像过程）

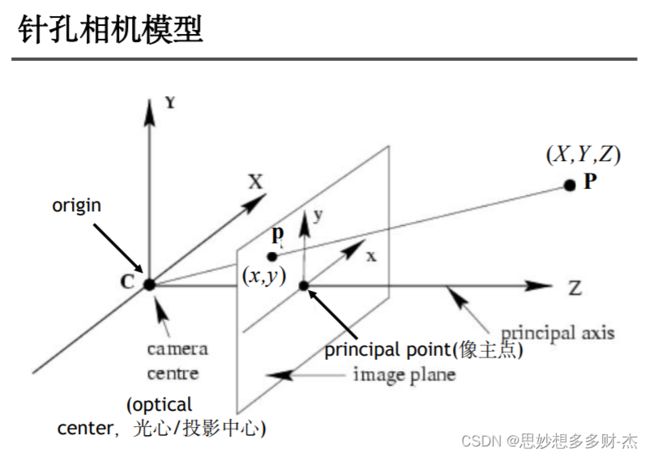
（1）相机坐标系转换为图像坐标系（透视投影变换遵循的是针孔成像原理）

（2）齐次坐标的引入原因：（为什么引入齐次坐标？？？）

2、内参与外参矩阵的构成

3、畸变参数

二、相机标定

1、张正友标定法（光学标定）及其求解思路

 2、求解内参矩阵与外参矩阵的思路：

（1）计算内参与外参矩阵的乘积M

（2）求解内参矩阵A

（3）求解外参矩阵(R1 R2 T)

三、参数优化

1、L-M算法

2、相机标定步骤

四、相关代码及其实验结果

1、相同角度的相机标定

（1）正面

内参矩阵：

畸变参数

旋转矩阵

 平移矢量

 反投影误差

 （2）侧面

内参矩阵

畸变参数

 旋转矩阵

 平移向量

反投影误差

 2、不同角度的相机标定

内参矩阵

畸变参数

旋转矩阵

平移矩阵

反投影误差

6、总结

---

一、预备知识

1、坐标系变换过程（相机成像过程）

相机成像过程涉及到四个坐标系的变换，变换关系如下：

（U,V,W）是世界坐标系，经过刚体变换（如：旋转、平移）后变为了相机坐标系，再次经过透视投影转变为了图像坐标系，最后经仿射变换转换为了像素坐标系（u,v）。转换关系如下(Z是尺度因子)：

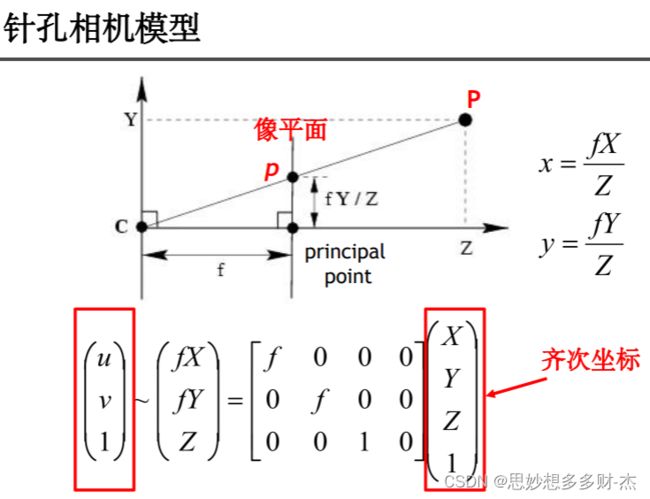
（1）相机坐标系转换为图像坐标系（透视投影变换遵循的是针孔成像原理）

（2）齐次坐标的引入原因：（为什么引入齐次坐标？？？）

总结如下：

a. 升维---把图像的变换表示为矩阵相乘的形式，以进行统一计算

图像的变换大多可以使用矩阵乘法来表示变换前后像素的映射关系，但是平移关系却只能使用矩阵加法表示，无法使用矩阵乘法表示。在表示图像变换时（如平移、旋转、缩放），矩阵涉及到乘法与加法，会使计算增加。

所以通过升维的方式来统一矩阵的形式，进而减少计算量。

b. 升维---把无穷远的坐标表示为可运用计算的形式

例子：如果笛卡尔坐标系下的点（3,4）移动到无穷远处，此时的坐标为（oo，oo）,使用齐次坐标就可以表示为（3,4,0）。

发现：使用齐次坐标，可以表示平行线在透视空间的无穷远处交于一点。在欧氏空间，这变得没有意义，所以欧式坐标不能表示。

齐次坐标转为欧式空间（3,4,5）=> (3/5,4/5) ---（6,8,10）=> (3/5,4/5)---（24,32,40）=> (3/5,4/5)

由此可以发现：齐次坐标具有规模不变性

2、内参与外参矩阵的构成

内参矩阵：只与相机本身有关，取决于相机的内部参数。

外参矩阵：相机拍摄图片不同，相应的参数会发生变化，即随着世界坐标系与相机坐标系的相对位置而变。

在相机标定求参数中，共有11个参数变量。其中，相机的内部参数有5个：焦距，像主点坐标，畸变参数；相机的外部参数有6个：旋转，平移。

内参矩阵表示为

 其中， f为像距，dX、dY分别表示X、Y方向上的一个像素在相机感光板上的物理长度，即一个像素在感光板上是多少毫米，u0，v0分别表示相机感光板中心在像素坐标系下的坐标，θ表示感光板的横边和纵边之间的角度（  90°表示无误差）。

外参矩阵表示为

  其中，R表示旋转矩阵，  T表示平移矢量。

3、畸变参数

畸变主要分为径向畸变和切向畸变。

径向畸变：沿着透镜半径方向分布的畸变；

产生原因：是由透镜质量引起的，光线在远离透镜中心的地方比靠近中心的地方更加弯曲。

径向畸变主要包括桶形畸变和枕形畸变两种。

切向畸变：切向畸变是由于透镜本身与相机传感器平面（像平面）或图像平面不平行而产生的。

 切向畸变主要发生在相机传感器和镜头不平行的情况下；因为有夹角，所以光透过镜头传到图像传感器上时，成像位置发生了变化。

畸变模型：

 径向畸变模型：

 切向畸变模型：

 径向畸变+切向畸变模型：

 畸变模型中（x',y'）为畸变后的归一化图像坐标，（x,y）为理想的无畸变的归一化的图像坐标。

 r为图像像素点到图像中心点的距离，即  。

 其中，k1、k2、k3是径向畸变参数；p1、p2切向畸变参数。

在无畸变的标定中，假设内参矩阵为 K，那么经过畸变之后会在矩阵中增加一个畸变参数。

——发生径向畸变之后——

二、相机标定

同步标定内部参数和外部参数，一般包括两种策略:

a. 光学标定: 利用已知的几何信息(如定长棋盘格)实现参数求解；

b. 自标定: 在静态场景中利用 structure from motion估算参数。

通过空间中已知坐标的(特征)点 (Xi,Yi,Zi)，以及它们在图像中的对应坐标 (ui,vi)，直接估算 11 个待求解的内部和外部参数。

1、张正友标定法（光学标定）及其求解思路

 参考：张正友相机标定法

张正友标定法利用棋盘格标定板图像，利用相应图像检测算法得到每个角点的像素坐标 （u,v）。

张正友标定法将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标W=0 ，由于标定板的世界坐标系是人为事先定义好的，标定板上每一个格子的大小是已知的，我们可以计算得到每一个角点在世界坐标系下的物理坐标(U,V,W=0)。

我们将利用这些信息：每一个角点的像素坐标(u,v) ，每一个角点在世界坐标系下的物理坐标(U,V,W=0)，来进行相机的标定，获得相机的内外参矩阵、畸变参数。

 2、求解内参矩阵与外参矩阵的思路：

将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标 W=0，因此，原单点无畸变的成像模型可以化为下式。其中，(R1 R2 T)为旋转矩阵R的前两列。

1. 计算内参与外参矩阵的乘积M--> 2. 求解内参矩阵A--> 3. 求解外参矩阵(R1 R2 T)

（1）计算内参与外参矩阵的乘积M

 其中，，M矩阵是齐次矩阵，有8个未知元素，每一个标定板上的角点，将提供两个约束方程。一张图片上只需4个角点即可求出矩阵M，一张图片上的角点多于4个时，可以使用最小二乘法求解最佳M。

（2）求解内参矩阵A

利用M1=A(R1,R2,T)求解内擦矩阵A。

 R1,R2作为旋转矩阵的两列，具有单位正交性，满足以下公式：

。

由，知

，

。

记，则

 其中，B为对称阵。

可记为，其中。

    

每张标定板图片可以提供一个vb=0的约束关系，该约束关系含有两个约束方程。但是，向量b有6个未知元素。取3张标定板照片即可求解向量b 。当标定板图片数大于3时，用最小二乘法拟合最佳的向量 b，并得到矩阵B ；进而求出内参矩阵A。

 

（3）求解外参矩阵(R1 R2 T)

对于不同的图片，标定板和相机的位置关系已经改变，此时每一张图片对应的外参矩阵都是不同的。

由 知外参矩阵可表示为：

 

即可求出每一张图片的外参矩阵。

完整的外参矩阵中旋转矩阵R有三列，其中通过计算R3=R1×R2，即可得到完整的外参矩阵。

三、参数优化

我们的总逻辑是，在进行内参矩阵和外参矩阵的求解的时候，我们假设不存在畸变；在进行畸变系数的求解的时候，假设求得的内参矩阵和外参矩阵是无误差的。最后，我们再通过L-M算法对于参数进行迭代优化。（张正友相机标定法仅考虑了畸变模型中影响较大的径向畸变）

1、L-M算法

L-M方法全称Levenberg-Marquardt方法，是非线性回归中回归参数最小二乘估计的一种估计方法。这种方法是把最速下降法和线性化方法(泰勒级数)加以综合的一种方法。因为最速下降法适用于迭代的开始阶段参数估计值远离最优值的情况，而线性化方法，即高斯牛顿法适用于迭代的后期，参数估计值接近最优值的范围内。两种方法结合起来可以较快地找到最优值  。

LM算法的迭代式：

由上式知：L-M算法是高斯牛顿法与梯度下降法的结合：当u很小时，矩阵J接近矩阵G，其相当于高斯-牛顿法，此时迭代收敛速度快，当u很大时，其相当于梯度下降法，此时迭代收敛速度慢。因此LM算法即具有高斯-牛顿法收敛速度快、不容易陷入局部极值的优点，也具有梯度下降法稳定逼近最优解的特点。

在LM算法的迭代过程中，需要根据实际情况改变u的大小来调整步长：

(1) 如果当前轮迭代的目标函数值大于上轮迭代的目标函数值，即，说明当前逼近方向出现偏差，导致跳过了最优点，需要通过增大u值来减小步长。

(2) 如果当前轮迭代的目标函数值小于上轮迭代的目标函数值，即，说明当前步长合适，可以通过减小u值来增大步长，加快收敛速度。

2、相机标定步骤

1. 打印一张棋盘格A4纸张（黑白间距已知），并贴在一个平板上；

2. 针对棋盘格拍摄若干张图片；

3. 在图片中检测特征点（Harris角点）；

4. 根据角点位置信息及图像中的坐标，求解内参矩阵与外参矩阵的积M ;

5. 利用B矩阵计算出5个内部参数得内部矩阵A，以及 6个外部参数 ;

6. 求解畸变参数；

7. 设计优化目标并实现参数的优化。

四、相关代码及其实验结果

引用代码：张正友相机标定法

import os
import numpy as np
import cv2
import glob


def calib(inter_corner_shape, size_per_grid, img_dir, img_type):
    # criteria: only for subpix calibration, which is not used here.
    # criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
    w, h = inter_corner_shape
    # cp_int: corner point in int form, save the coordinate of corner points in world space in 'int' form
    # like (0,0,0), (1,0,0), (2,0,0) ....,(10,7,0).
    cp_int = np.zeros((w * h, 3), np.float32) #返回来一个给定形状和类型的用0填充的数组  54行3列
    cp_int[:, :2] = np.mgrid[0:w, 0:h].T.reshape(-1, 2) #  三维网格坐标划分  行2列

    # cp_world: corner point in world space, save the coordinate of corner points in world space.
    cp_world = cp_int * size_per_grid

    obj_points = []  # the points in world space
    img_points = []  # the points in image space (relevant to obj_points)
    images = glob.glob(img_dir + os.sep + '**.' + img_type)
    for fname in images:
        img = cv2.imread(fname)
        gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        # find the corners, cp_img: corner points in pixel space.
        ret, cp_img = cv2.findChessboardCorners(gray_img, (w, h), None)
        # if ret is True, save.
        if ret == True:
            # cv2.cornerSubPix(gray_img,cp_img,(11,11),(-1,-1),criteria)
            obj_points.append(cp_world)
            img_points.append(cp_img)
            # view the corners
            cv2.drawChessboardCorners(img, (w, h), cp_img, ret)
            cv2.namedWindow('FoundCorners', cv2.WINDOW_NORMAL)
            cv2.resizeWindow("FoundCorners", 600, 600)  # 设置窗口大小
            cv2.imshow('FoundCorners', img)
            cv2.waitKey(1)
    cv2.destroyAllWindows()
    # calibrate the camera
    ret, mat_inter, coff_dis, v_rot, v_trans = cv2.calibrateCamera(obj_points, img_points, gray_img.shape[::-1], None,
                                                                   None)
#    print(("ret:"), ret)
    print(("internal matrix:\n"), mat_inter)
    # in the form of (k_1,k_2,p_1,p_2,k_3)
    print(("------------------------------------------------------------------"))
    print(("distortion cofficients:\n"), coff_dis) #畸变系数k1,k2,k3径向畸变系数, p1,p2是切向畸变系数。
    print(("------------------------------------------------------------------"))
    print(("rotation vectors:\n"), v_rot)
    print(("------------------------------------------------------------------"))
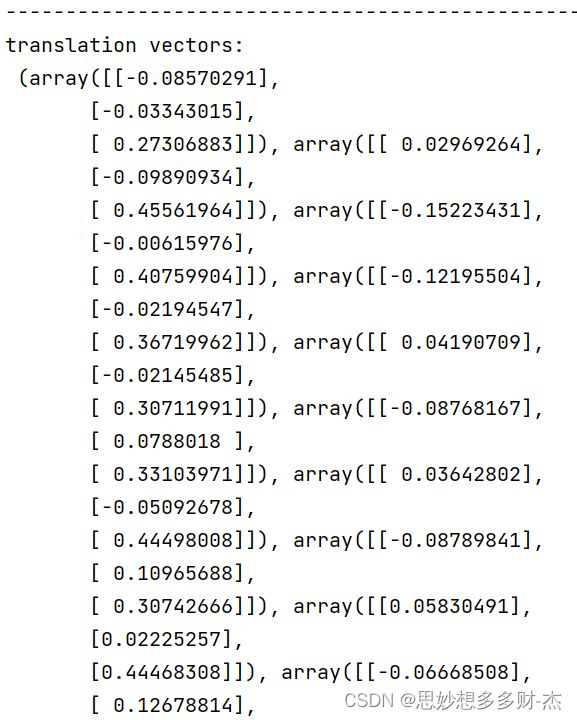
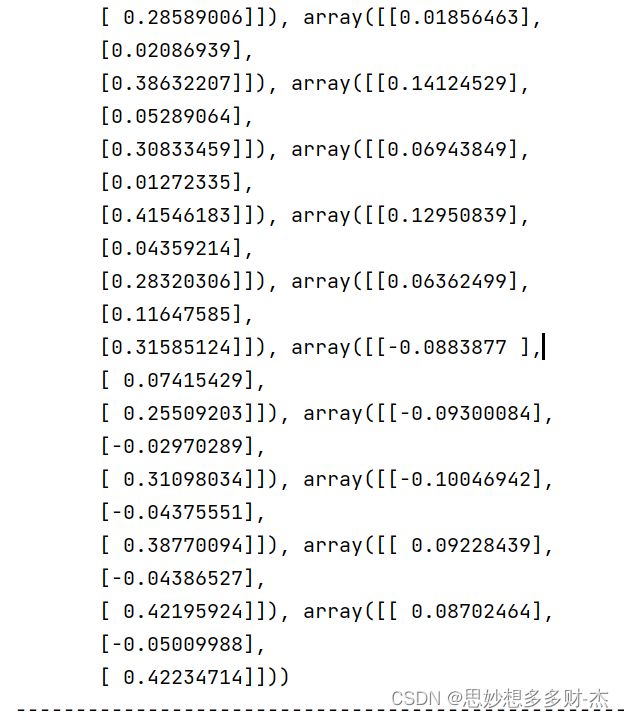
    print(("translation vectors:\n"), v_trans)
    print(("------------------------------------------------------------------"))
    # calculate the error of reproject
    # 反投影误差
    # 通过反投影误差，我们可以来评估结果的好坏。越接近0，说明结果越理想。
    # 通过之前计算的内参数矩阵、畸变系数、旋转矩阵和平移向量，使用cv2.projectPoints()计算三维点到二维图像的投影，
    # 然后计算反投影得到的点与图像上检测到的点的误差，最后计算一个对于所有标定图像的平均误差，这个值就是反投影误差
    total_error = 0
    for i in range(len(obj_points)):
        img_points_repro, _ = cv2.projectPoints(obj_points[i], v_rot[i], v_trans[i], mat_inter, coff_dis)
        error = cv2.norm(img_points[i], img_points_repro, cv2.NORM_L2) / len(img_points_repro)
        total_error += error
    print(("Average Error of Reproject: "), total_error / len(obj_points))
    return mat_inter, coff_dis

def dedistortion(inter_corner_shape, img_dir, img_type, save_dir, mat_inter, coff_dis):
    w, h = inter_corner_shape
    images = glob.glob(img_dir + os.sep + '**.' + img_type)
    for fname in images:
        img_name = fname.split(os.sep)[-1]
        img = cv2.imread(fname)
        newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mat_inter, coff_dis, (w, h), 0, (w, h))  # 自由比例参数
        dst = cv2.undistort(img, mat_inter, coff_dis, None, newcameramtx)
        # clip the image
        # x,y,w,h = roi
        # dst = dst[y:y+h, x:x+w]
        cv2.imwrite(save_dir + os.sep + img_name, dst)
    print('Dedistorted images have been saved to: %s successfully.' % save_dir)

if __name__ == '__main__':
    inter_corner_shape = (9, 6)
    size_per_grid = 0.026
    img_dir = ".\\pic\\photo5"
    img_type = "jpg"
    # calibrate the camera
    mat_inter, coff_dis = calib(inter_corner_shape, size_per_grid, img_dir, img_type)
    # dedistort and save the dedistortion result.
    save_dir = ".\\pic\\photo5-ch"
    if (not os.path.exists(save_dir)):
        os.makedirs(save_dir)
    dedistortion(inter_corner_shape, img_dir, img_type, save_dir, mat_inter, coff_dis)

1、相同角度的相机标定

（1）正面

 其中： 5张图片（1-5.jpg）10张图片（1-10.jpg）15张图片（1-15.jpg） 

内参矩阵：

5张图片

 10张图片

15张图片

畸变参数

5张图片

 10张图片

15张图片

旋转矩阵

5张图片

 10张图片

 15张图片

   

 平移矢量

5张图片

 10张图片

 15张图片

 反投影误差

5张图片

 10张图片

 15张图片

 （2）侧面

 其中： 5张图片（1-5.jpg）10张图片（1-10.jpg）15张图片（1-15.jpg）

内参矩阵

5张图片

 10张图片

15张图片

畸变参数

5张图片

 10张图片

15张图片

 旋转矩阵

5张图片

 10张图片

  15张图片

  

  平移向量

5张图片

10张图片

15张图片

   

 反投影误差

5张图片

 10张图片

 15张图片

 2、不同角度的相机标定

 其中： 5张图片（1-5.jpg）10张图片（1-10.jpg）15张图片（1-15.jpg） 20张图片(1-20.jpg)

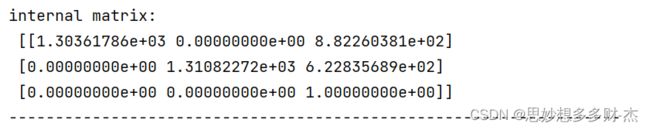
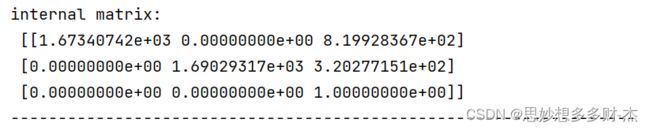
内参矩阵

5张图片

10张图片

15张图片

20张图片

畸变参数

5张图片

10张图片

15张图片

20张图片

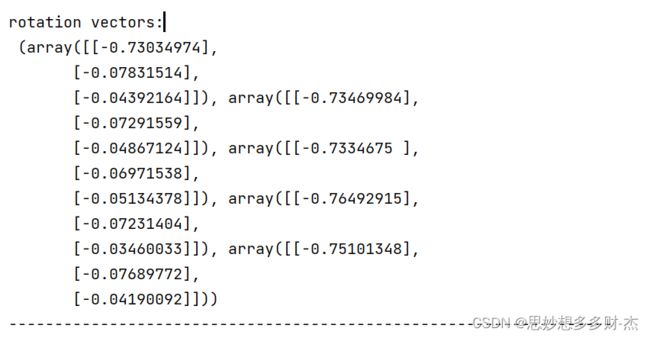
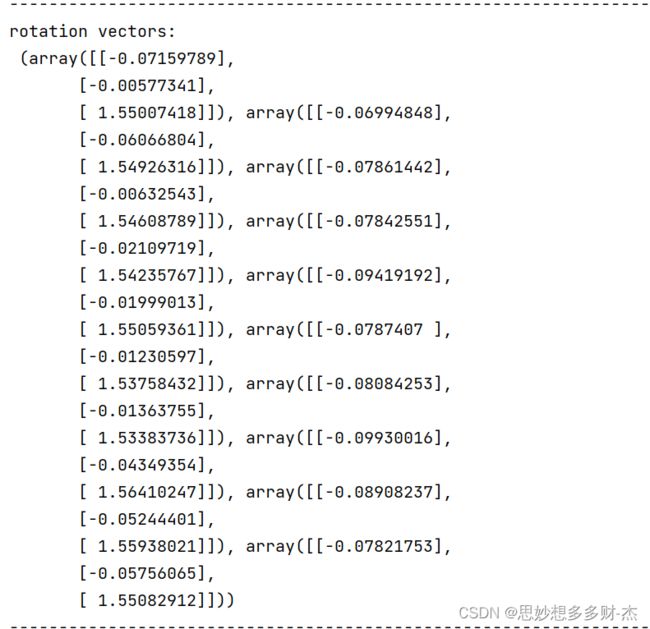
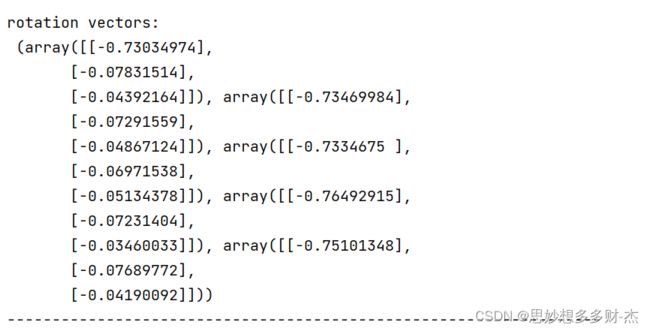
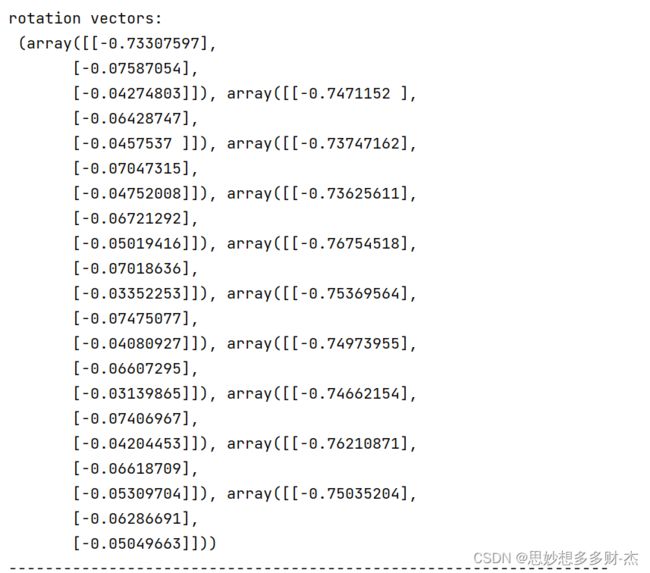
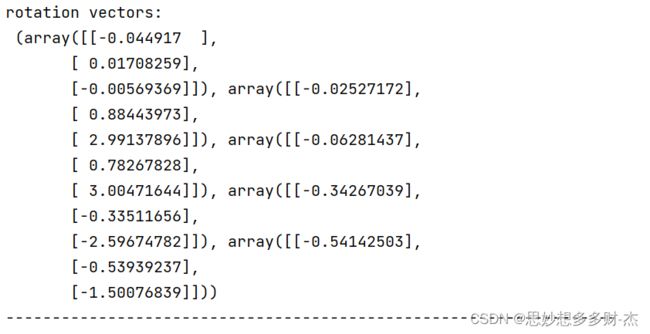
旋转矩阵

5张图片

10张图片

15张图片 

20张图片

 

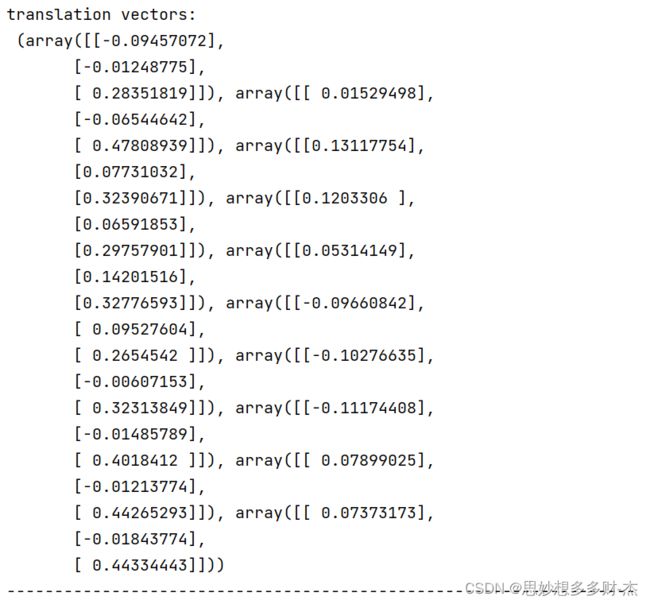
平移矩阵

5张图片

10张图片

15张图片

 

20张图片

 

反投影误差

5张图片

10张图片

15张图片

20张图片

6、总结

对于不同的图片，内参矩阵A为定值；对于同一张图片，内参矩阵A，外参矩阵(R1,R2,T)为定值；对于同一张图片上的单点，内参矩阵A，外参矩阵 (R1,R2,T)，尺度因子Z为定值。

对于同一个相机，相机的内参矩阵取决于相机的内部参数，无论标定板和相机的位置关系是怎么样的，相机的内参矩阵不变。

外参矩阵反映的是标定板和相机的位置关系。对于不同的图片，标定板和相机位置的关系有变化，所以每张图片对应的外参矩阵都是不同的。

通过反投影误差，我们可以来评估结果的好坏。越接近0，说明结果越理想。

我使用的角点形状为（9,6），角点之间的距离为0.026cm。

经过对不同拍摄角度的不同数量的实验对比，知：

1、经过相同角度的拍摄知：

（1）对于不同数量棋盘格，内参矩阵略有变化。

（2）畸变系数包含径向畸变与切向畸变，系数会随着棋盘格的数量发生变化。

（3）旋转矩阵、平移矢量针对不同的图片具有在不同数量的实验中的值略有变化。

正面10张图片中变化较大，可能时因为拍摄角度有晃动的原因。

（4）反投影误差随着我们棋盘格的数量变化不大。

2、经过不同角度的拍摄知：

（1）对于不同数量棋盘格，内参矩阵变化明显。

（2）畸变系数包含径向畸变与切向畸变，系数会随着棋盘格的不同数量的实验有变化。

（3）旋转矩阵、平移矢量针对不同的图片具有不同的值，相同的照片在不同数量的实验中，值的差异较大。

（4）反投影误差随着我们棋盘格的数量会逐渐增大。

通过反投影误差，我们可以来评估结果的好坏。越接近0，说明结果越理想。

3、由拍摄角度差异知：

无论拍摄角度、还是实验所使用的棋盘格的数量而言，内参矩阵，外参矩阵，畸变参数，反投影误差都有变化。即：每一次标定的结果都会发生变化。

每次标定的结果不同，可能的来源有这么几个:
a. 计算的内外参数的初值不同，可能因为相机标定过程中，使用迭代优化时没有收敛到最小值，只是收敛到了局部最小值。
b. 标定获得数据不稳定，标定板的大小不合适，这个影响也很大。