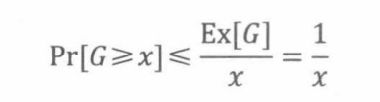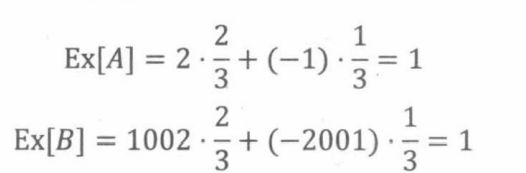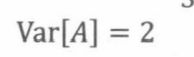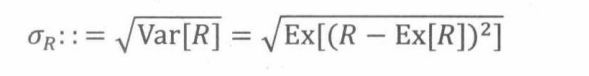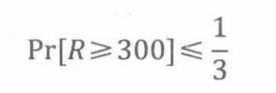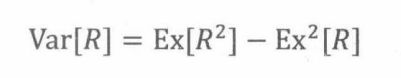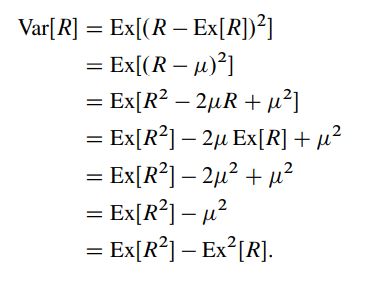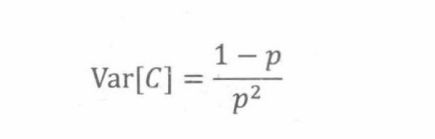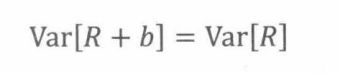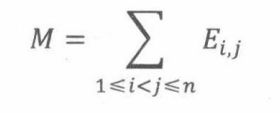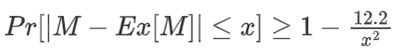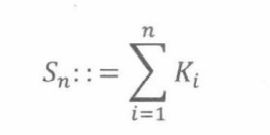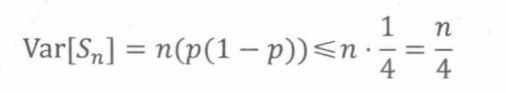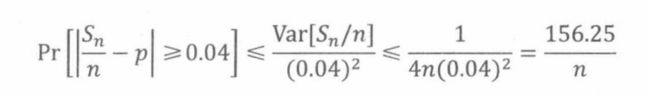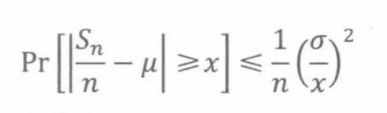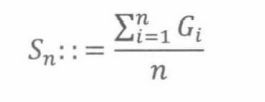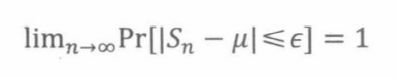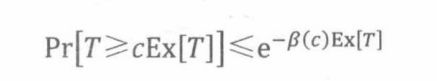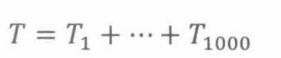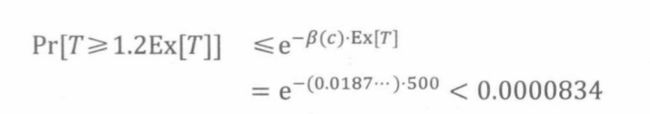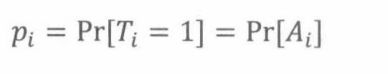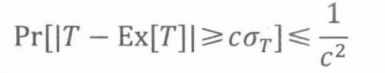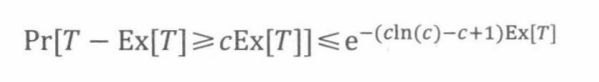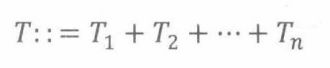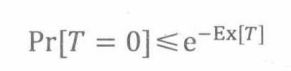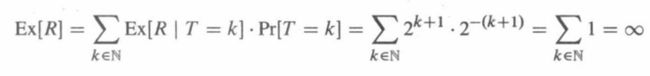第20章 离差
第20章 离差
20.1 马尔可夫定理
一般来说,马尔可夫定理能够粗略估计一个随机变量的值等于一个比它的平均值大得多的值的概率。
例子:IQ的平均值是100。我们可以得到:最多1/3的人IQ可以达到300及以上,因为如果IQ>=300的人超过1/3,则平均值必然大于(1/3)·300= 100。
定理20.1.1(马尔可夫定理)如果R是一个非负随机变量,那么对任意x >0
证明.设y为R值域上的变量,那么对任意x > 0
我们关注的是偏离平均,所以马尔可夫定理可以改写成如下形式。
推论20.1.2如果R是一个非负随机变量,那么对任意c≥1
20.1.1应用马尔可夫定理
让我们回到19.5.2节的帽子检查问题。现在,我们要知道x及以上的人拿到正确帽子的概率,即求Pr[G≥x]。
我们可以用马尔可夫定理计算上界。我们已经知道Ex[G] =1,所以根据马尔可夫定理
无论晚宴上有多少客人,有5个人拿到正确帽子的概率不超过20%。
不幸的是,马尔可夫定理不总是正确的。例如,在上面的帽子检查问题中,它给出的上界也是1/n,但实际概率是1/(n!)。对于帽子检查问题来说,马尔可夫定理给出的上界太大了。
20.1.2 有界变量的马尔可夫定理
假设我们知道MIT学生的平均IQ是150。那么,一个MIT学生的IQ超过200的概率是多少呢? 由马尔可夫定理可知:
但是,我们再看另一个事实(这可能是真的): MIT学生的IQ不低于100。令T:: = R-100,那么Ex[T] = 50。
![]()
事实上,如果对R- b而不是R应用马尔可夫定理,其中b是R的任意下界,则可以得到更好的上界。类似地,如果我们知道随机变量S的任意上界u,则u-S是非负的,那么对u-S应用马尔可夫定理,可以得到S,比它的期望小得多的概率的下界。
20.2切比雪夫定理
马尔可夫不等式也适用于事件[ R ∣ z ≥ x z ] R|^z≥x^z] R∣z≥xz]。对于正数x, z >0,该事件与事件[[R|≥x]是等价的,所以我们有如下引理。
引理 20.2.1 对任意随机变量R和正实数x,z
用离差|R一Ex[R]|重写引理20.2.1,可得
定义20.2.2随机变量R的方差( variance)为:
不等式20.4在z=2时被称为切比雪夫定理。
定理20.3.3(切比雪夫)设随机变量R及x ∈ R+,那么
20.2.1 两个赌博游戏的方差
让我们对比一下如下两个赌博游戏。
**游戏A:**以2/3的概率赢得2美元,以1/3的概率输掉1美元。
**游戏B:**以2/3的概率赢得1002美元,以1/3的概率输掉2001美元。
那么每个游戏的期望收益是多少?
两个游戏的期望收益是相等的,但这两个游戏有很大的区别。这个区别并不体现在期望上,而是体现在方差上。
游戏A的方差为2,而游戏B的方差超过了200万!这意味着游戏A的收益通常很接近期望1美元,而游戏B的收益可能偏离期望非常远。
20.2.2 标准差
定义 20.2.4随机变量R的标准差等于方差的平方根:
我们用标准差重新表述切比雪夫定理,即用 x = c σ R x = c\sigma_R x=cσR代换不等式20.1。
标准差衡量了R在其平均值附近分布的分散程度。
IQ的例子
设随机变量R为某个随机的人的IQ。那么Ex[R]= 100,op= 15,且R非负。我们要计算Pr[R≥300]。
马尔可夫定理20.1.1能给出一个粗略的边界,即
现在应用切比雪夫定理:
20.3方差的性质
20.3.1 方差公式
把期望的线性性质代入方差公式,可以得到一个很有用的公式。
引理20.3.1
对任意随机变量R成立。
证明.令u= Ex[R],则
推论20.3.2如果B是一个伯努利变量,其中p::=Pr[B=1],那么
证明.根据引理19.4.2,Ex[B]= p。但B的值只能为0和1,所以 B 2 = B B^2=B B2=B,从推论20.3.1直接可得等式20.6。
20.3.2 故障时间的方差
根据19.4.6节中的介绍,在任意给定小时内故障概率为p,平均故障时间为1/p。那么方差是多少?
所以我们只需求得 E x [ C 2 ] Ex[C^2] Ex[C2]的表达式。
19.4.6节已经使用条件期望对C进行推理求得了平均故障时间,同样的万法适用于 C 2 C^2 C2。也就是说, C 2 C^2 C2的期望是第一个小时的故障概率p乘以 1 2 1^2 12,加上第一个小时无故障的概率(1–p)乘以 ( C + 1 ) 2 (C+1)^2 (C+1)2的期望。所以
推论20.3.3如果每一步发生故障的概率为p,且相互独立,C为第一次故障发生时的步数,那么
20.3.3常数的处理
定理20.3.4 [方差的平方多重法则]令R为随机变量,a为常数。那么,
定理20.3.5令R为随机变量,b为常数,那么
标准差就是方差的平方根,所以,aR + b的标准差就是|a|乘以R的标准差。
推论20.3.6
20.3.4 和的方差
一般来说,和的方差不等于方差的和,但对于独立变量来说,二者确实相等。事实上,不一定要求相互独立:两两独立是必需的。
相互独立和两两独立?
定理20.3.7:如果R和S是独立的随机变量,那么
定理20.3.7适用于任意有限个变量的和(参见习题20.18),所以有如下定理。
定理20.3.8[方差的两两独立可加性]如果R1,R2,…,Rn是两两独立的随机变量,
那么
引理20.3.9(二项分布的方差)如果J满足参数为(n, p)的二项分布,那么
20.3.5生日匹配
假设有n个学生,一年共有d天,设M为生日匹配的学生对的数量。
并且令Eij表示第i个人和第j个人有相同生日,Eij为指示器变量,期望为1/d。
因此,M为:
算其M的期望和方差为:
特别地,当n= 95个学生,d = 365个可能的生日,Ex[M]≈12,Var[M] ≈ 12.2
根据切比雪夫定理得:
例如,当x=7时,至少有75%的可能性,学生生日匹配的对数在6到19之间。
20.4 随机抽样估计
20.4.1 选民投票
假设在选举之前的,p是偏爱某一位候选人斯科特·布朗的选民比例。我们想要估计这个未知的比例p。
现在估计p,随机选择n个选民。定义变量K1,K2,…,其中Ki表示选中的第i个选民喜欢布朗这个事件的指示器变量。各个变量相互独立,且等于1概率都是p。令Sn是它们的和,即
S n / n S_n/n Sn/n可认为是p的近似值。
假设我们希望95%的估计值与p的差值小于0.04。这意味着
这时,n应该取多少?
Sn服从二项分布。则:
接下来,我们求Sn/n的边界:
则:
则:
20.4.2两两独立采样
这里,我们不局限于1-0变量的和,或是具有相同分布的变量的和。简单来说,这个定理适用于具有相同均值和方差,但可能具有不同分布的两两独立的变量。
定理20.4.1(两两独立采样))假设 G 1 , . . . . , G n G_1,....,G_n G1,....,Gn是两两独立的变量,具有相同的均值u和方差 σ \sigma σ。定义
那么,
两两独立采样定理定量描述了随机变量的独立样本的平均数接近于均值。特别地,它证明了大数定理:选择一个足够大的样本,我们能够以任意接近100%的置信度,对均值进行任意准确的估计。
推论20.4.2[弱大数定理] 假设G1…,Gn为两两独立的变量,具有相同的均值u以及相同的有限偏差,令
那么对于任意 ϵ > 0 \epsilon>0 ϵ>0,
20.5估计的置信度
所以通常采用更通俗一点的说法。民意调查结论可以这样表述:
在95%的置信水平下,支持布朗的选民比例为1250/3125±0.04。
20.6随机变量的和
如果只知道随机变量的均值和方差,切比雪夫定理最适合做的就是确定随机变量偏离均值的概率边界。不过有时候我们知道更多的信息——例如随机变量服从二项分布,这时就可以得到更强的结论。
20.6.1引例
具体来看,Fussbook每10分钟就会收到24000条帖子。每个帖子分配给一台服务器处理,每台服务器按顺序地处理分配给它的任务。平均每条帖子要占用一台服务器1/4秒。
我们用秒衡量负载。如果一台服务器在给定时间间隔(600秒)内分配的任务超过了600秒的任务,那么这台服务器超载。
假设在理想的负载均衡条件下,10台计算机负载达到100%就可以完成这些任务。务器来应对任务耗时的随机波动以及不完美的负载均衡。
20.6.2切诺夫界
切诺夫界指出很多小的、独立的随机变量的和,不大可能显著地超出它们和的均值。
定理20.6.1(切诺夫界)设 T 1 , . . . , T n T_1,...,T_n T1,...,Tn为相互独立的随机变量,满足 0 ≤ T i ≤ 1 0≤T_i≤1 0≤Ti≤1对任意i成立。令 T = T 1 + … + T n T=T_1+…+ T_n T=T1+…+Tn,那么对所有的c≥1,,
其中B©::= clnc- c+1。
20.6.3 二项式尾的切诺夫界
独立抛1000次硬币,确定正面次数超过期望20%及以上的概率边界。令 T i T_i Ti为第i次出现正面的指示器变量。则正面的总次数为:
由以上的公式可得:
所以掷1000次硬币得到20%或更多正面的概率小于万分之一。
由于期望出现在这个上界的指数部分,所以随着抛掷的次数增加,边界迅速变小。或者说,偏离程度越大,边界越强。
20.6.4 彩票游戏的切诺夫界
在选4的彩票游戏中,你花1美元在0000到9999间选一个四位数。如果一次随机摇号选中了你的数字,那么你将赢得5000美元,中奖的概率是1/10 000。如果1000万人参加这个游戏,那么中奖者的期望是1000人。如果恰好有1000个中奖者,那么彩票发行商将从1000万的收人中拿出500万用于发奖金。彩票发行人害怕中奖人数过多,比如超过2000人,这将使他们入不敷出。那么发生这种情况的概率是多少?
令Ti为第i个人中奖的指示器变量,T=T1+…+Tn是中奖的总人数。我们选择c = 2
所以,彩票发行人几乎不可能赔钱。
20.6.5随机负载均衡
我们回到Fussbook 的负载均衡问题。我们需要确定服务器的台数m,使得在给定时间间隔内不大可能有任一服务器被分配超过600秒的负载而导致超载。
首先,我们确定第一台服务器超载的概率。设T为第一台服务器分到的负载秒数,我们要计算概率 Pr[T≥600]的上界。设 T i T_i Ti为第一台服务器花在第i个任务上的秒数,如果第i个任务被分配到了别的服务器,那么 T i = 0 T_i=0 Ti=0,否则 T i T_i Ti = 1/4。所以 T = ∑ i = 1 n T i T= \sum_{i=1}^{n}{T_i} T=∑i=1nTi就是第一台服务器的总负载,其中n = 24000。
第一台服务器的期望负载是:
所以根据切诺夫界,
其中 c = m/10
根据17.5.2节中介绍的并集的边界,有一台服务器超载的概率至多是第一台服务器超载概率的m倍。所以,
其中 c = m/10。这个上界的取值有:
20.6.6切诺夫界的证明
证明.(定理20.6.1)
引理20.6.2
证明
引理20.6.3
第二步基于这一不等式:
对[0,1]上的所有v和c≥1成立。
20.6.7边界的比较
假设有一组相互独立的事件A1,A2,…,An,我们想知道其中有多少事件可能会发生。设Ti为事件Ai的指示器随机变量,并定义
由期望的线性性质可知
根据定理20.3.8,我们还知道
马尔可夫定理告诉我们,对于任意c >1,
切比雪夫定理能给我们更强的结论:
切诺夫界给出的结论还要更强,即对于任意c > 0,
20.6.8 墨菲定律
定理20.6.4(墨菲定律)设A1,A2,…,An为相互独立的事件。令T;为A;的指示器随机变量,并定义
为发生的事件个数。那么
墨菲定律 指出,如果一个随机变量等于值为0或1的独立变量的和,并且期望值很大,那么它的值很可能大于等于1。
20.7 大期望
你独立地抛掷一枚公平的硬币。假设第一次出现正面你一共抛了k次反面。重复这个过程,如果第二次抛出正面所出现的反面次数小于等于k(失败),那么需要重新开始。直到抛出正面所出现反面的次数大于k(成功)。
我们想知道你在成功之前失败了多少次?
我们需要连续抛掷出k+1个反面才能成功,概率为2-(k+1),尝试次数的期望为2(k+1)
令R表示尝试次数的期望:
对于无限值域的随机变量,任意一个随机变量取得更大值之前的等待时间的期望是无穷。