多分类任务和 Softmax 回归

        在我们解决多类线性可分问题的时候，常会遇到单标签二分类问题、单标签多分类问题、多标签算法问题，下面分别讨论。而前面讲的线性分类模型，原则上只能解决二分类问题，但通过一些技巧就可以解决多分类问题。

1 简介

1.1 单标签二分类问题

        单标签二分类这种问题是我们最常见的算法问题，主要是指标签（label）的取值只有两种，并且算法中只有一个需要预测的label；直白来讲就是每个实例的可能类别只有两种（A or B）；此时的分类算法其实是在构建一个分类线将数据划分为两个类别。常见的算法：Logistic、SVM、KNN、决策树等。

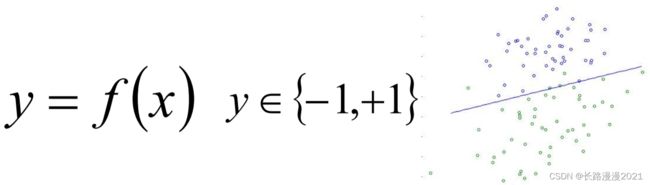
1.2 单标签多分类问题

        单标签多分类问题其实是指待预测的label只有一个，但是label的取值可能有多种情况；直白来讲就是每个实例的可能类别有 $K$ 种（$t_1,t_2,\cdots ,t_k,k\ge 3$）；常见算法：Softmax、KNN、决策树等；

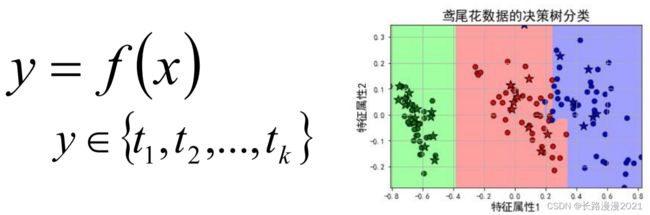
        在实际的工作中，如果是一个多分类的问题，我们可以将这个待求解的问题转换为二分类算法的延伸，即将多分类任务拆分为若干个二分类任务求解，具体的策略如下：

• One-Versus-One(OvO)：一对一
• One-Versus-All / One-Versus-the-Rest(OvA/OvR)： 一对多
• Error Correcting Output codes(纠错码机制)：多对多（MvM）

1.3 多标签算法问题

         Multi-Label Machine Learning（MLL算法）是指预测模型中存在多个 $y$ 值，具体分为两类不同情况：

• 多个待预测的 $y$ 值；
• 在分类模型中， 一个样例可能存在多个不固定的类别。

        根据多标签业务问题的复杂性，可以将问题分为两大类：

• 待预测值之间存在相互的依赖关系；
• 待预测值之间是不存在依赖关系的。

        对于这类问题的解决方案可以分为两大类：

• 转换策略(Problem Transformation Methods)；
• 算法适应(Algorithm Adaptation)。

        详细介绍，请阅读：多标签分类算法原理及代码、多分类及多标签分类算法

---

2 多分类问题

2.1 OvO

        OvO（一对一，One vs One）：假如数据 $D$ 中有 $N$ 个类别，将 $N$ 个类别进行两两配对，会得到 $N(N-1)/2$ 个二分类器。在预测中，将测试样本输入这 $N(N-1)/2$ 个二分类器中得到相应个数的预测结果，然后再将被预测结果数最多的（Voting）作为最终分类结果。

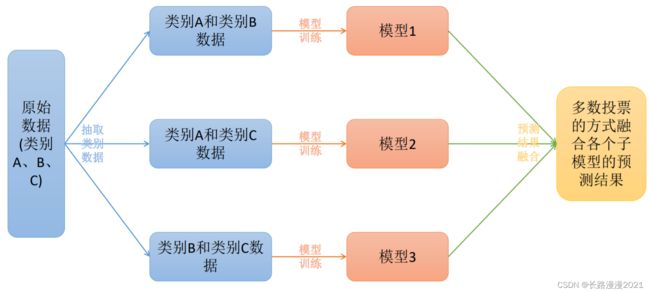
        下面举个例子，当有4个类别的时候，首先把类别两两组合（6种组合）。组合完之后，其中一个类别作为正类，另一个作为负类（这个正负只是相对而言，目的是转化为二分类）。然后对每个二分类器进行训练。可以得到6个二分类器。然后把测试样本在6个二分类器上面进行预测。从结果上可以看到，类别1被预测的最多，故测试样本属于类别1。

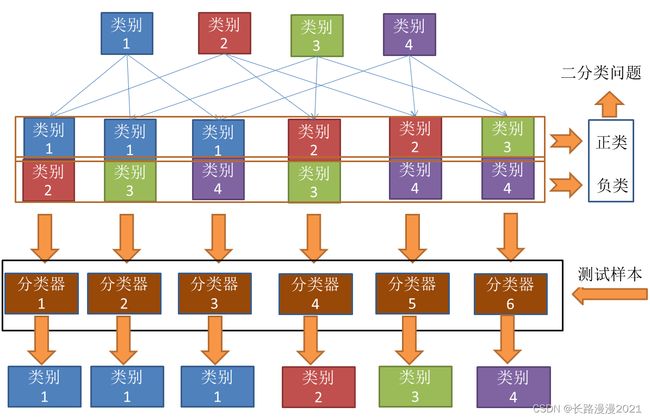
2.2 OvR

        OvR（一对其余，One vs Rest）: 将一个类别作为正例，其余所有类别作为反例，这样 $N$ 个类别可以产生 $N$ 个二分类器，将测试样本输入这些二分类器中中得到 $N$ 个预测结果，如果仅有一个分类器预测为正类，则将对应的预测结果作为最终预测结果。如果有多个分类器预测为正类，则选择置信度最大的类别作为最终分类结果。

        下面举个例子，当有4个类别的时候，每次把其中一个类别作为正类别，其余作为负类别，共有4种组合，对于这4中组合进行分类器的训练，我们可以得到4个分类器。对于测试样本，放进4个分类器进行预测，仅有一个分类器预测为正类，于是取这个分类器的结果作为预测结果，分类器2预测的结果是类别2，于是这个样本便属于类别2。

        其实，有人会有疑问，那么预测为负类的分类器就不用管了吗？是的，因为预测为负类的时候有多种可能，无法确定，只有预测为正类的时候才能唯一确定属于哪一类。比如对于分类器3，分类结果是负类，但是负类有类别1，类别2，类别4三种，到底属于哪一种？

2.3 OvO与OvR的对比

        OvR只需训练 $N$ 个分类器，而OvO需训练 $N(N-1)/2$ 个分类器， 因此，OvO的存储开销和测试时间开销通常比OvR更大。但在训练时，OvR的每个分类器均使用全部训练样例，而OvO的每个分类器仅用到两个类的样例，因此，在类别很多时，OvO的训练时间开销通常比OvR更小。至于预测性能，则取决于具体的数据分布，在多数情形下两者差不多。

综上:

• OvO的优点是，在大数据集和和类别较多的情况下，训练时间要比OvR少。缺点是，分类器个数多。
• OvR的优点是，分类器个数少，存储开销和测试时间比OvO少。缺点是，类别很多时，训练时间长。
  

补充：
        有的地方也会提到一种改进的“一对其余”方式，假设一个多分类问题的类别为 $\{1,2,\cdots ,C\}$，则共需要 $C$ 个判别函数
$$f_c(x\text{x}x;{w\text{w}w}_c)={w\text{w}w}_c^{T}x\text{x}x+b_{c}c\in \{1,\cdots ,C\}\text{\hspace{1em}(1)}$$
        对于样本 $x\text{x}x$，如果存在一个类别 $c$，相对于所有的其他类别 $\hat{c}(\hat{c}\ne c)$有 $f_c(x\text{x}x;{w\text{w}w}_c)>f_{\hat{c}}(x\text{x}x;{w\text{w}w}_{\hat{c}})$，那么 $x\text{x}x$ 属于类别 $c$。“argmax”方式的预测函数定义为
$$y=\stackrel{C}{\underset{c=1}{\mathrm{argmax}}}{f}_c(x\text{x}x;{w\text{w}w}_c)\text{\hspace{1em}(2)}$$
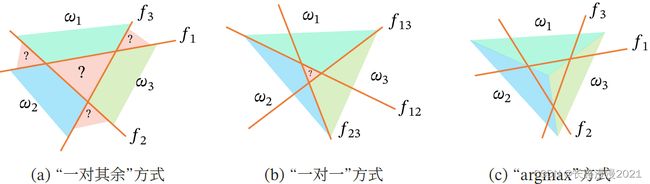
        “一对其余”方式和“一对一”方式都存在一个缺陷：特征空间中会存在一些难以确定类别的区域，而“argmax”方式很好地解决了这个问题。下图给出了用这三种方式进行多分类的示例，其中红色直线表示判别函数 $f(\cdot )=0$ 的直线，不同颜色的区域表示预测的三个类别的区域（$w_1、w_2、w_3$）和难以确定类别的区域（‘?’）。在“argmax”方式中，相邻两类 $i$ 和 $j$ 的决策边界实际上是由 $f_i(\mathbf{x};{\mathbf{w}}_i)-f_j(\mathbf{x};{\mathbf{w}}_j)=0$ 决定，其法向量为 ${\mathbf{w}}_i-{\mathbf{w}}_j$。

2.4 MvM

        MvM是每次将若干个类作为正类，若干个其他类作为反类。显然，OvO和OvR是MvM的特例。MvM的正、反类构造必须有特殊的设计，不能随意选取。这里介绍一种最常用的MvM技术"纠错输出码" (Error Correcting Output Codes，简称 ECOC)

        ECOC是将编码的思想引入类别拆分，并尽可能在解码过程中具有容错性。ECOC工作过程主要分为两步:

• 编码：对N个类别做M次划分，每次划分将一部分类别划为正类，一部分划为反类，从而形成一个二分类训练集。这样一共产生M个训练集，可训练出M个分类器。

• 解码：M 个分类器分别对测试样本进行预测，这些预测标记组成一个编码。将这个预测编码与每个类别各自的编码进行比较，返回其中距离最小的类别作为最终预测结果。

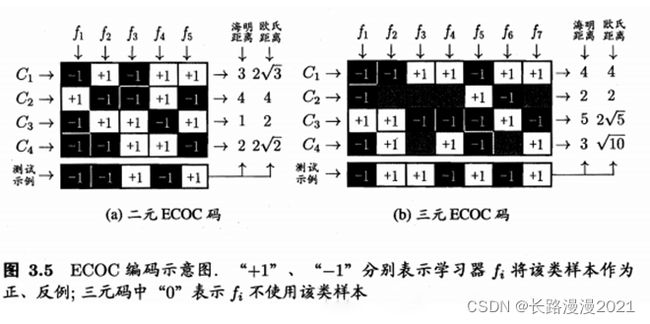
        类别划分通过"编码矩阵"指定。编码矩阵有多种形式，常见的主要有二元码和三元码。前者将每个类别分别指定为正类和反类，后者在正、反类之外，还可指定"停用类"。图3.5给出了一个示意图，在图 3.5(a) 中，分类器 $f_2$ 将 $C_l$ 类和 $C_3$ 类的样例作为正例，$C_2$ 类和 $C_4$ 类的样例作为反例；在图3.5(b)中，分类器 $f_4$ 将 $C_1$ 类和 $C_4$ 类的样例作为正例，$C_3$ 类的样例作为反例。在解码阶段，各分类器的预测结果联合起来形成了测试示例的编码，该编码与各类所对应的编码进行比较，将距离最小的编码所对应的类别作为预测结果。

        例如在图 3.5(a) 中，若基于欧式距离，预测结果将是 $C_3$。也就是一个测试样本，经过分类器 $f_1,f_2,f_3,f_4,f_5$分别预测成了(-1，-1，+1，-1，+1)，与 $C_1$ 相比较，海明距离为0+1+1+1+0=3，欧式距离为，对 $C_2,C_3,C_4$ 都进行比较即可。

2.5 Python实现

        利用sklearn的鸢尾花数据集验证一下，该数据集有 4 个特征属性，3 种分类{‘setosa’, ‘versicolor’, ‘virginica’}，下面利用 OvR、OvO和MvM三种策略进行多分类的学习及预测：

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.multiclass import OneVsRestClassifier
from sklearn.multiclass import OneVsOneClassifier
from sklearn.multiclass import OutputCodeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# 加载数据
data_iris = datasets.load_iris()
x, y = data_iris.data, data_iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3,random_state = 0)

# 使用multiclass的OvO多分类策略,分类器使用LogisticRegression
model = OneVsOneClassifier(LogisticRegression(C=1.0, tol=1e-6))
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
print(accuracy_score(y_test, y_pred))
# 准确率为：0.9777777777777777


# 使用multiclass的OvR多分类策略,分类器使用LogisticRegression
model = OneVsRestClassifier(LogisticRegression(C=1.0, tol=1e-6))
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
print(accuracy_score(y_test, y_pred))
# 准确率为：0.9555555555555556

# 使用multiclass的ECOC多分类策略,分类器使用LogisticRegression
# 模型对象创建
# code_size: 指定最终使用多少个子模型，实际的子模型的数量=int(code_size*label_number)
# code_size设置为1，等价于ovr子模型个数；
# 设置为0~1, 那相当于使用比较少的数据划分，效果比ovr差; 
# 设置为大于1的值，那么相当于存在部分模型冗余的情况
model = OutputCodeClassifier(LogisticRegression(C=1.0, tol=1e-6), code_size=30, random_state=0)
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
print(accuracy_score(y_test, y_pred))
# 准确率为：0.9555555555555556

        注意：OvR、OvO和MvM不是逻辑回归专有的，也可以运用与SVM等只能解决二分类问题的模型上。

---

3 Softmax 回归

        softmax回归其实是逻辑回归的一种变形，逻辑回归模型输出的是两种类别的概率，softmax回归输出的 $K$ 种类别的概率。模型公式如下：
$$h_{\mathbf{\theta }}\left({\mathbf{x}}_i\right)=\left[\begin{array}{c}p\left(y_i=1|{\mathbf{x}}_i;\mathbf{\theta }\right)\\ p\left(y_i=2|{\mathbf{x}}_i;\mathbf{\theta }\right)\\ ⋮\\ p\left(y_i=k|{\mathbf{x}}_i;\mathbf{\theta }\right)\end{array}\right]=\frac{1}{{\sum }_{j=1}^k{e}^{{\mathbf{\theta }}_j^T{\mathbf{x}}_i}}\left[\begin{array}{c}{e}^{{\mathbf{\theta }}_1^T{\mathbf{x}}_i}\\ e^{{\mathbf{\theta }}_2^T{\mathbf{x}}_i}\\ ⋮\\ e^{{\mathbf{\theta }}_k^T{\mathbf{x}}_i}\end{array}\right]\text{\hspace{1em}(3)}$$

        参数 $\theta \text{θ}\theta$ 是一个矩阵，矩阵的每一行可以看做是一个类别所对应分类器的参数，总共有 $K$ 行，输出的 $K$ 个数就表示该类别的概率，总和为1。这样，softmax回归模型对于一个测试样本，可以得到多个类别对应的概率值，模型选取概率最高的类别作为最终判定结果。详细介绍：Softmax 回归原理与实现

        在sklearn中使用softmax回归还是调用linear.model.LogisticRegression，设置一下multi_class参数即可，内部即会使用softmax函数计算出每个类别的概率。

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# 加载数据
data_iris = datasets.load_iris()
x, y = data_iris.data, data_iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.3, random_state = 0)

# 采用softmax回归进行分类
model = LogisticRegression(C=1.0, tol=1e-6, multi_class='multinomial', solver='newton-cg')
model.fit(x_train, y_train)
y_pred = model.predict(x_test)
print(accuracy_score(y_test, y_pred))
# 准确率为：0.9777777777777777

# 输出每个测试样例的类别预测概率
print (model.predict_proba(x_test))

        多个二分类器策略和softmax回归的区别
        softmax回归中对一个测试样本得到的属于各类别的概率和一定为1，而多个二分类器策略中，不管是OvO、OvR还是MvM策略，一个样本在多个二分类器上得到的概率和不一定为 1。因此当分类之间是互斥的情况下（e.g 数字手写识别、动物识别），通常采用softmax回归；而目标类别不是互斥时（e.g 华语音乐、流行音乐、重金属音乐等）则采用多个二分类器策略进行预测。

---

参考

• 多分类及多标签分类算法：https://www.cnblogs.com/us-wjz/articles/11410118.html
• 机器学习中的多分类任务详解：https://blog.csdn.net/anshuai_aw1/article/details/82973039
• 逻辑回归的多分类：https://www.infoq.cn/article/NoPHBaCaxPwOkYgrsBEv
• 二分类、多分类与多标签问题的区别：https://juejin.cn/post/6844903630479294477