YOLOv5 中 metrics.py 之 ap_per_class && compute_ap 学习记录

目录

参数部分：

 tp(correct): shape=[25268, 10] bool       

 conf: shape=[25268]        

pred_cls: shape=[25268]  

target_cls: shape=[929]

unique_classes: shape=[71]

n_l && n_p: shape=254 && shape=4488

fpc: shape=[4488,10]

 tpc: shape=[4488,10]

 recall: shape=[4488,10]

 precision: shape=[4488,10]

mpre: shape=[4490]

mrec: shape=[4490]

ap: shape=[71,10]

p: shape=[71,1000]

R: shape=[71,1000]

代码部分：

reference：

---

整整花了一天的时间在看，原本准备2小时搞懂（太天真了）

参数部分：

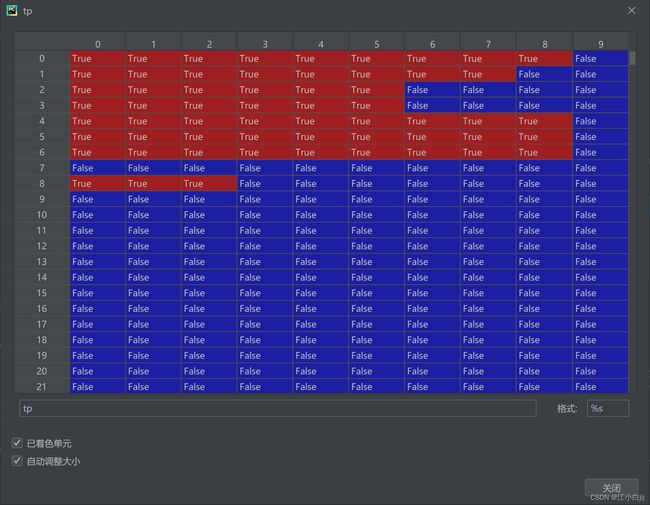
 tp(correct): shape=[25268, 10] bool       

含义：整个数据集所有图片中所有预测框在每一个iou条件下(0.5~0.95)10个是否是TP

old_view：

        这里的tp中的预测框（每行）是按图片为单位进行存储的（比如说前300行属于第一张图片，300行到500行属于第二张图片）。

new_view:

        这里利用np.argsort对conf进行排序（从大到小） 得到新的tp。

 conf: shape=[25268]        

含义：整个数据集所有图片的所有预测框的conf

old_view：

        同理这里也是按图片为单位进行存储的。      

new_view:

        这是经过排序后的conf。 

pred_cls: shape=[25268]  

含义：整个数据集所有图片的所有预测框的类别

old_view:

        同理这里也是按图片为单位进行存储的。 

new_view:    

        同理，这是经过conf排序后的类别。

注意：这里的tp、conf、pred_cls是一一对应的

target_cls: shape=[929]

含义：整个数据集所有图片的所有gt框的类别

view:

unique_classes: shape=[71]

含义：整个数据集中一共包含了71个类别（CoCo128中）

view:

n_l && n_p: shape=254 && shape=4488

含义：整个数据集gt框中c类别的框数目；所有预测框中c类别的框数目

view:

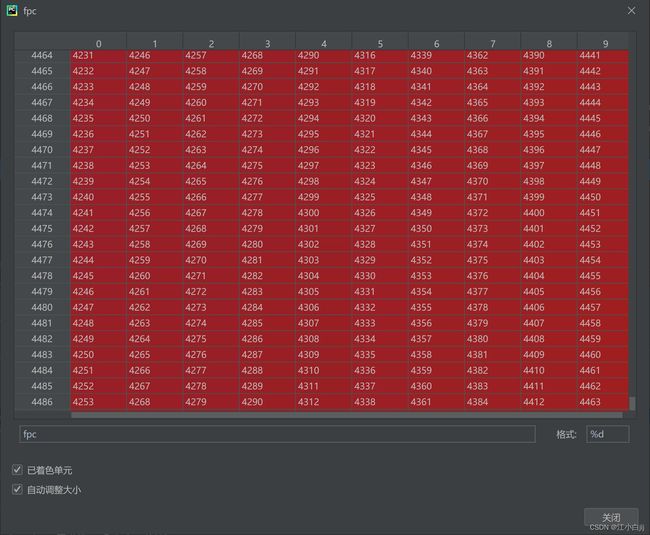
fpc: shape=[4488,10]

含义：匹配tp中类别为c 顺序按置信度从大到小排列 截至到每一个预测框的各个iou阈值下FP个数 最后一行表示c类在该iou阈值下所有FP个数。

view:

        由于使用np.cumsum(),所以对每一行进行累加操作，又由于conf从大到小排序，导致经过最后置信度低的预测框fp的个数基本都会增加。使得view呈现从左到右依次增加，从上到下依次增加的趋势。

 tpc: shape=[4488,10]

含义：匹配tp中类别为c 顺序按置信度排列，截至到每一个预测框的各个iou阈值下TP个数 最后一行表示c类在该iou阈值下所有TP数。

view:

         随着iou阈值的变大（同一行），对于同一个预测框检测的tp是逐步减少，又由于随着检测框的增多（同一列），检测到的tp会不断增多，使得view呈现从左到右依次减小，从上到下依次增加的趋势。

 recall: shape=[4488,10]

含义：类别为c，顺序按置信度排列，截至每一个预测框的各个iou阈值下的召回率。

view:

        就是将前面的tpc除以n_l（number of labels）。

 precision: shape=[4488,10]

含义：类别为c，顺序按置信度排列，截至每一个预测框的各个iou阈值下的精确率

view:

        precision = tpc / (tpc + fpc)  

mpre: shape=[4490]

含义：该参数通过np.concatenate 返回 [开头 + 输入precision（排序后) + 末尾]

view:

        mpre添加了开头和末尾从4488变为了4490，它取自于precision的c类别下的某一iou列，所以shape为[4490]，这里原本经过np.concatenate会变为行向量，但后面经过排序又变为了列向量，这就是计算ap是的y坐标。

mrec: shape=[4490]

含义：该参数通过np.concatenate返回 开头 + 输入recall + 末尾

view:

        同理mrec通过添加开头和末尾从4488变为了4490，它取自recall的c类别下的某一iou列，所以shape为[4490]，经过np.concatenate变为了行向量，用于计算ap的x坐标。

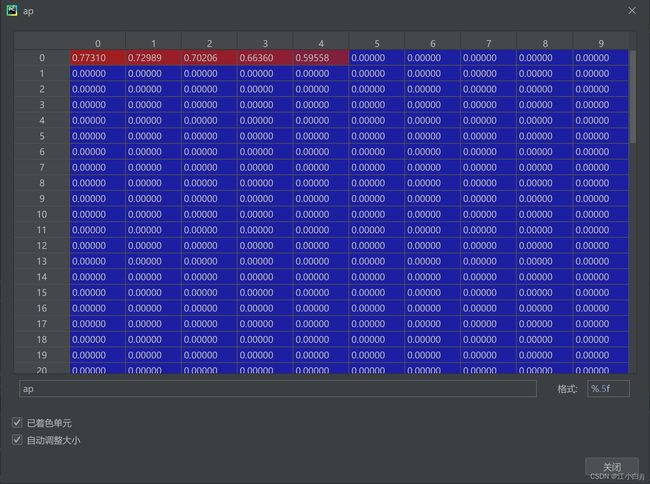
ap: shape=[71,10]

含义：表示某类别在某个iou下的AP（指的是以mrec为X轴，mpre为Y轴，围成曲线的面积，也是PR图）

view:

        shape[71,10]表示71个类别以及各iou（0.5-0.95总共10个），ap越大越好。

p: shape=[71,1000]

含义：指的是所有类别, 横坐标为conf(值为px=[0, 1, 1000] 0~1 1000个点)对应的precision值

view:

        每一行代表每一个类别，利用np.interp取得在（0-1）之间1000的插值，用于绘制P-Confidence（注意，这里的Map取值可以手动设置，默认是Map=0.5）

R: shape=[71,1000]

含义：指的是所有类别, 横坐标为conf(值为px=[0, 1, 1000] 0~1 1000个点)对应的recall值

view:

        每一行代表每一个类别，利用np.interp取得在（0-1）之间1000的插值，用于绘制P-Confidence（注意，这里的Map取值可以手动设置，默认是Map=0.5）

代码部分：

def ap_per_class(tp, conf, pred_cls, target_cls, plot=False, save_dir='.', names=()):
    """用于val.py中计算每个类的mAP
       计算每一个类的AP指标(average precision)还可以 绘制P-R曲线
       mAP基本概念: https://www.bilibili.com/video/BV1ez4y1X7g2
       Source: https://github.com/rafaelpadilla/Object-Detection-Metrics.
       :params tp(correct): [pred_sum, 10]=[1905, 10] bool 整个数据集所有图片中所有预测框在每一个iou条件下(0.5~0.95)10个是否是TP
       :params conf: [img_sum]=[1905] 整个数据集所有图片的所有预测框的conf
       :params pred_cls: [img_sum]=[1905] 整个数据集所有图片的所有预测框的类别
               这里的tp、conf、pred_cls是一一对应的
       :params target_cls: [gt_sum]=[929] 整个数据集所有图片的所有gt框的class
       :params plot: bool
       :params save_dir: runs\train\exp30
       :params names: dict{key(class_index):value(class_name)} 获取数据集所有类别的index和对应类名
       :return p[:, i]: [nc] 最大平均f1时每个类别的precision
       :return r[:, i]: [nc] 最大平均f1时每个类别的recall
       :return ap: [71, 10] 数据集每个类别在10个iou阈值下的mAP
       :return f1[:, i]: [nc] 最大平均f1时每个类别的f1
       :return unique_classes.astype('int32'): [nc] 返回数据集中所有的类别index
       """

    # Sort by objectness
    #  np.argsort（将x中的元素从小到大排列，提取其对应的index(索引)，这里添加负号其实是从大到小）
    # 计算mAP 需要将tp按照conf降序排列
    i = np.argsort(-conf)
    # 得到重新排序后对应的 tp, conf, pre_cls
    tp, conf, pred_cls = tp[i], conf[i], pred_cls[i]

    # Find unique classes  对类别去重, 因为计算ap是对每类进行
    unique_classes = np.unique(target_cls)
    nc = unique_classes.shape[0]  # number of classes, number of detections

    # Create Precision-Recall curve and compute AP for each class
    # px: [0, 1] 中间间隔1000个点 x坐标(用于绘制P-Conf、R-Conf、F1-Conf)
    # py: y坐标[] 用于绘制IOU=0.5时的PR曲线
    px, py = np.linspace(0, 1, 1000), []  # for plotting
    # 初始化 对每一个类别在每一个IOU阈值下 计算AP P R   ap=[nc, 10]  p=[nc, 1000] r=[nc, 1000]
    ap, p, r = np.zeros((nc, tp.shape[1])), np.zeros((nc, 1000)), np.zeros((nc, 1000))
    for ci, c in enumerate(unique_classes):
        # i: 记录着所有预测框是否是c类别框   是c类对应位置为True, 否则为False
        i = pred_cls == c
        # n_l: gt框中的c类别框数量
        n_l = (target_cls == c).sum()
        # n_p: 预测框中c类别的框数量# number of labels
        n_p = i.sum()  # number of predictions

        # 如果没有预测到 或者 ground truth没有标注 则略过类别c
        if n_p == 0 or n_l == 0:
            continue
        else:
            # Accumulate FPs(False Positive) and TPs(Ture Positive)   FP + TP = all_detections
            # tp[i] 可以根据i中的的True/False觉定是否删除这个数  所有tp中属于类c的预测框
            #       如: tp=[0,1,0,1] i=[True,False,False,True] b=tp[i]  => b=[0,1]
            # a.cumsum(0)  会按照对象进行列方向累加操作
            # 一维按行累加如: a=[0,1,0,1]  b = a.cumsum(0) => b=[0,1,1,2]   而二维则按列累加
            # fpc: 类别为c 顺序按置信度排列 截至到每一个预测框的各个iou阈值下FP个数 最后一行表示c类在该iou阈值下所有FP数
            # tpc: 类别为c 顺序按置信度排列 截至到每一个预测框的各个iou阈值下TP个数 最后一行表示c类在该iou阈值下所有TP数
            fpc = (1 - tp[i]).cumsum(0)
            tpc = tp[i].cumsum(0)

            # Recall=TP/(TP+FN)  加一个1e-16的目的是防止分母为0
            # n_l=TP+FN=num_gt: c类的gt个数=预测是c类而且预测正确+预测不是c类但是其实属于c类
            # recall: 类别为c 顺序按置信度排列 截至每一个预测框的各个iou阈值下的召回率
            recall = tpc / (n_l + 1e-16)  # recall curve
            # 返回所有类别, 横坐标为conf(值为px=[0, 1, 1000] 0~1 1000个点)对应的recall值  r=[nc, 1000]  每一行从大到小
            # 这里 recall[:, 0] 指的是iou=0.5时的R-Confidence
            r[ci] = np.interp(-px, -conf[i], recall[:, 0], left=0)  # negative x, xp because xp decreases
            # print(-conf[i])
            # print(-px)

            # Precision=TP/(TP+FP)
            # precision: 类别为c 顺序按置信度排列 截至每一个预测框的各个iou阈值下的精确率
            precision = tpc / (tpc + fpc)  # precision curve
            # 返回所有类别, 横坐标为conf(值为px=[0, 1, 1000] 0~1 1000个点)对应的precision值  p=[nc, 1000]
            # 总体上是从小到大 但是细节上有点起伏 如: 0.91503 0.91558 0.90968 0.91026 0.90446 0.90506
            # 这里 precision[:, 0] 指的是iou=0.5时的P-Confidence
            p[ci] = np.interp(-px, -conf[i], precision[:, 0], left=1)  # p at pr_score

            # AP from recall-precision curve
            # 对c类别, 分别计算每一个iou阈值(0.5~0.95 10个)下的mAP
            for j in range(tp.shape[1]):
                # 这里执行10次计算ci这个类别在所有mAP阈值下的平均mAP  ap[nc, 10]
                ap[ci, j], mpre, mrec = compute_ap(recall[:, j], precision[:, j])
                if plot and j == 0:
                    # py: 用于绘制每一个类别IOU=0.5时的PR曲线
                    py.append(np.interp(px, mrec, mpre))  # precision at [email protected]

    # 计算F1分数 P和R的调和平均值  综合评价指标
    # 我们希望的是P和R两个越大越好, 但是P和R常常是两个冲突的变量, 经常是P越大R越小, 或者R越大P越小 所以我们引入F1综合指标
    # 不同任务的重点不一样, 有些任务希望P越大越好, 有些任务希望R越大越好, 有些任务希望两者都大, 这时候就看F1这个综合指标了
    # 返回所有类别, 横坐标为conf(值为px=[0, 1, 1000] 0~1 1000个点)对应的f1值  f1=[nc, 1000]
    f1 = 2 * p * r / (p + r + 1e-16)

    # 画各种曲线图
    if plot:
        plot_pr_curve(px, py, ap, Path(save_dir) / 'PR_curve.png', names)
        plot_mc_curve(px, f1, Path(save_dir) / 'F1_curve.png', names, ylabel='F1')
        plot_mc_curve(px, p, Path(save_dir) / 'P_curve.png', names, ylabel='Precision')
        plot_mc_curve(px, r, Path(save_dir) / 'R_curve.png', names, ylabel='Recall')

    # f1=[nc, 1000]   f1.mean(0)=[1000]求出所有类别在x轴每个conf点上的平均f1
    # .argmax(): 求出每个点平均f1中最大的f1对应conf点的index
    i = f1.mean(0).argmax()  # max F1 index
    return p[:, i], r[:, i], ap, f1[:, i], unique_classes.astype('int32')


def compute_ap(recall, precision):
    """
    用于ap_per_class函数中
    计算某个类别在某个iou阈值下的mAP
    Compute the average precision, given the recall and precision curves
    :params recall: (list) [1635] 在某个iou阈值下某个类别所有的预测框的recall  一直从小到大
                      (每个预测框的recall都是截至到这个预测框为止的总recall)
    :params precision: (list) [1635] 在某个iou阈值下某个类别所有的预测框的precision
                         总体上是从大到小 但是细节上有点起伏 如: 0.91503 0.91558 0.90968 0.91026 0.90446 0.90506
                         (每个预测框的precision都是截至到这个预测框为止的总precision)
    :return ap: Average precision 返回某类别在某个iou下的mAP(均值) [1]
    :return mpre: precision curve [1637] 返回 开头 + 输入precision(排序后) + 末尾
    :return mrec: recall curve [1637] 返回 开头 + 输入recall + 末尾
    """
    # 在开头和末尾添加保护值 防止全零的情况出现 value Append sentinel values to beginning and end
    # np.concatenate 默认是按行进行拼接（0表示行，1表示列） 这里由列向量变成了行向量
    # https://blog.csdn.net/qq_38150441/article/details/80488800
    mrec = np.concatenate(([0.], recall, [recall[-1] + 0.01]))
    mpre = np.concatenate(([1.], precision, [0.]))

    # Compute the precision envelope  np.flip翻转顺序
    # np.flip(mpre): 把一维数组每个元素的顺序进行翻转 第一个翻转成为最后一个
    # np.maximum.accumulate(np.flip(mpre)): 计算数组(或数组的特定轴)的累积最大值 令mpre是单调的 从小到大
    # np.flip(np.maximum.accumulate(np.flip(mpre))): 从大到小
    # 到这大概看明白了这步的目的: 要保证mpre是从大到小单调的(左右可以相同)
    # 我觉得这样可能是为了更好计算mAP 因为如果一直起起伏伏太难算了(x间隔很小就是一个矩形)
    # 而且这样做误差也不会很大 两个之间的数都是间隔很小的
    # 这里又从行向量变为列向量
    mpre = np.flip(np.maximum.accumulate(np.flip(mpre)))

    # Integrate area under curve
    method = 'interp'  # methods: 'continuous', 'interp'
    if method == 'interp':
        # 用一些典型的间断点来计算AP
        x = np.linspace(0, 1, 101)  # 101-point interp (COCO)
        #  np.trapz(list,list) 计算两个list对应点与点之间四边形的面积 以定积分形式估算AP 第一个参数是y 第二个参数是x
        # 这里画个图就很清楚了（定积分思想）
        ap = np.trapz(np.interp(x, mrec, mpre), x)  # integrate
    else:  # 'continuous'
        # 采用连续的方法计算AP
        # 通过错位的方式 判断哪个点当前位置到下一个位置值发生改变 并通过！=判断 返回一个布尔数组
        i = np.where(mrec[1:] != mrec[:-1])[0]  # points where x axis (recall) changes
        # 值改变了就求出当前矩阵的面积  值没变就说明当前矩阵和下一个矩阵的高相等所有可以合并计算
        ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])  # area under curve

    return ap, mpre, mrec

        代码部分注释的很详细了，还有不懂得可以自行百度。

reference：

【YOLOV5-5.x 源码解读】metrics.py_满船清梦压星河HK的博客-CSDN博客_metrics.py

np.trapz(): np.trapz()的生动解释_鲁凡 Fan Lu的博客-CSDN博客_numpy trapz

np.interp(): numpy.interp()用法_MrLittleDog的博客-CSDN博客_np.interp

np.cumsum(): numpy.cumsum — NumPy v1.22 Manual

np.maximum.accumulate(): 【python numpy】a.cumsum()、np.interp()、np.maximum.accumulate()、np.trapz()_满船清梦压星河HK的博客-CSDN博客_np.maximum.accumulate用法