【C初阶】C初阶考试题

家人们欢迎来到小姜的世界，<<点此>>传送门 这里有详细的关于C/C++/Linux等的解析课程，家人们赶紧冲鸭！！！

---

一、选择题

（一）递归

A 41
B 67
C 109
D 177

解析：答案是B，这题目是递归很麻烦，每传递一次就需要增加一次cnt，所以根据画图或者手算fib数列能够得到其结果是67。

（二）后置++发生死循环

解析：答案选D，x++和x–都是先使用再运算，所以是当x=1进去以后，先输出1，再往下运算的时候x加一变成2，而x–的操作是赋值操作，要的是结果，此时x变成1，在括号里面一直是>0的数，所以是死循环。

（三）后置++运算

解析：答案选C。此题需要注意的是输出的是i和j，i++是先使用再运算，所以，i的本身的值赋给j，j先是1，而i在使用完以后就是需要自增1，所以i的值为1。

（四）操作符运算

解析：答案选A。*=是先把=后面的值运算完再和k相乘，所以原式等价于k=k*(i+j)。

（五）全局变量与生命周期

解析：答案选A。如果函数内的局部变量和全局变量同名，那么在函数内部局部变量会屏蔽全局变量，使用的是局部变量。因为函数有声明周期，当遇到最后一个花括号后函数生命周期结束。因此本题中 test 函数内全局变量 a 被局部变量 a 屏蔽。对 a 的修改不会对全局变量 a 带来任何影响。所以全局变量 a 的值保持为 1。

（六）操作符知识

解析：答案选C。我们看A选项中文是或者，所以操作符是||，B选项中switch语句中不一定要含有default，但一般是需要的，C选项是正确的，D选项中单分支是可以的。

（七）主函数的位置

解析：答案选C。main函数是可以放在任意地方的，但一个程序只能放一个。

（八）主函数main

解析：答案选D。A选项是正确的，C源程序中可以由很多个函数组成，B选项是正确的，一个C源程序是需要包含一个main主函数的，C选项也是正确的，D选项中注释说明可以用在多条语句后面。

（九）C语言程序

解析：答案选C。C语言本身是没有输入输出语句，在标准库中提供了输出输出语句。

（十）do……while语句

解析：答案选C。do……while语句是不管三七二十一先进行一次运算，再看条件，当我们看，进入内部以后，c的值是-1，a的值变成-1，值已经发生改变了，而此时的判断条件是a=-1<0不成立，然后跳出循环了。

（十一）double浮点型运算

解析：答案为D。x是double型的，3/2输出的是整型，答案是1，而y的值本身就是一个double型的，所以y的值为2.000000+1=3.000000。

（十二）for循环的循环次数

解析：答案选C。=是赋值的意思，所以y=123是恒成立的，所以只需要看x<4的条件即可，所以是循环4次。

（十三）取地址

解析：答案选D。由题可知指针p是指向变量year的，*p等价于year
A选项 等价于year+=1，因此year=1010;
B选项 先算括号里的，等价于year++，year=1010;
C选项 先算括号里的，等价于++year，year=1010;
D选项 单目运算符从右至左，先地址++，再取值；

（十四）|操作符

解析：答案选A。

（十五）类型相加减

解析：答案选D。自动类型转换就是编译器默默地、隐式地、偷偷地进行的数据类型转换，这种转换不需要程序员干预，会自动发生。
1.将一种类型的数据赋值给另外一种类型的变量时就会发生自动类型转换，如： float f = 100; 100 是 int 类型，会自动转换成 float，再赋值给 f。
2.在不同类型的混合运算中，编译器也会自动地转换数据类型，将参与运算的所有数据先转换为同一种类型，然后再进行计算。转换的规则如下：
a.转换按数据长度增加的方向进行，以保证数值不失真，或者精度不降低。例如，int 和 long 参与运算时，先把 int 类型的数据转成 long 类型后再进行运算。
所有的浮点运算都是以双精度进行的，即使运算中只有 float 类型，也要先转换为 double 类型，才能进行运算。
char 和 short 参与运算时，必须先转换成 int 类型。

二、编程题

（一）求最小公倍数

1.题目描述

正整数A和正整数B 的最小公倍数是指 能被A和B整除的最小的正整数值，设计一个算法，求输入A和B的最小公倍数。
数据范围：

输入描述：

输出描述：

示例1：
输入
5 7
输出
35
输入两个正整数A和B。
输出A和B的最小公倍数。

2.解题思路

最小公倍数：是指能同时被a和b整除的最小正整数。
思路1：赋给最大值法（算法较慢）。先将a和b中最大值赋给min，再min往后++，直到这个min能够整除a和b，这个min的值就是a和b的最小公倍数。
思路2：辗转相除法。利用最大公约数去求解，最小公倍数就是a*b的值除以最大公约数。分三种情况。第一种情况，当两个数互质的话，最小公约数就是这两个数相乘除以1（最大公倍数）即可；第二种情况，一个数是另一个数的倍数，那最小公倍数就是这两个数中的最大值，就是两个数相乘除以最大公因数；第三种情况，两者不成倍数但有共同的因子，那就跟第二种算法一样，相乘再除以最大公因数。如何理解辗转相除法呢，我们来三个例子解析一下：
例子一：4 16 ---- 16mod4=4所以最大公因数直接就是4。
例子二：32 20 ---- 我们在两个元素中找相同的元素，如果想要找相同的元素，那就需要一直进行取模运算，32和20经过第一次取模运算余的是12，所以32就可以转换成为20+12了，发现第一次运算完还没结束，20是两者共有的因子，而12是多出来的数，所以我们需要找第二步运算，继续找因子，所以我们需要把20拆开，那就取模12余8，进行完第二步以后，32变成12+12+8,20变成12+8，有共有的因子12和8，但是最大公因数那可是只能有一个，所以继续找因子，用12mod8余数为4，所以32和20变成8个4相加和5个4相加，那这个4不就是这两个数的共有的因子，所以4为最大公因数。

例子三、2 3
思路3：判断(i*a)modb。

3.解题代码

//方法一、从最大值往后一个一个试
#include

int main() {
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	int min = 0;
	if (a > b)
		min = a;
	else
		min = b;
	while (min) {
		if (min % a == 0 && min % b == 0) {
			printf("最小公倍数是:%d\n", min);
			break;
		}
		min++;
	}

	return 0;
}

//方法二、辗转相除法
#include
int main() {
	int a = 0;
	int b = 0;
	scanf("%d %d", &a, &b);
	int sum = a * b;
	int m = 0;
	while (m = a % b) { 
		a = b;
		b = m;
	}
	printf("%d", sum / b);
	return 0;
}

//方法三、判断(i*a)modb。
#include
int main() {
	int a = 0;
	int b = 0;
	int i = 1;
	scanf("%d %d", &a, &b);
	while ((i * a) % b != 0) {
		i++;
	}
	printf("%d\n", i * a);
	return 0;
}

（二）倒置字符串

1.题目描述

将一句话的单词进行倒置，标点不倒置。比如 I like beijing. 经过函数后变为：beijing. like I
输入描述：
每个测试输入包含1个测试用例： I like beijing. 输入用例长度不超过100
输出描述：
依次输出倒置之后的字符串,以空格分割
示例1：
输入
I like beijing.
输出
beijing. like

2.解题思路

方法是先整体逆序，再去找单个单词进行逆序，那其实如果单纯中间没有空格那很简单了（如图1），直接定义left和right指针进行逆序即可，那事不随人愿，中间肯定是需要空格的，那我们开开心心的想那每个单词中间只有一个空格呢？那需要想一想了，那我们只需要把头指针和尾指针都往后移动一位到都指向单词第一位然后重复操作即可，但是事又不随人愿了，中间不免不小心多打了好几个空格怎么办呢？这就需要思考了，那是不是只要我们加个条件，先我们碰到空格的时候俩指针都不动，直接进入逆序，耍逆序函数一次，后面再进行end和start指针都往后一位再去判断是不是空格，要还是空格，那继续逆序一次，即保持空格不动，一直到我们start和end指针都找到不是空格和’\0’即可，然后继续逆序就好了。

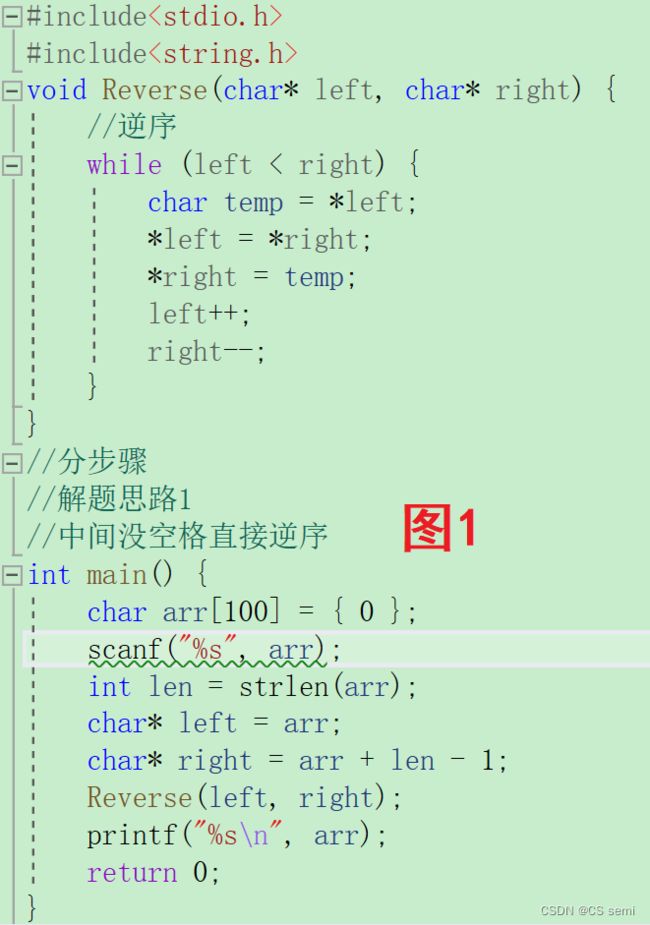
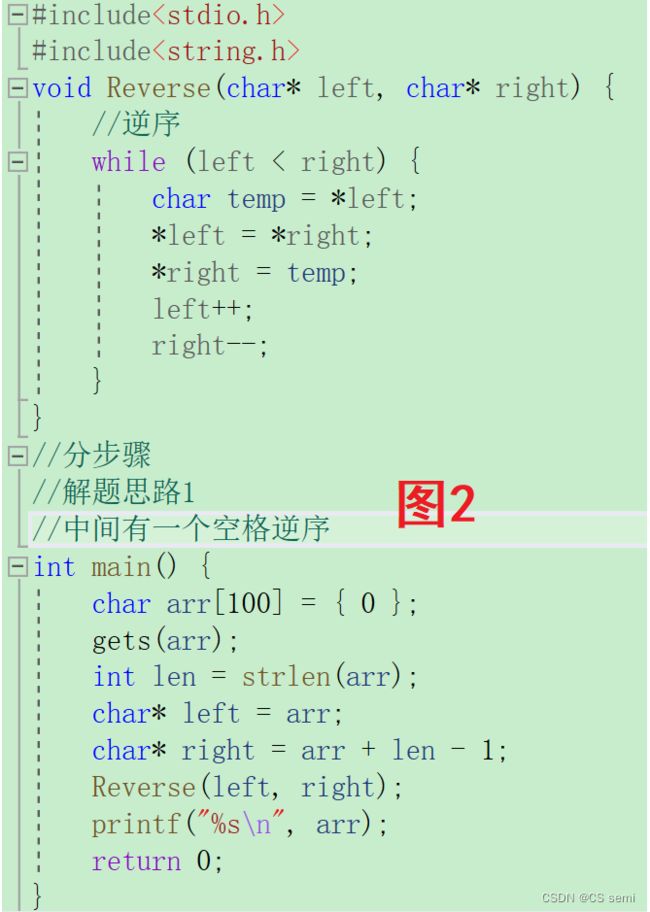
3.解题代码

#include
#include

void Reverse(char* left, char* right) {
	//逆序
	while (left < right) {
		char temp = *left;
		*left = *right;
		*right = temp;
		left++;
		right--;
	}
}

int main() {
	char arr[100] = { 0 };
	gets(arr);
	//求字符串长度
	int len = strlen(arr);
	//先整体逆序
	Reverse(arr, arr + len - 1);
	printf("%s\n", arr);
	//定义头指针和尾指针都指向的第一个字符串位置
	char* start = arr;
	char* end = arr;
	//再逐个单词逆序
	//用end指针往后移动碰到'\0'和空格以前为一个单词
	while (*end != '\0') {//大条件end指针一直到'\0'
		while (*end != '\0' && *end != ' ') {
			//进入循环，end指针不等于'\0'和空格则end指针加1
			end++;
		}
		Reverse(start, end - 1);//倒置单个字符串
		start = end + 1;//保证start指针在end的后一位
		if (*end != '\0') {
			//此时保证end指针和start指针指向的是一个位置
			end++;
		}
	}
	printf("%s\n", arr);
	return 0;
}

---

总结

这些题目很常规，不是非常的难，考验的就是基础知识的掌握，当大家觉得题目很难的时候，要慢慢仔仔细细地进行剖析，不可一口气吃个胖子，在做这些题目的时候应当认认真真仔仔细细，看清楚条件和问题以及代码需要做些什么。