题解系列013 + 比赛系列003 | CSDN 第十一届编程竞赛题解 + 建议

一、总体情况

得分：25+25+25+25=100（主页显示是 16m 作答时间，但实际作答时间是 52m17s，排列第 7 位）

题目评价：前三题十分基础，第四题虽有一定思维难度，但相比传统的第四题仍有一些差距。当然，本次题解的重心也会放在第 4 题。

二、题目分析

第一题

题目

分析

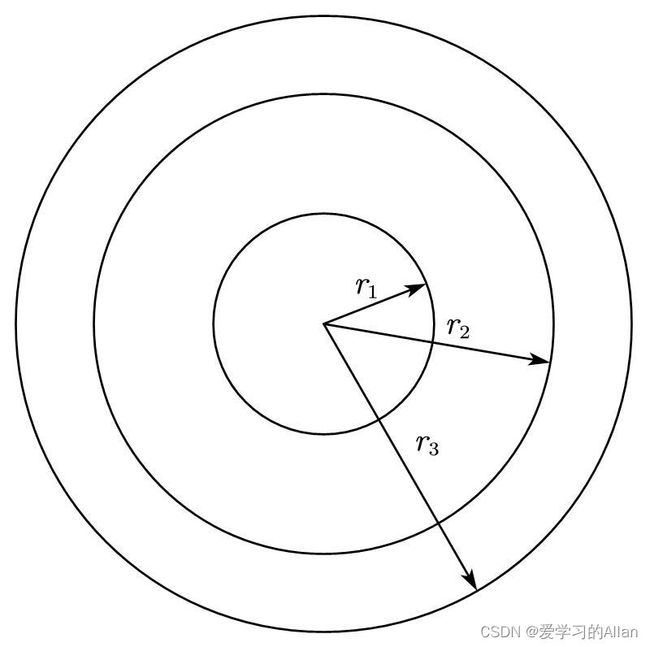
1. 注意到输入数据的顺序是随机的，所以第一步是要对数组进行排序，从而确定同心圆的相对位置。
2. 假设半径从小到大分别为 $r_1<r_2<\cdots <r_n(n\in {\mathbb{Z}}^{+})$，则所求结果为$$S=r_n^2-r_{n-1}^2+r_{n-2}^2-r_{n-3}^2+\cdots +{\left(-1\right)}^{n-2}{r}_2^2+{\left(-1\right)}^{n-2}{r}_1^2$$
3. 因此我们分奇偶讨论，容易用 for 循环和 if 判断得出答案。
4. 注意按照题目要求保留小数在 python 中不能用简单的 round（会自动省略 0），而是使用更为规范的通配表达式 "{:.3f}".format()来实现。

程序

#1
import math
class Solution:
    def __init__(self) -> None:
        pass
    
    def solution(self, n, arr):
        result = 0

        sorted_arr = arr.sort()
        
        for i in range(n-1, -1, -1):
            if (n-1-i)%2==0:
                result = result + math.pi*(arr[i]**2)
            elif (n-1-i)%2==1:
                result = result - math.pi*(arr[i]**2)
        return "{:.3f}".format(result)

if __name__ == "__main__":


    n = int(input().strip())
    
    
    arr = [int(item) for item in input().strip().split()]
    
    
    sol = Solution()
    result = sol.solution(n, arr)

    print(result)

第二题

题目

分析

此题难度与第一题相近，均属于入门难度。我们只需要判断并维护最小值即可。

代码

#2
class Solution:
    def __init__(self) -> None:
        pass
    
    def solution(self, n, m, k, arr):
        result = None
        
        maxi = n+1
        for i in range(n):
            if arr[i]<=k and i!=m-1 and arr[i]!=0:
                maxi = min(maxi, abs(i-m+1))
        result = maxi

        return result

if __name__ == "__main__":


    
    arr_temp = [int(item) for item in input().strip().split()]
    
    n = int(arr_temp[0])
    m = int(arr_temp[1])
    k = int(arr_temp[2])
    
    arr = [int(item) for item in input().strip().split()]
    
    
    sol = Solution()
    result = sol.solution(n, m, k, arr)

    print(result)

第三题

题目

分析

CSDN 竞赛为什么这么喜欢考 DP 啊……
这是一道 DP 经典问题 —— 背包问题。度娘上即有相应的解答，在此不再赘述。

程序

#3
class Solution:
    def __init__(self) -> None:
        pass
    
    def solution(self, n, M, vector):
        result = None

        dp = [0 for i in range(1100)]
        
        for i in range(1, n+1):
            for j in range(M, vector[i-1][0]-1, -1):
                dp[j] = max(dp[j], dp[j-vector[i-1][0]]+vector[i-1][1])
        result = dp[M]

        return result

if __name__ == "__main__":


    
    arr_temp = [int(item) for item in input().strip().split()]
    
    n = int(arr_temp[0])
    M = int(arr_temp[1])
    
    vector = []
    for i in range(n):
        vector.append([int(item) for item in input().strip().split()])
    
    
    sol = Solution()
    result = sol.solution(n, M, vector)

    print(result)

第四题

题目

分析

虽然已经有不少参赛者指出这是一道陈题（Codeforces 上面就有），但就题目本身而言，这题是本场比赛最有价值的一道题。这题的关键在于不要纠结于局部，而是注重整体。这也是许多看似复杂困难的问题的解法。我们通过追问的方式给出我的思考过程。

• Q1：座位的排布是否有某种规律？
• A1：可以分成一段段，段与段之间由客人隔开。
• Q2：既然要求最小值，那段数能否先把它搞到最小？
• A2：很遗憾不行。但幸运的是，段数是一个定值。具体而言，每一个圆桌上如果有 $m\in [1,N]$ 个人，那么也将有 $m$ 个段（圆排列的性质），因此总段数 $=N$。
• Q3：那是否有哪些段“阻碍”了最小化？
• A3：如果某个乘客的舒适空间特别大，那么这一段的最小长度就要大于等于它的舒适空间（非严格表述）。
• Q4：那么怎么省空间呢？
• A4：只能左右把空位“抵消”掉，从而分担掉一点舒适空间。

至此，我们已经可以给出一个数学化的表述：假设一个人的左舒适空间为 $l_i,1\le i\le N$, 右舒适空间为 $r_i,1\le i\le N$, $\sigma$ 为 $\{1,2,\cdots ,N\}$ 上的任一置换, 则问题的一种局部解为 $\sum _{i=1}^n\max \{l_i,r_{\sigma (i)}\}+\underset{\text{加上一开始的 N 个人}}{N}$。这里若 ${\sigma }^g(i)=i$, 那么就成了一个圈（$1\le g\le N$），简单来说，这种状态一定能构造出来。

容易看出，为了使上式达到最小值，应该让大的和大的配，小的和小的配（直观上也很显然，严格的数学证明只要写一个 $2\times N$ 阵列去分析就行）。于是如果将 $\left\{l_i\right\},\left\{r_i\right\}$ 排序为 $r_1\ge r_2\ge \cdots \ge r_N,l_1\ge l_2\ge \cdots \ge l_N$, 则所求的 $N+\min \{\sum _{i=1}^n\max \{l_i,r_{\sigma (i)}\}\}=N+\sum _{i=1}^n\max \{l_i,r_i\}$。剩下的代码是容易的。

代码

class Solution:
    def __init__(self) -> None:
        pass
    
    def solution(self, n, vector):
        left = [vector[i][0] for i in range(n)]
        right = [vector[i][1] for i in range(n)]
        
        left.sort()
        right.sort()
        
        result = n
        for i in range(n):
            result = result + max(left[i], right[i])
        
        return result

if __name__ == "__main__":


    n = int(input().strip())
    
    
    vector = []
    for i in range(n):
        vector.append([int(item) for item in input().strip().split()])
    
    
    sol = Solution()
    result = sol.solution(n, vector)

    print(result)

---

欢迎关注我的博客！

我的 GitHub 账号: 欢迎 Fork + PR!

我的洛谷账号：这是我

我的洛谷团队：这是我的团队

欢迎大家关注我，在项目上与我协作哦！