并查集专题
普通的并查集:
pku 1308 Is It A Tree?
http://poj.org/problem?id=1308
判断点的关系是否满足是一棵树,这里考察细节,注意:1:空的也是树;2:注意可能形成森林,森林就不是所描述的树了
 View Code
View Code
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <queue> #include <stack> #include <set> #include <map> #include <string> #define CL(a,num) memset((a),(num),sizeof(a)) #define iabs(x) ((x) > 0 ? (x) : -(x)) #define Min(a , b) ((a) < (b) ? (a) : (b)) #define Max(a , b) ((a) > (b) ? (a) : (b)) #define ll __int64 #define inf 0x7f7f7f7f #define MOD 100000007 #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define test puts("<------------------->") #define maxn 100007 #define M 100007 #define N 100007 using namespace std; //freopen("din.txt","r",stdin); int f[N]; bool flag; bool vt[N]; int cs[N]; void init(){ for (int i = 0; i < N; ++i){ f[i] = i; vt[i] = false; } } int find(int x){ if (x != f[x]) f[x] = find(f[x]); return f[x]; } void Union(int x,int y){ int tx = find(x); int ty = find(y); if (tx != ty) f[ty] = tx; else flag = true; } int main(){ //freopen("din.txt","r",stdin); int x,y,i; int cas = 1; int len; while (~scanf("%d%d",&x,&y)){ if (x == -1 && y == -1) break; if (x == 0 && y == 0){ printf("Case %d is a tree.\n",cas++); continue; } len = 0; flag = false; init(); if (!vt[x]){vt[x] = true; cs[len++] = x;} if (!vt[y]){vt[y] = true; cs[len++] = y;} Union(x,y); while (scanf("%d%d",&x,&y)){ if (!x && !y) break; if (!vt[x]){vt[x] = true; cs[len++] = x;} if (!vt[y]){vt[y] = true; cs[len++] = y;} if (!flag) Union(x,y); } if (!flag){ int rt = find(cs[0]); for (i = 1; i < len; ++i){ if (rt != find(cs[i])){ flag = true; break; } } } if (!flag) printf("Case %d is a tree.\n",cas++); else printf("Case %d is not a tree.\n",cas++); } return 0; }
pku 2236 Wireless Network
http://poj.org/problem?id=2236
题意:
给出n个电脑的坐标,给出两种操作,O x表示将第x个电脑修好, S x,y表示询问第x个电脑是否可以与第y个电脑通信。 通信的要求:两台电脑必须都已经修好,而且两台电脑的距离小于d。两台电脑之间的距离可以通过中间点来缩小。 比如A 与 B 可以通信 B 与 C 可以通信 ,则A与C的距离为0 。
首先用isok标记每台电脑是否被修好,当我们修好电脑i时,在寻找与他距离小于d的已经好得电脑的集合并加入到该集合。这样就保证了,能够通信的电脑都放到了同一集合中。
最后查看是否属于同一集合即可.
 View Code
View Code
#include <iostream> #include <cstdio> #include <cmath> #include <vector> #include <cstring> #include <algorithm> #include <string> #include <set> #include <functional> #include <numeric> #include <sstream> #include <stack> #include <map> #include <queue> #define CL(arr, val) memset(arr, val, sizeof(arr)) #define ll long long #define inf 0x7f7f7f7f #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define ll long long #define L(x) (x) << 1 #define R(x) (x) << 1 | 1 #define MID(l, r) (l + r) >> 1 #define Min(x, y) (x) < (y) ? (x) : (y) #define Max(x, y) (x) < (y) ? (y) : (x) #define E(x) (1 << (x)) #define iabs(x) (x) < 0 ? -(x) : (x) #define OUT(x) printf("%I64d\n", x) #define lowbit(x) (x)&(-x) #define Read() freopen("din.txt", "r", stdin) #define Write() freopen("dout.txt", "w", stdout); #define N 1007 #define M 1007 using namespace std; struct ipoint { double x,y; }pt[N]; int f[N]; bool isok[N]; int n; double d; double dis(int i,int j) { double x = pt[i].x - pt[j].x; double y = pt[i].y - pt[j].y; double s = sqrt(x*x + y*y); return s; } int find(int x) { if (f[x] != x) f[x] = find(f[x]); return f[x]; } void Union(int x,int y) { x = find(x); y = find(y); if (x != y) f[x] = y; } int main() { int i; char op[3]; int x,y; scanf("%d%lf",&n,&d); for (i = 0; i < n; ++i) { f[i] = i; isok[i] = false; scanf("%lf%lf",&pt[i].x,&pt[i].y); } f[n] = n; isok[n] = false; while (~scanf("%s%d",op,&x)) { if (op[0] == 'O') { isok[x] = true; for (i = 1; i <= n; ++i) { if (dis(i - 1,x - 1) <= d && isok[i] && i != x) { // printf("******%d %d\n",i,x); Union(i,x); } } } else { scanf("%d",&y); int tx = find(x); int ty = find(y); if (tx != ty) { printf("FAIL\n"); } else { printf("SUCCESS\n"); } } // for (i = 1; i <= n; ++i) // { // printf(">%d %d\n",i,find(i)); // } } return 0; }
pku 2524
http://poj.org/problem?id=2524
裸的简单并查集:判断集合的个数
pku 1861
http://poj.org/problem?id=1861
Kruscal应用,它不仅保证了得到的是最小生成树,而且还保证了,每条边肯定选择的是最小的。
关系并查集:
pku 1703 Find them, Catch them
http://poj.org/problem?id=1703
题意:
总共存在两个帮派,有两种操作D [a] [b] 说明a,b属于不同的帮派,A [a] [b] 需要我们来判断他们的关系,属于同一帮派输出,属于不同的帮派,或者不确定。
思路:
利用并查集构成的树的长度关系,我们把不同的利用并查集合并,然后维持一个他们到根节点的距离dep我们只要判断他们的距离的差值是否为2的倍数就可判断时代否在同以帮派了。
 View Code
View Code
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <queue> #include <stack> #include <set> #include <map> #include <string> #define CL(a,num) memset((a),(num),sizeof(a)) #define iabs(x) ((x) > 0 ? (x) : -(x)) #define Min(a , b) ((a) < (b) ? (a) : (b)) #define Max(a , b) ((a) > (b) ? (a) : (b)) #define ll __int64 #define inf 0x7f7f7f7f #define MOD 100000007 #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define test puts("<------------------->") #define maxn 100007 #define M 100007 #define N 100007 using namespace std; //freopen("din.txt","r",stdin); int dep[N],f[N]; int n; //初始化 void init(){ int i; for (i = 0; i <= n; ++i){ f[i] = i; dep[i] = 0; } } //find函数里面维护dep int find(int x){ if (x != f[x]){ int tmp = f[x]; f[x] = find(f[x]); dep[x] = (dep[tmp] + dep[x])%2;//更新未压缩的点,保持dep的正确性 } return f[x]; } void Union(int x,int y){ int tx = find(x); int ty = find(y); if (tx != ty){ f[ty] = tx; dep[ty] = (dep[x] + dep[y] + 1)%2;//维护根节点的正确性 } } int main(){ //freopen("din.txt","r",stdin); int i; int T,m; char op[3]; int x,y; scanf("%d",&T); while (T--){ scanf("%d%d",&n,&m); init(); for (i = 0; i < m; ++i){ scanf("%s%d%d",op,&x,&y); if (op[0] == 'D'){ Union(x,y); } else{ int tx = find(x); int ty = find(y); if (tx != ty) printf("Not sure yet.\n"); else{ if (iabs(dep[x] - dep[y])%2 == 0) printf("In the same gang.\n"); else printf("In different gangs.\n"); } } } } return 0; }
pku 1182 食物链
http://poj.org/problem?id=1182
题意:中文略
思路:
这个理还是根据长度来确定他们的关系:父是子的关系:0:同类,1:食物,2:天敌。
当他们不属于同一集合时,合并:
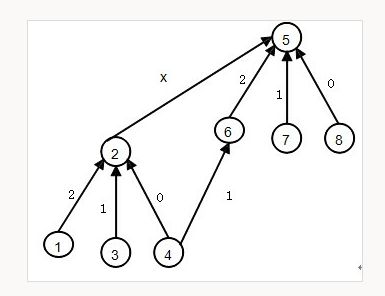
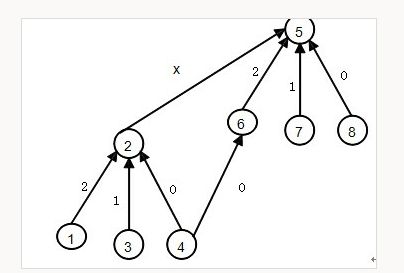
例如4,6是食物关系,则有0 + x = 1 + 2 我们可以退出x,y是食物关系时,有dep[fx] = dep[y] + 1 - dep[x];
若是同类关系则有 0 + x = 0 + 2 则可推出 dep[fx] = dep[y] + 0 - dep[x];
然后就是在find里面维护dep了。
 View Code
View Code
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <queue> #include <stack> #include <set> #include <map> #include <string> #define CL(a,num) memset((a),(num),sizeof(a)) #define iabs(x) ((x) > 0 ? (x) : -(x)) #define Min(a , b) ((a) < (b) ? (a) : (b)) #define Max(a , b) ((a) > (b) ? (a) : (b)) #define ll __int64 #define inf 0x7f7f7f7f #define MOD 100000007 #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define test puts("<------------------->") #define maxn 100007 #define M 100007 #define N 100007 using namespace std; //freopen("din.txt","r",stdin); int dep[N],f[N]; int n,k; int ct; void init(){ int i; for (i = 0; i <= n; ++i){ f[i] = i; dep[i] = 0; } } int find(int x){ if (x != f[x]){ int tmp = f[x]; f[x] = find(f[x]); dep[x] = (dep[x] + dep[tmp])%3; } return f[x]; } void Union(int x,int y,int mk){ int tx = find(x); int ty = find(y); if (tx != ty){ f[tx] = ty; dep[tx] = (dep[y] + mk - dep[x])%3;//维护dep数组 } else{ if ((dep[x] - dep[y] + 3)%3 != mk) ct++; } } int main(){ // freopen("din.txt","r",stdin); ct = 0; int op,x,y; scanf("%d%d",&n,&k); init(); while (k--){ scanf("%d%d%d",&op,&x,&y); if (x > n || y > n || (op == 2 && x == y)){ ct++; continue; } if (op == 1){ Union(x,y,0);//同类合并时,间距为0 } else{ Union(x,y,1);//不是关系时,间距为1 } } printf("%d\n",ct); return 0; }
pku 2492
http://poj.org/problem?id=2492
关系并查集的水题,要么属于1要么属于0.和1703一样的。。
 View Code
View Code
#include <iostream> #include <cstdio> #include <cmath> #include <vector> #include <cstring> #include <algorithm> #include <string> #include <set> #include <functional> #include <numeric> #include <sstream> #include <stack> #include <map> #include <queue> #define CL(arr, val) memset(arr, val, sizeof(arr)) #define ll long long #define inf 0x7f7f7f7f #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define ll long long #define L(x) (x) << 1 #define R(x) (x) << 1 | 1 #define MID(l, r) (l + r) >> 1 #define Min(x, y) (x) < (y) ? (x) : (y) #define Max(x, y) (x) < (y) ? (y) : (x) #define E(x) (1 << (x)) #define iabs(x) (x) < 0 ? -(x) : (x) #define OUT(x) printf("%I64d\n", x) #define lowbit(x) (x)&(-x) #define Read() freopen("din.txt", "r", stdin) #define Write() freopen("dout.txt", "w", stdout); #define N 2007 #define M 2007 using namespace std; int f[N],dep[N]; int n,m; int find(int x) { int fa = 0; if (f[x] != x) { fa = f[x]; f[x] = find(f[x]); dep[x] = (dep[x] + dep[fa])%2; } return f[x]; } int main() { int i; int x,y; int T,cas = 1; scanf("%d",&T); while (T--) { scanf("%d%d",&n,&m); for (i = 1; i <= n; ++i) f[i] = i,dep[i] = 0; bool flag = false; while (m--) { scanf("%d%d",&x,&y); if (!flag) { int tx = find(x); int ty = find(y); if (tx != ty) { f[tx] = ty; dep[tx] = (dep[y] + 1 - dep[x])%2; } else { if ((iabs(dep[x] - dep[y]))%2 == 0) { flag = true; } } } } printf("Scenario #%d:\n",cas++); if (flag) printf("Suspicious bugs found!\n"); else printf("No suspicious bugs found!\n"); printf("\n"); } return 0; }
pku 1733 Parity game
http://poj.org/problem?id=1733
题意:
给定长度为n的序列,每个位置i要么是0要么是1,给出一些该序列的信息, x,y,res 表示在[x,y]这个区间里里面存在偶数个1还是奇数个1。让我们依据信息往下走判断信息的正确性,直到遇到错误信息跳出,然后输出在出错之前正确的信息个数。
思路:
这道题目并查集确实不好想,我的思路是记录每个信息x与y的关系,每次都根据距离根结点的长度来判断x与y的关系,可是当有[1,2] [3,4] [5,6]时[1,6]之间的关系是确定的,可是单纯记录x,y的关系的话,是不能确定他们之间的关系的。所以我们要向前一步记录[x-1,y]的关系,这样就保证了,最后他们的根节点都可归结于0,[1,2][3,4]确定关系后,[1,4]肯定能够确定关系了。
 View Code
View Code
#include <iostream> #include <cstdio> #include <cmath> #include <vector> #include <cstring> #include <algorithm> #include <string> #include <set> #include <functional> #include <numeric> #include <sstream> #include <stack> #include <map> #include <queue> #define CL(arr, val) memset(arr, val, sizeof(arr)) #define ll long long #define inf 0x7f7f7f7f #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define ll long long #define L(x) (x) << 1 #define R(x) (x) << 1 | 1 #define MID(l, r) (l + r) >> 1 #define Min(x, y) (x) < (y) ? (x) : (y) #define Max(x, y) (x) < (y) ? (y) : (x) #define E(x) (1 << (x)) #define iabs(x) (x) < 0 ? -(x) : (x) #define OUT(x) printf("%I64d\n", x) #define lowbit(x) (x)&(-x) #define Read() freopen("din.txt", "r", stdin) #define Write() freopen("dout.txt", "w", stdout); #define N 5007 #define M 15007 using namespace std; struct node { int x,y; char res[10]; }nd[N]; int a[2*N],len,f[2*N],dep[2*N]; int n; void init(int m) { for (int i = 0; i <= m; ++i) { f[i] = i; dep[i] = 0; } } int Search(int l,int r,int val) { while (l <= r) { int mid = (l + r)/2; if (a[mid] == val) return mid; else if (a[mid] > val) r = mid - 1; else l = mid + 1; } return -1; } int find(int x) { int fa = 0; if (f[x] != x) { fa = f[x]; f[x] = find(f[x]); dep[x] = (dep[x] + dep[fa])%2; } return f[x]; } int cmp(int a,int b) { return a < b; } int main() { // Read(); int i; scanf("%d",&n); scanf("%d",&n); len = 1; for (i = 0; i < n; ++i) { scanf("%d%d%s",&nd[i].x,&nd[i].y,nd[i].res); a[len++] = nd[i].x; a[len++] = nd[i].y; } sort(a + 1,a + len,cmp);//这里的长度是len-1 int tn = 1; for (i = 2; i < len; ++i) if (a[i] != a[i - 1]) a[++tn] = a[i]; init(tn); int ans = 0; for (i = 0; i < n; ++i) { int x = Search(1,tn,nd[i].x); int y = Search(1,tn,nd[i].y); x--; int tx = find(x); int ty = find(y); int add = 0; if (nd[i].res[0] == 'e') add = 0; else add = 1; if (tx != ty) { f[ty] = tx; dep[ty] = (dep[x] + add - dep[y])%2; } else { if ((iabs(dep[y] - dep[x]))%2 != add) break; } ans++; } printf("%d\n",ans); return 0; }
HDU 3038 How Many Answers Are Wrong
http://acm.hdu.edu.cn/showproblem.php?pid=3038
同上题类似的题目,只不过改成了求和。。
 View Code
View Code
#include <iostream> #include <cstdio> #include <cmath> #include <vector> #include <cstring> #include <algorithm> #include <string> #include <set> #include <functional> #include <numeric> #include <sstream> #include <stack> #include <map> #include <queue> #define CL(arr, val) memset(arr, val, sizeof(arr)) #define ll __int64 #define inf 0x7f7f7f7f #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define L(x) (x) << 1 #define R(x) (x) << 1 | 1 #define MID(l, r) (l + r) >> 1 #define Min(x, y) (x) < (y) ? (x) : (y) #define Max(x, y) (x) < (y) ? (y) : (x) #define E(x) (1 << (x)) #define iabs(x) (x) < 0 ? -(x) : (x) #define OUT(x) printf("%I64d\n", x) #define lowbit(x) (x)&(-x) #define Read() freopen("din.txt", "r", stdin) #define Write() freopen("dout.txt", "w", stdout); #define N 200007 #define M 15007 using namespace std; int n,m; int f[N]; ll dep[N]; void init(int len) { for (int i = 0; i <= len; ++i) { f[i] = i; dep[i] = 0; } } int find(int x) { int fa = 0; if (f[x] != x) { fa = f[x]; f[x] = find(f[x]); dep[x] = (dep[x] + dep[fa]); } return f[x]; } int main() { // Read(); int x,y,w; while (~scanf("%d%d",&n,&m)) { init(n); int ans = 0; while (m--) { scanf("%d%d%d",&x,&y,&w); x--; int tx = find(x); int ty = find(y); if (tx != ty) { f[ty] = tx; dep[ty] = (dep[x] + w - dep[y]); } else { if (iabs(dep[y] - dep[x]) != w) ans++; } } printf("%d\n",ans); } return 0; }
pku 1417 True Liars
http://poj.org/problem?id=1417
题意:
一伙人中有p1个诚实的人,p2个说谎的人,诚实的人总是说实话,说谎的人总是说谎话。给出n个询问,x,y,string,表示问x,y是不是诚实的人,string(yes,no)。求是否能够唯一确定这p1个诚实的人,如果能输出者n个人,否则输出no.
思路:
由于诚实的人总是说真话,说谎的人总是说谎话。这里的人要么是诚实的,要么是是说谎的,当出现yes时,肯定x,y属于同一类人,出现no时,x,y属于不同类的人。根据这个利用并查集将p1+p2个人进行合并分组,每一组都会分成两种,一种是诚实人的个数,一种是说谎人的个数。然后利用DP求到达dp[len][p1]时,是否只有一种方法,即可。len表示分分出的组数,dp[i][j]表示到达第i个分组时有j个诚实的人的方法数。
ps:这里遇到个问题,不知道为什么,并查集处理的时候我的的 dep[tx] = (dep[y] + add - dep[x])%2; dep[x] = (dep[x] + dep[fa])%2;处理WA, 改成d ep[tx] = dep[y]^dep[x]^add; dep[x] = dep[x]^dep[fa];就对了呢?不过我觉得是一样的思想啊,不知为何。
 View Code
View Code
#include <iostream> #include <cstdio> #include <cmath> #include <vector> #include <cstring> #include <algorithm> #include <string> #include <set> #include <functional> #include <numeric> #include <sstream> #include <stack> #include <map> #include <queue> #define CL(arr, val) memset(arr, val, sizeof(arr)) #define ll __int64 #define inf 0x7f7f7f7f #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define L(x) (x) << 1 #define R(x) (x) << 1 | 1 #define MID(l, r) (l + r) >> 1 #define Min(x, y) (x) < (y) ? (x) : (y) #define Max(x, y) (x) < (y) ? (y) : (x) #define E(x) (1 << (x)) #define iabs(x) (x) < 0 ? -(x) : (x) #define OUT(x) printf("%I64d\n", x) #define lowbit(x) (x)&(-x) #define Read() freopen("din.txt", "r", stdin) #define Write() freopen("dout.txt", "w", stdout); #define N 602 #define M 15007 using namespace std; int a[N][2]; int f[N],dep[N]; int len,n,p1,p2; vector<int>ivc[N][2],ans; int root[N]; int dp[N][N],pre[N][N]; void init(int m) { for (int i = 0; i <= m; ++i) { f[i] = i; dep[i] = 0; ivc[i][0].clear(); ivc[i][1].clear(); } } int find(int x) { int fa = 0; if (f[x] != x) { fa = f[x]; f[x] = find(f[x]); dep[x] = dep[x]^dep[fa]; } return f[x]; } void Union(int x,int y,int add) { int tx = find(x); int ty = find(y); if (tx != ty) { f[tx] = ty; dep[tx] = dep[y]^dep[x]^add; } } int main() { // Read(); int i,j; int x,y; char res[5]; while (~scanf("%d%d%d",&n,&p1,&p2)) { if (!n && !p1 && !p2) break; init(p1 + p2); for (i = 0; i < n; ++i) { scanf("%d%d%s",&x,&y,res); if (res[0] == 'n') Union(x,y,1); else Union(x,y,0); } len = 0; CL(a,0); for (i = 1; i <= p1 + p2; ++i) { if (find(i) == i) { root[++len] = i; for (j = 1; j <= p1 + p2; ++j) { if (find(j) == i) { // printf("*****%d\n",dep[j]); a[len][dep[j]]++; ivc[len][dep[j]].push_back(j); } } } } CL(dp,0); CL(pre,0); dp[0][0] = 1; for (i = 1; i <= len; ++i) { for (j = 0; j <= p1; ++j) { if (j >= a[i][0]) { dp[i][j] += dp[i - 1][j - a[i][0]]; if (dp[i - 1][j - a[i][0]] == 1) pre[i][j] = 0; } if (j >= a[i][1]) { dp[i][j] += dp[i - 1][j - a[i][1]]; if (dp[i - 1][j - a[i][1]] == 1) pre[i][j] = 1; } } } // printf(">>>>>%d %d %d\n",len,dp[len][p1],pre[len][p1]); if (dp[len][p1] != 1) printf("no\n"); else { ans.clear(); for (i = len; i >= 1; --i) { if (pre[i][p1] == 0) { // printf("0*********\n"); for (j = 0; j < ivc[i][0].size(); ++j) ans.push_back(ivc[i][0][j]); p1 -= a[i][0]; } else if (pre[i][p1] == 1) { // printf("1*********\n"); for (j = 0; j < ivc[i][1].size(); ++j) ans.push_back(ivc[i][1][j]); p1 -= a[i][1]; } } sort(ans.begin(),ans.end()); vector<int>::iterator it; for (it = ans.begin(); it != ans.end(); ++it) printf("%d\n",*it); printf("end\n"); } } return 0; }
pku 2912 Rochambeau
http://poj.org/problem?id=2912
题意:
n个人分成三组,玩石头剪子布游戏,同一组的人只能出同样固定的的手势,其中有一个是裁判不属于任何组,可以出任意手势,给出m个信息x op y 表示x,y是从三个组里面随机抽取的或者是裁判,他们之间的输赢关系。让你判断最少在第几组信息时,可以唯一判断出裁判,并将裁判号,以及在第几组后判断出来的输出。
思路:
注意这里是能够唯一确定,也就是存在确定的唯一一个裁判。那么我们可以从n个人里面枚举裁判,然后判断除去裁判之后是否还存在矛盾的关系(存在矛盾肯定是裁判在其中导致的),如果存在那么排除该人,记录在第几个信息出现的。枚举完后,如果只存在一个矛盾的人那么这个人就是裁判,如果不存在矛盾,输出Impossible,否则就表示存在多个裁判,输出Can not determine 这里存在矛盾的判断就是用分类并查集处理的了。
 View Code
View Code
#include <iostream> #include <cstdio> #include <cmath> #include <vector> #include <cstring> #include <algorithm> #include <string> #include <set> #include <functional> #include <numeric> #include <sstream> #include <stack> #include <map> #include <queue> #define CL(arr, val) memset(arr, val, sizeof(arr)) #define ll __int64 #define inf 0x7f7f7f7f #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define L(x) (x) << 1 #define R(x) (x) << 1 | 1 #define MID(l, r) (l + r) >> 1 #define Min(x, y) (x) < (y) ? (x) : (y) #define Max(x, y) (x) < (y) ? (y) : (x) #define E(x) (1 << (x)) #define iabs(x) (x) < 0 ? -(x) : (x) #define OUT(x) printf("%I64d\n", x) #define lowbit(x) (x)&(-x) #define Read() freopen("din.txt", "r", stdin) #define Write() freopen("dout.txt", "w", stdout); #define N 502 #define M 2007 using namespace std; struct node { int x,y; char op; }nd[M]; int n,m; int f[N],dep[N]; int err[N]; void init(int len) { for (int i = 0; i <= len; ++i) { f[i] = i; dep[i] = 0; } } int find(int x) { int fa = 0; if (f[x] != x) { fa = f[x]; f[x] = find(f[x]); dep[x] = (dep[x] + dep[fa])%3; } return f[x]; } int main() { // Read(); int i,j; while (~scanf("%d%d",&n,&m)) { for (i = 0; i < m; ++i) scanf("%d%c%d",&nd[i].x,&nd[i].op,&nd[i].y); CL(err,0);//记录当i为裁判时出现矛盾在第几个信息处 for (i = 0; i < n; ++i) { init(n); for (j = 0; j < m; ++j) { if (nd[j].x == i || nd[j].y == i) continue; int tx = find(nd[j].x); int ty = find(nd[j].y); if (tx == ty) { if (nd[j].op == '=' && (dep[nd[j].x] - dep[nd[j].y])%3 != 0) { err[i] = j + 1; break; } else if (nd[j].op == '<' && (dep[nd[j].x] - dep[nd[j].y])%3 != 1 && (dep[nd[j].y] - dep[nd[j].x])%3 != 2) { err[i] = j + 1; break; } else if (nd[j].op == '>' && (dep[nd[j].y] - dep[nd[j].x])%3 != 1 && (dep[nd[j].x] - dep[nd[j].y])%3 != 2) { err[i] = j + 1; break; } } else { if (nd[j].op == '=') { f[tx] = ty; dep[tx] = (dep[nd[j].y] + 0 - dep[nd[j].x])%3; } else if (nd[j].op == '<') { f[tx] = ty; dep[tx] = (dep[nd[j].y] + 1 - dep[nd[j].x])%3; } else { f[ty] = tx; dep[ty] = (dep[nd[j].x] + 1 - dep[nd[j].y])%3; } } } } int k = 0, ans = 0; int ct = 0; for (i = 0; i < n; ++i) { if (err[i] == 0) { k = i; ct++; } if (err[i] > ans) ans = err[i]; } if (ct == 0) printf("Impossible\n"); else if (ct == 1) printf("Player %d can be determined to be the judge after %d lines\n",k,ans); else printf("Can not determine\n"); } return 0; }
扩展的并查集:
pku 1611 The Suspects
http://poj.org/problem?id=1611
记录集合数目:
 View Code
View Code
#include <iostream> #include <cstdio> #include <cstring> #define maxn 30007 using namespace std; int f[maxn],num[maxn]; int n,m,k; void init() { for (int i = 0; i < maxn; ++i) { f[i] = i; num[i] = 1; } } int find(int x) { if (x != f[x]) f[x] = find(f[x]); return f[x]; } void Union(int x,int y) { int tx = find(x); int ty = find(y); if (tx != ty) { f[tx] = ty; num[ty] += num[tx]; } } int main() { int i,j,a,b; while (~scanf("%d%d",&n,&m)) { if (!n && !m) break; init(); for (i = 0; i < m; ++i) { scanf("%d",&k); if (k) scanf("%d",&a); for (j = 1; j < k; ++j) { scanf("%d",&b); Union(a,b); } } int pos = find(0); printf("%d\n",num[pos]); } return 0; }
pku 1988
http://poj.org/problem?id=1988
题意:
有n个栈,每个栈里面放着一个有标号的立方体。对其进行如下操作:
M:x,y 表示把含有标号x的栈放到含有标号y的栈里面;
C:x 表示计算在标号x下边的立方体的个数;
思路:
并查集表示累在一起的立方体的集合,记录每个根节点所有子节点的个数all[i]表示i节点下边一共有多少个立方体。然后用up记录每一个节点的上边节点的个数,最后求的是:
all[root[i]] - up[i]- 1
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
#include <cstring>
#include <algorithm>
#include <string>
#include <set>
#include <functional>
#include <numeric>
#include <sstream>
#include <stack>
#include <map>
#include <queue>
#define CL(arr, val) memset(arr, val, sizeof(arr))
#define lc l,m,rt<<1
#define rc m + 1,r,rt<<1|1
#define pi acos(-1.0)
#define ll long long
#define L(x) (x) << 1
#define R(x) (x) << 1 | 1
#define MID(l, r) (l + r) >> 1
#define Min(x, y) (x) < (y) ? (x) : (y)
#define Max(x, y) (x) < (y) ? (y) : (x)
#define E(x) (1 << (x))
#define iabs(x) (x) < 0 ? -(x) : (x)
#define OUT(x) printf("%I64d\n", x)
#define lowbit(x) (x)&(-x)
#define Read() freopen("din.txt", "r", stdin)
#define Write() freopen("dout.txt", "w", stdout);
#define M 500007
#define N 30007
using namespace std;
int f[N],up[N],all[N];
int n;
void init()
{
int i;
for (i = 0; i < N; ++i)
{
f[i] = i;
up[i] = 0;
all[i] = 1;
}
}
int find(int x)
{
int fa = 0;
if (f[x] != x)
{
fa = f[x];
f[x] = find(f[x]);
up[x] += up[fa];//类似于分类并查集的递归更新
}
return f[x];
}
void Union(int x,int y)
{
int tx = find(x);
int ty = find(y);
if (tx != ty)
{
f[ty] = tx;
up[ty] = all[tx];
all[tx] += all[ty];
}
}
int main()
{
int i,x,y;
char op[2];
while (~scanf("%d",&n))
{
init();
for (i = 0; i < n; ++i)
{
scanf("%s%d",op,&x);
if (op[0] == 'M')
{
scanf("%d",&y);
Union(x,y);
}
else
{
int root = find(x);
printf("%d\n",all[root] - up[x] - 1);
}
}
}
return 0;
}
pku http://poj.org/problem?id=1456
详解见:http://www.cnblogs.com/E-star/archive/2013/03/04/2943268.html
zoj 3261 Connections in Galaxy War
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=3563
题意:
给定n个银河里的行星,以及每个行星的能量值,给出m个边x,y表示行星x与y可以互达。 给出Q个操作,有两种操作destroy a,b,表示把a与b的边毁掉,query a 表示a行星要向其他与他相连的可达的行星求救,如果可以输出该行星的编号,否则输出-1 . 可求救的行星需要满足他的能量值比a大,并且可以a互通。 如果存在最大值一样的输出编号最小的。
思路:
逆序合并,首先离线保存所有输入,然后把所有不被毁坏的边用并查集合并点,倒着处理,当遇到destroy是然后再合并a,b 。并查集的根节点存放该集合里val值得最大的,然后只要该集合的点询问时询问根节点就行。
ps:注意:当遇到query时,我们可能会遇到询问某个集合的节点a(非根节点)是得到的根节点b 他们之间的val值相同,这样的情况是不能寻求帮助的输出-1;
 View Code
View Code
#include <iostream> #include <cstdio> #include <cmath> #include <vector> #include <cstring> #include <algorithm> #include <string> #include <set> #include <functional> #include <numeric> #include <sstream> #include <stack> #include <map> #include <queue> #define CL(arr, val) memset(arr, val, sizeof(arr)) #define ll long long #define inf 0x7f7f7f7f #define lc l,m,rt<<1 #define rc m + 1,r,rt<<1|1 #define pi acos(-1.0) #define L(x) (x) << 1 #define R(x) (x) << 1 | 1 #define MID(l, r) (l + r) >> 1 #define Min(x, y) (x) < (y) ? (x) : (y) #define Max(x, y) (x) < (y) ? (y) : (x) #define E(x) (1 << (x)) #define iabs(x) (x) < 0 ? -(x) : (x) #define OUT(x) printf("%I64d\n", x) #define lowbit(x) (x)&(-x) #define Read() freopen("din.txt", "r", stdin) #define Write() freopen("dout.txt", "w", stdout); #define N 10007 #define M 20007 #define Q 50007 using namespace std; int f[N]; int val[N]; vector<int>ivc[N]; int a[Q],b[Q]; int ans[M]; int n,m,q; void init(int len) { for (int i = 0; i <= len; ++i) f[i] = i; } int find(int x) { if (f[x] != x) f[x] = find(f[x]); return f[x]; } void Union(int x,int y) { int tx = find(x); int ty = find(y); if (tx != ty) { if (val[tx] < val[ty]) f[tx] = ty; else if (val[tx] > val[ty]) f[ty] = tx; else { if (tx < ty) f[ty] = tx; else f[tx] = ty; } } } int main() { // Read(); int i; int x,y; vector<int>::iterator it; int cas = 0; while (~scanf("%d",&n)) { if (cas == 1) printf("\n"); for (i = 0; i < n; ++i) scanf("%d",&val[i]); scanf("%d",&m); for (i = 0; i < n; ++i) ivc[i].clear(); for (i = 0; i < m; ++i) { scanf("%d%d",&x,&y); if (x > y) swap(x,y); ivc[x].push_back(y); } char op[10]; scanf("%d",&q); for (i = 0; i < q; ++i) { scanf("%s",op); if (op[0] == 'q') { scanf("%d",&a[i]); b[i] = -1; } else { scanf("%d%d",&a[i],&b[i]); if (a[i] > b[i]) swap(a[i],b[i]); for (it = ivc[a[i]].begin(); it != ivc[a[i]].end(); ++it) { if (*it == b[i])//把要删除的点处理掉 { *it = -1; } } } } init(n); for (i = 0; i < n; ++i) { for (it = ivc[i].begin(); it != ivc[i].end(); ++it) { if (*it != -1) Union(i,*it); } } int len = 0; for (i = q - 1; i >= 0; --i) { if (b[i] == -1) { int fa = find(a[i]); if (val[fa] != val[a[i]])//注意这里一定要判断似val不能判断fa != a[i] { ans[len++] = fa; } else { ans[len++] = -1; } } else { Union(a[i],b[i]); } } for (i = len - 1; i >= 0; --i) printf("%d\n",ans[i]); cas = 1; } return 0; }
