数据结构入门(5)——树与二叉树的应用
数据结构入门——树与二叉树的应用
文章目录
- 数据结构入门——树与二叉树的应用
- 前言
- 一、压缩与哈夫曼树
-
- 扩充二叉树
- 哈夫曼算法
-
- 哈夫曼算法基本思想
- 哈夫曼算法
- 哈夫曼编码
- 二、表达式树
-
- 如何构造表达式二叉树
- 计算表达式二叉树对应的值
- 三、并查集
-
- 并查集的实现
- 四、初探线段树与树状数组
-
- 线段树
-
- 线段树操作
- 树状数组
-
- 定义
- 操作
- 树状数组和线段树
前言
本系列文章将简要介绍数据结构课程入门知识,文章将结合我们学校(吉大)数据结构课程内容进行讲述。文中算法大部分来自朱允刚老师上课的讲解,朱老师是我遇到最认真负责的老师,很有幸能成为朱老师的学生。
本节较为重要就没有将其合并到树和二叉树中。
一、压缩与哈夫曼树
数据压缩
➢ 数据压缩是计算机科学中的重要技术。
➢ 数据压缩过程称为编码,即将文件中的每个字符均转换为一个唯一的二进制位串。
➢ 数据解压过程称为解码,即将二进制位串转换为对应的字符。
压缩的关键在于编码的方法,哈夫曼编码是一种最常用无损压缩编码方法。
文件压缩策略采用不等长二进制码,要求:
- 文件中出现频率高的字符的编码尽可能短
- 解码过程没有多义性
前缀码:字符集中任何字符的编码都不是其它字符的编码的前缀,满足这个条件的编码被称为前缀码
问题:怎样的前缀码才能使文件的总编码长度最短?
设组成文件的字符集A={a1,a2,…,an},其中,ai的编码长度为li;ai出现的次数为ci 。
设计一个前缀码方案,最小化文件的总编码长度:
m i n ∑ i = 1 n c i l i min \sum_{i=1}^n c_il_i mini=1∑ncili
解决方法:1952年,哈夫曼(Huffman)算法被提出。
扩充二叉树
在开始介绍哈夫曼算法之前,我们先了解一下扩充二叉树
定义
在二叉树中出现空子树的每个地方,都增加特殊的结点(空叶结点),使图(a)变成图(b),由此生成的二叉树(图(b))被称为扩充二叉树。

- 扩充二叉树每一个圆形结点都有两个子结点,每一个方形结点没有子结点。
- 规定空二叉树的扩充二叉树是只有一个方形结点。
- 称圆形结点为内结点,方形结点为外结点。
内部路径长度定义为从根到每个内结点的路径长度之和。
外部路径长度定义为从根到每个外结点的路径长度之和。
扩充二叉树的n个外结点各赋一个实数,称为该结点的权。
树的加权外部路径长度定义为WPL:
W P L = ∑ i = 1 n w i L i WPL=\sum_{i=1}^nw_iL_i WPL=i=1∑nwiLi
其中, n表示外结点的个数,wi和Li分别表示外结点ki的权值和深度。
哈夫曼算法
- n个带权外结点构成的所有扩充二叉树中,WPL值最小者称为最优二叉树 。
- 文件编码问题可以建模为构造扩充二叉树的问题,每个外结点代表一个字符,其权值代表该字符的频率,外结点的深度就是该字符的编码长度。
- 文件的总编码长度即为该二叉树的WPL值。
为求得最优二叉树,哈夫曼巧妙的设计了哈夫曼算法,通过哈夫曼算法可以建立一棵哈夫曼树,进而为压缩文本文件建立哈夫曼编码。
哈夫曼算法基本思想
-
根据给定的n个权值w1, w2, … ,wn构成n棵二叉树的森林F={T1,T2, …,Tn},其中每棵二叉树Ti都只有一个权值为wi的根结点,其左、右子树均空;
-
在森林F中选出权值最小的两个根结点合并成一棵二叉树:生成一个新结点作为这两个结点的父结点,新结点的权值为其两个子结点的权值之和;现在森林中减少了一棵二叉树。
-
重复第②步,直到F中只含有一棵二叉树为止,此树便是哈夫曼树。
哈夫曼算法
假设给定n个实数(权值)所在结点的地址存于一维数组H[1:n]中,该数组按每个结点的Weight域已经排序,即Weight(H[1])≤ … ≤Weight(H[n])
算法思想:
预处理:对H数组排序
每次取出权值最小的两个结点
将合并得到的新子树插入H数组,并保持有序
哈夫曼树中每个结点的结构为:
template <class T>
class node{
public:
T Info;//信息域
int Weight;//权值
node*Llink;//链接域
node*Rlink;
};
//这里的代码仅仅是为了更好的展示算法思想,并不一定可以直接成功运行
void Huffman(node* H[],int n){//这里H数组已经按权值递增排好序
for(int i=0;i<n;++i)
H[i]->Llink=H[i]->Rlink=NULL;
for(int i=0;i<n-1;++i){
node* t=new node;
t->Weight=H[i]->Weight+H[i+1]->Weight;
t->Llink=H[i];
t->Rlink=H[i+1];
//将新结点的地址t插入H中
int j=i+2;
while(j<=n && H[j]->Weight < t->Weight){
H[j-1]=H[j];
++j;
}
H[j-1]=t;
}
}
哈夫曼编码
- 编码过程:依次将数据文件中的字符按哈夫曼树转换成哈夫曼编码。
- 依次将数据文件中的字符按哈夫曼树转换成哈夫曼编码。
- 将哈夫曼树每个分支结点的左分支标上0,右分支标上1,把从根结点到每个叶结点的路径上的标号连接起来,作为该叶结点所代表的字符的编码,这样得到的编码称为哈夫曼编码。
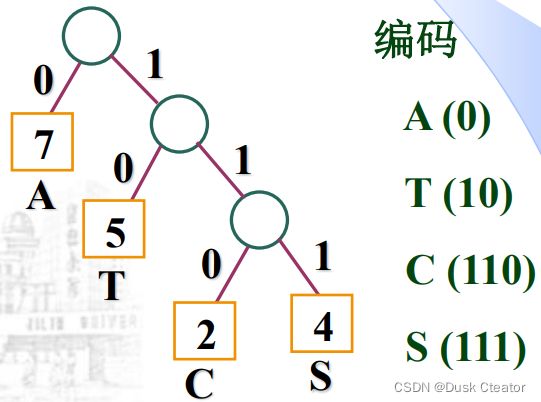
哈夫曼编码是否是前缀码?
字符对应叶结点,每个叶结点对应的编码不可能是其他叶结点对应的编码的前缀,故哈夫曼编码是前缀码。
哈夫曼编码是否唯一?
- 哈夫曼树形态不唯一,编码不唯一,但最小编码长度唯一。
- 如规定根结点权值小的为左子树,若两个根结点权值相等…?
哈夫曼树不包含度为1的结点。哈夫曼树外结点个数为n,则内结点个数为n-1,总结点个数为2n-1。
解码过程:依次读入文件的二进制码,从哈夫曼树的根结点出发,若当前读入0,则走向其左孩子,否则走向其右孩子,到达某一叶结点时,便可以译出相应的字符。
二、表达式树
如何构造表达式二叉树
根据后缀表达式构造表达式二叉树(仅考虑二元运算)
从左向右扫描后缀表达式中符号,建立二叉树:
- 如果是操作数,则生成一个新结点,以此操作数作为该结点的数据域,将此结点作为一棵二叉树压入堆栈中。
- 如果是运算符,则生成一个新结点p,并以此运算符作为该结点的数据域,从栈顶弹出两个结点,作为 p 的左、右孩子,将新结点p压入堆栈中。
- 按照上述方法处理完表达式中所有符号后,堆栈中仅包含一个结点,即所求二叉树的根结点。
计算表达式二叉树对应的值
通过后根遍历一个表达式对应的二叉树,可以计算表达式的值:
- 计算左子树对应表达式的值result1;
- 计算右子树对应表达式的值result2;
- 结合根结点对应的运算符、result1、result2计算整个表达式的值
三、并查集
一些应用问题涉及将n个不同的元素分成一组不相交的集合。
经常需要进行两种操作:①查询某个元素所属的集合, ②合并两个集合。
将维护该不相交集合的数据结构称为并查集。
选择集合中的某个元素代表整个集合,称为集合的代表元。
设x、y表示集合中的元素,并查集的三个操作。
- MAKE_SET(x):建立一个新的集合,它的唯一元素是x,因而x是代表元。
- UNION(x, y):将元素x和y所在的集合合并成一个集合。
- FIND(x):找x所在的集合,返回该集合的代表元。
并查集的实现
- ➢ 并查集的一种高效实现方式是使用树表示集合。
- ➢ 每棵树代表一个集合。
- ➢ 树的每个结点表示集合的一个元素,根结点表示集合的代表元。
设x、y表示集合中的元素,并查集的三个操作。
- ➢ MAKE_SET(x):建立一个新的集合,它的唯一元素是x,因而x是代表元。为元素x生成一棵单结点树,x的父结点是特殊值或自己。
- ➢ FIND(x):返回x所在集合的代表元,查找元素x所在的树的根结点。
- ➢ UNION(x, y):将x和y所在的集合合并成一个集合。合并x所在的树和y所在的树,让一棵树的根结点的父指针指向另一棵树的根结点。
并查集的这种实现方式只需要树的向上访问能力,只需存储每个结点的父结点信息。故可采取Father数组的方法。

void Make_Set(int x){
// 实现并查集的MAKE_SET操作,为元素x生成一棵单结点树
Father[x]=0;
}
int Find(int x){
// 实现并查集的FIND操作,查找x所在树的根结点
if(Father[x]==0)return x;
else return Find(Father[x]);
}
void Union(int x,int y){
// 实现并查集的UNION操作,合并x和y的树,y所在树的根结点指向x所在树根结点
Father[Find(y)]=Find[x];
}
四、初探线段树与树状数组
线段树
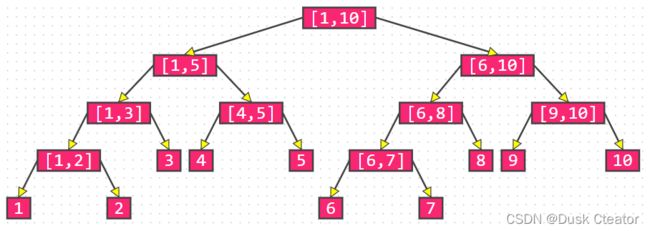
- 一棵二叉树,每个结点对应一个区间[L, R]。
- 根结点代表整个统计范围[1,n]。
- 每个叶结点代表一个长度为1的区间[x, x]。
- 对于每个非叶结点所表示的区间[L, R],其左孩子表示的区间为[L, mid],右孩子表示的区间为[mid+1, R],其中mid =(L+R)/2。
特点:
- 同一层结点所代表的区间,相互不会重叠。
- 除最下一层外,同一层结点所代表的区间加起来是连续的区间。
- 除了最后一层,其他层构成一棵满二叉树
- 若根结点对应的区间是[1,n],则树高 ⌈ l o g n ⌉ \lceil{logn}\rceil ⌈logn⌉
- 叶结点的数目和根结点表示的区间长度相同。
- 结点度0或2,叶结点n个,总结点2n-1个。
- 结点内可维护区间的信息,如和、最值等。
- 可使用顺序存储方式,数组开4n大小。
线段树操作
struct Node{
int L,R;
int sum;
};
Node tree[N*4];
//建树
void build(int root, int L, int R){
tree[root].L = L;
tree[root].R = R;
if (L == R) { //叶结点,区间长度为1
tree[root].sum = a[L];
return;
}
int mid = (L + R)/2;
build(2*root, L, mid);
build(2*root+1, mid+1, R);
tree[root].sum=
tree[2*root].sum+tree[2*root+1].sum;
}
//单点更新
void update(int root, int i, int x){ //a[i]加上x
if (tree[root].L==tree[root].R){
tree[root].sum += x;
return;
}
int mid=(tree[root].L+tree[root].R)/2;
if (i<=mid) update(2*root, i, x);
else update(2*root+1, i, x);
tree[root].sum=tree[2*root].sum+tree[2*root+1].sum;
}
//区间查询
int query(int root, int L, int R){
if (L==tree[root].L && R==tree[root].R)
return tree[root].sum;
int mid=(tree[root].L+tree[root].R)/2;
if (R<=mid)
return query(2*root, L, R);
else if (L>mid)
return query(2*root+1, L, R);
else
return query(2*root, L, mid)+query(2*root+1, mid+1, R);
}
树状数组
定义
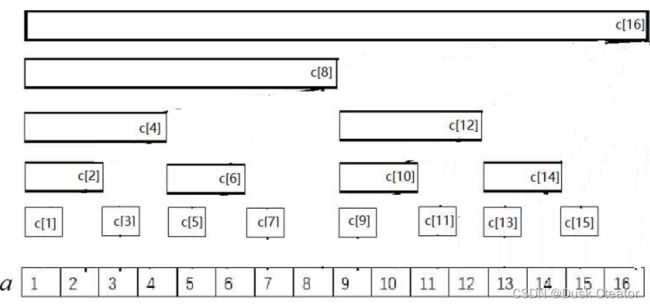
- 对于数组a,我们设一个数组c
- 运算 lowbit(x) = x & (-x) (x的二进制表示形式留下最右边的1,其他位都变成0)
- c[i]=a[i-lowbit(i)+1]+a[i-lowbit(i)+2]+…+a[i]
- c即为a的树状数组(i从1开始算,c[0]和a[0]没用)
c[i]=a[i-lowbit(i)+1]+a[i-lowbit(i)+2]+…+a[i]
C[1]=A[1]
C[2]=A[1]+A[2]
C[3]=A[3]
C[4]=A[1]+A[2]+A[3]+A[4]
C[5]=A[5]
C[6]=A[5]+A[6]
C[7]=A[7]
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]
…………
C[16]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8]+A[9]+A[10]+A[11]+A[12]+A[13]+A[14]+A[15]+A[16]
操作
x的二进制表示形式留下最右边的1,其他位都变成0
int lowbit(int x) {
return x & -x;
}
(1)区间查询
查询a[1]+…+a[i]:从c[i]开始沿父结点往上走,将沿途结点累加,即将c[i]及其祖先结点相加。
int query(int i) { //查询a[1]+…+a[i]
for (int sum=0; i>0; i-=lowbit(i))
sum+=c[i];
return sum;
}
(2)单点更新
更新a[i] :从c[i]开始沿父结点往上走,将沿途结点更新,即将c[i]及其祖先结点更新。
void update(int i, int x) { //a[i]+=x
for(; i<=n; i+=lowbit(i))
c[i]+=x;
}
(3)构建树状数组
c[i]=a[i-lowbit(i)+1]+a[i-lowbit(i)+2]+…+a[i]
void build(int a[], int n){
sum[0]=0;
for(int i=1; i<=n; i++){
sum[i]=sum[i-1]+a[i];
c[i]=sum[i]-sum[i-lowbit(i)];
}
}
树状数组和线段树
- 树状数组能解决的问题线段树都能解决,线段树能解决的问题树状数组未必能解决。
- 线段树和树状数组时间复杂度相同,但树状数组的常数更低些,且空间消耗更少,代码简单。
- 如果一个问题既能用树状数组也能用线段树解决,首选树状数组。
- 单点更新区间求和,树状数组更快