数据探索性分析的基础介绍
数据探索性分析的基础介绍
导读:当我们拿到数据之后,总是会因某些原因,加速对数据的使用,希望能够快速的产出成果,待回头检查发现,对数据情况的不尽了解,将有可能违背预测模型的一些重要的统计假设,比如要求变量的正态分布,方差齐性,不相关等等,做出来的模型效果也可能因此产生错误的“好”或者错误的“坏”,耗费额外的模型开发成本,导致项目风险的增加。为避免上述事情发生,需要在对数据加工之前进行探索性分析,以此了解数据的特征,做到合理的使用数据。
探索性数据分析(Exploratory Data Analysis,EDA)是指对已有数据在尽量少的先验假设下通过作图、制表、方程拟合、计算特征量等手段探索数据的结构和规律的一种数据分析方法。常用的手段包括定量分析和可视化技术。
本章具体内容:
-
常用统计指标及代码示例
-
可视化及代码示例
为了更好的说明,本次我们使用Seaborn库自带的一场马拉松比赛数据进行相关演示。
为了能使用Seaborn 画图,将原始数据读入并处理
def convert_time(s):h,m,s = map(int,s.split(':'))return int(h)*3600+int(m)*60+int(s)*1
#读入marathon-data数据with open('marathon-data.csv') as f:data = pd.read_csv(f,converters={'final':convert_time,'split':convert_time})data.shape
Out[1] (37250, 4)
1. 常用统计指标
1.1 单一变量的统计量估计
频数、缺失值、最大值、最小值、中位数、众数、均值、25分位数、75分位数、偏度、峰度、方差、标准差。
对上述统计量的结果进行观察和分析后,我们才能够更好的使用数据。
查看样本
data.head()data.info();缺失值及变量类型&样本概述
data.describe()分位数也可以这么获取,可以灵活的查取想要的分位点
age = data['age']q1 = np.quantile(age,0.25)q1
Out[3]:33.0
或者根据自己的需要,定义其他功能函数,如下示例
#根据设置分箱统计各分位点
def pctnum(value,cuts = 10,digt = 4):'''value:待分析数据cuts:分位点数digt:保留的小数位数'''value = pd.Series(value)na_rate = round(value.isnull().sum()/len(value),digt)result = pd.DataFrame({'na_rate':na_rate},index = [''])for n in range(cuts+1):cut_point = (1/cuts) * ncut_value = np.percentile(value[value.notnull()],cut_point*100)result_temp = pd.DataFrame({"%.2f%%" % (cut_point * 100):round(cut_value,digt)},index = [''])result = pd.concat([result,result_temp],axis = 1)return result
描述数据离散度的方差和标准差
std_age = age.var()var_age = age.var()std_agevar_age
1.2 多变量的统计
相关性
相关关系,是指2个或2个以上变量取值之间在某种意义下所存在的规律,其目的在于探寻数据集里所隐藏的相关关系网。
data.corr()2. 可视化
上例age与age的相关性,当然是1。一般我们在使用数据时要求A变量与B变量之间的相关性最好低于0.7,甚至更低一些,如0.6。
人类从外界获取的信息83%来自视觉,11%来自听觉。善于利用图形进行数据信息的传递对我们的工作效率将是极大的提升。
Matplotlib已经证明了自己是一款超级实用且流行的数据可视化工具,但仍然不得不承认它不支持的功能还有很多。“罪状”主要总结如下:
-
Matplotlib 2.0 之前的版本的默认配置样式仍然仿照1999年MATLAB,却一直在使用。
-
Matplotlib的API比较底层。虽然可以实现复杂的统计数据可视化,但通常都需要写大量的样板代码。
-
Matplotlib比Pandas早十几年,因此它并不是为了Pandas的DataFrame设计的。为了实现Pandas的DataFrame数据的可视化,你必须先提取每个Series。
Seaborn其实是在matplotlib的基础上进行了更高级的API封装,从而使得作图更加容易,在大多数情况下使用seaborn就能做出很具有吸引力的图,为数据分析提供了很大的便利性。
现在可以通过jointplot函数画图,从而对数据有个认识
with sns.axes_style('white'):g = sns.jointplot("split","final",data,kind="hex")g.ax_joint.plot(np.linspace(4000,16000),np.linspace(8000,32000),':k')图中的实线点表示一个人全程匀速跑完马拉松,然而从图中我们发现,绝大多数人都是越跑越慢(也符合常理)。
创建一列(split_frac,split fraction)来表示前后半程的差异,衡量比赛选手前后加速的程度:
data['split_frac'] = 1-2*data['split']/data['final']data.head()
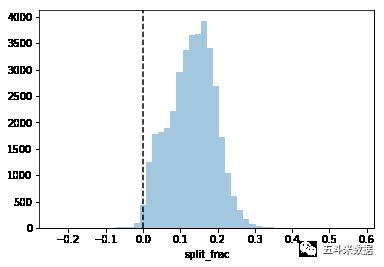
sns.distplot(data['split_frac'],kde=False);如果前后半程差异系数小于0,就表示这个人是后半程加速选手。让我们画出差异系数的分布图
plt.axvline(0,color="k",linestyle="--");sum(data.split_frac<0)Out[3]:251
在大约4万名选手中,只有约250人能做到后半程加速。
再看看前后半程差异系数与其他变量是否有相关性,用一个矩阵图pairgrid画出所有变量的相关性。
g = sns.PairGrid(data,vars=['age','split','final','split_frac'],hue='gender',palette='RdBu_r')g.map(plt.scatter,alpha=0.8)g.add_legend()
从图中可以看出,虽然前后半程差异系数与年龄没有显著相关性,但与比赛的最终成绩有显著的相关性:冠军选手的前后半程速度尽量保持一致。
对比男女选手间的差异同样是一件有趣的事情。看一下两组选手的前后半程差异系数的频次直方图。
sns.kdeplot(data.split_frac[data.gender=='M'],label='men',shade=True)sns.kdeplot(data.split_frac[data.gender=='W'],label='women',shade=True)plt.xlabel('split_frac')
有趣的事,在前后半程耗时接近的选手中,男选手的比例要大于女选手。
3 小结
数据探索性分析能快速描述一份数据集,为清洗数据方法提供可靠的依据,可视化数据分布能直观的感知数据特征。
——