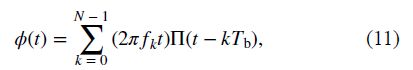基于cnn的短文本分类_基于时频分布和CNN的信号调制识别分类方法
文章来源:IET Radar, Sonar & Navigation, 2018, Vol. 12, Iss. 2, pp. 244-249.
作者:Juan Zhang1, Yong Li2, Junping Yin3
作者单位:
1. School of Mathematical Sciences, Beijing Normal University, No.19, XinJieKouWai Street, HaiDian District, Beijing, People's Republic of China
2. School of Statistics, Bejing Normal University, No.19, XinJieKouWai Street, HaiDian District, Beijing, People's Republic of China
3. Institute of Applied Physics and Computational Mathematics, No.6, Hua Yuan Street, HaiDian District, Beijing, People's Republic of China
摘要:
信号调制分类是军事和民用领域的重要研究课题。该研究提出了一种基于时频分布和卷积神经网络的调制分类新方法。仿真结果表明,本研究提出的方法高效,并且具有较强的鲁棒性,能够高度自动化地提取特征,训练权重和制定决策。此外,在小样本反复训练的情况下,本方法相比于其他传统方法具有很好的性能。
1 介绍
自动调制分类是信号检测和解调之间的中间步骤,目的是在几乎不了解先验知识的情况下识别接收信号的调制方式[1]。调制方案识别的方法大致可分为以下两类[2]:基于似然性(LB)和基于特征的方法。大多数LB分类器[3-8]需要对参数进行估计,并且由于积分和指数运算[9]会提高时间的运行成本,所以许多学者想要达到降低计算复杂性[10-12]的目的开始尝试其他方法,其中基于特征的方法没有参数估计[2],并且易于实现[13]。该方法的性能取决于两个因素:正确的特征集和有效的分类方法。迄今为止,已经提出了各种类型的基于光谱分析的特征[14-16],小波变换[17],星座图[18],高阶统计量[19-22]和时频分布[23-25]。但是,研究人员一直在该领域寻找具有更好性能的特征,例如改善的信噪比(SNR)性能和更大的通用性。根据调制识别的数学理论,本文提出了一种新的调制分类方法。通过时频分析,每个信号都在时域和频域中转换为映射,从而充分说明了信号在时间和频率上能量的变化。同时由于卷积神经网络(CNN)作为计算机视觉中特征提取的出色模型,本文将此类信号图视为CNN的输入以提取特征。
2 调频模型
信号的解析模型如下所示:
其中,A(t)表示幅度调制,φ(t)表示相位调制[26],其中包含频率调制(FM)和相位调制。μ(t)表示噪声,其在本文中表示为加性高斯白噪声。本文中研究的调制信号为FM,将幅度A(t)表示为常量A,其瞬时频率由下式给出:
其中fc表示信号的载波频率,Kf表示频率,m(t)是信号的基带信息。
未调制信号(常量)
线性调频信号(LFM)
正弦调频信号(SFM)
多项式调频信号(PFM)
频移键控信号(FSK)
其中k,a1,a2是调制系数,fk是第k个频率编码,II(t)是具有符号周期Tb的矩形窗函数。本文研究的信号是FM信号,LFM信号,非线性调频(SFM和PFM)信号以及具有多个频率分量(FSK)的信号。
3 时频分析
时间和频率是用来描述信号的两个最重要的物理特性,调制特征主要体现在相对于时间的相位变化中。但是,由于FM信号的瞬时相位和瞬时频率之间存在积分关系,因此研究瞬时频率的变化更具指导意义。时频分析得出时间和频率的联合分布,反映了信号能量中时间和频率的变化。此外,从统计角度来看,时频分布包含有关信号的更加完整的信息,是信号分类的有效特征。文献[2]中提出,在认知无线电的调制分类中,基于时间频率的特征比基于累积量的特征表现更好。从20世纪中叶开始,Wigner,Ville,Gabor和Cohen等人就陆续提出了几种组合时间t和频率f的方法。由下面给出的表达式定义的Wigner-Ville分布是时频分析中最重要,使用最广泛的分布:
其中,x*(t)是x(t)的核函数,Wx(t,f)是一个二维函数,能够将其视为信号特征来对信号进行分类。图1显示了时频分布图能够直观地了解调制模式,Wigner-Ville分布只是可用的时频分析方法之一,可以针对任何特定应用选择最佳方法。
4 卷积神经网络
良好的特征选择对于算法的准确性十分重要,本文中要实现的目标是提取最佳特征来表示任何一种调制信号。与传统方法中人为选择的特征不同,本文提取的特征使用特殊的神经网络CNN进行提取,这种方法是直接受到深度学习中逐层提取和抽象特征的启发。CNN旨在处理多种数组形式的数据,并在许多任务中表现出色,例如图像分类和语音识别[27]。如文献[28]所示,CNN的体系结构包含一系列阶段,前几个阶段由卷积层和池化层组成。卷积运算和卷积核在图像处理领域并不是一个新概念,通过调整内核元素的值,能够产生不同的效果[29],例如边缘检测,锐化以及模糊处理,可以利用这些来检测前一层的局部特征并提取不同级别的特征。
合并过程可以将多个语义相似的特征合并为一个模型,从而提高模型的通用性[30]。此外,考虑到像素的空间位置,本文选择CNN来代替深度置信网络,自动编码器以及其他深度学习方法。图2显示了信息是自下向上的,通过使用较低级的特征充当定向的边缘检测器。图2a显示了SNR=4dB的SFM信号的原始波形。为了研究其调制类型,一种常用的方法是通过相位差估算瞬时频率[31]。
从图2c中能够看出,它的瞬时频率趋势不是很明显,并且在较低的SNR情况下会表现得更差。除此之外,过多噪声将对传统分类方法的鲁棒性产生很大影响。因此,本文提出的方法的主要目的是将时频分析和CNN这两个方法有效地结合起来,并整合它们的优势。图2的b, e–h显示了本文仿真生成的SFM信号的整个分类过程。图2的h中的结果表明,通过卷积和池化操作提取的特征能够识别此信号的调制模式。此外,本文将在下一部分中以低SNR测试该算法的鲁棒性。
5 仿真结果
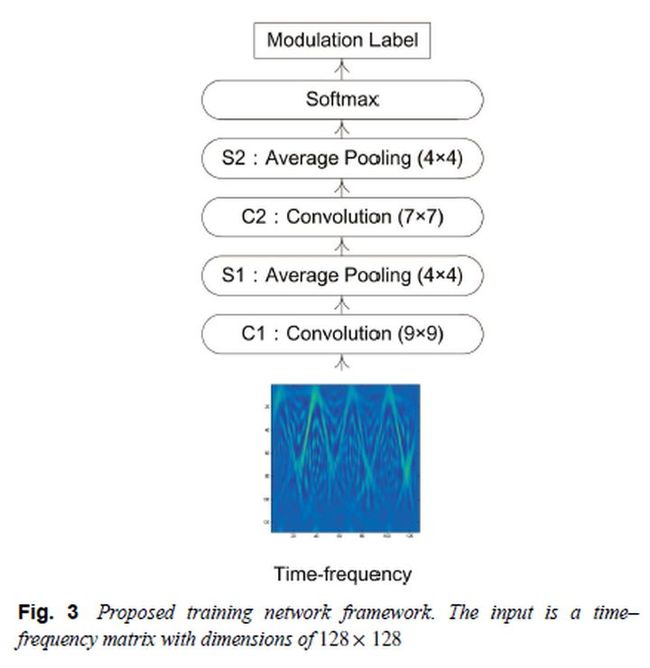
在本节中,将对第2.2节中提到的五种频率调制信号:LFM,SFM,PFM,FSK和Const来进行调制识别,本文中所有信号的数据均使用时频分析工具箱[32]生成。SNR是信号处理领域的关键指标,可以通过算法在低SNR下的识别率,来判别算法是否具有较高的稳定性和可靠性。另外,由于该算法在训练样本不足的情况下表现良好,因此在有限数据的实际应用中将非常有用。本文为了在SNR和小样本情况下测试所提出算法的性能,设计了以下仿真。图3显示了典型CNN模型中的训练过程以及每层滤波器的尺寸。使用Wigner-Ville公式(13)将每个信号转换到时频域。然后,将时频矩阵作为CNN[33]的输入,通过使用反向传播的梯度下降来法训练各层之间的权重。
5.1 不同SNR下的仿真结果
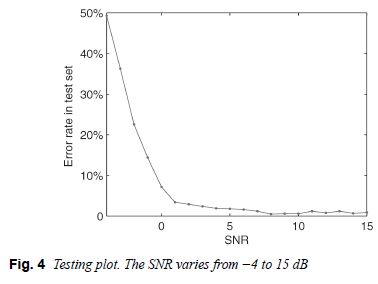
本文生成4000×5信号来训练CNN网络的权重,如图4所示。对于训练集中的每个信号,调制参数都是根据以下两个方法来随机生成的:瞬时频率的范围在[0,0.5]之间,这是为了让时频分布的形状特征得以保持。对于训练集中的每个信号,SNR遵循均匀分布U(–4,15)。除此以外,本文使用一组SNR在-4至15dB之间变化的测试集来测试本文的方法在不同SNR下的性能。测试结果显示在图4中,该图显示了错误率从49.3%(在SNR=–4dB时)急剧下降到7.2%(在SNR =0dB时),然后缓慢下降至1%左右。
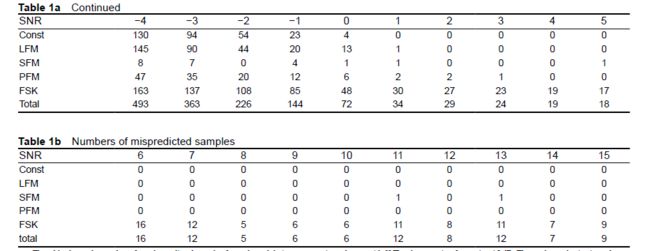
表1显示,随着SNR的提高,每种信号的错误率都呈现下降趋势。在五种调制信号中,FSK测试结果不如其他结果,FSK总是表现出最差的性能,并且当SNR>0dB时,约有100%的样本会被错误地预测。但是,当SNR>3dB时,FSK的精度能够达到90%。同时,对于其他四种类型,当SNR>0dB时,错误率非常接近零。
为了分析实验结果中FSK性能较差的问题,本文分析了FSK及其参数。图5中信号的测试结果为[0.317,0.001,0.000,0.351,0.331]。它们分别对应的是是Const,LFM,SFM,PFM和FSK信号。该算法选择最高的输出作为其调制类型。实验结果表明,FSK与Const和PFM容易混淆。
5.2 小样本属性
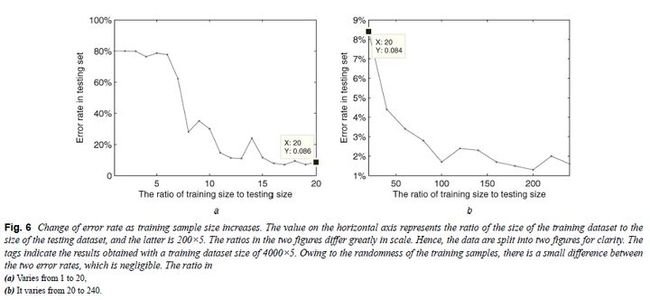
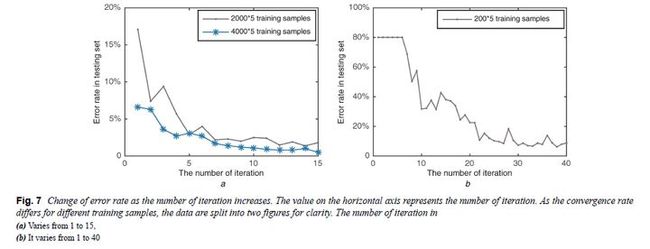
为了研究网络随着训练集中的数据量的增加如何运行,训练集中的样本数量从200×5到4000×5不等,图6a中展示了仿真实验的结果。其中测试集包含200×5个随机SNR的样本。图6显示,错误率随训练样本量的增加而减小,但结果并不是单调的。当SNR约为6时,错误率从大约75%的急剧下降到低于40%,然后结果逐渐稳定在甚至更低的数值,接近2%。图7显示随着迭代次数增加,本文算法的错误率会随着迭代次数的增加而降低。
5.3 仿真结果的比较
根据文献[9]中提供的结果,可以对各种其他方法的性能进行基本了解,例如最大似然(ML)方法,Kolmogorov-Smirnov检验,高阶矩(或累积量)方法,K近邻方法等。文献[9]中的图8.8和图8.15显示了这些方法在SNR和信号长度方面的平均分类精度结果。图8.8中的结果表明,使用ML方法可获得最佳性能,当SNR>4dB时,其精度大于90%。根据图8.15显示,当SNR=10dB且信号长度为128时,与ML方法相比,本文方法在准确性方面显示出更好的性能。
个人总结:
参考文献: