HIT CSAPP LAB6
Cachelab
高速缓冲器模拟
目 录
第1章 实验基本信息 - 3 -
1.1 实验目的 - 3 -
1.2 实验环境与工具 - 3 -
1.2.1 硬件环境 - 3 -
1.2.2 软件环境 - 3 -
1.2.3 开发工具 - 3 -
1.3 实验预习 - 3 -
第2章 实验预习 - 4 -
2.1 画出存储器层级结构,标识容量价格速度等指标变化(5分) - 4 -
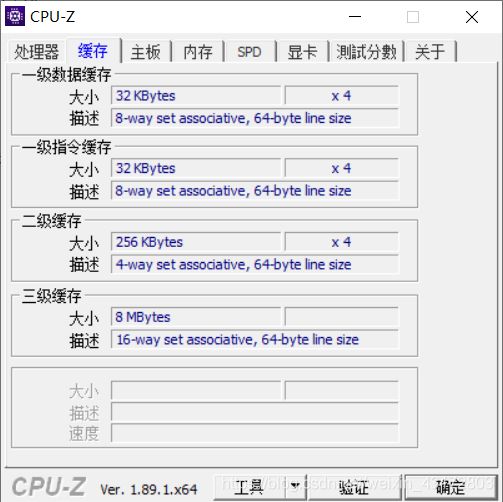
2.2用CPUZ等查看你的计算机CACHE各参数,写出各级CACHE的C S E B S E B(5分) - 4 -
2.3写出各类CACHE的读策略与写策略(5分) - 5 -
2.4 写出用GPROF进行性能分析的方法(5分) - 5 -
2.5写出用VALGRIND进行性能分析的方法((5分) - 6 -
第3章 CACHE模拟与测试 - 8 -
3.1 CACHE模拟器设计 - 8 -
3.2 矩阵转置设计 - 10 -
第4章 总结 - 21 -
4.1 请总结本次实验的收获 - 21 -
4.2 请给出对本次实验内容的建议 - 21 -
参考文献 - 22 -
第1章 实验基本信息
1.1 实验目的
理解现代计算机系统存储器层级结构
掌握Cache的功能结构与访问控制策略
培养Linux下的性能测试方法与技巧
深入理解Cache组成结构对C程序性能的影响
1.2 实验环境与工具
1.2.1 硬件环境
X64 CPU;2GHz;2G RAM;256GHD Disk 以上
1.2.2 软件环境
Windows7 64位以上;VirtualBox/Vmware 11以上;Ubuntu 16.04 LTS 64位/优麒麟 64位;
1.2.3 开发工具
Visual Studio 2010 64位以上;TestStudio;Gprof;Valgrind等
1.3 实验预习
上实验课前,必须认真预习实验指导书(PPT或PDF)
了解实验的目的、实验环境与软硬件工具、实验操作步骤,复习与实验有关的理论知识。画出存储器的层级结构,标识其容量价格速度等指标变化
用CPUZ等查看你的计算机Cache各参数,写出C S E B s e b
写出Cache的基本结构与参数;写出各类Cache的读策略与写策略
掌握Valgrind与Gprof的使用方法
第2章 实验预习
2.1 画出存储器层级结构,标识容量价格速度等指标变化(5分)

从上到下分别为L0 L1 L2 L3 L4 L5 L6
高层的存储器保存着从底层的存储器取出的缓存行
2.2用CPUZ等查看你的计算机Cache各参数,写出各级Cache的C S E B s e b(5分)
| 名称(级别类型) | C | S | E | B | s | e | b |
|---|---|---|---|---|---|---|---|
| 一级数据缓存 | 32KB | 64 | 8 | 64B | 6 | 3 | 6 |
| 一级代码缓存 | 32KB | 64 | 8 | 64B | 6 | 3 | 6 |
| 二级缓存 | 256KB | 1024 | 4 | 64B | 10 | 2 | 6 |
| 三级缓存 | 8MB | 8192 | 16 | 64B | 13 | 4 | 6 |
2.3写出各类Cache的读策略与写策略(5分)
Cache读策略:
1、缓存命中,则从cache中读相应数据到CPU或上一级cache中。
2、缓存不命中,则从主存或下一级cache中读取数据,并替换出一行数据。
Cache写策略:
①.写一个已经缓存了的字w(写命中)是,在高速缓存更新了它的w的副本之后,
1、直写
立即将w的高速缓存块写回到紧接着的低一层中。
2、写回
尽可能的推迟更新,只有当替换算法要驱逐这个更新过的块时,才把它写到紧接着的第一层中。
②.写不命中时,
1、写分配
加载相应的低一层的块到高速缓存中,然后更新这个高速缓存块。
2、非写分配
避开高速缓存,直接把这个字写到低一层中去。
2.4 写出用gprof进行性能分析的方法(5分)
gprof是GNU profile工具,可以运行于linux、AIX、Sun等操作系统进行C、C++、Pascal、Fortran程序的性能分析,用于程序的性能优化以及程序瓶颈问题的查找和解决。通过分析应用程序运行时产生的“flat profile”,可以得到每个函数的调用次数,每个函数消耗的处理器时间,也可以得到函数的“调用关系图”,包括函数调用的层次关系,每个函数调用花费了多少时间。使用步骤如下:
(1)用gcc、g++、xlC编译程序时,使用-pg参数,如:g++ -pg -o test.exe test.cpp编译器会自动在目标代码中插入用于性能测试的代码片断,这些代码在程序运行时采集并记录函数的调用关系和调用次数,并记录函数自身执行时间和被调用函数的执行时间。
(2)执行编译后的可执行程序,如:./test.exe。该步骤运行程序的时间会稍慢于正常编译的可执行程序的运行时间。程序运行结束后,会在程序所在路径下生成一个缺省文件名为gmon.out的文件,这个文件就是记录程序运行的性能、调用关系、调用次数等信息的数据文件。
(3)使用gprof命令来分析记录程序运行信息的gmon.out文件,如:gprof test.exe gmon.out则可以在显示器上看到函数调用相关的统计、分析信息。上述信息也可以采用gprof test.exe gmon.out> gprofresult.txt重定向到文本文件以便于后续分析。
2.5写出用Valgrind进行性能分析的方法(5分)
Valgrind是运行在Linux上一套基于仿真技术的程序调试和分析工具,它包含一个内核──一个软件合成的CPU,和一系列的小工具,每个工具都可以完成一项任务──调试,分析,或测试等。Valgrind可以检测内存泄漏和内存违例,还可以分析cache的使用等。Valgrind包含以下工具:Memcheck(用来检测程序中出现的内存问题,所有对内存的读写都会被检测到,一切对malloc()/free()/new/delete的调用都会被捕获)、Callgrind(收集程序运行时的一些数据,建立函数调用关系图,还可以有选择地进行cache模拟。在运行结束时,它会把分析数据写入一个文件,callgrind_annotate可以把这个文件的内容转化成可读的形式)、Cachegrind(模拟CPU中的一级缓存I1,Dl和二级缓存,能够精确地指出程序中cache的丢失和命中。如果需要,它还能够为我们提供cache丢失次数,内存引用次数,以及每行代码,每个函数,每个模块,整个程序产生的指令数)、Helgrind(用来检查多线程程序中出现的竞争问题)、Massif(堆栈分析器,能测量程序在堆栈中使用了多少内存,告诉我们堆块,堆管理块和栈的大小)。Valgrind的使用非常简单,valgrind命令的格式如下:valgrind [valgrind-options] your-prog [your-prog options] 。一些常用的选项如下:
| 选项 | 作用 |
|---|---|
| -h --help | 显示帮助信息 |
| –version | 显示valgrind内核的版本,每个工具都有各自的版本 |
| -q --quiet | 安静地运行,只打印错误信息 |
| -v --verbose | 打印更详细的信息。 |
| –tool= [default: memcheck] | 最常用的选项。运行valgrind中名为toolname的工具。如果省略工具名,默认运行memcheck。 |
| –db-attach= [default: no] | 绑定到调试器上,便于调试错误。 |
第3章 Cache模拟与测试
3.1 Cache模拟器设计
提交csim.c
程序设计思想:
1.程序定义的cache结构体:
typedef struct cache_line {
char valid;
mem_addr_t tag;
unsigned long long int lru;
} cache_line_t;
typedef cache_line_t* cache_set_t;
typedef cache_set_t* cache_t;
2.程序主要的函数:
在main中从命令行参数读取计算S,E,B. 如下:
S = 1 << s;
B = 1 << b;
E = E;
initCache()函数 - 分配内存,写0表示有效和标记和LRU,为它们初始化
cache = (cache_set_t *)malloc(S * sizeof(cache_set_t));
cache[i] = (cache_line_t *)malloc(E * sizeof(cache_line_t));//为行申请空间
freeCache()函数:为释放空间,根据申请空间的倒序来释放即可。
void replayTrace(char* trace_fn) :此函数基本已经全部给出,主要的就是从trace文件中读取数据,并且调用accessdata函数,操作类型若为 'L’或 ‘S’,则调用一次accessdata,若为 ‘M’ ,则多调用一次accessdata 。 另外在次函数中读取了地址addr之后,可以计算出组索引和标记:
mem_addr_t tag_now = (addr >> b) >> s;
set_index_mask = (addr >> b) & ((1 << s) - 1);
accessData - 访问内存地址addr的数据。
1)如果它已经在cache中,即冲突命中,则hit_count++,lru_counter++
2)如果它不在cache中,将其放入缓存中,miss_counter++。
3)如果一条线被驱逐,则eviction_count++
当组索引找到的某一组,存在一行有效位为1,并且标记匹配时hit发生。
若不命中,则miss_count++。
若组索引找到的某一组,有效位全部为1,此时驱逐某一块发生eviction_counter++ ,并且找到lru最小的那一行,驱逐。
否则只需任意取一块空块将addr信息存入。
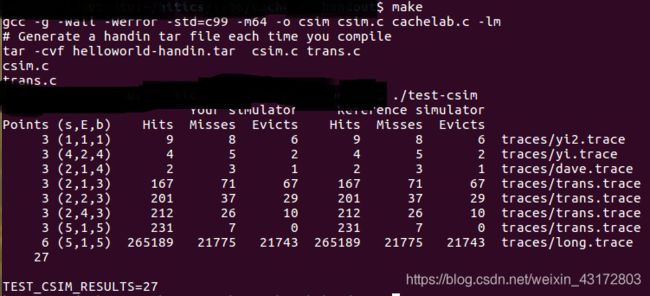
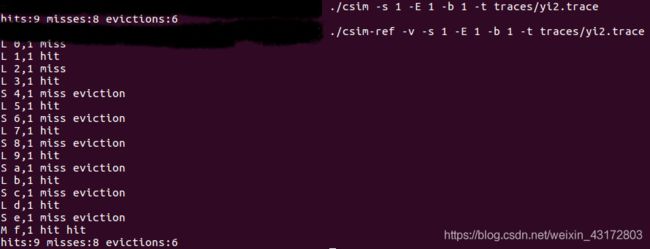
测试用例1的输出截图(5分):
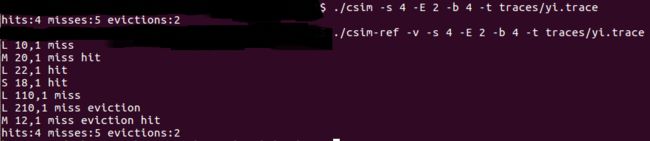
测试用例2的输出截图(5分):
测试用例3的输出截图(5分):

测试用例4的输出截图(5分):
![]()
测试用例5的输出截图(5分):
![]()
测试用例6的输出截图(5分):
![]()
测试用例7的输出截图(5分):
![]()
测试用例8的输出截图(10分):
![]()
注:每个用例的每一指标5分(最后一个用例10)——与参考csim-ref模拟器输出指标相同则判为正确
3.2 矩阵转置设计
提交trans.c
程序设计思想:
由于32 * 32过大,先以4 * 4矩阵进行分析。
将注册的其他函数先注释掉,只保留原始trans函数:

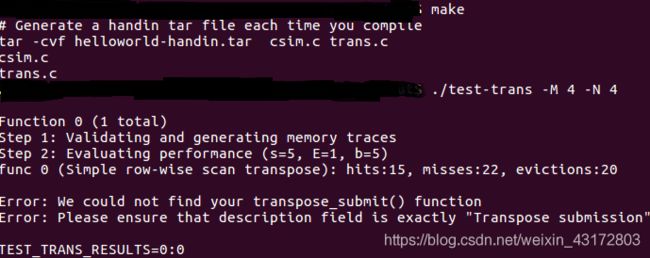

显然,由于cache的块的大小为32个字节,即8个int型数据,故数组中前8个元素会在用一个块中,后8个在另外一个块中,如下图,A按行访问,B按列访问:
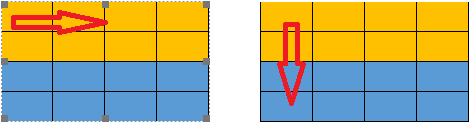
1、A数组访问A[0][0],冲突不命中,将块11装入cache。
2、B数组访问B[0][0],虽然B[0][0]所映射的块11在cache中,但是标记位不同,造成冲突不命中,重新将数组B对应的块11装入cache。
3、A数组访问A[0][1],虽然A[0][1] 所映射的块11在cache中,但是标记位不同,造成冲突不命中,重新将数组A对应的块11装入cache。
4、B数组访问B[1][0],虽然B[1][0]所映射的块11在cache中,但是标记位不同,造成冲突不命中,重新将数组B对应的块11装入cache。
5、A数组访问A[0][2],虽然A[0][2]所映射的块11在cache中,但是标记位不同,造成冲突不命中,重新将数组A对应的块11装入cache。
6、B数组访问B[2][0],B[2][0] 所映射的块12不在cache中,冲突不命中,将数组B对应的块12装入cache。
7、A数组访问A[0][3],A[0][3]所映射的块11在cache中,且标记位相同,故命中。
8、B数组访问B[3][0],B[3][0]所映射的块12在cache中,且标记位相同,故命中。
剩余的操作以同样的方法可以分析得出类似的过程。
由上述分析知,造成冲突不命中的原因是B数组与A数组中下标相同的元素会映射到同一个cache块。
我们可以通过尝试一次性访问同一个块中的多个元素,以减少冲突不命中的数目。
针对32 * 32的矩阵,由于每个块可以存8个int型的数据,cache共有32个块,即32个组,故对于32×32的矩阵而言,每一行的32个元素占4个组,每8行会占满整个cache。
这样32 * 32的矩阵颜色相同的两个块对应关系相同。

首先由于1block存8个数,故先采用用一次访问8个数的方法减少冲突。
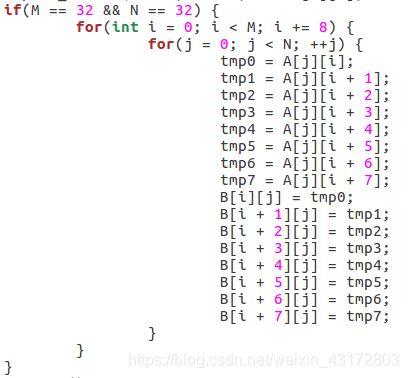
此时,其冲突数目如下:
这样针对32*32的矩阵,A冲突命中与否如下,m表示不命中,h表示命中

B冲突命中与否如下,同样表示方法有:

对于B数组而言,处于对角线上的元素也不命中。这是可以继续优化的部分。
对角线上如第二行的第二列的不命中,由于将A第一行的数据进行转置时会访问到B数组的第二行,而随后A数组也会访问到第二行,接着B又会重新访问第二行,这个第二次访问第二行的过程就是一次冲突不命中。按照这个访问过程来讲,要避免这个不命中,方法如下:
①在A数组访问第二行之前B数组不访问第二行。
②在A数组访问第二行之后B数组不访问第二行。
而如B[1][1]=A[1][1],得先访问A数组的A[1][1]才能得到B数组的B[1][1]。 采用方法①,然而由于最多定义12个变量,而for循环中占了4个,所以最多只能再用8个。发现B数组中第一行在不命中一次以后,对于这一行的访问以后一定是命中的,因为A数组不会再访问第一行了。故可将A数组第一行的元素先存入B数组的第一行,然后将A数组中的第二行读取以后再访问B数组中的第二行,这样一来就实现了方法①。
同理,我们可以同样地处理其余行,使得在对B数组的第i行进行访问时,A数组中的第i行已经被访问,以后A数组不会再访问第i行。
按照这个思路可以得到如下代码:
if(M == 32 && N == 32) {
for(i = 0; i < N; i += 8){
for(j = 0; j < M; j += 8){
if(i == j){
tmp0 = A[i][j];
tmp1 = A[i][j + 1];
tmp2 = A[i][j + 2];
tmp3 = A[i][j + 3];
tmp4 = A[i][j + 4];
tmp5 = A[i][j + 5];
tmp6 = A[i][j + 6];
tmp7 = A[i][j + 7];
B[i][j] = tmp0;
B[i][j + 1] = tmp1;
B[i][j + 2] = tmp2;
B[i][j + 3] = tmp3;
B[i][j + 4] = tmp4;
B[i][j + 5] = tmp5;
B[i][j + 6] = tmp6;
B[i][j + 7] = tmp7;
tmp0 = A[i + 1][j];
tmp1 = A[i + 1][j + 1];
tmp2 = A[i + 1][j + 2];
tmp3 = A[i + 1][j + 3];
tmp4 = A[i + 1][j + 4];
tmp5 = A[i + 1][j + 5];
tmp6 = A[i + 1][j + 6];
tmp7 = A[i + 1][j + 7];
B[i + 1][j] = B[i][j + 1];
B[i][j + 1] = tmp0;
B[i + 1][j + 1] = tmp1;
B[i + 1][j + 2] = tmp2;
B[i + 1][j + 3] = tmp3;
B[i + 1][j + 4] = tmp4;
B[i + 1][j + 5] = tmp5;
B[i + 1][j + 6] = tmp6;
B[i + 1][j + 7] = tmp7;
tmp0 = A[i + 2][j];
tmp1 = A[i + 2][j + 1];
tmp2 = A[i + 2][j + 2];
tmp3 = A[i + 2][j + 3];
tmp4 = A[i + 2][j + 4];
tmp5 = A[i + 2][j + 5];
tmp6 = A[i + 2][j + 6];
tmp7 = A[i + 2][j + 7];
B[i + 2][j] = B[i][j + 2];
B[i + 2][j + 1] = B[i + 1][j + 2];
B[i][j + 2] = tmp0;
B[i + 1][j + 2] = tmp1;
B[i + 2][j + 2] = tmp2;
B[i + 2][j + 3] = tmp3;
B[i + 2][j + 4] = tmp4;
B[i + 2][j + 5] = tmp5;
B[i + 2][j + 6] = tmp6;
B[i + 2][j + 7] = tmp7;
tmp0 = A[i + 3][j];
tmp1 = A[i + 3][j + 1];
tmp2 = A[i + 3][j + 2];
tmp3 = A[i + 3][j + 3];
tmp4 = A[i + 3][j + 4];
tmp5 = A[i + 3][j + 5];
tmp6 = A[i + 3][j + 6];
tmp7 = A[i + 3][j + 7];
B[i + 3][j] = B[i][j + 3];
B[i + 3][j + 1] = B[i + 1][j + 3];
B[i + 3][j + 2] = B[i + 2][j + 3];
B[i][j + 3] = tmp0;
B[i + 1][j + 3] = tmp1;
B[i + 2][j + 3] = tmp2;
B[i + 3][j + 3] = tmp3;
B[i + 3][j + 4] = tmp4;
B[i + 3][j + 5] = tmp5;
B[i + 3][j + 6] = tmp6;
B[i + 3][j + 7] = tmp7;
tmp0 = A[i + 4][j];
tmp1 = A[i + 4][j + 1];
tmp2 = A[i + 4][j + 2];
tmp3 = A[i + 4][j + 3];
tmp4 = A[i + 4][j + 4];
tmp5 = A[i + 4][j + 5];
tmp6 = A[i + 4][j + 6];
tmp7 = A[i + 4][j + 7];
B[i + 4][j] = B[i][j + 4];
B[i + 4][j + 1] = B[i + 1][j + 4];
B[i + 4][j + 2] = B[i + 2][j + 4];
B[i + 4][j + 3] = B[i + 3][j + 4];
B[i][j + 4] = tmp0;
B[i + 1][j + 4] = tmp1;
B[i + 2][j + 4] = tmp2;
B[i + 3][j + 4] = tmp3;
B[i + 4][j + 4] = tmp4;
B[i + 4][j + 5] = tmp5;
B[i + 4][j + 6] = tmp6;
B[i + 4][j + 7] = tmp7;
tmp0 = A[i + 5][j];
tmp1 = A[i + 5][j + 1];
tmp2 = A[i + 5][j + 2];
tmp3 = A[i + 5][j + 3];
tmp4 = A[i + 5][j + 4];
tmp5 = A[i + 5][j + 5];
tmp6 = A[i + 5][j + 6];
tmp7 = A[i + 5][j + 7];
B[i + 5][j] = B[i][j + 5];
B[i + 5][j + 1] = B[i + 1][j + 5];
B[i + 5][j + 2] = B[i + 2][j + 5];
B[i + 5][j + 3] = B[i + 3][j + 5];
B[i + 5][j + 4] = B[i + 4][j + 5];
B[i][j + 5] = tmp0;
B[i + 1][j + 5] = tmp1;
B[i + 2][j + 5] = tmp2;
B[i + 3][j + 5] = tmp3;
B[i + 4][j + 5] = tmp4;
B[i + 5][j + 5] = tmp5;
B[i + 5][j + 6] = tmp6;
B[i + 5][j + 7] = tmp7;
tmp0 = A[i + 6][j];
tmp1 = A[i + 6][j + 1];
tmp2 = A[i + 6][j + 2];
tmp3 = A[i + 6][j + 3];
tmp4 = A[i + 6][j + 4];
tmp5 = A[i + 6][j + 5];
tmp6 = A[i + 6][j + 6];
tmp7 = A[i + 6][j + 7];
B[i + 6][j] = B[i][j + 6];
B[i + 6][j + 1] = B[i + 1][j + 6];
B[i + 6][j + 2] = B[i + 2][j + 6];
B[i + 6][j + 3] = B[i + 3][j + 6];
B[i + 6][j + 4] = B[i + 4][j + 6];
B[i + 6][j + 5] = B[i + 5][j + 6];
B[i][j + 6] = tmp0;
B[i + 1][j + 6] = tmp1;
B[i + 2][j + 6] = tmp2;
B[i + 3][j + 6] = tmp3;
B[i + 4][j + 6] = tmp4;
B[i + 5][j + 6] = tmp5;
B[i + 6][j + 6] = tmp6;
B[i + 6][j + 7] = tmp7;
tmp0 = A[i + 7][j];
tmp1 = A[i + 7][j + 1];
tmp2 = A[i + 7][j + 2];
tmp3 = A[i + 7][j + 3];
tmp4 = A[i + 7][j + 4];
tmp5 = A[i + 7][j + 5];
tmp6 = A[i + 7][j + 6];
tmp7 = A[i + 7][j + 7];
B[i + 7][j] = B[i][j + 7];
B[i + 7][j + 1] = B[i + 1][j + 7];
B[i + 7][j + 2] = B[i + 2][j + 7];
B[i + 7][j + 3] = B[i + 3][j + 7];
B[i + 7][j + 4] = B[i + 4][j + 7];
B[i + 7][j + 5] = B[i + 5][j + 7];
B[i + 7][j + 6] = B[i + 6][j + 7];
B[i][j + 7] = tmp0;
B[i + 1][j + 7] = tmp1;
B[i + 2][j + 7] = tmp2;
B[i + 3][j + 7] = tmp3;
B[i + 4][j + 7] = tmp4;
B[i + 5][j + 7] = tmp5;
B[i + 6][j + 7] = tmp6;
B[i + 7][j + 7] = tmp7;
}
else {
for(k = i; k < i + 8; ++k) {
for(y = j; y < j + 8; ++y){
B[y][k] = A[k][y];
}
}
}
}
}
}
再考察64 * 64的矩阵:
对于64 * 64的矩阵而言,每一行元素会占8个组,因此4行元素即可占满cache。
尝试和32 * 32的矩阵相同的初始8 * 8分块方法,发现miss总数达到了4000+,基本没什么优化。此时对A数组的访问依然是第一个不命中。对B数组的访问,可以看到前4行和后四行所映射的块是相同的,于是访问完前四行的第一列后,访问后四行的第一列会冲突不命中,导致原来的块被驱逐,再访问前四行的第二列,由于之前的块已经被驱逐,因此又会miss且驱逐,如此反复下去,B数组中所有的元素皆会不命中。故不能采用8 * 8的划分方式。又因为4 * 4的分块方式无法充分利用每次加载后的块,故也将其否定。
考虑将8 * 8和4 * 4相结合。
下面用示意图进行表示:
红色块移至目的地,黄色块暂存至红色块右边且移动是伴随着转置的。
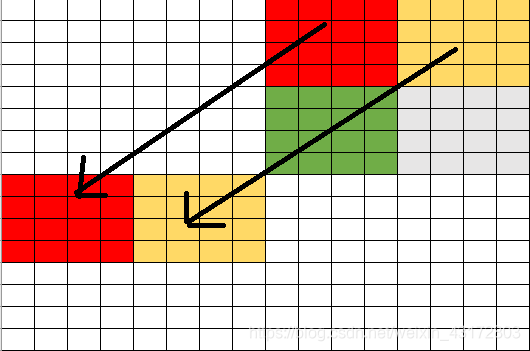
再实现图中的移动即可,将黄色块移到红色块的下面,在将绿色快移到之前“暂存”黄色块的地方,最后将灰色块移动到目的地即可。
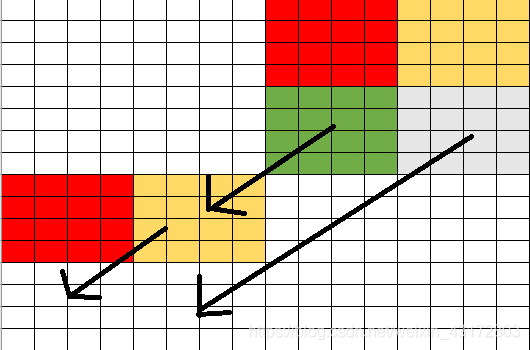
由上两种思路可同理写出61 * 67的代码。
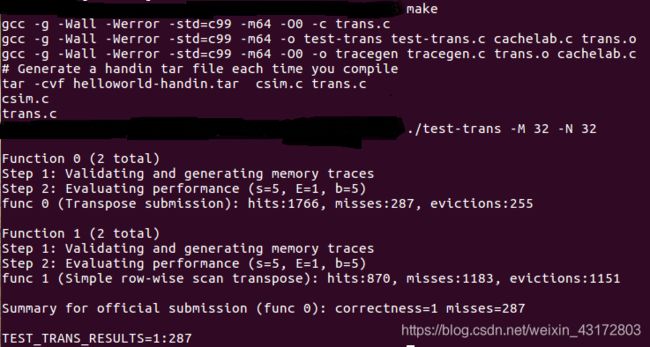
根据反复调整分块的大小,发现分成17 * 17的块时miss数最小,代码如下

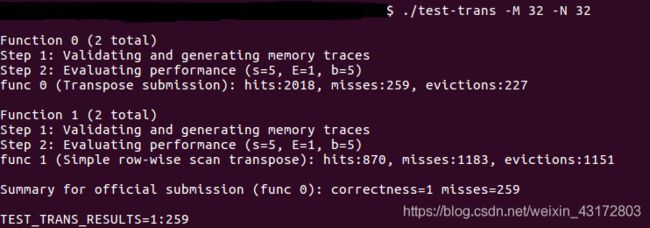
32×32(10分):运行结果截图
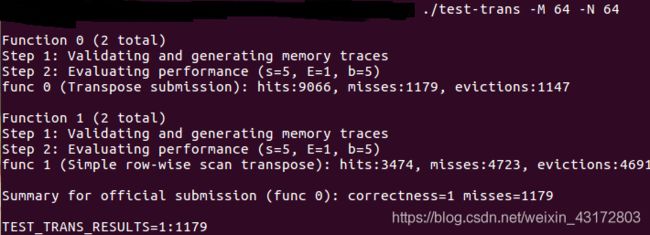
64×64(10分):运行结果截图
61×67(20分):运行结果截图

以下是程序相应代码
csim.c
#include -E -b -t \n" , argv[0]);
printf("Options:\n");
printf(" -h Print this help message.\n");
printf(" -v Optional verbose flag.\n");
printf(" -s Number of set index bits.\n" );
printf(" -E Number of lines per set.\n" );
printf(" -b Number of block offset bits.\n" );
printf(" -t Trace file.\n" );
printf("\nExamples:\n");
printf(" linux> %s -s 4 -E 1 -b 4 -t traces/yi.trace\n", argv[0]);
printf(" linux> %s -v -s 8 -E 2 -b 4 -t traces/yi.trace\n", argv[0]);
exit(0);
}
/*
* main - Main routine
*/
int main(int argc, char* argv[])
{
char c;
while( (c=getopt(argc,argv,"s:E:b:t:vh")) != -1){
switch(c){
case 's':
s = atoi(optarg);
break;
case 'E':
E = atoi(optarg);
break;
case 'b':
b = atoi(optarg);
break;
case 't':
trace_file = optarg;
break;
case 'v':
verbosity = 1;
break;
case 'h':
printUsage(argv);
exit(0);
default:
printUsage(argv);
exit(1);
}
}
/* Make sure that all required command line args were specified */
if (s == 0 || E == 0 || b == 0 || trace_file == NULL) {
printf("%s: Missing required command line argument\n", argv[0]);
printUsage(argv);
exit(1);
}
/* Compute S, E and B from command line args */
S = 1 << s;
B = 1 << b;
E = E;
/* Initialize cache */
initCache();
#ifdef DEBUG_ON
printf("DEBUG: S:%u E:%u B:%u trace:%s\n", S, E, B, trace_file);
printf("DEBUG: set_index_mask: %llu\n", set_index_mask);
#endif
replayTrace(trace_file);
/* Free allocated memory */
freeCache();
/* Output the hit and miss statistics for the autograder */
printSummary(hit_count, miss_count, eviction_count);
return 0;
}
trans.c
/*
* trans.c - Matrix transpose B = A^T
*
* Each transpose function must have a prototype of the form:
* void trans(int M, int N, int A[N][M], int B[M][N]);
*
* A transpose function is evaluated by counting the number of misses
* on a 1KB direct mapped cache with a block size of 32 bytes.
*/
#include