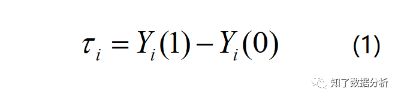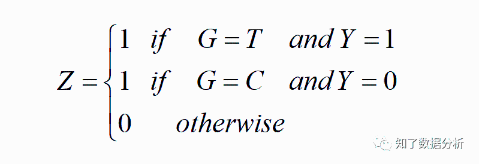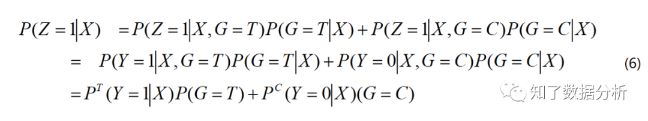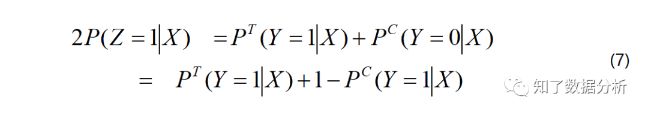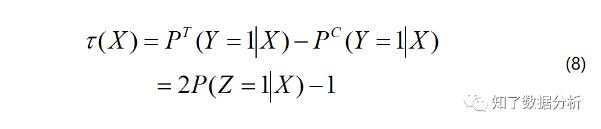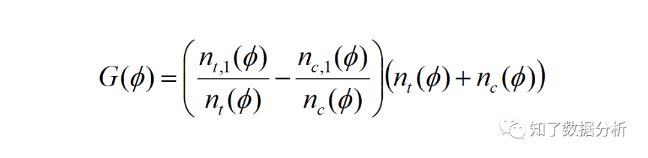【转】增益模型营销逻辑再理解
如何用增益模型,探讨精准营销的底层逻辑?(营销逻辑)-正经科普
借助Canvas黑魔法,实现营销增益模型Uplift Model | 人人都是产品经理
随着移动互联网的普及以及人工智能技术的不断发展,精准营销的理念正逐步渗透到各行各业以及人们生活的方方面面。但是如何通过数据挖掘出“营销敏感人群”,而不把成本浪费在“本来就会转化”的那部分人身上,成为智能营销时代的关键挑战。增益模型(uplift model)是目前解决这一痛点最好的方法之一,本文将试图通过该模型探讨智能营销的底层逻辑。
背景:问题先行
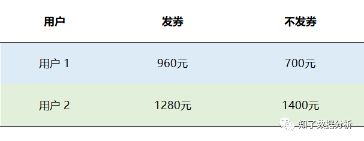
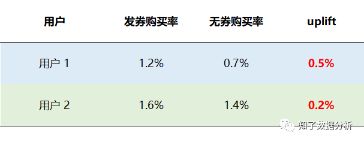
假设我们现在要搞一个优惠券促销活动,通过历史数据预测了两类用户发券购买率和无券购买率的结果(见下图),接下来我们想要对用户发放优惠券,这时会面临一个必须要解决的问题:给哪类用户发放优惠券能够使总收益最大化呢?
01 什么是增益模型(uplift model)
想要知道应该给哪一类用户发放优惠券,我们需要搞清楚哪一类用户对优惠券刺激最敏感,换言之,也就是需要对用户进行分类,了解每一类用户的特点。在营销活动中,对用户进行主动干预称为treatment,例如发放优惠券是一次treatment。根据是否对用户进行干预以及干预结果,我们可以将用户分为以下四类:
- Persuadables:基本只有在发券才会购买的人群,即优惠券敏感人群;
- Sure things:无论是否发券,都会购买,自然转化人群;
- Lost causes:无论是否发券都不购买,这类用户难以刺激,直接放弃;
- Sleeping dogs:与Persuadables相反,对营销活动比较反感,不发券的时候可能会购买,但发券后不会再购买。
对发放优惠券这种有成本的营销活动,我们不可能对所有用户都发放补贴,这个成本是任何企业都无法承受的。考虑到每个用户对价格的接受程度是不一样的,根据“营销四象限人群”分布,我们希望模型触达的是营销敏感的用户,即通过发放优惠券促进用户购买,而对于其他用户,最好不要发券,这样才能最大程度的节省成本。
我们再来看背景中的小例子,用户2发券后购买率(1.6%)明显高于用户1(1.2%),似乎我们应该对用户2发放优惠券,更能刺激其产生购买。但事实真的是这样吗?
假设用户1和用户2各1000人,不发券产品价格是100元,发放优惠券后价格是80元,我们可以有四种方案:用户1和2都发放优惠券、用户1和2都不发放优惠券、1发2不发、2发1不发。我们分别来计算一下这四种方案带来的总收益:
- 都发券:1000*1.2%*80+1000*1.6%*80=2240元
- 都不发券:1000*0.7%*100+1000*1.4%*100=2100元
- 1发2不发:1000*1.2%*80+1000*1.4%*100=2360元
- 2发1不发:1000*0.7%*100+1000*1.6%*80=1980元
通过计算四种方案的收益,我们发现实际情况和预想的并不一样,给发券购买率更高的用户2发放优惠券反而收益是最低的,这是为什么呢?
我们来进一步分析一下,除了发券购买率之外,我们还能知道这两类用户在没有优惠券情况下的自然购买率,根据这两个数据能够计算出发放优惠券所带来的增量效用。用户1的发券购买率虽然低,但在没有优惠券刺激情况下的购买率更低,即优惠券所带来的增量反而是比用户2更高,而我们做营销活动的目的是最大化总体的收益,本质是最大化优惠券的增量,因此我们应该向用户1发放优惠券。
通过这个小例子,我们能够得到一个结论:响应模型(reponse model)能够预测用户的购买概率,但是该模型不能告诉我们这批人是否因为发放优惠券而产生购买,这样我们就无法区分营销敏感(Persuadables)和自然转化(Sure things)这两类人群。也就是说响应模型(reponse model)很有可能会误导我们做出错误的决策。
而增益模型(uplift model)要做的就是帮助我们找到这些营销敏感人群,准确判断营销干预所带来的“增量提升”,从而促使营销推广效率的最大化,而不是把营销预算浪费在“本来就会转化”的那部分人身上。如果用一句话总结增益模型(uplift model):通过用户分群的方法对用户进行精细化运营的一种科学手段。
为了帮助大家更好的理解增益模型,我们构造这样一个场景:假设有N个用户,Yi(1)表示我们对用户i干预后的结果,比如给用户i发放优惠券后(干预)用户下单(结果),Yi(0)表示没有对用户干预的情况下用户的输出结果,比如没有给用户i发放优惠券(干预),用户下单(结果)。如下图所示:
那么,用户i的因果效应(causal effect)的计算如下:
增益模型的目标就是最大化这个增量,即有干预策略相对于无干预策略的提升,简单讲就是干预前后结果的差值。实际使用时会取所有用户的因果效应期望的估计值来衡量整个用户群的效果,称为条件平均因果效应(Conditional Average Treatment Effect, CATE)。
上式中Xi是用户i的特征,所谓的conditional指基于用户特征。
(2)式是理想的增益模型计算形式,实际上,对一个用户i我们不可能同时观察到使用策略(treatment)和未使用策略(control)的输出结果,即不可能同时得到Yi(1)和Yi(0)。因为对某个用户,我们要么发优惠券,要么不发。所以,我们可以将(2)式修改为:
其中Yi(obs)是用户i可以观察到的输出结果,Wi是一个二值变量,如果对用户i使用了策略,Wi=1,否则Wi=0。
在条件独立的假设下,条件平均因果效应的期望估计值是:
上式要满足条件独立(CIA)的条件,即用户特征与干预策略是相互独立的。
增益模型要优化τ(Xi),值越高越好。然而一个用户不能同时观察到使用干预策略和不使用干预策略的结果,因此τ(Xi)是难以直接优化的。但如果通过AB实验,可以获得使用干预策略和不使用干预策略两组人群,如果两组人群的特征分布一致,可以通过模拟两组人群的τ(Xi)得到个体用户的τ(Xi)。因此增益模型依赖AB实验的数据。
需要说明的一点是,增益模型(uplift model)是一组用于相同目的的建模方法的总称。下面就给小伙伴们介绍三种常用的增益模型建模方法。
02 常用uplift建模方法
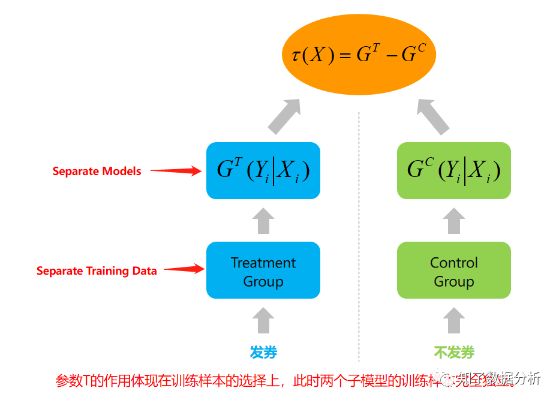
2.1 双模型(Two Model, T-Learner)
模型公式1:
建模过程:
以优惠券发放为例,目标是用户是否下单。训练时取实验组的用户训练,正样本是下单用户,负样本是未下单用户,预测结果是每个用户下单的概率。类似地,对照组也可以使用另一个模型预测出每个用户下单的概率。两个组的用户下单概率求平均,即可得到:
两者相减即得到τ(X)。预测时,对用户分别使用G(T)和G(C)预测,两个模型预测的分数相减即得到预测用户i的τ(Xi),最后根据τ(Xi)的高低决定是否发券。
模型优点:
- 简单直观,容易理解
- 可以复用常见的机器学习模型(LR、Tree Model、NN)
模型缺点:
- 双模型打分误差累积
- 只是模拟了τ(Xi),没有真正优化τ(Xi)
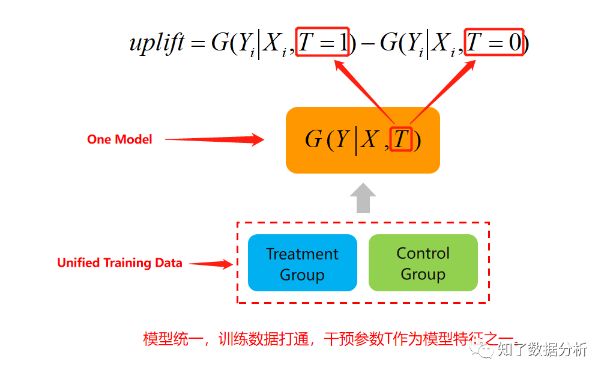
2.2 差分响应模型升级版(One-Model, Approach)
模型公式2:
建模过程:
差分响应模型的训练数据和模型都是各自独立的,可以分别在训练数据层面上打通以及在模型层面上打通,得到升级版的差分响应模型。
在实验组和对照组的用户特征中,加入与T有关的特征,实现数据层面的打通,即实验组和对照组合并,使用同一个模型训练。预测时将同一样本特征进行多次输入,每次只是改变不同的T值。这是阿里大文娱提到的一种方法。
模型优点:
- 模型训练数据,模型学习更充分
- 避免双模型打分误差累积
- 通过一个模型可以对multiple – treatment进行建模,实用性更强
模型缺点:
- 基础模型仍是响应模型,对uplift建模是间接的,模型效果还有提升空间
- 无法满足用户特征与条件策略独立的假设
2.3 Class TransformationMethod
另外一种更严谨的可以实现实验组对照组数据打通和模型打通的方法叫做class transformation method,可以直接优化τ(Xi)。
模型公式
定义一个变量G∈{T, C},G=T表示有干预,即实验组(treatment),G=C表示无干预,即对照组(control)。uplift分数τ可以表示为:
为了统一表示实验组和对照组都下单的情况(Y=1),再定义一个变量Z,Z∈{0, 1}:
下面证明优化(5)式相当于优化P(Z=1∣X)。
假设干预策略G与用户特征X相互独立,即G独立于X:P(G∣X)=P(G),(5)式可以转写为:
注意到P(G=T)和P(G=C)是可以通过AB实验控制的,在随机化实验中,如果实验组和对照组的人数是相等的,那么P(G=T)=P(G=C)=1/2,即一个用户被分在实验组(有干预策略)和被分在对照组(无干预策略)的概率是相等的。
在该假设下,(6)式可以改写为:
由(7)式可得:
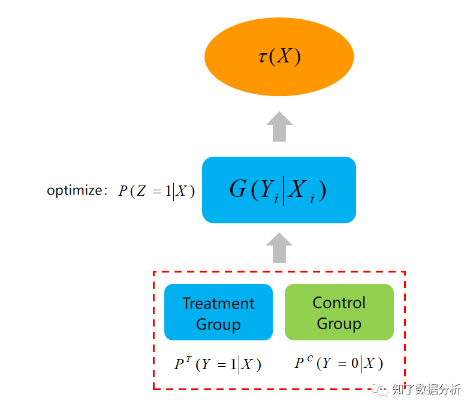
(8)式就是要计算的uplift score,此时只有Z一个变量,可以直接对Z=1建模,相当于优化P(Z=1∣X),而不需要分别对实验组P(T)和对照组P(C)单独建模。而P(Z=1∣X)可以通过任何分类模型得到,所以这个方法称为Class Transformation Method。
实际上,Z=1就是实验组中下单的用户和对照组中未下单的用户,因此可以直接将实验组和对照组用户合并,使用一个模型建模,实现了数据层面和模型层面的打通。预测时,模型预测的结果就是uplift score,这点与差分响应模型不同。
该方法需满足以下两个假设:
- G与X相互独立
- P(G=T)=P(G=C)=1/2,实践中并不一定能严格满足
03 如何评估uplift模型
根据uplift模型的定义,uplift score得分越高,代表该用户增益就越大。但因为增益模型中不可能同时观察到同一用户在不同干预策略下的响应,因此无法直接计算上述评价指标。增益模型通常都是通过划分十分位数(decile)来对齐实验组和对照组数据从而进行间接评估,而不是在一个测试集上直接评估。
接下来主要给家介绍三种主要的评估方法。
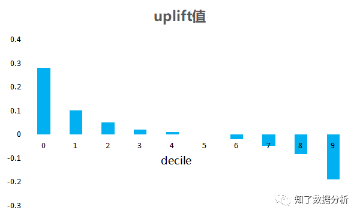
3.1 uplift 柱状图
测试集上,实验组和对照组的用户分别按照uplift由高到低排序,划分为十等份,即十分位(decile),分别是Top 10%、Top 20% …… Top 100%用户。分别对实验组和对照组中每个十分位内的用户求E[Y(T)∣X(T)] 和E[Y(C)∣X(C)],即预测分数的均值,然后相减,作为这个十分位bin内的uplift,绘制柱状图,如下图:
这种方法只能定性分析,无法计算出一个具体的值来整体评价模型的好坏。
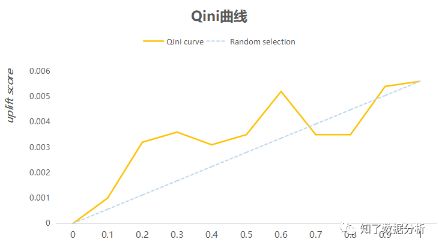
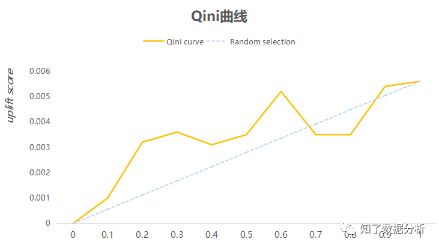
3.2 Qini曲线(Qini curve)
可以在uplift bars的基础上绘制曲线,类似AUC来评价模型的表现,这条曲线称为Qini curve,计算每个百分比的Qini系数,最后将这些Qini系数连接起来,得到一条曲线。Qini系数计算如下:
ϕ是按照uplift score由高到低排序的用户数量占实验组或对照组用户数量的比例,如ϕ=0.1,表示实验组或对照组中前10%的用户。
如上图,蓝色是随机曲线,橙色是Qini曲线,Qini曲线与随机曲线之间的面积作为评价模型的指标,面积越大,表示模型结果远超过随机选择的结果,与AUC类似,这个指标称为AUUC(Area Under Uplift Curve)。可以看到,当横轴等于0.6时,对应的纵轴大概是0.0052(uplift score),表示当uplift score等于0.0052时,可以覆盖前60%的用户数量,这部分用户就是营销活动的目标用户(persuadables)。
Qini系数分母是实验组和对照组的全体用户数,如果两组用户数量差别比较大,就会导致结果指标失真。另一种累积增益曲线可以避免这个问题。
3.3累积增益曲线(Cumulative Gain curve)
累积增益曲线计算如下:
该公式中各符号含义与Qini系数符号含义相同。与Qini系数相比,累积增益的分母是百分比ϕ下的实验组或对照组人数,并乘以nt(ϕ)+nc(ϕ)作为全局调整系数,避免实验组和对照组用户数量不平衡导致的指标失真问题。
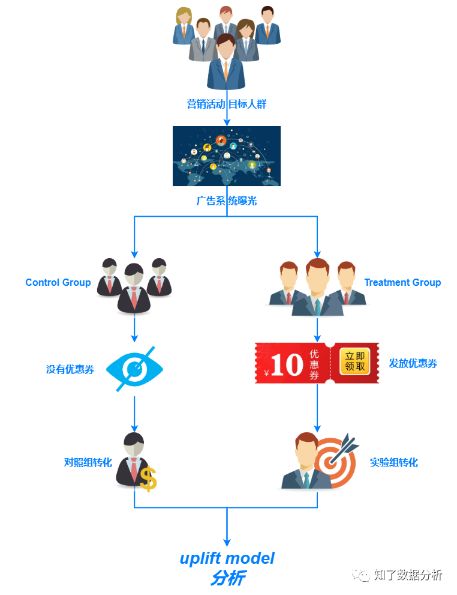
04 uplift精准营销流程
最后,我们通过下面这张图直观的总结一下,在实际工作中是如何通过uplift模型进行精准营销的: