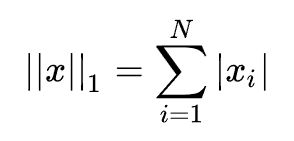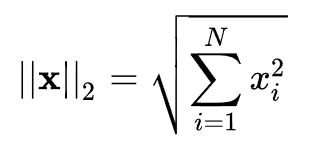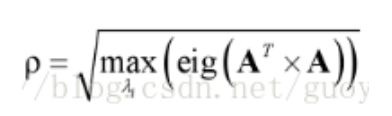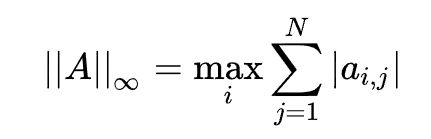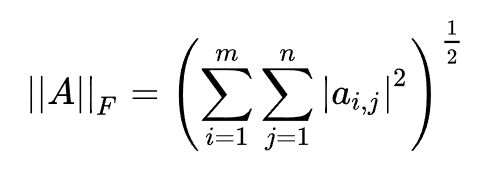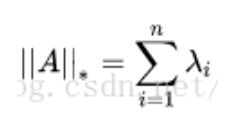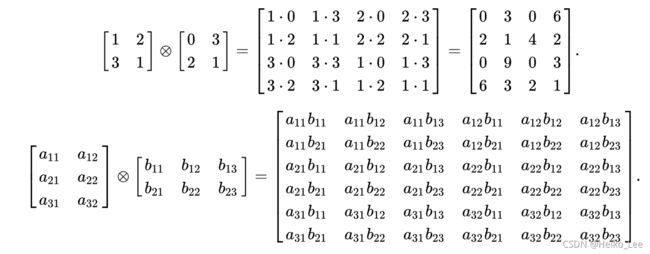机器学习中的数学基础 DAY 2

向量、矩阵、张量

张量（英语：Tensor）是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数，这些线性关系的基本例子有内积、外积、线性映射以及笛卡儿积。其坐标在n维空间内，有n^r个分量的一种量，其中每个分量都是坐标的函数，而在坐标变换时，这些分量也依照某些规则作线性变换。r称为该张量的秩或阶（与矩阵的秩和阶均无关系）。

在同构的意义下，第零阶张量（r=0）为标量，第一阶张量（r=1）为矢量， 第二阶张量（r=2）则成为矩阵。例如，对于3维空间，r=1时的张量为此矢量：(x,y,z）^T。由于变换方式的不同，张量分成“协变张量”（指标在下者）、“逆变张量”（指标在上者）、“混合张量”（指标在上和指标在下两者都有）三类。

向量与矩阵运算

一、向量范数

1.1、 0-范数

严格说不属于范数，向量中非零元素的个数。

1.2、 1范数

即向量元素绝对值之和，matlab调用函数norm(x, 1) 。

1.3、 2范数

Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，matlab调用函数norm(x, 2)。

1.4、 p范数

即向量元素绝对值的p次方和的1/p次幂，matlab调用函数norm(x, p)。

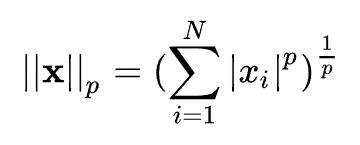
1.5、 ∞范数

即所有向量元素绝对值中的最大值，matlab调用函数norm(x, inf)。

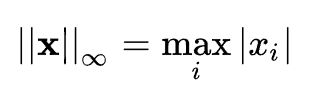
1.6、 -∞范数

即所有向量元素绝对值中的最小值，matlab调用函数norm(x, -inf)。

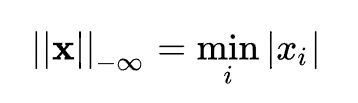
二、矩阵范数

2.1、 1范数

列和范数，即所有矩阵列向量绝对值之和的最大值，matlab调用函数norm(A, 1)。

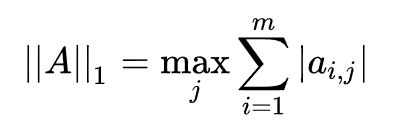
2.2、 2范数

对于实矩阵A，它的谱范数定义为：

其中，eig(X)为计算方阵X特征值，它返回特征值向量：

谱范数，即A’A矩阵的最大特征值的开平方。matlab调用函数norm(x, 2)。

2.3、 ∞范数

行和范数，即所有矩阵行向量绝对值之和的最大值，matlab调用函数norm(A, inf)。

2.4、F-范数

Frobenius范数，即矩阵元素绝对值的平方和再开平方，matlab调用函数norm(A, ’fro‘)。

2.5、核范数

是A的奇异值。核范数即奇异值之和。
三、向量点乘和叉乘

向量的内积（点乘）：

向量的外积（叉乘）：

四、哈达玛（hadamard）积

哈达玛积(Hadamard product)是矩阵的一类运算，若A=(aij)和B=(bij)是两个同阶矩阵，若cij=aij×bij,则称矩阵C=(cij)为A和B的哈达玛积，或称基本积

五、克罗内克（Kronecker）积

数学上，克罗内克积是两个任意大小的矩阵间的运算。克罗内克积是张量积的特殊形式，以德国数学家利奥波德·克罗内克命名。

定义：

例子：

矩阵的逆与伪逆

逆矩阵

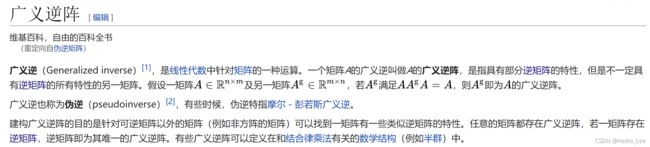
伪逆（广义逆阵）

行列式性质

矩阵分解

一、LU分解
在线性代数与数值分析中，LU分解是矩阵分解的一种，将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积，有时需要再乘上一个置换矩阵。LU分解可以被视为高斯消元法的矩阵形式。在数值计算上，LU分解经常被用来解线性方程组、且在求反矩阵和计算行列式中都是一个关键的步骤。

二、奇异值分解
奇异值分解（singular value decomposition）是线性代数中一种重要的矩阵分解，在信号处理、统计学等领域有重要应用。奇异值分解在某些方面与对称矩阵或厄米矩阵基于特征向量的对角化类似。然而这两种矩阵分解尽管有其相关性，但还是有明显的不同。对称阵特征向量分解的基础是谱分析，而奇异值分解则是谱分析理论在任意矩阵上的推广。

三、特征值分解
线性代数中，特征分解（Eigendecomposition），又称谱分解（Spectral decomposition）是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。需要注意只有对可对角化矩阵才可以施以特征分解。

四、QR分解
QR分解法是三种将矩阵分解的方式之一。这种方式，把矩阵分解成一个正交矩阵与一个上三角矩阵的积。QR分解经常用来解线性最小二乘法问题。QR分解也是特定特征值算法即QR算法的基础。