因子分析原理及其python实现

本文参考数学建模清风老师课件编写。

一、概述

因子分析由斯皮尔曼在1904年首次提出，其在某种程度上可以被看成是主成分分析的推广和扩展。因子分析法通过研究变量间的相关系数矩阵，把这些变量间错综复杂的关系归结成少数几个综合因子，由于归结出的因子个数少于原始变量的个数，但是它们又包含原始变量的信息，所以，这一分析过程也称为降维。由于因子往往比主成分更易得到解释，故因子分析比主成分分析更容易成功，从而有更广泛的应用。

基本思想： 根据相关性大小把变量分组，使得同组内的变量之间相关性较高，但不同组的变量不相关或相关性较低，每组变量代表一个基本结构一即公共因子。
两个核心问题： 一是如何构造因子变量，二是如何对因子变量进行命名解释。
因子分析类型： R型因子分析与Q型因子分析，就像聚类分析分为R型和Q型一样，R型的因子分析是对变量作因子分析，Q型因子分析是对样品作因子分析。

二、因子分析与主成分对比

假设有 $n$ 个样本, $p$ 个指标, 则可构成大小为 $n\times p$ 的样本矩阵 $x=\left[\begin{array}{cccc}{x}_{21}& x_{22}& \cdots & x_{2p}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{np}\end{array}\right]=\left(x_1,x_2,\cdots ,x_p\right)$

主成分分析： $x_1,x_2,\cdots ,x_p\Rightarrow z_1,z_2,\cdots ,z_m(m\le p)$, 且它们满足: $\{\begin{array}{c}{z}_1=l_{11}{x}_1+l_{12}{x}_2+\cdots +l_{1p}{x}_p\\ z_2=l_{21}{x}_1+l_{22}{x}_2+\cdots +l_{2p}{x}_p\\ ⋮\\ z_m=l_{m1}{x}_1+l_{m2}{x}_2+\cdots +l_{mp}{x}_p\end{array}$

$z_1,z_2,\cdots ,z_m$ 是 $m$ 个主成分, 可以看出, 主成分实际上就是各指标的线性组合。

因子分析： $x_1,x_2,\cdots ,x_p\Rightarrow f_1,f_2,\cdots ,f_m(m\le p)$, 且它们满足: $\{\begin{array}{c}{x}_1=u_1+a_{11}{f}_1+a_{12}{f}_2+\cdots +a_{1m}{f}_m+{\epsilon }_1\\ x_2=u_2+a_{21}{f}_1+a_{22}{f}_2+\cdots +a_{2m}{f}_m+{\epsilon }_2\\ ⋮\\ x_p=u_p+a_{p1}{f}_1+a_{p2}{f}_2+\cdots +a_{pm}{f}_m+{\epsilon }_p\end{array}$
$f_1,f_2,\cdots ,f_m$ 被称为公共因子, ${\epsilon }_i$ 为特殊因子, 各因子的线性组合构成了原始的指标。
(有点像回归, 回归中自变量是已知的, 因子分析是只知道因变量, 要我们来找自变量)
其他主要区别:

1. 主成分分析只是简单的数值计算, 不需要构造一个模型, 几平没什么假定；而因子分析需要构造一个因子模型，并伴随几个关键性的假定。
2. 主成分的解是唯一的，而因子可有许多解。
3. 主成分分析把方差划分为不同的正交成分，而因子分析则把方差划归为不同的起因因子
4. 因子分析中特征值的计算只能从相关系数矩阵出发，且必须将主成分转换成因子。

联系：

1. PCA和因子分析都是数据降维的重要方法，都对原始数据进行标准化处理，都消除了原始指标的相关性对综合评价所造成的信息重复的影响，都属于因素分析法，都基于统计分析方法；
2. 二者均应用于高斯分布的数据，非高斯分布的数据采用ICA算法；
3. 二者构造综合评价时所涉及的权数具有客观性，在原始信息损失不大的前提下，减少了后期数据挖掘和分析的工作量。

因子解释成功的可能性要远大于主成分解释成功的可能性。

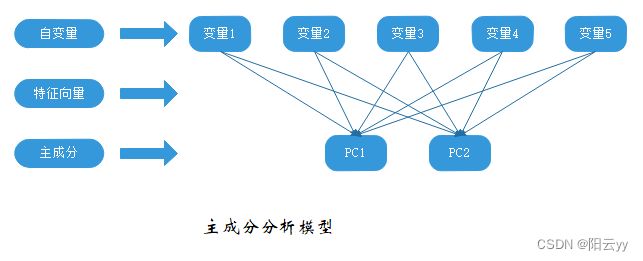
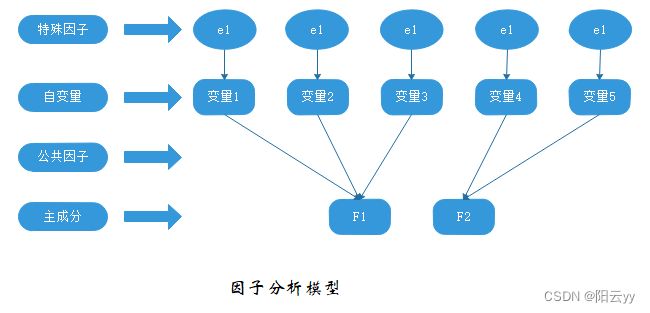
PCA与FA对比图解：

主成分（PC1和PC2）是自变量(1-5)的线性组合。形成线性组合的权重都是通过最大化各主成分所解释的方差来获得，同时还要保证个主成分间不相关。相反，因子(F1、F2)被当做是自变量的结构基础或“原因”，而不是它们的线性组合。代表自变量方差的误差（e1到e5）无法用因子来解释。图中的椭圆表示因子和误差无法直接观测，但是可通过变量间的相互关系推导得到。

三、因子分析原理

假设大小为 $n\times p$ 的随机向量 $x=\left(x_1,x_2,\cdots ,x_p\right)$ 的均值 $u=\left(u_1,u_2,\cdots u_p\right)$, 协方差矩阵 ${\Sigma }_{p\times p}=\left({\sigma }_{ij}\right)$
因子分析的一般模型为: $\{\begin{array}{c}{x}_1=u_1+a_{11}{f}_1+a_{12}{f}_2+\cdots +a_{1m}{f}_m+{\epsilon }_1\\ x_2=u_2+a_{21}{f}_1+a_{22}{f}_2+\cdots +a_{2m}{f}_m+{\epsilon }_2\\ ⋮\\ x_p=u_p+a_{p1}{f}_1+a_{p2}{f}_2+\cdots +a_{pm}{f}_m+{\epsilon }_p\end{array}$

其中 $f_1,f_2,\cdots ,f_m$ 被称为公共因子, ${\epsilon }_i(i=1,2,\cdots ,p)$ 为特殊因子, 它们都是无法观测的随机变量。
公共因子 $f_1,f_2,\cdots ,f_m$ 出现在每一个原始变量 $x_i(i=1,2,\cdots ,p)$ 的表达式中, 可以理解为原始变量共同 拥有的某些特征 (具有共同的影响因素) ; 每个特殊因子 ${\epsilon }_i(i=1,2,\cdots ,p$ )仅仅出现在与之相应的 第 $i$ 个原始变量 $x_{\mathrm{i}}$ 的表达式中, 它只对这个原始变量起作用。
上面这个式子我们用矩阵形式可记为:
$$x=u+Af+\epsilon$$
其中 $f={\left(f_1,f_2,\cdots ,f_m\right)}^{\top }(m\le p)$ 为公因子向量, $\epsilon ={\left({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_p\right)}^{\top }$ 为特殊因子向量, $A_{p\times m}=\left(a_{ij}\right)$ 称为 因子载荷矩阵, 并假设 $A$ 的秩为 $m$.
要进行因子分析, 必须要解出 $A$ 这个矩阵, 因此下面我们要给的一些假设用来计算 $A$ 矩阵。

四、因子分析模型的假设

因子分析模型：
$$\begin{array}{rl}& x=\{\begin{array}{c}{x}_1=u_1+a_{11}{f}_1+a_{12}{f}_2+\cdots +a_{1m}{f}_m+{\epsilon }_1\\ x_2=u_2+a_{21}{f}_1+a_{22}{f}_2+\cdots +a_{2m}{f}_m+{\epsilon }_2\\ ⋮\\ x_p=u_p+a_{p1}{f}_1+a_{p2}{f}_2+\cdots +a_{pm}{f}_m+{\epsilon }_p\end{array}=u+Af+\epsilon \\ & \text{假设 ,}\{\begin{array}{l}E(f)=0\\ E(\epsilon )=0\\ \mathrm{Var}(f)=I\\ \mathrm{Var}(\epsilon )=D=\mathrm{diag}\left({\sigma }_1^2,{\sigma }_2^2,\cdots ,{\sigma }_p^2\right)\\ \mathrm{cov}(f,\epsilon )=E\left(f{\epsilon }^{\top }\right)=0\end{array}\end{array}$$
其中 $f={\left(f_1,f_2,\cdots ,f_m\right)}^{\top }(m\le p)$ 为公因子向量
$\epsilon ={\left({\epsilon }_1,{\epsilon }_2,\cdots ,{\epsilon }_p\right)}^{\top }$ 为特殊因子向量
$A_{p\times m}=\left(a_{ij}\right)$ 称为因子载荷矩阵, 并假设 $A$ 的秩为 $m$.
公因子彼此不相关, 且具有单位方差; 特殊因子彼此不相关且与公因子也不相关。

五、因子载荷矩阵的统计意义

1. $A$ 的元素 $a_{ij}$ : 原始变量 $x_i$ 与公因子 $f_j$ 之间的协方差: $a_{ij}=\mathrm{cov}\left(x_i,f_j\right)$
   如果 $x$ 经过了标准化, 则 $a_{ij}=\rho \left(x_i,f_j\right)(x_i$ 和 $f_j$ 的相关系数 $)$
2. $A$ 的行元素平方和 $h_i^2={\sum }_{j=1}^m{a}_{ij}^2$ : 原始变量 $x_i$ 对公因子依赖的程度
   可以证明: $\mathrm{Var}\left(x_i\right)=h_i^2+{\sigma }_i^2(i=1,2,\cdots ,p)$
   $h_i^2$ 反应了公因子对于 $x_i$ 的影响, 可以看成是公因子对于 $x_i$ 的方差贡献，称为共性方差; 而 ${\sigma }_i^2$ 是特殊 因子 ${\epsilon }_i$ 对 $x_i$ 的方差贡献, 称为个性方差。如果 $x$ 经过了标准化, 则 $h_i^2+{\sigma }_i^2=1$.
3. $A$ 的列元素平方和 $g_j^2={\sum }_{i=1}^p{a}_{ij}^2$ : 公因子 $f_j$ 对 $x$ 的贡献
   可以证明:
   $$\begin{array}{rl}\sum _{i=1}^p\mathrm{Var}\left(x_i\right)& =\sum _{i=1}^p{a}_{i1}^2\mathrm{Var}\left(f_1\right)+\sum _{i=1}^p{a}_{i2}^2\mathrm{Var}\left(f_2\right)+\cdots +\sum _{i=1}^p{a}_{im}^2\mathrm{Var}\left(f_m\right)+\sum _{i=1}^p\mathrm{Var}\left({\epsilon }_i\right)\\ & =g_1^2\mathrm{Var}\left(f_1\right)+g_2^2\mathrm{Var}\left(f_2\right)+\cdots +g_m^2\mathrm{Var}\left(f_m\right)+\sum _{i=1}^p{\sigma }_i^2\\ & =g_1^2+g_2^2+\cdots +g_m^2+\sum _{i=1}^p{\sigma }_i^2\end{array}$$
   从上述的推导中可以看出, $A$ 的第 $j$ 列元素的平方和 $g_j^2$ 是 $\mathrm{Var}\left(f_j\right)$ 的系数, $g_j^2$ 的值越大, 反映了 $f_j$ 对 $x$ 的影响越大, $g_j^2$ 是衡量公因子 $f_j$ 重要性的一个尺度, 可视为公因子 $f_j$ 对 $x$ 的贡献。

六、因子模型的性质

1. $x$ 的协方差矩阵 $\Sigma$ 的分解
   $$\begin{array}{r}x=u+Af+\epsilon ，\text{ 假设 }\{\begin{array}{l}E(f)=0\\ E(\epsilon )=0\\ \mathrm{Var}(f)=I\\ \mathrm{Var}(\epsilon )=D=\mathrm{diag}\left({\sigma }_1^2,{\sigma }_2^2,\cdots ,{\sigma }_p^2\right)\\ \mathrm{cov}(f,\epsilon )=E\left(f{\epsilon }^{\top }\right)=0\end{array}\end{array}$$
   $$\begin{array}{rl}\mathrm{Var}(x)& =E\left[(x-u)(x-u{)}^{\top }\right]=E\left[(Af+\epsilon )(Af+\epsilon {)}^{\top }\right]\\ & =AE\left(f{f}^{\top }\right)A^{\top }+AE\left(f{\epsilon }^{\top }\right)+E\left(\epsilon f^{\top }\right)A^{\top }+E\left(\epsilon {\epsilon }^{\top }\right)\\ & =A\mathrm{Var}(f)A^{\top }+\mathrm{Var}(\epsilon )\\ & =A{A}^{\top }+D\end{array}$$
2. 因子载荷不唯一
   令 $T$ 为任意一个 $m\times m$ 的正交矩阵, 令 $A^{\ast }=AT,f^{\ast }=T^{\top }f$, 则模型可表示为:
   $$x=u+A^{\ast }{f}^{\ast }+\epsilon \text{, 因为假设仍然成立 }\{\begin{array}{l}E\left(f^{\ast }\right)=T^{\top }E(f)=0\\ E(\epsilon )=0\\ \mathrm{Var}\left(f^{\ast }\right)=T^{\top }\mathrm{Var}(f)T=T^{\top }IT=I\\ \mathrm{Var}(\epsilon )=D=\mathrm{diag}\left({\sigma }_1^2,{\sigma }_2^2,\cdots ,{\sigma }_p^2\right)\\ \mathrm{cov}\left(f^{\ast },\epsilon \right)=E\left(f^{\ast }{\epsilon }^{\top }\right)=T^{\top }E\left(f{\epsilon }^{\top }\right)=0\end{array}$$
   正是因为因子载荷矩阵A不是唯一的，在实际的应用中我们常常利用这一点，通过因子的变换，使得新的因子具有更容易解释的实际意义。这就是因子分析往往比主成分分析的结果更容易解释的原因。

七、参数估计

设 $x_1,x_2,\cdots ,x_n$ 是一组 $p$ 维样本, 则 $u$ 和 $\Sigma$ 可分别估计为: $\bar{x}=\frac{1}{n}{\sum }_{i=1}^n{x}_i$ 和 $S^2=\frac{1}{n}{\sum }_{i=1}^n\left(x_i-\bar{x}\right){\left(x_i-\bar{x}\right)}^{\top }$ 为了建立因子模型, 我们需要估计出因子载荷矩阵 $A_{p\times m}=\left(a_{ij}\right)$, 以及个性方差矩阵 $D=\mathrm{diag}\left({\sigma }_1^2,{\sigma }_2^2,\cdots ,{\sigma }_p^2\right)$.

参数估计方法：
主成分法: 假设变量是因子的线性组合, 第一主成分有最大的方差, 后续主成 分所解释的方差逐渐减小, 各主成分之间互不相关, 主成分法通常用来计算初 始公因子, 它也适用于相关矩阵为奇异时的情况。

设 ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_p$ 为样本相关系数矩阵 R 的特征值, ${\eta }_1,{\eta }_2,\cdots ,{\eta }_p$为相应的标准正交化特征向量。设m

$$A=\left(\sqrt{{\lambda }_1}{\eta }_1,\sqrt{{\lambda }_2}{\eta }_2,\cdots ,\sqrt{{\lambda }_m}{\eta }_m\right)$$

特殊因子的方差用$R-A{A}^T$ 的对角元来估计, 即

$${\sigma }_i^2=1-\sum _{j=1}^m{a}_{ij}^2$$

末加权最小平方法: 使得观测的相关矩阵和再生的相关矩阵之差的平方和最小, 忽略对角元素。
综合最小平方法: 使得观测的相关矩阵和再生的相关矩阵之差的平方和最小,
并以变量单值的倒数对相关系数加权。
最大似然法: 假设样本来自多元正态分布, 使用极大使然估计。
主因子法: 从初始相关矩阵提取公共因子, 并把多元相关系数的平方置于对 角线上, 再用初始因子载荷估计新的变量共同度, 如此重复直至变量共同度在 两次相邻迭代中的变化达到临界条件。

主因子方法是对主成分方法的修正, 假定我们首先对变量进行标准化变换。则
$$\begin{array}{l}R=A{A}^T+D\\ R^{\ast }=A{A}^T=R-D\end{array}$$
称$R^{\ast }$ 为约相关系数矩阵, $R^{\ast }$对角线上的元素是$h_i^2$ , 而不是 1 。

$$R^{\ast }=R-D=\left[\begin{array}{cccc}{\hat{h}}_1^2& r_{12}& \cdots & r_{1p}\\ r_{21}& {\hat{h}}_2^2& \cdots & r_{2p}\\ ⋮& ⋮& & ⋮\\ r_{p1}& r_{p2}& \cdots & {\hat{h}}_p^2\end{array}\right]$$

直接求$R^{\ast }$的前$p$个特征值和对应的正交特征向量。得到如下的矩阵

$$A=\left[\begin{array}{llll}\sqrt{{\lambda }_1^{\ast }}{u}_1^{\ast }& \sqrt{{\lambda }_2^{\ast }}{u}_2^{\ast }& \cdots & \sqrt{{\lambda }_p^{\ast }}{u}_p^{\ast }\end{array}\right]$$

其中$R^{\ast }$ 的特征值: ${\lambda }_1^{\ast }\ge {\lambda }_2^{\ast }\ge \cdots \ge {\lambda }_p^{\ast }$ , 对应的正交特征向量为 $u_1^{\ast },u_2^{\ast },\cdots ,u_p^{\ast }$ 。
在实际应用中, 特殊因子的方差一般都是末知的, 可以通过一组样本来估计。估计 的方法有如下几种:

1. 取 ${\hat{h}}_i^2=1$ , 在这个情况下主因子解与主成分解等价。
2. 取 ${\hat{h}}_i^2=R_i^2$, $R_i^2$ 为 $x_i$ 与其它所有的原始变量 $x_j$ 的复相关系数的平方, 即 $x_i$ 对 其余的 $p-1$ 个 $x_j$ 的回归方程的判定系数，这是因为 $x_i$ 与公共因子的关系是通过其余 的 $p-1$ 个 $x_j$ 的线性组合联系起来的。
3. 取 ${\hat{h}}_i^2={\max }_{j\ne i}\left|r_{ij}\right|$ , 这意味着取 $x_i$ 与其余的 $x_j$ 的简单相关系数的绝对值最大者。
4. 取 $\widehat{h_i^2}=\frac{1}{p-1}{\sum }_{j=1;j\ne i}^p{r}_{ij}$ ，其中要求该值为正数。
5. 取 $h_i^2=\frac{1}{r^{ii}}$ ，其中 $r^{ii}是R^{-1}$ 的对角元素。

Alpha 因子法: 把当前分析变量看作是所有潜在变量的一个样本, 最大化因子 的Alpha可靠性。
映像因子法: 把每个变量的主要部分定义为其他各变量的线性回归, 而不是潜 在因子的函数。

最常用主成分法、最大似然法和主轴因子法。

七、因子旋转方法

得到因子模型后，其中的公共因子不一定能反映问题的实质特征，为了能更好地解释每一个公共因子的实际意义，且减少解释的主观性，可以通过因子旋转达到目的。因子旋转分为正交旋转与斜交旋转，经过正交旋转而得到的新的公共因子仍然保持彼此独立的性质，而斜交旋转得到的公共因子是相关的(违背了最初的假定，因此可以看作传统因子分析的拓展)，其实际意义更容易解释。但不论是正交旋转还是斜交旋转，都应当使新公共因子的载荷系数的绝对值尽可能接近0或1。

最大方差法 (Varimax Method)： 一种正交旋转方法, 它使得对每个因子有高负载的变量的数目达到最小。该 方法简化了因子的解释。
直接 Oblimin 方法： 一种斜交 (非正交) 旋转方法。当 delta 等于 0 (缺省值) 时, 解是最斜交的。 delta 负得越厉害, 因子的斜交度越低。要覆盖缺省的 delta 值 0 , 请输人小于等于 $0.8$ 的数。
最大四次方值法 (Quartimax Method)： 一种旋转方法, 它可使得解释每个变量所需的因子最少。该方法简化 了观察到的变量的解释。
最大平衡值法 (Equamax Method)： 一种旋转方法, 它是简化因子的最大方差法与简化变量的最大四次方值 法的组合。它可以使得高度依赖因子的变量的个数以及解释变量所需的因子的个数最少。
最优斜交旋转 (Promax Rotation)： 斜交旋转, 可使因子相关联。该旋转可比直接最小斜交旋转更快地计算出 来, 因此适用于大型数据集。

八、因子得分

因子分析是将变量表示为公共因子和特殊因子的线性组合；此外, 我们可以反过来将公共因子表示为原变量的线性组合, 即可得到因子得分。
$$\{\begin{array}{l}{x}_1=u_1+a_{11}{f}_1+a_{12}{f}_2+\cdots +a_{1m}{f}_m+{\epsilon }_1\\ x_2=u_2+a_{21}{f}_1+a_{22}{f}_2+\cdots +a_{2m}{f}_m+{\epsilon }_2\\ ⋮\\ x_p=u_p+a_{p1}{f}_1+a_{p2}{f}_2+\cdots +a_{pm}{f}_m+{\epsilon }_p\end{array}\Rightarrow \{\begin{array}{c}{f}_1=b_{11}{x}_1+b_{12}{x}_2+\cdots +b_{1p}{x}_p\\ f_2=b_{21}{x}_1+b_{22}{x}_2+\cdots +b_{2p}{x}_p\\ ⋮\\ f_m=b_{m1}{x}_1+b_{m2}{x}_2+\cdots +b_{mp}{x}_p\end{array}$$
第 $i$ 个因子的得分可写成 $f_i=b_{i1}{x}_1+b_{i2}{x}_2+\cdots +b_{ip}{x}_p(i=1,2,\cdots ,m)$ $b_{ij}$ 就是第 $i$ 个因子的得分对应于第 $j$ 个变量 $x_j$ 的系数
注：我们计算出因子得分函数的系数后，就能够求出所有的因子得分。

计算因子得分的可选方法有回归、Bartlett 和 Anderson-Rubin。

1. 回归法 (Regression Method). 一种估计因子得分系数的方法。生成的分数的平均值为 0 , 方差等于估计的因 子分数和真正的因子值之间的平方多相关性。即使因子是正交的, 分数也可能相关。
   不妨设
   $$\left[\begin{array}{c}{X}_1\\ X_2\\ ⋮\\ X_p\end{array}\right]=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1m}\\ a_{21}& a_{22}& \cdots & a_{2m}\\ ⋮& ⋮& & ⋮\\ a_{p1}& a_{p2}& \cdots & a_{pm}\end{array}\right]\left[\begin{array}{c}{F}_1\\ F_2\\ ⋮\\ F_m\end{array}\right]+\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ ⋮\\ {\epsilon }_p\end{array}\right]$$

因子得分函数

$${\hat{F}}_j=b_{j1}{X}_1+\cdots +b_{jp}{X}_p,(j=1,2,\cdots ,m)$$

由于

$$\begin{array}{c}{a}_{ij}={\gamma }_{X_i{F}_j}=E\left(X_i{F}_j\right)=E\left[X_i\left(b_{j1}{X}_1+\cdots +b_{jp}{X}_p\right)\right]\\ =b_{j1}{\gamma }_{i1}+\cdots +b_{jp}{\gamma }_{ip}=\left[\begin{array}{llll}{\gamma }_{i1}& {\gamma }_{i2}& \cdots & {\gamma }_{ip}\end{array}\right]\left[\begin{array}{c}{b}_{j1}\\ b_{j2}\\ ⋮\\ b_{jp}\end{array}\right]\end{array}$$

则我们有如下的方程组

$$\left[\begin{array}{cccc}{\gamma }_{11}& {\gamma }_{12}& \cdots & {\gamma }_{1p}\\ {\gamma }_{21}& {\gamma }_{22}& \cdots & {\gamma }_{2p}\\ ⋮& ⋮& & ⋮\\ {\gamma }_{p1}& b_{p2}& \cdots & b_{pp}\end{array}\right]\left[\begin{array}{c}{b}_{j1}\\ b_{j2}\\ ⋮\\ b_{jp}\end{array}\right]=\left[\begin{array}{c}{a}_{1j}\\ a_{2j}\\ ⋮\\ a_{pj}\end{array}\right]$$

其中

$$\left[\begin{array}{cccc}{\gamma }_{11}& {\gamma }_{12}& \cdots & {\gamma }_{1p}\\ {\gamma }_{21}& {\gamma }_{22}& \cdots & {\gamma }_{2p}\\ ⋮& ⋮& & ⋮\\ {\gamma }_{p1}& b_{p2}& \cdots & b_{pp}\end{array}\right],\left[\begin{array}{c}{b}_{j1}\\ b_{j2}\\ ⋮\\ b_{jp}\end{array}\right],\left[\begin{array}{c}{a}_{1j}\\ a_{2j}\\ ⋮\\ a_{pj}\end{array}\right]$$

分别为原始变量的相关系数矩阵, 第 j 个因子得分函数的系数, 载荷矩阵的第 j 列。
用矩阵表示有

$$\left[\begin{array}{cccc}{b}_{11}& b_{21}& \cdots & b_{m1}\\ b_{12}& b_{22}& \cdots & b_{m2}\\ ⋮& ⋮& & ⋮\\ b_{1p}& b_{2p}& \cdots & b_{mp}\end{array}\right]=R^{-1}A$$

因此, 因子得分的估计为

$$\hat{F}={\left({\hat{F}}_{ij}\right)}_{n\times m}=X_0{R}^{-1}A$$

其中 ${\hat{F}}_{ij}$ 为第 $i$ 个样本点对第 $j$ 个因子 $F_j$ 得分的估计值, $X_0$ 是 $n\times m$ 的原始数据矩阵。

2. Bartlett 得分。一种估计因子得分系数的方法。所产生分数的平均值为 0 。使整个变量范围中所有唯一因子 的平方和达到最小。巴特莱特因子得分
   把 $x_i-{\mu }_i$ 看作因变量, 把因子载荷矩阵

$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1m}\\ a_{21}& a_{22}& \cdots & a_{2m}\\ ⋮& ⋮& & ⋮\\ a_{p1}& a_{p2}& \cdots & a_{pm}\end{array}\right]$$

看成自变量的观测。

$$\{\begin{array}{l}{x}_{i1}-{\mu }_1=a_{11}{f}_1+a_{12}{f}_2+\cdots +a_{1m}{f}_m+{\epsilon }_1\\ x_{i2}-{\mu }_2=a_{21}{f}_1+a_{22}{f}_2+\cdots +a_{2m}{f}_m+{\epsilon }_2\\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ x_{ip}-{\mu }_p=a_{p1}{f}_1+a_{p2}{f}_2+\cdots +a_{pm}{f}_m+{\epsilon }_p\end{array}$$

由于特殊因子的方差相异, 所以用加权最小二乘法求得分。使

$$\sum _{j=1}^p{\left[\left(x_{ij}-{\mu }_i\right)-\left(a_{i1}{\hat{f}}_1+a_{i2}{\hat{f}}_2+\cdots a_{im}{\hat{f}}_m\right)\right]}^2/{\sigma }_i^2$$

最小的 ${\hat{f}}_1,\cdots ,{\hat{f}}_m$ 是相应个案的因子得分。
用矩阵表达有

$$x-\mu =AF+\epsilon$$

则要使

$$(x-\mu -AF{)}^T{D}^{-1}(x-\mu -AF)$$

达到最小, 其中

$$D=\left[\begin{array}{lll}{\sigma }_1^2& & \\ & \ddots & \\ & & {\sigma }_p^2\end{array}\right]$$

使取得最小值的 $F$ 是相应个案的因子得分。
计算得 $F$ 满足

$$A^T{D}^{-1}F=A^T{D}^{-1}A(x-\mu )$$

解之得

$$\hat{F}={\left(A^T{D}^{-1}A\right)}^{-1}{A}^T{D}^{-1}(x-\mu )$$

3. Anderson-Rubin 方法 (Anderson-Rubin Method). 一种估计因子得分系数的方; 它对 Bartlett 方法做了修正, 从而确保被估计的因子的正交性。生成的分数平均值为 0 , 标准差为 1 , 且不相关。安德森一鲁宾因子得分法

九、数据检验

9.1 KMO检验

KMO检验是 Kaiser, Meyer和 Olkin提出的，该检验是对原始变量之间的简单相关系数和偏相关系数的相对大小进行验，主要应用于多元统计的因子分析。KMO统计量是取值在0和1之间，当所有变量间的简单相关系数平方和远远大于偏相关系数平方和时， KMO值越接近于1，意味着变量间的相关性越强，原有变量越适合作因子分析；当所有变量间的简单相关系数平方和接近0时， KMO值越接近于0,意味着变量间的相关性越弱，原有变量越不适合作因子分析。其中， Kaiser给出一个KMO检验标准： KMO>0.9,非常适合； 0.8

9.2 巴特利特球形检验

巴特利特球形检验是一种检验各个变量之间相关性程度的检验方法。一般在做因子分析之前都要进行巴特利特球形检验，用于判断变量是否适合用于做因子分析。巴特利特球形检验是以变量的相关系数矩阵为出发点的。它的原假设是相关系数矩阵是一个单位阵（不适合做因子分析，指标之间的相关性太差，不适合降维），即相关系数矩阵对角线上的所有元素都是1，所有非对角线上的元素都为0。巴特利特球形检验的统计量是根据相关系数矩阵的行列式得到的。如果该值较大，且其对应的p值小于用户心中的显著性水平（一般为0.05），那么应该拒绝原假设，认为相关系数不可能是单位阵，即原始变量之间存在相关性，适合于作因子分析。 相反不适合作因子分析。

9.3 碎石检验

碎石检验（scree test）是根据碎石图来决定因素数的方法。Kaiser提出，可通过直接观察特征值的变化来决定因素数。当某个特征值较前一特征值的值出现较大的下降，而这个特征值较小，其后面的特征值变化不大，说明添加相应于该特征值的因素只能增加很少的信息，所以前几个特征值就是应抽取的公共因子数。

碎石图得到的因子数只起到参考作用；在因子分析应用于某些专业问题上时，可能事先我们已经知道了最后要确定的因子数，这时候碎石图的意义就不大了。

十、应用

因子分析跟主成分分析一样，由于侧重点都是进行数据降维，因此很少单独使用，大多数情况下都会有一些模型组合使用。例如：

1. 因子分析（主成分分析）+多元回归分析：判断并解决共线性问题之后进行回归预测；
2. 因子分析（主成分分析）+聚类分析：通过降维后的数据进行聚类并分析数据特点，但因子分析会更适合，原因是基于因子的聚类结果更容易解释，而基于主成分的聚类结果很难解释；
3. 因子分析（主成分分析）+分类：数据降维（或数据压缩）后进行分类预测，这也是常用的组合方法。

十一、实现步骤流程及示例分析

流程：

1. 相关性检验，一般采用KMO检验法和Bartlett球形检验法两种方法来对原始变量进行相关性检验；
2. 输入原始数据$X_{n\ast p}$，计算样本均值和方差，对数据样本进行标准化处理；
3. 计算样本的相关矩阵$R$；
4. 求相关矩阵R的特征根和特征向量；
5. 根据系统要求的累积贡献率确定公共因子的个数；
6. 计算因子载荷矩阵$A$；
7. 对载荷矩阵进行旋转，以求能更好地解释公共因子；
8. 确定因子模型；
9. 根据上述计算结果，求因子得分，对系统进行分析

示例：
假设某一社会经济系统问题, 其主要特性可用 4 个指标表示, 它们分别是生产、技术、交通和环境。其相关矩阵为:

$$R=\left[\begin{array}{cccc}1& 0.64& 0.29& 0.1\\ 0.64& 1& 0.7& 0.3\\ 0.29& 0.7& 1& 0.84\\ 0.1& 0.3& 0.84& 1\end{array}\right]$$

相应的特征值、占总体百分比和累计百分比如下表:

对应特征值的特征向量矩阵为:

$$U=\left[\begin{array}{cccc}0.38& 0.67& 0.62& -0.14\\ 0.54& 0.36& -0.61& 0.46\\ 0.59& -0.3& -0.2& -0.72\\ 0.47& -0.58& 0.45& 0.50\end{array}\right]$$

假吅要求所取特征值反映的信息量占总体信息量的 90 % 以上，则从男计徍征值所占百分比看，只需取前两项即可。也就是说，只需取两个 主要因子。对应于前两列特征值的特征向量, 可求的其因子载荷矩阵A为:

$$A=\left[\begin{array}{cc}0.60& 0.71\\ 0.85& 0.38\\ 0.93& -0.32\\ 0.74& -0.40\end{array}\right]$$

于是，该问题的因子模型为:

$$\begin{array}{l}{x}_l=0.60f_1+0.71f_2\\ x_2=0.85f_1+0.38f_2\\ x_3=0.93f_1-0.32f_2\\ x_4=0.74f_1-0.40f_2\end{array}$$
因子分析：由以上可以看出，两个因子中，$f_1$是全面反映生产、技术、交通和环境的因子，而$f_2$却不同，它反映了对生产和技术这两项增长有利，而对交通和环境增长不利的因子。也就是说，按照原有统计资料得出的相关矩阵分析的结果是如果生产和技术都随$f_2$增长了，将有可能出现交通紧张和环境恶化的问题，$f_2$反映了这两方面的相互制约状况。

十二、python实现因子分析

数据集：

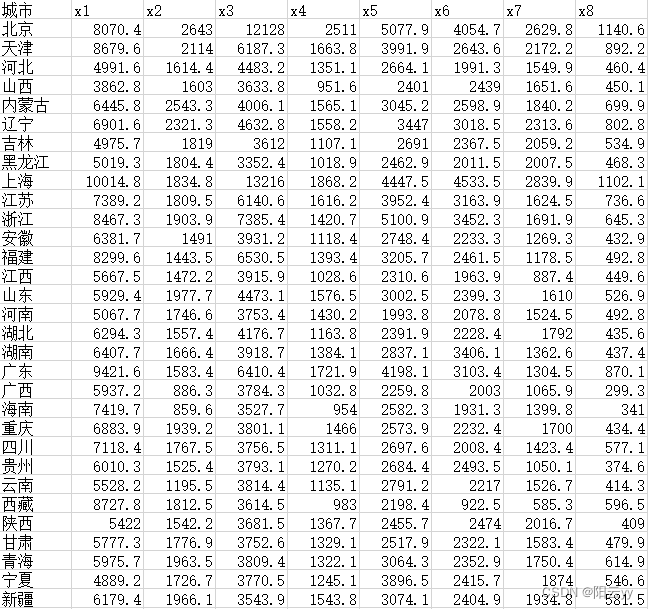
列名使用中文会报错，未解决。采用x(1-8)代替不影响结果。

1. 导入库

# 数据处理
import pandas as pd
import numpy as np
# 绘图
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib as mpl
# 因子分析
from factor_analyzer import FactorAnalyzer
# Bartlett's球状检验
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
#KMO检验
from factor_analyzer.factor_analyzer import calculate_kmo

2. 导入数据，去掉城市一列

df = pd.read_excel("data_1.xls",index_col=0).reset_index(drop=True)
print(df)
print(df.isnull().sum())

3. 数据检验

# Bartlett's球状检验
# 检验总体变量的相关矩阵是否是单位阵（相关系数矩阵对角线的所有元素均为1,所有非对角线上的元素均为零）；即检验各个变量是否各自独立。
# 如果不是单位矩阵，说明原变量之间存在相关性，可以进行因子分子；反之，原变量之间不存在相关性，数据不适合进行主成分分析
chi_square_value, p_value = calculate_bartlett_sphericity(df)
print("Bartlett's球状检验参数：\n",chi_square_value, p_value)
#KMO检验
# 检查变量间的相关性和偏相关性，取值在0-1之间；KOM统计量越接近1，变量间的相关性越强，偏相关性越弱，因子分析的效果越好。
# 通常取值从0.6开始进行因子分析
kmo_all,kmo_model=calculate_kmo(df)
print("KMO检验参数：\n",kmo_model)

4. 选择因子个数

# 构建因子分析模型
fa = FactorAnalyzer(8, rotation=None)
# 训练模型
fa.fit(df)

# 得到特征值ev、特征向量v
ev, v = fa.get_eigenvalues()
print(ev, v)

# 同样的数据绘制散点图和折线图
plt.scatter(range(1, df.shape[1] + 1), ev)
plt.plot(range(1, df.shape[1] + 1), ev)

# 显示图的标题和xy轴的名字
# 最好使用英文，中文可能乱码
plt.title("Scree Plot")
plt.xlabel("Factors")
plt.ylabel("Eigenvalue")


mpl.rcParams['font.sans-serif'] = ['SimHei']  # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
plt.grid()  # 显示网格
plt.show()  # 显示图形

5. 因子旋转

# 选择方式： varimax 方差最大化
# 选择固定因子为2个
fa_two = FactorAnalyzer(2,rotation='varimax')
fa_two.fit(df)
# 查看每个变量的公因子方差数据
pd.DataFrame(fa_two.get_communalities(),index=df.columns)
# 查看旋转后的特征值
pd.DataFrame(fa_two.get_eigenvalues())
# 查看成分矩阵
# 变量个数*因子个数
pd.DataFrame(fa_two.loadings_,index=df.columns)
# 查看因子贡献率
fa_two.get_factor_variance()
# 隐藏变量可视化
df1 = pd.DataFrame(np.abs(fa_two.loadings_),index=df.columns)
print(df1)

# 绘图

plt.figure(figsize=(14, 14))
ax = sns.heatmap(df1, annot=True, cmap="BuPu")

# 设置y轴字体大小
ax.yaxis.set_tick_params(labelsize=15)
plt.title("Factor Analysis", fontsize="xx-large")

# 设置y轴标签
plt.ylabel("Sepal Width", fontsize="xx-large")
# 显示图片
plt.show()

# 保存图片
# plt.savefig("factorAnalysis", dpi=500)

6. 因子分析新变量

# 转换新变量
df2 = pd.DataFrame(fa_two.transform(df))
print(df2)

碎石图：

系数矩阵：